preface

I've been dragged to the bride in the last two days and haven't done anything. So let's start with a few simple questions to find self-confidence (dog head)

subject

Arithmetic square

Give you a nonnegative integer x, calculate and return the arithmetic square root of X.

Since the return type is an integer, only the integer part will be retained and the decimal part will be rounded off.

Note: it is not allowed to use any built-in exponential functions and operators, such as pow(x, 0.5) or x ** 0.5.

Example 1:

Input: x = 4 Output: 2 example 2:

Input: x = 8 output: 2 explanation: the arithmetic square root of 8 is 2.82842... Because the return type is an integer, the decimal part will be rounded off

I was scared when I looked at this topic. Meow didn't let me use it. After thinking for a long time, I couldn't do anything else. Later, I checked and found that meow had a simplified calculation formula.
This solution is the simplest.

e2lnx = x2

Therefore, the first method is to directly set a set of formulas

class Solution {
    public int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }
        int ans = (int) Math.exp(0.5 * Math.log(x));
        return (long) (ans + 1) * (ans + 1) <= x ? ans + 1 : ans;
    }
}

The second method is dichotomy. Is to guess the range of this number. This code is also easy to understand

class Solution {
    public int mySqrt(int x) {
        int left = 0, right = x, ans = -1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if ((long) mid * mid <= x) {
                ans = mid;
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return ans;
    }
}

climb stairs

This topic is a classic topic of dynamic programming. At the same time, it is also an application of Fibonacci numbers. When I first learned python, I remember that I always liked the Fibonacci sequence and the eight queens problem in the book. Now think about why I didn't brush the algorithm well from that time.

subject

Suppose you are climbing stairs. You need n steps to reach the roof.

You can climb one or two steps at a time. How many different ways can you climb to the roof?

Note: given n is a positive integer.

Example 1:

Input: 2 output: 2 explanation: there are two ways to climb to the roof.
1st order + 1st order
Second order example 2:

Input: 3 output: 3 explanation: there are three ways to climb to the roof.
1st order + 1st order + 1st order
1st order + 2nd order
2nd order + 1st order

The idea is actually very simple. Think for yourself. Suppose I want to go to the fifth staircase, can I come directly from the fourth and third stairs? Then there are several ways to get to the third and fourth stairs. The sum of the two is the way of the fifth. At the same time, the third and fourth come from there, so we can draw a conclusion, There are 0 walking methods starting from 0. There is one way to reach the first one. The second can come from the first one or from the 0, that is, 0 + 1, 1, and so on

0 1 1 2 3 5... This is just a sequence. There are several ways to write this sequence and several solutions to this problem.

Here's the simplest one.

class Solution {
    public int climbStairs(int n) {
        int p = 0, q = 0, r = 1;
        for (int i = 1; i <= n; ++i) {
            p = q; 
            q = r; 
            r = p + q;
        }
        return r;
    }
}

What we are talking about here is that the topic of dynamic programming has a typical feature, that is, we can get an equation of state, that is, the current operation must be obtained from the previous step or several parts, which will be affected by the above, that is, we can get an equation of state
F(n) = F(n-m)+F(n-k),m,k are steps, and we can get the initial state at the beginning, that is, the initial iterative state

This type of problem is very similar to the thinking mode of the big problem of what proportional sequence in that high school.

Now that we have talked about this, let's talk about some topics related to dynamic programming.

Yang Hui triangle

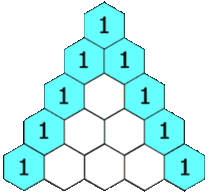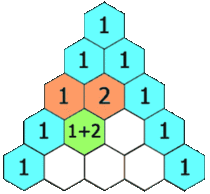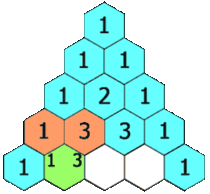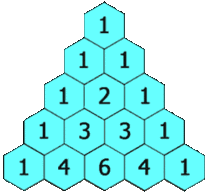
Let's talk about the characteristics first. Look carefully, the outermost layer is 1, and the first and second layers are 1, that is, the initial state
The numbers in the middle are affected by the above two, so we can build equations, so we don't run dynamic programming, and we know the state equation and initial state, so it's not easy to find the one at the next level.

Input: numRows = 5 Output: [[1], [1,1], [1,2,1], [1,3,3,1], [1,4,6,4,1]]

Here we use a two-dimensional array to store, and then it's OK. The java version is a little ugly. Here are the java and python versions

class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> YanghuiSanJiao = new ArrayList<List<Integer>>();
        for (int i = 0; i < numRows; i++) {
            List<Integer> row = new ArrayList<Integer>();
            for (int j = 0; j <= i; ++j) {
                if (j == 0 || j == i) {
                    row.add(1);
                } else {
                    row.add(YanghuiSanJiao.get(i - 1).get(j - 1) + YanghuiSanJiao.get(i - 1).get(j));
                }
            }
            YanghuiSanJiao.add(row);
        }
        return YanghuiSanJiao;
    }
}

python

class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        YanghuiSanJiao = list()
        for i in range(numRows):
            row = list()
            for j in range(0, i + 1):
                if j == 0 or j == i:
                    row.append(1)
                else:
                    row.append(YanghuiSanJiao[i - 1][j] + YanghuiSanJiao[i - 1][j - 1])
            YanghuiSanJiao.append(row)
        return YanghuiSanJiao

Yanghui triangle 2

This is a small deformation

Given a nonnegative index rowIndex, return the rowIndex row of "Yang Hui triangle".

In the Yang Hui triangle, each number is the sum of its upper left and upper right numbers.

Example 1:

Input: rowIndex = 3 output: [1,3,3,1]

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<List<Integer>> YanghuiSanJiao = new ArrayList<List<Integer>>();
        for (int i = 0; i <= rowIndex; ++i) {
            List<Integer> row = new ArrayList<Integer>();
            for (int j = 0; j <= i; ++j) {
                if (j == 0 || j == i) {
                    row.add(1);
                } else {
                    row.add(YanghuiSanJiao.get(i - 1).get(j - 1) + YanghuiSanJiao.get(i - 1).get(j));
                }
            }
            YanghuiSanJiao.add(row);
        }
        return YanghuiSanJiao.get(rowIndex);
    }
}

Different paths

A robot is located in the upper left corner of an m x n grid (the starting point is marked "Start" in the following figure).

The robot can only move down or right one step at a time. The robot attempts to reach the lower right corner of the grid (marked "Finish" in the following image).

How many different paths are there altogether?
Input: m = 3, n = 7
Output: 28
Example 2:

Input: m = 3, n = 2, output: 3

This is the same.

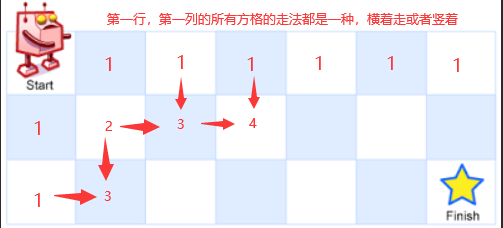
Directly to the code.

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] f = new int[m][n];
        for (int i = 0; i < m; ++i) {
            f[i][0] = 1;
        }
        for (int j = 0; j < n; ++j) {
            f[0][j] = 1;
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                f[i][j] = f[i - 1][j] + f[i][j - 1];
            }
        }
        return f[m - 1][n - 1];
    }
}

Play here, the relatively simple dynamic programming is basically like this.