⭐ New pit in winter vacation -- daily question notes of code Fox

1220. Count the number of vowel sequences - Hard

Title Description:

Give you an integer n, please help us count how many strings with length n can be formed according to the following rules:

• Each character in the string should be a lowercase vowel ('a ',' e ',' I ',' o ',' U ')
• Each vowel 'a' can only be followed by 'e'
• Each vowel 'e' can only be followed by 'a' or 'i'
• Each vowel 'i' cannot be followed by another 'i'
• Each vowel 'o' can only be followed by 'i' or 'u'
• Each vowel 'u' can only be followed by 'a'

Since the answer may be very large, please return the result after module 10 ^ 9 + 7.

Problem solving method:

A very basic dynamic programming method. If the state is the possible combination number of characters ending with the current letter, such as the combination ending with a with length 2, ea, ia and ua, then dp[2] [a] = 3; Since there is no need to save the intermediate state, it is directly written as DP ['a '] = 3 - it can be seen from the meaning of the question that the end of a with length 2 can be composed of E, I and u with length 1 and added with a. the existing DP ['a'] = pre_dp[‘e’]+pre_dp[‘i’]+pre_dp[‘u’]

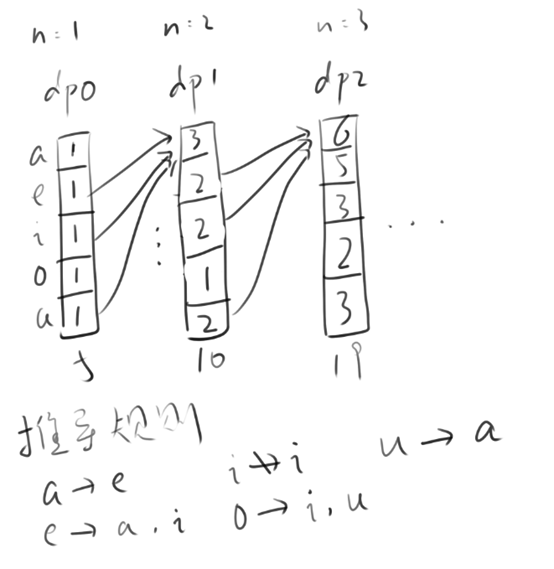
Code implementation:

class Solution {
    public final static int MOD=1000000000+7;
    
    public int countVowelPermutation(int n) {
        //state
        int[] ans=new int[5];
        //Pre state
        int[] mid=new int[5]; 
        
        //dp initialization
        for(int i=0;i<5;i++){
            ans[i]=1;
        }
        n-=1;
        
        while(n-->0){
            //dp derivation rule, which deduces the next state from the previous dp state
            mid[0]=((ans[1]+ans[2])%MOD+ans[4])%MOD;
            mid[1]=(ans[0]+ans[2])%MOD;
            mid[2]=(ans[1]+ans[3])%MOD;
            mid[3]=ans[2];
            mid[4]=(ans[2]+ans[3])%MOD;
            
            for(int i=0;i<5;i++){
                ans[i]=mid[i];
            }
        }
        //The result is the sum of five possible endings of length n
        int ans_=0;
        for(int i=0;i<5;i++){
            ans_=(ans[i]+ans_)%MOD;
        }
        return ans_;
    }
}

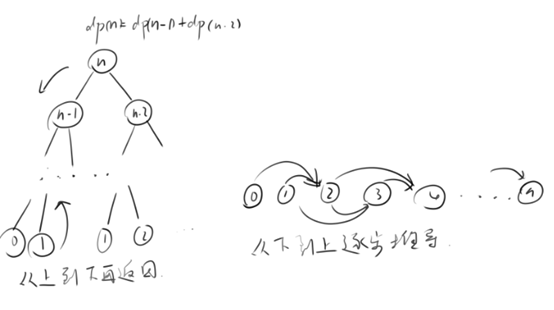
Dynamic programming (DP)

• Practical problems: in real life, there is a kind of activity process. Due to its particularity, the process can be divided into several interrelated stages. In each stage, decisions need to be made to make the whole process achieve the best activity effect (for example:
• Multi-stage decision-making: when the decisions of each stage are determined, a decision sequence is formed, so an activity route of the whole process is determined. This kind of multi-stage decision-making process that regards a problem as a multi-stage process with chain structure is called multi-stage decision-making process, and this kind of problem is called multi-stage decision-making problem
• Dynamic programming: in the multi-stage decision-making problem, the decision taken in each stage is generally time-dependent. The decision depends on the current state and then leads to the transfer of the state. A decision sequence is generated in the changing state, so it has the meaning of "dynamic". This process of solving the optimization of multi-stage decision-making is called dynamic programming method

The multi-stage problems that meet the above description can be solved by dynamic programming steps - the bottom-up process can be solved by iterative derivation, and the top-down process can be solved by recursion

322. Change Mid

Title Description

Give you an integer array of coins to represent coins of different denominations; And an integer amount representing the total amount.

Calculate and return the minimum number of coins required to make up the total amount. If no coin combination can make up the total amount, return - 1.

You can think that the number of each coin is unlimited.

Problem solving method

Since the amount of a certain quantity can be obtained by the combination of the previous amount and the corresponding Coin - set the status array as the amount quantity I - dp[i]=min(dp[i-coins[index]]+1); The minimum combination can be obtained by judgment, and the local dp optimization deduces the global optimization

Code implementation:

class Solution {
    public int coinChange(int[] coins, int amount) {
        //If the number of change required is 0, no coin is required
        if(amount==0)
            return 0;
        
        int coins_l=coins.length;
        int[] dp=new int[amount+1];
        
        for(int i=0;i<=amount;i++){
            for(int c=0;c<coins_l;c++){
                //Derivation process - dp[i]=min(i-coins[0:coins_l-1])
                int mid=i-coins[c];
                //It just consists of a coin
                if(mid==0){
                    dp[i]=1;
                }
                //The derivation process prevents the array from crossing the boundary. It cannot be combined and represented by 0 (it can be represented by maximum value)
                if(mid>0&&dp[mid]!=0&&(dp[i]>dp[mid]+1||dp[i]==0)){
                    dp[i]=dp[mid]+1;
                }
                
            }
        }
        //Output results
        if(dp[amount]==0){
            return -1;
        }
        else{
            return dp[amount];
        }
    }
}

ending

Title Source: LeetCode link: https://leetcode-cn.com/problems

⭐ Pay attention to the author, take you to brush the questions, and learn the most commonly used algorithm skills from simple algorithm questions (one question every day in winter vacation)
⭐ Pay attention to the author's problem brushing - simple to advanced, which makes you unknowingly become a ruthless problem brushing machine. Please send a private letter if you have any questions