Title Description

Give you an integer matrix isWater with the size of m x n, which represents a map composed of land and water cells.

• If i s W a t e r [ i ] [ j ] = = 0 isWater[i][j] == 0 isWater[i][j]==0, grid ( i , j ) (i, j) (i,j) is a land grid.
• If i s W a t e r [ i ] [ j ] = = 1 isWater[i][j] == 1 isWater[i][j]==1, grid ( i , j ) (i, j) (i,j) is a water grid.

You need to arrange the height of each cell according to the following rules:

• The height of each lattice must be nonnegative.
• If a grid is a water area, its height must be 0.
• The height difference of any adjacent grid is at most 1. When two grids are close to each other in due east, South, West and North, they are called adjacent grids (that is, they have a common edge).

Find a scheme to arrange the height so that the highest height value in the matrix is the largest.

Please return an integer matrix height of size m x n, where h e i g h t [ i ] [ j ] height[i][j] height[i][j] is the height of the lattice (i, j). If there are multiple solutions, please return any one.

Example 1

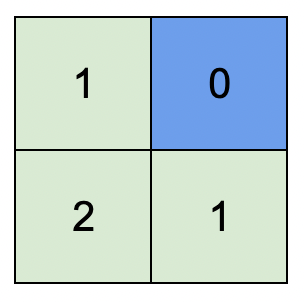
Input: isWater = [[0,1],[0,0]]
Output:[[1,0],[2,1]]
Explanation: the figure above shows the height of each grid.
The blue grid is the water grid and the green grid is the land grid.

Example 2

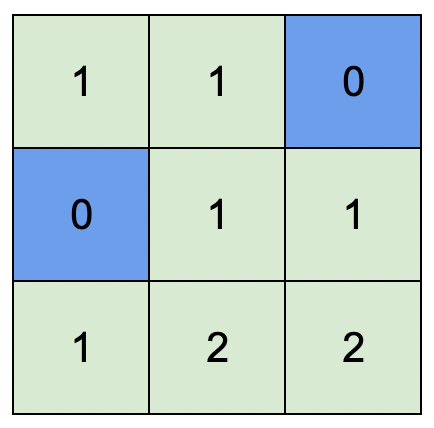
Input: isWater = [[0,0,1],[1,0,0],[0,0,0]]
Output:[[1,1,0],[0,1,1],[1,2,2]]
Explanation: among all arrangements, the maximum feasible height is 2.
In any arrangement scheme, as long as the maximum height is 2 and meets the above rules, it is a feasible scheme.

Tips

• m = = i s W a t e r . l e n g t h m == isWater.length m==isWater.length
• n = = i s W a t e r [ i ] . l e n g t h n == isWater[i].length n==isWater[i].length
• 1 < = m , n < = 1000 1 <= m, n <= 1000 1<=m,n<=1000
• i s W a t e r [ i ] [ j ] isWater[i][j] isWater[i][j] is either 0 or 1.
• At least 1 water grid.

Problem solving ideas

The first thought is to create an empty matrix height with the same size as the grid, and then fill it gradually according to the law described in the topic. For the grid with 1 in the map, fill the corresponding position of height as 0, and then traverse the height matrix step by step. According to the requirements described in the topic:

• Fill the grid around 0 with 1
• Fill the grid of 1 with 2
• ...
• Until there is no free space

Note: the height difference shall be at most 1 during filling.
The code is as follows:

class Solution:
    # Algorithm timeout
    def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:
        m = len(isWater)
        n = len(isWater[0])
        height = [[-2 for i in range(n)] for j in range(m)]
        negCount = m * n
        index = 0
        for i in range(m):
            for j in range(n):
                if isWater[i][j] == 1:
                    height[i][j] = index
                    negCount -= 1
        while negCount > 0:
            for i in range(m):
                for j in range(n):
                    if height[i][j] == index:
                        if i + 1 < m and abs(height[i + 1][j] - height[i][j]) > 1:
                            height[i + 1][j] = index + 1
                            negCount -= 1
                        if i - 1 >= 0 and abs(height[i - 1][j] - height[i][j]) > 1:
                            height[i - 1][j] = index + 1
                            negCount -= 1
                        if j + 1 < n and abs(height[i][j + 1] - height[i][j]) > 1:
                            height[i][j + 1] = index + 1
                            negCount -= 1
                        if j - 1 >= 0 and abs(height[i][j - 1] - height[i][j]) > 1:
                            height[i][j - 1] = index + 1
                            negCount -= 1
            index += 1
        return height

Obviously, the time complexity of the algorithm is too high. Once there is an unfilled lattice, the whole matrix height must be traversed again. Therefore, we consider using queues to record the location of elements.

Since the height difference of any adjacent grid is at most 1, this means that for each grid, its height is at most 1 higher than the minimum height in its adjacent grid. The title requires that the height of the water area must be 0, so the height of the water area is a determined value. We can deduce the height of other grids from the water area:

• First, calculate the height of the grid adjacent to the water area. For these grids, the minimum height in their adjacent grids is the height of the water area 0, so the height of these grids is 1.
• Then, the height of the lattice adjacent to the lattice with height 1 and not yet calculated is calculated. For these lattices, the minimum height of their adjacent lattices is 1, so the height of these lattices is 2.
• By analogy, calculate the height of all grids.

In the above process, for each round, we consider the uncomputed grid x adjacent to the grid of the previous round, and its height must be 1 higher than that of the previous round. It can be found that the above process is the process of breadth first search starting from the water area. Therefore, the answer is to record the location of all water areas, and then perform breadth first search to calculate the height of all land grids.
The code is as follows:

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# @FileName  :HighestPeak.py
# @Time      :2022/1/29 21:29
# @Author    :PangXZ
# Leetcode: the highest point in 1765 map
from collections import deque
from typing import List


class Solution:
    # Multi source breadth first search
    def highestPeak2(self, isWater: List[List[int]]) -> List[List[int]]:
        m, n = len(isWater), len(isWater[0])
        height = [[water - 1 for water in row] for row in isWater]  # The water area is 0 and the unfilled position is - 1
        q = deque((i, j) for i, row in enumerate(isWater) for j, water in enumerate(row) if water)  # Team up all waters
        while q:
            i, j = q.popleft()
            for x, y in ((i - 1, j), (i + 1, j), (i, j - 1), (i, j + 1)):
                if 0 <= x < m and 0 <= y < n and height[x][y] == -1:
                    height[x][y] = height[i][j] + 1
                    q.append((x, y))
        return height


if __name__ == "__main__":
    isWater = [[0, 0, 1], [1, 0, 0], [0, 0, 0]]
    solution = Solution()
    print(solution.highestPeak2(isWater))

Complexity analysis

• Time complexity: O(mn)
• Spatial complexity: O(mn). In the fastest case, the whole matrix is water area, and all water areas need to be included in the team.