Recursion from introduction to mastery

(I) introduction to recursion

Write a recursive function

• What is the function of this recursive function and how to call this function, that is, design the return value and parameter list of the recursive function
• When should this recursion end and what is its boundary condition (exit)
• How to change from the nth layer to the n+1 layer in the non boundary case (recursive formula)

1.1 recursive factorial calculation

n ! = { 1 n = 0 n ∗ ( n − 1 ) ! n > 0 n!=\begin{cases} 1 & n=0 \\ n*(n-1)! & n>0 \end{cases} n!={1n∗(n−1)!​n=0n>0​

#include <stdio.h>

int fact(int n) {
    if (n == 0) return 1;//boundary
        return n * fact(n - 1);//formula
}

int main() {
    int ans = fact(10); //call
    printf("%d\n", ans);
    return 0;
}

1.2. Recursive computation Fibonacci sequence (fib)

Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ......
f ( n ) = { 0 n = 0 1 n = 1 f ( n − 2 ) + f ( n − 1 ) n > 1 f(n)=\begin{cases} 0 & n=0 \\ 1 & n=1 \\ f(n-2)+f(n-1) & n>1 \end{cases} f(n)=⎩⎪⎨⎪⎧​01f(n−2)+f(n−1)​n=0n=1n>1​

#include <stdio.h>

int fib(int n) {
	if (n == 0) return 0;
	if (n == 1) return 1;
	return fib(n - 1) + fib(n - 2);
}

int main() {
	for (int i = 0;i < 10;i++) {
		printf("%d ", fib(i));
	}
	printf("\n");
	return 0;
}

1.3. Recursive computing greatest common divisor

gcd(12, 32) = 4

gcd(a,   b)
gcd(32,  12)
gcd(12,  8)
gcd(8,   4)
gcd(4,   0)

g c d ( a , b ) = { a b = 0 g c d ( b , a % b ) b ≠ 0 gcd(a,b)=\begin{cases} a & b=0 \\ gcd(b,a \% b) & b\neq 0 \end{cases} gcd(a,b)={agcd(b,a%b)​b=0b​=0​

//Rolling Division
#include <stdio.h>
int gcd(int a, int b) {
	if (b == 0)return a;
	return gcd(b, a % b);
}

int main() {
	printf("%d ", gcd(12, 32));
}

Divide and conquer algorithm

Design idea of divide and conquer method:

1. Score – decompose the problem into smaller subproblems;
2. Governance – break down these smaller sub problems one by one;
3. Combination – merge the solved sub problems to finally obtain the solution of the "parent" problem;

• Reduce and cure (reduce the scale of the problem by 1 each time)
• Divide and rule (halve the scale of the problem each time) (the idea of merging and sorting)

1.4 recursive total stair jumping method (reduce and cure - reduce the problem scale by one)

Title Description:
One step has a total of n Level. If you can skip level 1 at a time, you can also skip Level 2. Find the total number of jumps.
First line input T，Indicates how many test data there are. next T Line, enter a number for each line n，Represents the order of the step.
When outputting, each line corresponds to one output.

Sample input:
3
5
8
10

Sample output:
8
34
89

Resolution:

f ( n ) = { 1 n = 1 2 n = 2 f ( n − 1 ) + f ( n − 2 ) n > 2 f(n)=\begin{cases} 1 & n=1 \\ 2 & n=2 \\ f(n-1)+f(n-2) & n>2 \end{cases} f(n)=⎩⎪⎨⎪⎧​12f(n−1)+f(n−2)​n=1n=2n>2​

Reference code:

#include <stdio.h>

int solve(int n) {
	if (n == 1) return 1;
	if (n == 2) return 2;
	//Such as: solve(5)
	//From 1 to > 2 levels: that is, the strategy of "jump one level" is adopted first, and the total jump method of the next four steps is solve(4)
	//From 1 to > 3 levels: that is, the strategy of "jumping two levels" is adopted first, and the total jumping method of the next three steps is solve(3)
	return solve(n - 1) + solve(n - 2);
}

int main() {

	//int T;
	//scanf_ s("%d", &T);// Set the number of tests
	//while (T--) {
	//	int n;
	//	scanf_ s("%d", &n);// Set the number of steps
	int ans = solve(5);
	printf("%d\n", ans);
	return 0;
}

1.5 recursive ranking problem (divide and Conquer - problem scale halved)

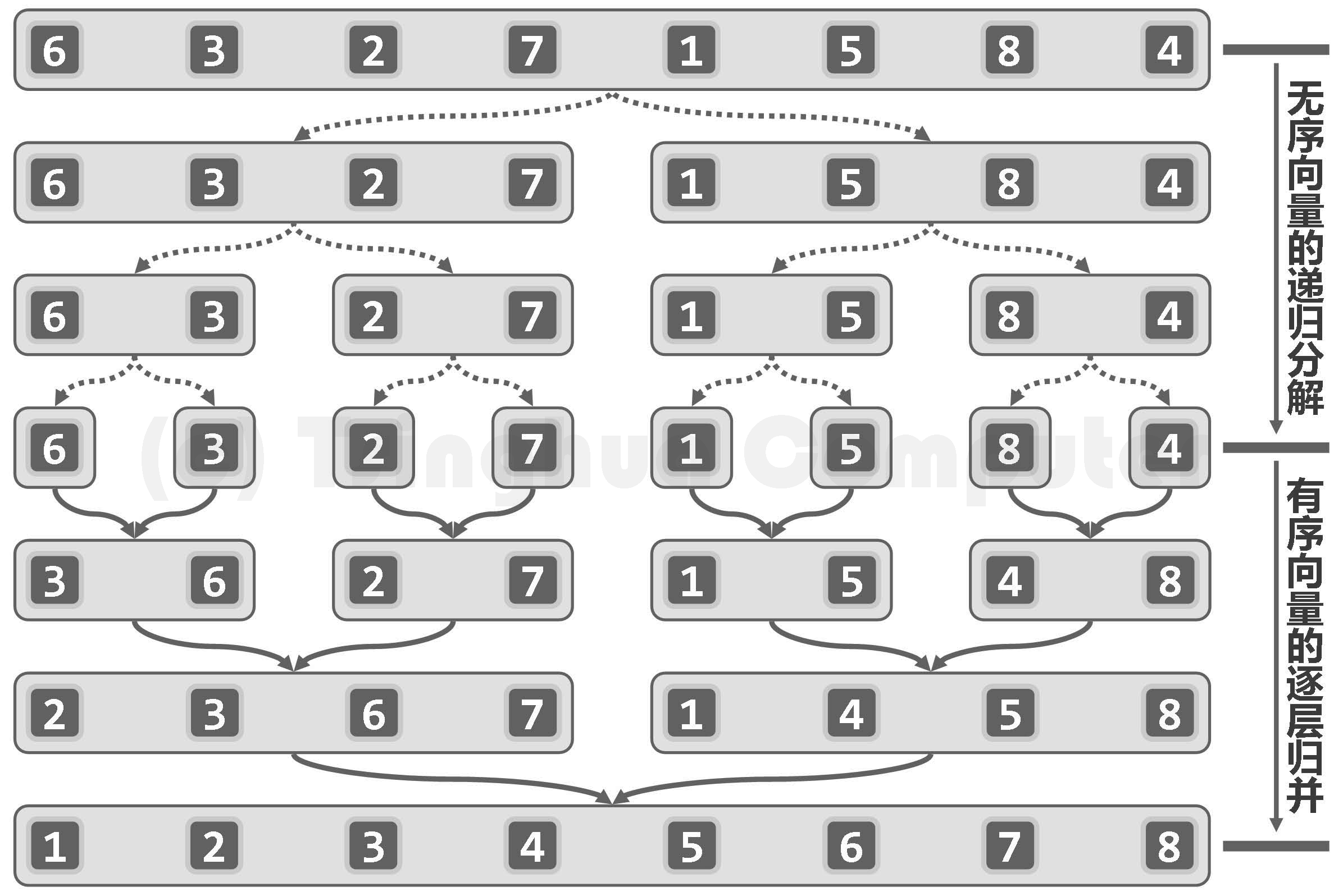
#include   <iostream>
using  namespace std;


void mergeArray(int A[], int l, int mid, int r) {
	int* temp = new int[r - l + 1];
	int i = l, j = mid + 1;//i points to the first index of the 'first half' and j points to the first index of the 'second half'
	int k = 0;//Temporary temp [] header index

	//Assign 'A [] first half' to temporary temp []
	while (i <= mid && j <= r) {
		if (A[i] <= A[j])temp[k++] = A[i++];
		else temp[k++] = A[j++];
	}
	//Assign 'the second half of A [] to temporary temp []
	while(j <= r)temp[k++] = A[j++];
	while (i <= mid)temp[k++] = A[i++];

	//Assign A [] to temp [] temporarily so that A [] can be truly sorted
	
	for (int i = l, k = 0;i <= r;i++, k++) {
		A[i] = temp[k];
	}
	delete temp;
}



//Merge sort
void mergesort(int A[], int l, int r) {
	if (l >= r) return;
	int mid = l + (r - l) / 2;
	mergesort(A, l, mid);Left half interval[lo, mid] Order
	mergesort(A, mid+1, r);Right half interval[mid + 1, hi] Order
	mergeArray(A, l, mid, r);//Merge
}


int main() {
	int A[] = { 6,1,2,9,7,3 };
	int N = sizeof(A) / sizeof(int);

	mergesort(A, 0, N - 1);
	for (int x : A) {
		cout << x << " ";
	}
	cout << endl;
	return 0;
}

(II) binary tree, tree

Traversal of binary tree

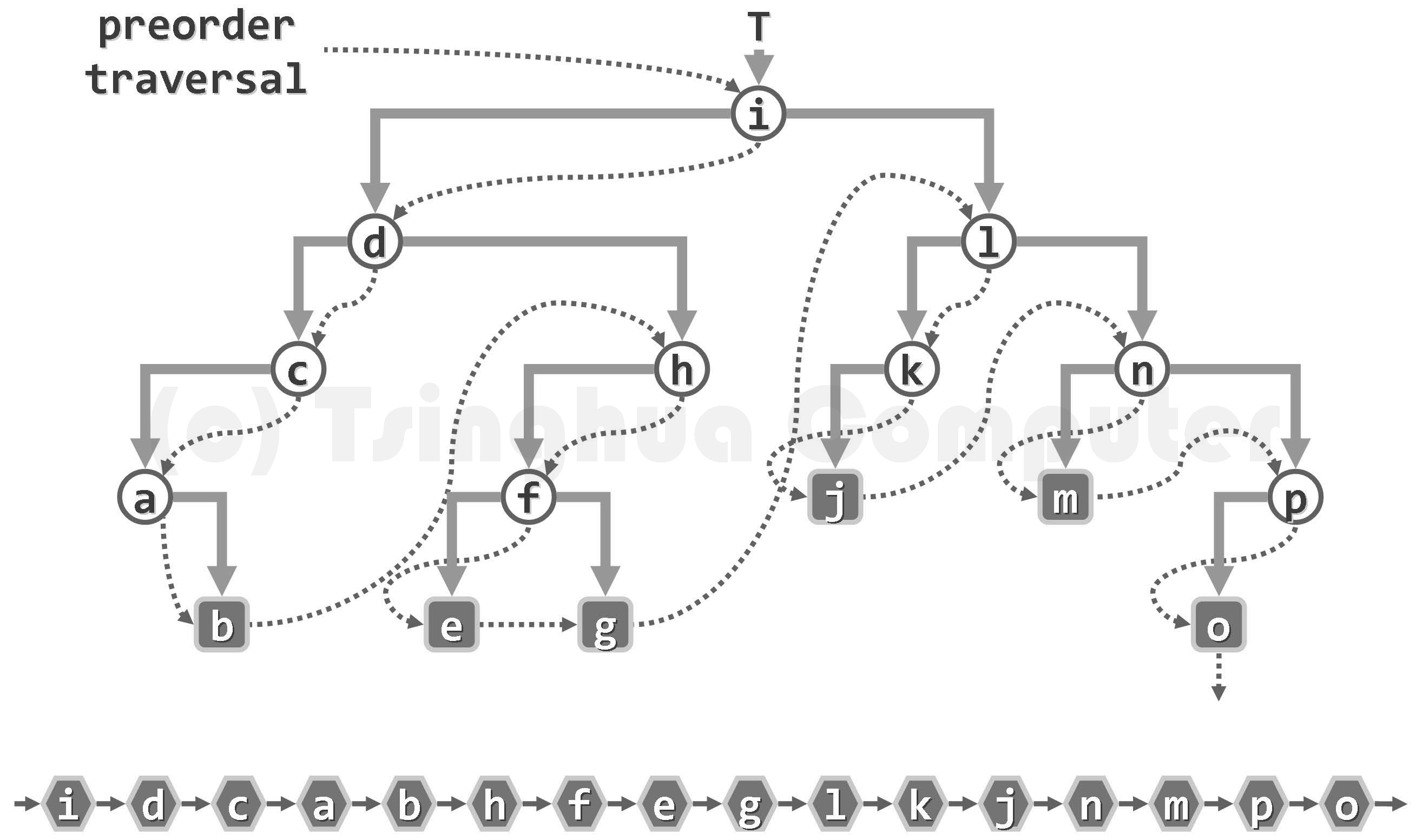
Preorder traversal

Middle order traversal

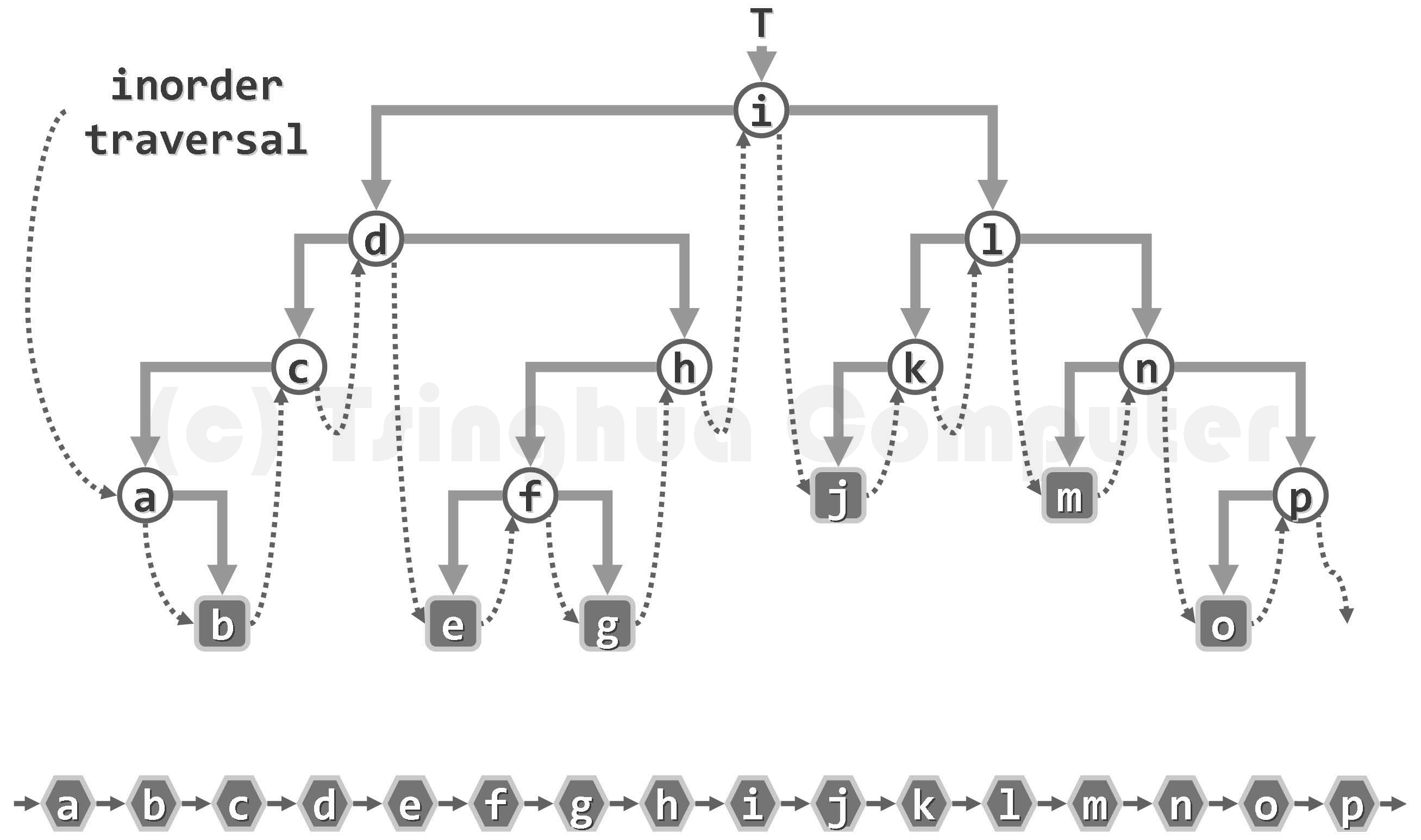
The projection order of binary tree nodes in the horizontal direction is the middle order traversal order.

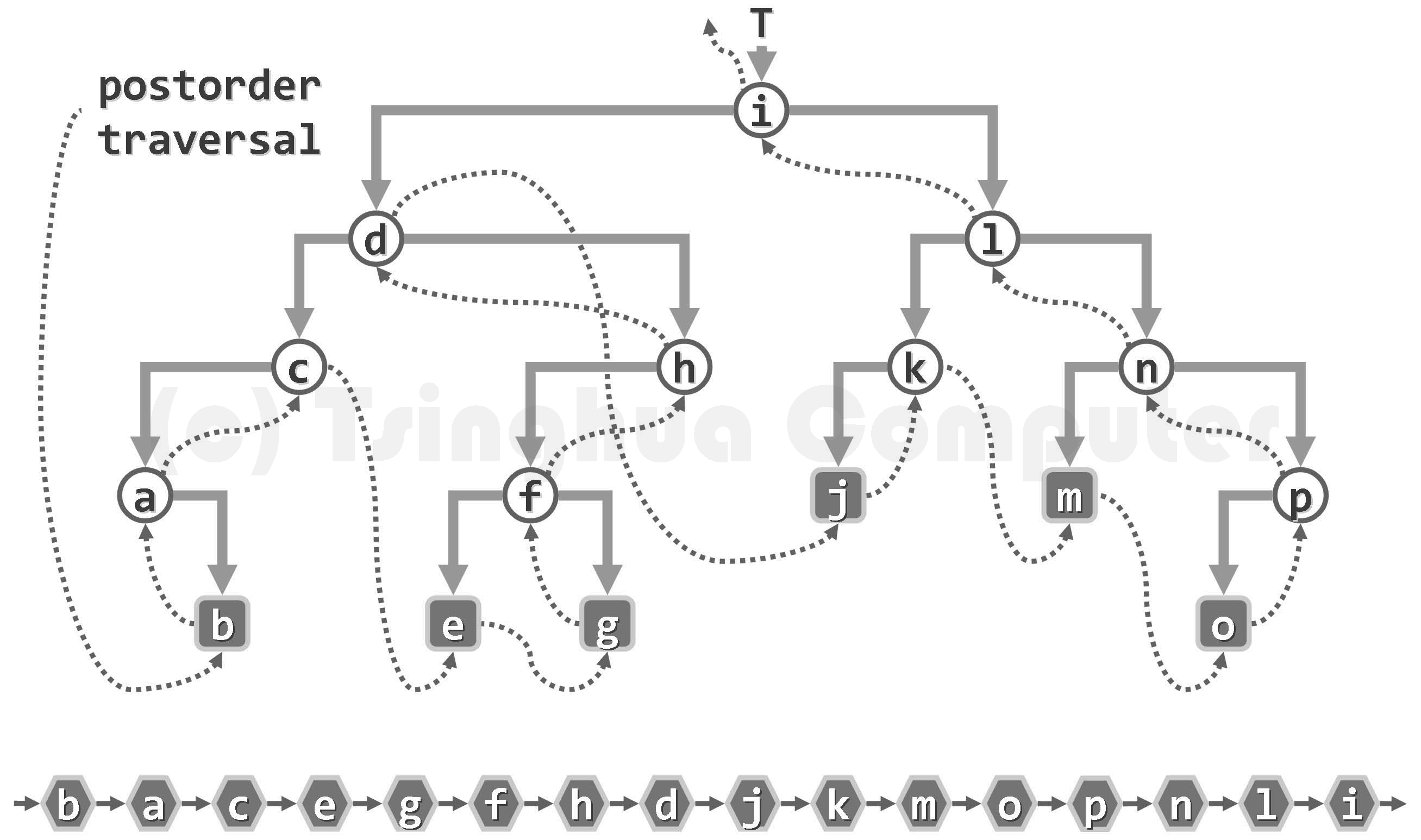
Postorder traversal

level traversal

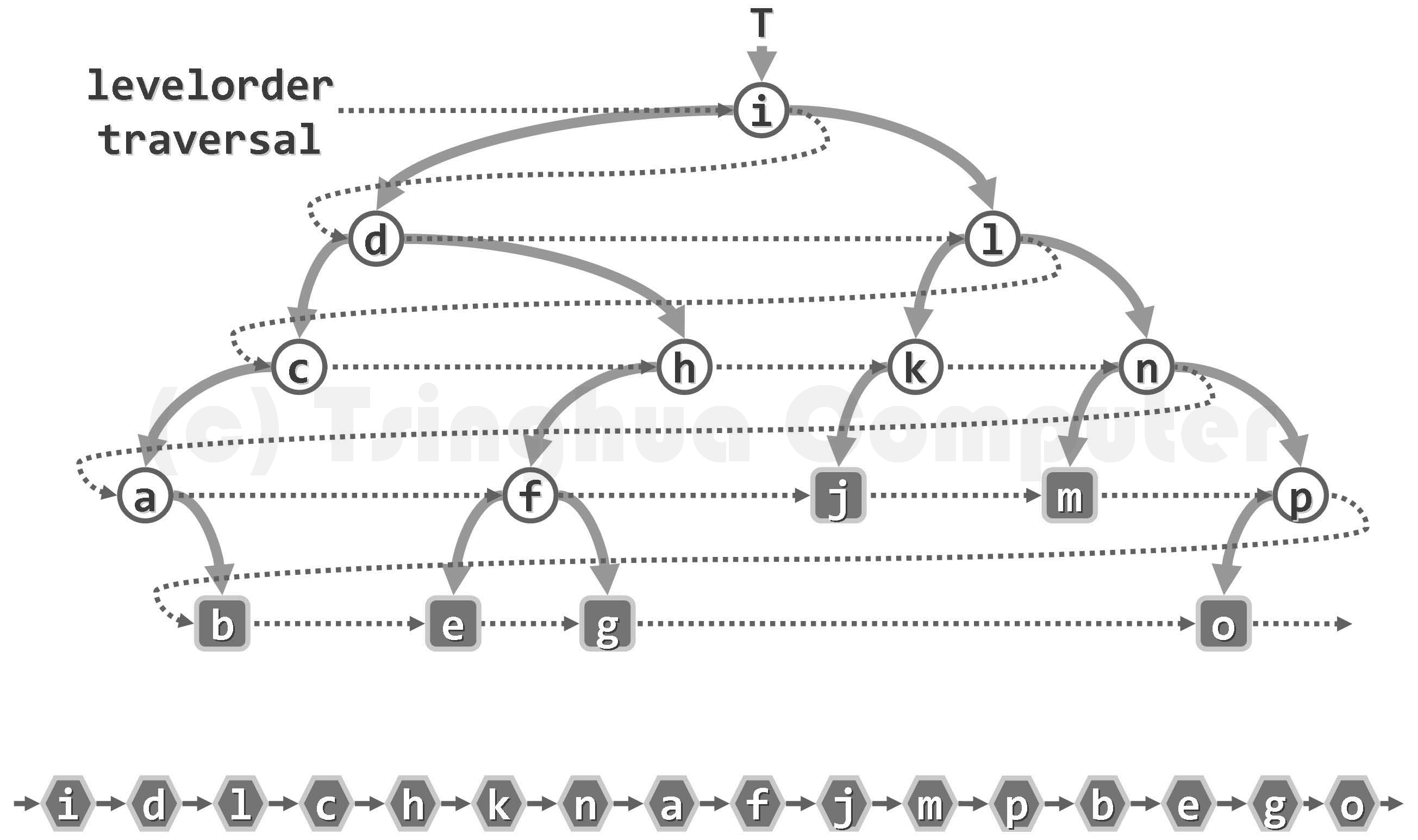
2.1 height of binary number of recursion

#include <iostream>
#include <queue>
#include <algorithm>
using namespace std;



struct Node {
	int data;
	Node * lchild, * rchild;
	Node(int x = 0) { data = x;lchild = rchild = NULL; }
	
	void setChildNode(Node *l,Node *r) {
		lchild = l;
		rchild = r;
	}		
};

void preorderTrav(Node * root){
	if (root == NULL)return;
	printf("%d", root->data);//Preorder traversal: access the root node first
	preorderTrav(root->lchild);
	preorderTrav(root->rchild);
 }

void inorderTrav(Node * root) {
	if (root == NULL)return;
	inorderTrav(root->lchild);
	printf("%d", root->data);//Middle order traversal: intermediate access root node
	inorderTrav(root->rchild);
}

void postoderTrav(Node* root) {
	if (root == NULL)return;
	postoderTrav(root->lchild);
	postoderTrav(root->rchild);
	printf("%d", root->data);//Post order traversal: the last access to the root node
}
//Explanation of level traversal: https://www.bilibili.com/video/BV1S54y1Y7Uq?from=search&seid=2361716283609621762&spm_id_from=333.337.0.0
//         A
//	  B            C
//D      E     F     G

//Hierarchical traversal (conditional pre order traversal, key: * t < = > node [n]; so as to better access the changing team top elements)
void levelTrav(Node* root) {
	if (root == NULL)return;
	
	//Establish queue Q
	queue <Node*> Q;
	
	//Root node enqueue ('A ')
	Q.push(root);
	//Loop out of the queue, queue in =================================================== > ⑤ return true when the queue is empty and exit the loop
	while (Q.empty() != true) {
		//Access the top element of the queue ① ('a ') = = = = = = > ② ('b') = = = = > ③ ('c ') = = = = > ④ ('DEFG')
		Node *t = Q.front();
		//Remove and print queue top element ① ('a ') = = = = = > ② ('b') = = = = > ③ ('c ') = = = = > ④ ('DEFG')
		Q.pop();
        printf("%d", t->data);
		
		//Left subtree queue ① ('b ') = = = = = = > ② ('d') = = = = > ③ ('f ') = = = = > ④ pass
		if (t->lchild != NULL)Q.push(t->lchild);
		//Right subtree queue ① ('c ') = = = = = = > ② ('e') = = = = > ③ ('g ') = = = = > ④ pass
		if (t->rchild != NULL)Q.push(t->rchild);
	}
	printf("\n");
}




int getTreeHigh(Node* root) {
	if (root == NULL)return 0;
	int LHigh = getTreeHigh(root->lchild);
	int RHigh = getTreeHigh(root->rchild);
	return max(LHigh, RHigh)+1;
}




int main() {
	Node *root = new Node(1);
	Node * Node2 = new Node(2);
	Node * Node3 = new Node(3);
	Node * Node4 = new Node(4);
	Node * Node5 = new Node(5);
	Node * Node6 = new Node(6);
	Node * Node7 = new Node(7);
	Node * Node8 = new Node(8);
	   //        1
    //      2              3
    //  4      5       null   7
  //null 8    6  null        
	root->setChildNode(Node2, Node3);
	Node2->setChildNode(Node4, Node5);
	Node3->setChildNode(NULL, Node7);
	Node4->setChildNode(NULL, Node8);
	Node5->setChildNode(Node6, NULL);


	preorderTrav(root);
	printf("\n");
	inorderTrav(root);
	printf("\n");
	postoderTrav(root);
	printf("\n");

	levelTrav(root);
	printf("\n");

	printf("Tree Height: %d\n", getTreeHigh(root));
}

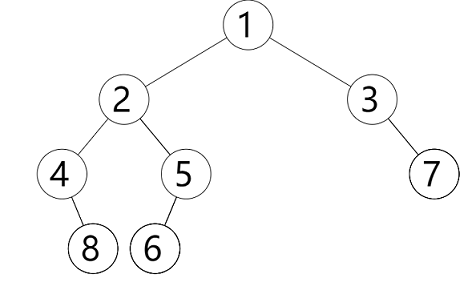
2.2 output and evaluation of recursive expression tree

Characteristics of expression tree: leaf nodes are operands, and non leaf nodes must be operators!

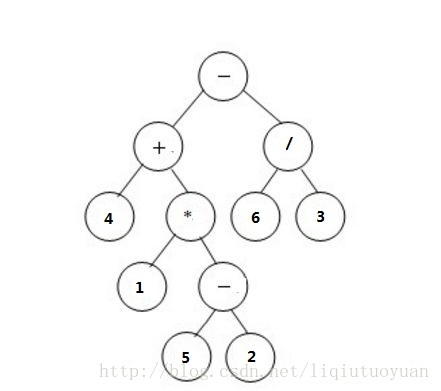
Input format:

The first line gives the number of nodes N, and the number of each node is 0 ~ N-1

Next N lines, each given separately:

Number of the node, operand / operator of the node, left child number and right child number of the node (- 1 means NULL)

Output format:

The first line outputs the infix expression of the expression tree, and the places in parentheses need to be enclosed in parentheses.

The second line outputs the prefix expression of the expression tree.

The second line outputs the suffix expression of the expression tree.

The fourth line outputs the calculation result of the expression tree, with two decimal places reserved.

Sample input:

11
0 - 1 2
1 + 3 4
2 / 5 6
3 4 -1 -1
4 * 7 8
5 6 -1 -1
6 3 -1 -1
7 1 -1 -1
8 - 9 10
9 5 -1 -1
10 2 -1 -1

Sample output:

(4+(1*(5-2)))-(6/3)
- + 4 * 1 - 5 2 / 6 3
4 1 5 2 - * + 6 3 / -
5.00

Full code:

#include <iostream>
using namespace std;
//Binary tree composition: operand (leaf node) + operator (others)
struct Node{
	char data;
	Node* lchild, * rchild;
};

//Prefix expression (preorder traversal)
void preOrder(Node* root) {	
	if (root == NULL) return;
	printf("%c ", root->data);
	preOrder(root->lchild);
	preOrder(root->rchild);
}
//Suffix expression (subsequent traversal)
void postOrder(Node *root) {
	if (root == NULL) return;
	postOrder(root->lchild);
	postOrder(root->rchild);
	printf("%c ", root->data);
}

//Infix expression (conditional middle order traversal)
void inOrder(Node *root,int layer){
	if (root == NULL)return;
    //Output target results: (4 + (1 * (5 - 2)) - (6 / 3)
    //Note: if there is no such conditional statement, the output result: (((4) + ((1) * (5) - (2)) - ((6) / (3));
	if (root->lchild == NULL && root->rchild == NULL) printf("%c", root->data);//Operands: leaf knot (clump) points
	else {
		if (layer > 0)printf("(");
	//Note: if this (int layer) parameter is not introduced, the output result: ((4 + (1 * (5-2)) - (6 / 3));
		inOrder(root->lchild,layer+1);
		printf("%c",root->data);
		inOrder(root->rchild,layer+1);
		if (layer > 0)printf(")");
	}
}




//Calculation function
double calc(double a, double b, char op) {
	switch (op){
	case '+':return a + b;
	case '-':return a - b;
	case '*':return a * b;
	case '/':return a / b;
	}
}
//Recursive algorithm: return calculation results
double calcExprTree(Node *root) {
	if (root == NULL)return 0;
	//When passing to the last layer (recursive boundary condition): that is, all leaf nodes, '5' - > 5, '2' - > 2;
	if (root->lchild == NULL && root->rchild == NULL)return root->data - '0';//Objects: leaf nodes
	double a = calcExprTree(root->lchild);
	double b = calcExprTree(root->rchild);
	//Calculate 5-2 and start to return to the first layer and return to the final result;
	return calc(a, b, root->data);
}




//User defined interactive interface: & Index 0-10& Corresponding index element value;
		//&The left index of the child node (- 1)& The index of the right child node of the corresponding index (- 1 represents NULL);
		//Sample input (in the user-defined interactive interface):
		//	    11
		//		0 (space) - (space) 1 (space) 2
		//		1 + 3 4
		//		2 / 5 6
		//		3 4 - 1 - 1
		//		4 * 7 8
		//		5 6 - 1 - 1
		//		6 3 - 1 - 1
		//		7 1 - 1 - 1
		//		8 - 9 10
		//		9 5 - 1 - 1
		//		10 2 - 1 - 1
		//      Sample output:
		//        (4 + (1 * (5 - 2)) - (6 / 3) (infix expression)
		//		-+ 4 * 1 - 5 2 / 6 3 (prefix expression)
		//		4 1 5 2 - * + 6 3 / - (suffix expression)
		//		5.00

int main() {
	//Define the total number of nodes N (including root nodes) through the user interaction interface;
	int N;
	scanf("%d/n", &N);
	
	//*Nodes [n] < = > tree structure Node [index and corresponding element value];
	Node* nodes = new Node[N];
	
	//Assignment * nodes[N]: through the loop structure and user interaction interface;
	for (int i = 0;i < N;i++) {
		int index;
		char data;
		int l, r;
		//User interaction interface;
		scanf("%d %c %d %d",&index, &data, &l, &r);
		
		//Assignment;
		nodes[index].data = data;
		nodes[index].lchild = (l != -1 ? &nodes[l] : NULL);
		nodes[index].rchild = (r != -1 ? &nodes[r] : NULL);
	}
	Node *root = &nodes[0];
	


	inOrder(root, 0);
	printf("\n");

	preOrder(root);
	printf("\n");

	postOrder(root);
	printf("\n");


	double ans = calcExprTree(root);
	printf("%.2f\n",ans);

	return 0;

}

2.3 recursively find the path from a node to the root node

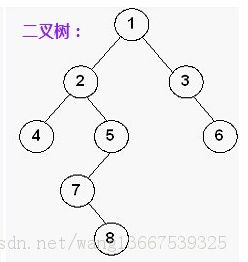
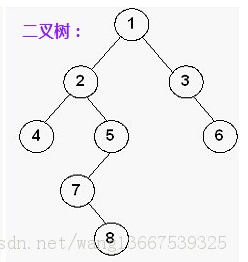
For the following binary tree, node 7 is located in layer 4, and its path to the following node is 1 2 5 7

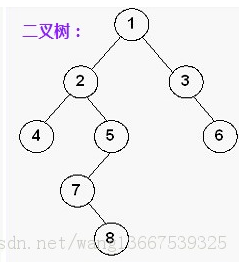
Find the number of layers of a node

First, simplify the problem and find the number of layers of the specified node in the binary tree (assuming that the number of layers of the root node is 1)

In order to record the layer number of the current access node, the following two methods can be adopted for the layer number:

Find node path

Complete code

For the following binary tree, node 7 is located in layer 4, and its path to the following node is 1 2 5 7

#include <iostream>
#include <vector>
using namespace std;

struct Node {
	int data;
	Node* lchild, * rchild;
	
	Node(int x = 0) { data = x;lchild = rchild = NULL; }

	void setChildNode(Node* l, Node* r) {
		lchild = l;
		rchild = r;
	}
};

/Find the number of layers of the node///
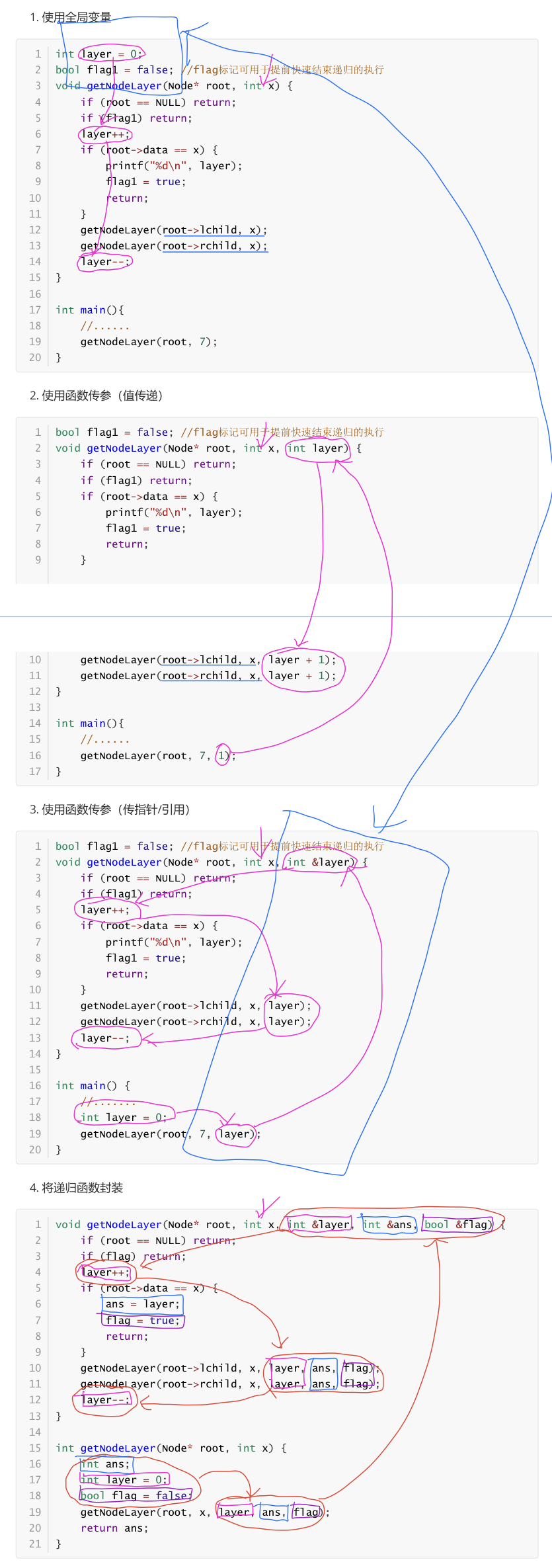
//Method 1: use global variables (int layer=0; heap space)

int layer = 0;//key1
bool flag1 = false;
//Preorder traversal architecture
void getNodeLayer(Node* root, int x) {
	if (root == NULL)return;
	
	//After finding x, flag1 is used to end recursive execution in advance;
	if (flag1)return;
	//The root node layer is 1;
	layer++;//key2
	if (root->data == x) {
		printf("%d\n", layer);
		flag1 = true;
		return;
	}
	getNodeLayer(root->lchild, x);
	getNodeLayer(root->rchild, x);

	//Every time you traverse to the end, the number of layers is reduced by one; Then go to the next traversal, and add one layer in turn
	layer--;//key3
}

//Method 2: use the function to transfer parameters (value transfer: getNodeLayer(root, x, layer + 1));
// getNodeLayer(root, 7, 1);//key1

//bool flag1 = false;
//void getNodeLayer(Node* root, int x, int layer) {//key2
//	if (root == NULL)return;
//
//	if (flag1 == true)return;
//	if (root->data == x) {
//		printf("%d", layer);
//		flag1 = true;
//		return;
//	}
//	getNodeLayer(root->lchild, x, layer + 1);//key3
//	getNodeLayer(root->rchild, x, layer + 1);//key4
//}





//Method 3: use function to pass parameters (pass pointer / reference: int & layer stack space) (understand)

//bool flag1 = false;
//void getNodeLayer(Node* root, int x, int & layer) {//key3
//	if (root == NULL)return;
//
//	layer++;//key4
//	if (root->data == x) {
//		printf("%d", layer);
//		flag1 = true;
//		return;
//	}
//	getNodeLayer(root->lchild, x, layer);
//	getNodeLayer(root->rchild, x, layer);
//
//	layer--;//key5
//}

//Method 4: encapsulate recursive functions (understand)
//void getNodeLayer(Node *root, int x, int &layer, int &ans, bool &flag1) {//key3
//	if (root == NULL)return;
//
//	layer++;//key4
//	if (flag1 == true)return;
//	if (root->data == x) {
//		ans = layer;
//		flag1 = true;
//		return;
//	}
//	getNodeLayer(root->lchild, x, layer, ans, flag1);
//	getNodeLayer(root->rchild, x, layer, ans, flag1);
//
//	layer--;//key5
//}
//int getNodeLayer(Node* root, int x) {
// //key1 (define reference variable)
//	int ans;
//	int layer = 0;
//	bool flag1= false;
key2
//	getNodeLayer(root, x,layer,ans, flag1);
// //key6 (output "interface")
//	return ans;
//}


/Find the node path (similar to finding the number of layers of the node)
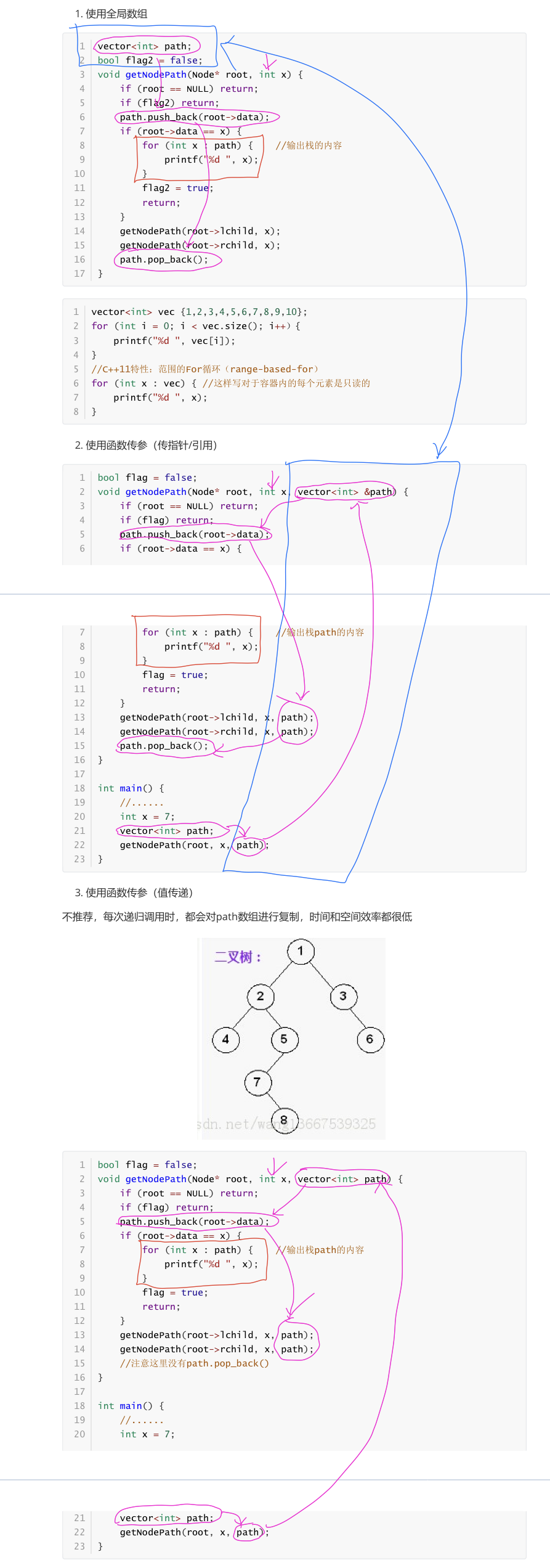
//Method 1: use global array

vector<int>path;//key1 global array

bool flag2 = false;
void getNodePath(Node* root, int x) {
	if (root == NULL)return;
	
	if (flag2)return;
	path.push_back(root->data);//key2 stack
	if (root->data == x) {
		for (int x : path) {C++11 Properties: of ranges For Circulation( range-based-for)
			printf("%d ", x);//key3 output stack
		}
		flag2 = true;
		return;
	}
	getNodePath(root->lchild, x);
	getNodePath(root->rchild, x);

	path.pop_back();//key4 out of stack
}

//Method 2: use function to pass parameters (pointer / reference)

//bool flag2 = false;
//Void getnodepath (node * root, int x, vector < int > & path) {/ / Key3 pointer array
//	if (root == NULL)return;
//
//	if (flag2)return;
//	path.push_back(root->data);//key4
//	if (root->data == x) {
//		for (int x : path) {
//			printf("%d ", x)；//key5
//		}
//      flag2 = true;
//		return;
//	}
//	getNodePath(root->lchild, x, path);
//	getNodePath(root->rchild, x, path);
//
//	path.pop_back();//key6
//}



//Method 3: it is not recommended to use function to pass parameters (value passing) (∵ each recursive call will copy the path array ∵ low time and space efficiency)

//bool flag2 = false;
//void getNodePath(Node* root, int x, vector<int>path) {//key3
//	if (root == NULL)return;
//
//	if (flag2)return;
//	path.push_back(root->data);
//	if (root->data == x) {
//		for (int x : path) {
//			printf("%d ", x);
//       }//key4
//		flag2 = true;
//		return;
//	}
//	getNodePath(root->lchild, x, path);
//	getNodePath(root->rchild, x, path);
//	//No path pop_ bach()
//}


int main() {
	Node* root = new Node(1);
	Node* node_2 = new Node(2);
	Node* node_3 = new Node(3);
	Node* node_4 = new Node(4);
	Node* node_5 = new Node(5);
	Node* node_6 = new Node(6);
	Node* node_7 = new Node(7);
	Node* node_8 = new Node(8);

	root->setChildNode(node_2, node_3);
	node_2->setChildNode(node_4, node_5);
	node_3->setChildNode(NULL, node_6);
	node_5->setChildNode(node_7, NULL);
	node_7->setChildNode(NULL, node_8);

/Find the number of layers of the node/
//Method 1
	int x = 7;
	getNodeLayer(root, x);
	
//Method 2
	//getNodeLayer(root, 7，1);
	
//Method 3
	//int layer=0;//key1
	// getNodeLayer(root, 7，layer);//key2
	
//Method 4
	//int getNodeLayer(Node * root, int x) {
	// //Key1 (define reference variable)
	//	int ans;
	//	int layer = 0;
	//	bool flag1 = false;
	// //key2
	//	getNodeLayer(root,x,layer,ans,flag1)
	//}
	// 
/Find the node path (similar to finding the number of layers of the node)
//Method 1
	getNodePath(root, x);
	printf("\n");
	
//Method 2
	//key1 defines reference variables
	//int x = 7;
	//vector<int>path;
	key2
	//getNodePath(root, x, path);
	
//Method 3
	//key1
	//int x = 7;
	//vector<int>path;
	//key2
	//getNodePath(root, x, path);

	return 0;
}

Writing method 1: vector<int> vec {1,2,3,4,5,6,7,8,9,10};
for (int i = 0; i < vec.size(); i++){
    printf("%d ", vec[i]);
}
//C++11 feature: range based For loop
 Method 2: for (int x : vec) {	//This is read-only for each element in the container
    printf("%d ", x);
}

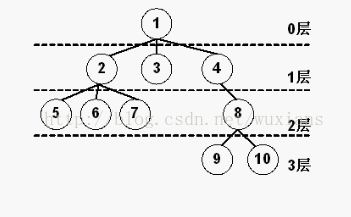
2.4 traversal of recursive ordinary tree

#include <iostream>
#include <vector>
#include <queue>
#include <initializer_list>
using namespace std;

struct Node {
	int data;
	//key1 uses pointer array to store multiple branches
	vector<Node*>child;

	Node(int x = 0) { data = x; }

	void setChildNode(initializer_list<Node*>list) {//C++11 features: initializer_ List (incoming list data, representing each branch node)
		//key2 uses loop and pointer array to establish multiple branches
		for (Node* x : list) {
			child.push_back(x);
		}
	}
};

//Preorder traversal 
void preOrder(Node* root) {
	if (root == NULL)return;

	printf("%d", root->data);
	//key3 uses loop and pointer array for recursion
	for (Node* x : root->child) {
		preOrder(x);
	}
}
//Postorder traversal
void postOrder(Node* root) {
	if (root == NULL)return;
	//key3
	for (Node* x : root->child) {
			preOrder(x);
		}
	printf("%d", root->data);
	
}





//level traversal 
void levelOrder(Node* root) {
	if (root == NULL)return;

	queue<Node*> Q;//Team building
	Q.push(root);//Join the team
	while(Q.empty() == false) {
		Node* t = Q.front();Q.pop();//Out of the team
		//key4: use * t < = > node * to transform the top elements of the team
		printf("%d", t->data);//Print top node elements
	    for (Node* x : t->child) {
		Q.push(x);//Join: the child node of the corresponding top node of the team
		}
	}
}


int main() {
	Node* root = new Node(1);
	Node* node_2 = new Node(2);
	Node* node_3 = new Node(3);
	Node* node_4 = new Node(4);
	Node* node_5 = new Node(5);
	Node* node_6 = new Node(6);
	Node* node_7 = new Node(7);
	Node* node_8 = new Node(8);
	Node* node_9 = new Node(9);
	Node* node_10 = new Node(10);

	root->setChildNode({ node_2,node_3,node_4 });
	node_2->setChildNode({ node_5,node_6,node_7 });
	node_4->setChildNode({ node_8 });
	node_8->setChildNode({ node_9,node_10 });

	preOrder(root);
	printf("\n");

	postOrder(root);
	printf("\n");

	levelOrder(root);
	printf("\n");

	return 0;
}

Recursive call principle

Function call stack instance: the main function main() calls funcA(), funcA() calls funcB(), and then funcB() calls itself (recursion)

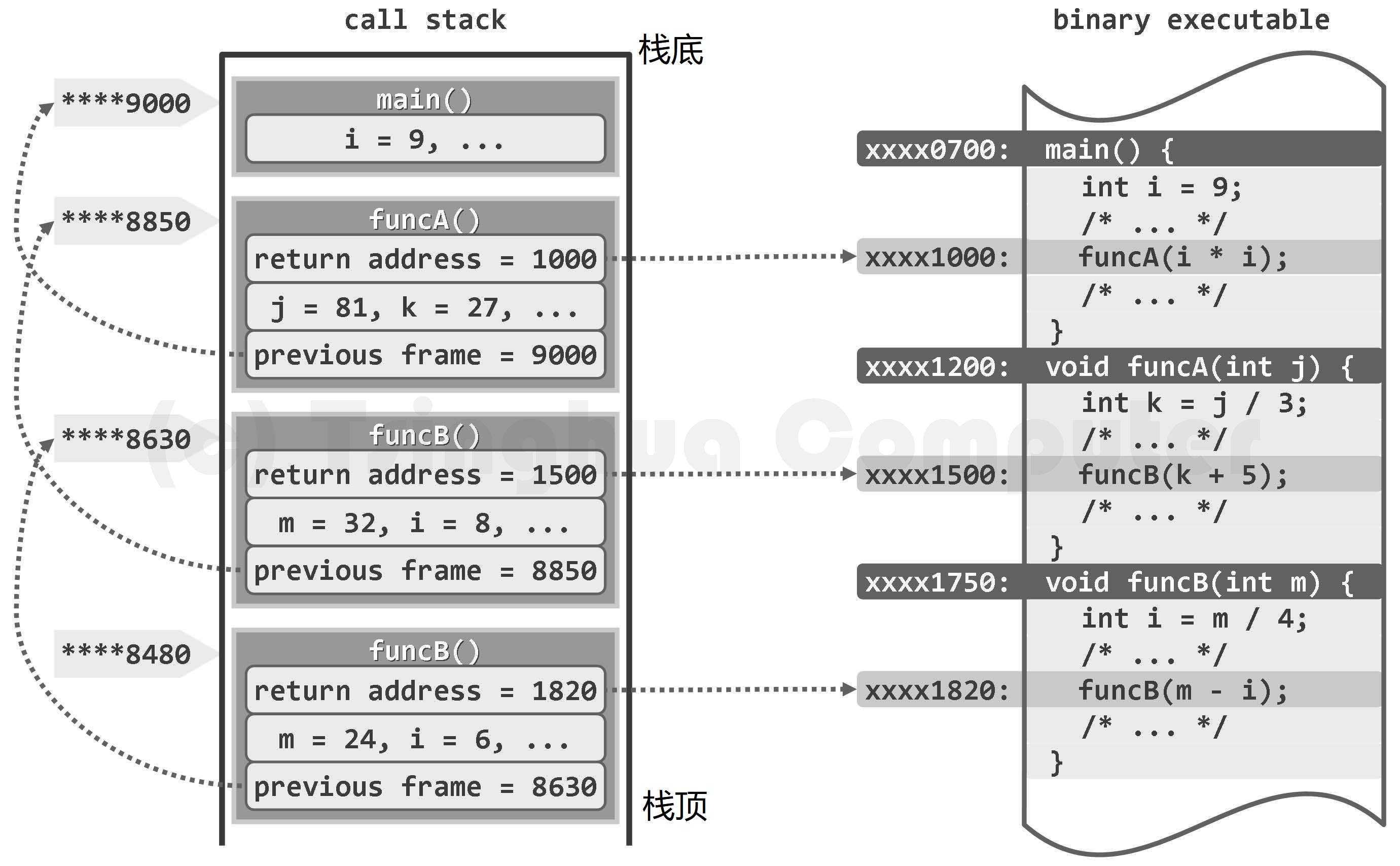
The basic unit of function call stack is frame. Each time a function is called, a frame will be created accordingly to record the return address, local variables, incoming parameters, etc. of the function instance in the binary program, and the frame will be pushed into the call stack. If a new call occurs before the function returns, similarly, press a frame corresponding to the new function into the stack to become the new top of the stack. Once the function runs, the corresponding frame pops up, and the operation control right will be handed back to the upper calling function of the function, and the position of continuing execution in the binary program will be determined according to the return address recorded in the frame.

At any time, each frame in the call stack corresponds to those call instances that have not been returned, that is, the active function instance at that time. In particular, the frame at the bottom of the stack must correspond to the entry main function (). If it pops up from the call stack, it means that the operation of the whole program is over, and then the control will be returned to the operating system.

In addition, each frame in the call stack needs to store other contents. For example, due to the different size of each frame, they also need to record the starting address of the previous frame to ensure that the previous frame can be restored correctly after it is out of the stack.

As a special form of function call, recursion can also be realized with the help of the above call stack. For example, in the above figure, the self call corresponding to funcB() will also be pressed into a new frame. It can be seen that the same function may have multiple instances at the same time and occupy a frame in the call stack. The structures of these frames are identical, but the parameters or variables with the same name are independent copies. For example, in the two instances of funcB(), the entry parameter m and the internal variable i each have a copy.

(III) DFS / backtracking algorithm

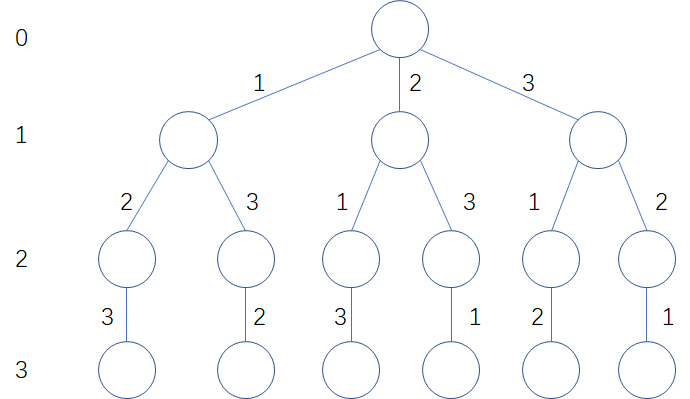
If the solution of a problem can be obtained by multiple steps, and each step has several choices (these candidate scheme sets may depend on the previous choices), and can be implemented by recursive enumeration method, its working mode can be described by solution tree.

3.1 Full Permutation Problem of backtracking algorithm (depth first search)

All full permutations that can be composed of output numbers 1~N

#include <iostream>
#include <vector>
using namespace std;
const int MAXn = 10;

bool isused[MAXn];//Use inspection
vector<int>num;//Set num array
int N;//Data range (1-3)

void DFS(int index){
	//Boundary conditions for each recursion
	if (index >= N) {
		for (int x : num) {
			printf("%d", x);
		}
		printf("\n");
		return;
    }


    //Explanation of core ideas: https://www.bilibili.com/video/BV1ct411u7Qi?from=search&seid=11426884062134919798&spm_id_from=333.337.0.0
	for (int i = 1;i <= N;i++) {
	if (isused[i])continue;
	//① 1 join the team (index=0)
	num.push_back(i);
	//② Setting 1 has been used
	isused[i] = true;
	//③ Index = 1 - > n-2 make full arrangement
	DFS(index + 1);
	
	//④ 1 out of the team
	num.pop_back();
	//⑤ Setting 1 is not used
	isused[i] = false;
	}
}

int main() {
	N = 3;
	DFS(0);//Enter 0 layer
	return 0;
}

Prime ring problem

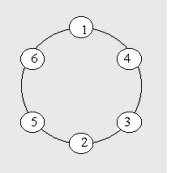
Enclose n integers from 1 to n into a ring. If any two adjacent numbers are added and the result is prime, then the ring becomes prime.

For example, a prime ring composed of numbers 1-6 is represented by an array as [1, 4, 3, 2, 5, 6] (the first bit is fixed as 1)

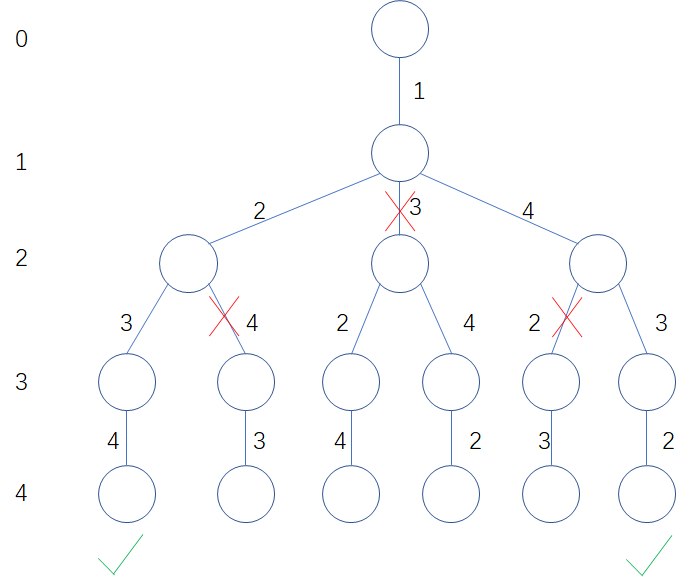
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int MAXN = 100;

bool isPrimeNum[MAXN];/key1 Prime number test 

bool isUsed[MAXN];//Use inspection
vector<int> num;//ans array
int N;//Data range (1-4)
	  
	  
///Finding prime number by key2 screening method
void getPrimeTable() {
	//Let's assume that they are prime numbers
	fill(isPrimeNum, isPrimeNum + MAXN, true);//Set the splicing array to true
	isPrimeNum[0] = isPrimeNum[1] = false;//And define 0 and 1 as non prime numbers

	for (int i = 2;i < MAXN;i++) {
		if (isPrimeNum[i]) {
			/key3 if i Is a prime number: a i All multiples of are set to non prime numbers(An integer multiple of a prime number is not a prime number)；
			for (int j = i+i; j < MAXN;j += i) {//key2 j+=i;
				isPrimeNum[j] = false;
			}
		}
	}
}


void DFS(int index) {
	//Recursive boundary condition
	if (index >= N) {
        key4 Judge whether the first number and the last number are prime after being added;
		int temp = num[0] + num[index - 1];key4-1 there index-1 Index the tail element;
		if (isPrimeNum[temp] == false)return;
		//If yes: print array
		for (int x : num) {
			printf("%d", x);
		}
		printf("\n");
		return;
	}
	
	for (int i = 2;i <= N;i++) {
		if (isUsed[i])continue;
		
		//Pruning: if the sum of adjacent elements is not prime, directly jump out of the loop;
		int temp = i+ num[index - 1]; //key4-2 index-1 here is the index of adjacent elements;
		if (isPrimeNum[temp] == false) {
			continue;
		}
		num.push_back(i);
		isUsed[i] = true;
		DFS(index + 1);

		num.pop_back();
		isUsed[i] = false;
	}
}


int main() {
	getPrimeTable();

	N = 4;
	num.push_back(1);

	DFS(1);


	return 0;
}

3.3 eight queens problem of backtracking algorithm (depth first search)

The eight queens problem is a problem with the background of chess: how can it be in 8 × Eight queens are placed on the chess board of 8, so that no queen can directly eat the other queens? In order to achieve this goal, no two Queens can be in the same horizontal, vertical or diagonal line. The eight queens problem can be extended to a more general N Queens placement problem: at this time, the size of the chessboard becomes n × n. And N queens. If and only if n = 1 or n ≥ 4, the problem has a solution.

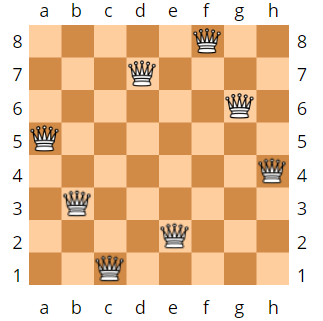
#include <cstdio>
#include <algorithm>
using namespace std;

const int MAXN = 100;
int solution[MAXN];//Record position j in line i
int cnt;//Total number of methods
int N;//Queen N


//key1 defines a chessboard for visual display of various methods
char chessboard[MAXN][MAXN];
void printSolution() {
	fill(chessboard[0], chessboard[0] + MAXN * MAXN,'*');//Initialize chessboard as*
	
	//Through the for loop: find all queen positions on the chessboard J - > define all queen positions as#
	for (int i = 0;i < N;i++) {
		int j = solution[i];//Find: find the Queen's position j in line I through solution[i]
		chessboard[i][j] = '#';//Definition: after searching, define the queen position as#
		chessboard[i][N] = '\0';
	}
	printf("solution #%d\n", cnt);
	//Through the for loop: print * chessboard and all # queens
	for (int i = 0;i < N;i++) {
		printf("%s\n", chessboard[i]);//Print: * chessboard and # queen
	}
	printf("\n");
}


//key2 determines whether the (row, col) position is within the attack range of all former queens. If it is, false will be returned;
bool judge(int row, int col) {
	//Through the for loop: find all queen positions j in the first row and judge whether the (row, col) position is in the attack position
	for (int i = 0;i < row;i++) {
		//Find: find the Queen's position j in line I through solution[i]
		int j = solution[i];
		//Judgment: same column, slash (sub diagonal, main diagonal)
		//Note: peer checking is not required - in the process of single-layer search, each layer recursion will only select one element in the for loop (that is, the same line), so there is no need to duplicate.)
		if (j == col || row + col == i + j || row - col == i - j)
			return false;
	}
	return true;
}


void DFS(int row) {
	//Boundary conditions for each recursion
	if (row >= N) {
		cnt++;//One successful recursion means one more solution;
		printSolution();//Visualize the solution
		return;
	}
	//core
	for (int col = 0;col < N;col++) {
		//Conflict: down loop
		if (judge(row, col) == false)continue;
		
		//No conflict: solution[row]=col, that is, define the queen position of row as col;
		solution[row] = col;
		DFS(row + 1);//For each layer of recursion, only one element in the for loop (that is, the same line) will be selected
	}
}

int main() {
	N = 8;
	DFS(0);
	printf("N=%d,total solutions:%d\n", N, cnt);
	return 0;
}