Precise coverage problem:
Given a matrix composed of 0 and 1, can we find a set of rows so that each column in the set contains exactly one 1.

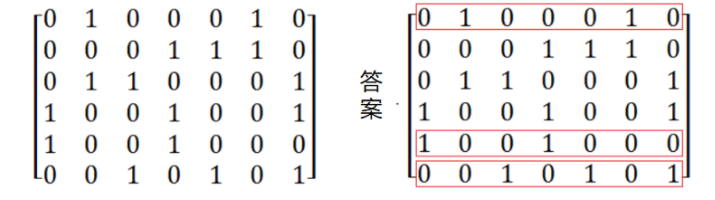
This kind of problem is a classical exact covering problem, which belongs to NP complete problem without polynomial algorithm.

Backtracking exhaustive:

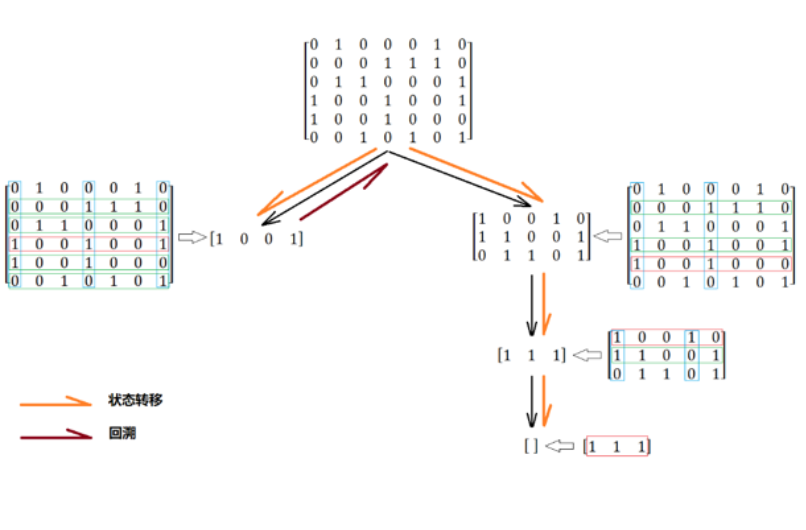
1. Select the first row (red), and the elements that will conflict with 1 in the same column are marked in blue.
   

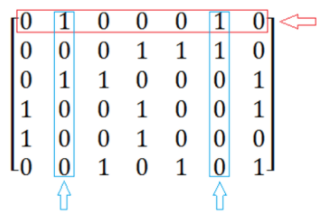
2. From the column view, there are also 1 rows marked in blue. These rows cannot be selected and are marked in green.
   

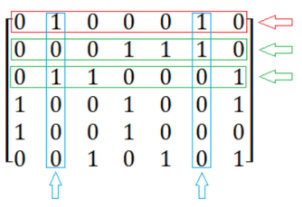
3. After selecting the first line of red, blue and green will not be considered, so the red record will be deleted, and the problem will be simplified.
   

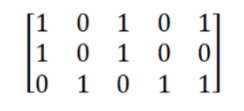
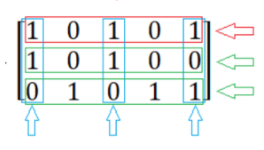
4. Continue to solve this small-scale matrix in the same way.
   Reduce the scale of the problem again. After deletion, the remaining matrix becomes an empty matrix.
   Two rows are selected in this search. The number of columns with '1' in the selected row is 5, and the total number of columns is 7. Therefore, this scheme fails.
   

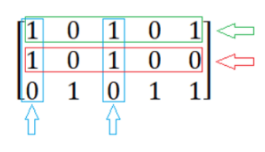
5. Go back and select the second line.
   Reduce the scale of the problem, and the rest is a 1 * 3 matrix, and the three numbers are '1'.
   Obviously, this line is a must.
   So far, a feasible solution with accurate coverage is found.
   

The traditional two-dimensional array is used to store the matrix, but the time complexity of searching and deleting backtracking is very high, the understanding is cumbersome, and the implementation is easy to make mistakes.

Dancing Links

A chained data structure, which uses the nature of linked list and is properly used in cache and backtracking matrix without additional space.
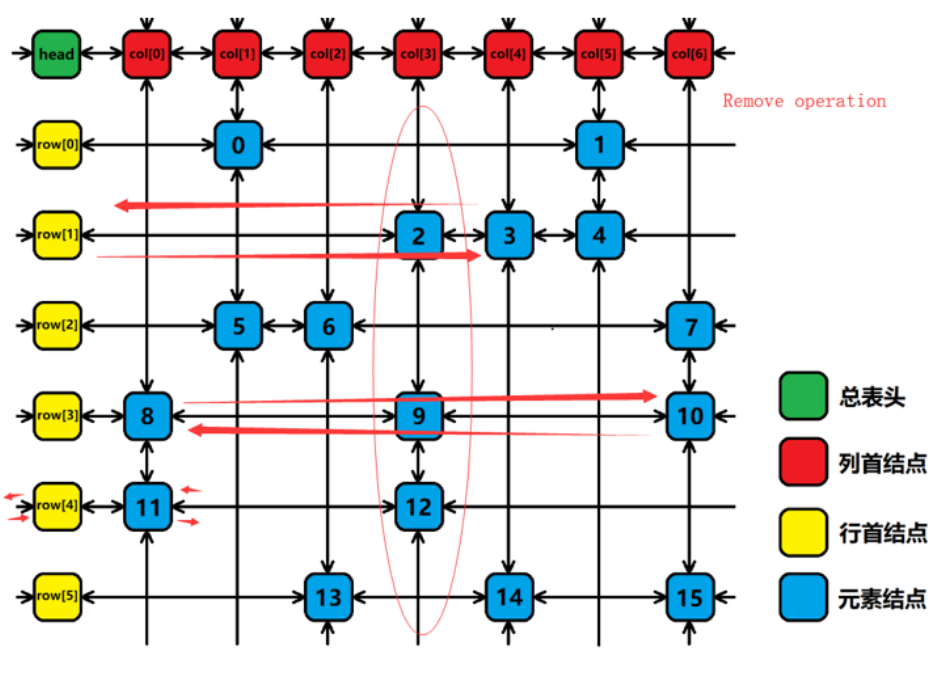
In the matrix stored in this structure, column deletion is O(1) and row deletion is o ©.
It is named because the operation of deleting and restoring is a jump between pointers, like a delicate dance.

Delete algorithm:
The right direction of the left node of x points to the right node of x
The left direction of the right node of x points to the left node of x

Recovery algorithm:
The right direction of the left node of x points to x
The left direction of the right node of x points to x

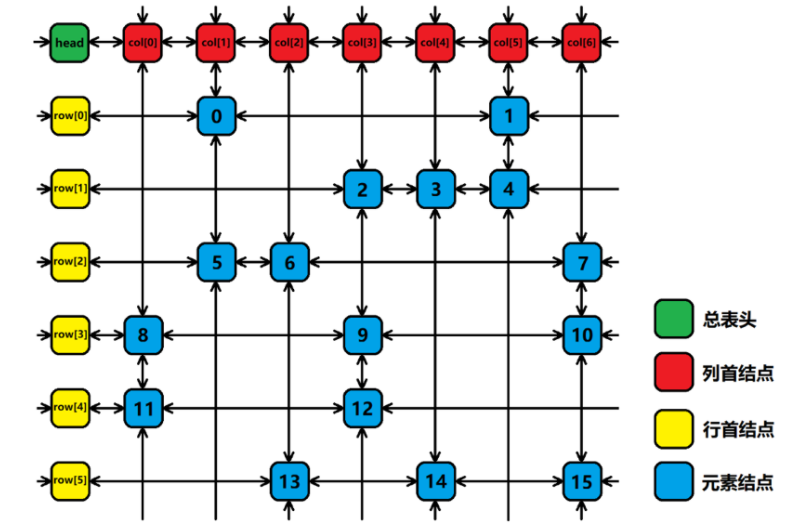
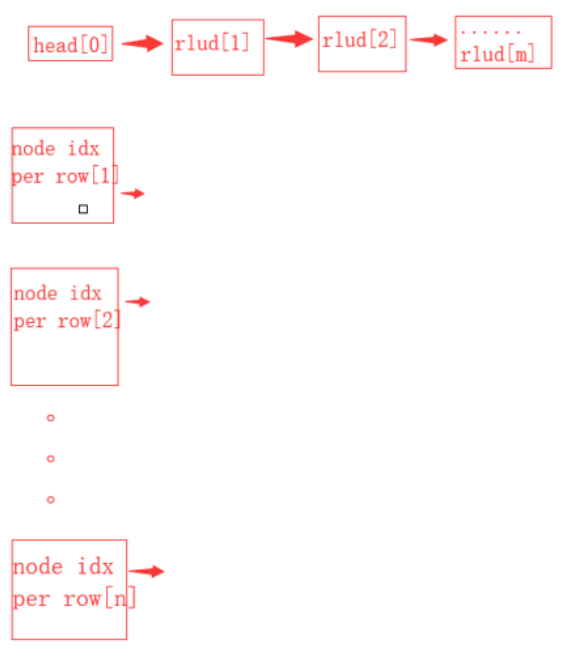
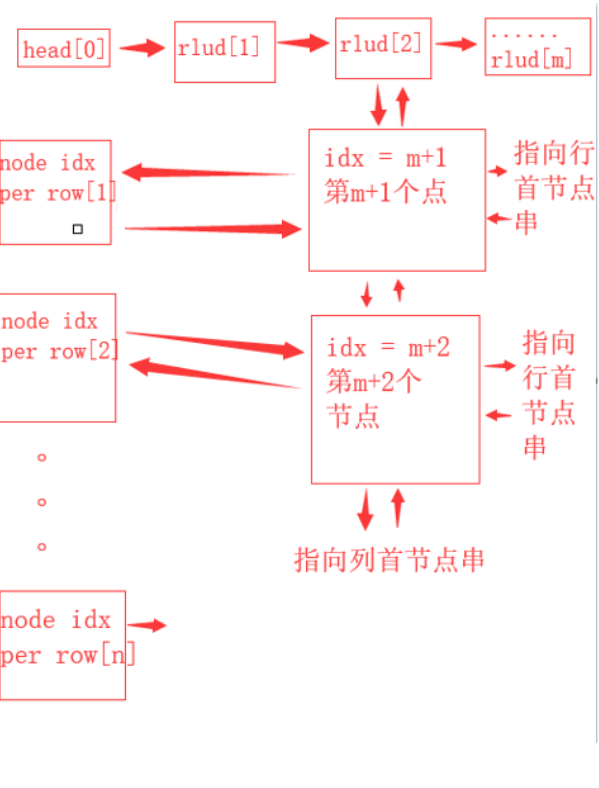
The data structure representation of the cross two-way circular linked list of the matrix:
The left and right boundaries of all arrows are connected circularly (the upper and lower boundaries are also connected circularly).
Each element node represents the '1' in the original matrix, that is, the blue square in the figure, in which the number represents the number in the corresponding memory pool.
During initialization, the left and right pointers of all row head nodes and the up and down pointers of column head nodes point to themselves.
Then read the matrix in the order of increasing rows and columns respectively, and execute the row node insertion operation when reading '1', which corresponds to the increasing order of the blue node in the figure.

initialization

Insert Knot

Delete, restore

Selecting (dancing)

Code template

struct DLX
{
	int n, m, idx;	//Number of rows, columns, element index
	int l[MAX_NUM], r[MAX_NUM], u[MAX_NUM], d[MAX_NUM];	//Record the indexes up, down, left and right of an idx index point
	int col[MAX_NUM], row[MAX_NUM];	//Record the row and column number of an index point
	int nodeIdxPerRow[MAX_NUM];	//Record the index of the node at the beginning of each line
	int nodeNumPerCol[MAX_NUM];	//Record the number of nodes in each column
	int ansd, ans[MN];
	
	void init(int n, int m)	//Initialize the header node and column node header string of the cross linked list
	{
		for (int i = 0; i <= m; ++i)	//Header node number group index = 0, column node header has m indexes in total, 1~m
		{
			r[i] = i + 1;
			l[i] = i - 1;
			u[i] = d[i] = i;	//The knot nodding strings are only horizontally connected with each other, and the upper and lower connections point to themselves
		}
		r[m] = 0;	//Loop connection, the right end of col[m] points to the head node
		l[0] = m;	//The left end of the head node points to col[m]
		
		memset(nodeIdxPerRow, 0, sizeof(nodeIdxPerRow));
		memset(nodeNumPerCol, 0, sizeof(nodeNumPerCol));
		
		idx = m + 1;	//At present, 0 header node and m column node header strings are used. There are m+1 nodes in total from 0 to M
	}
	
	void link(int insertRow, int insertCol)	//Insert some data records made by the node
	{
		//Update column
		nodeNumPerCol[insertCol]++;	//Insert a node, then the number of nodes in this column + 1
		row[idx] = insertRow;
		col[idx] = insertCol;	//Record the row and column of the idx node
		u[idx] = insertCol;	//Point up to the insertCol of the string
		d[idx] = d[insertCol];	//Downward pointing to the downward pointing point of the original nodal string
		u[d[insertCol]] = idx;	//The node pointed to by the original column node string is upward, and the node pointed to by the column node node string is pointed to the inserted node (using index)
		d[insertCol] = idx;	//The column node string points down to the newly inserted node (using index)
		
		//Update row
		if (!nodeIdxPerRow[insertRow])	//If the node is the first inserted node
			nodeIdxPerRow[insertRow] = r[idx] = l[idx] = idx;	//There is no point in this line. Join directly
		else
		{
			r[idx] = nodeIdxPerRow[insertRow];	//The right end of the new node points to the first node in the original row record
			l[idx] = l[nodeIdxPerRow[insertRow]];	//The left end of the new node points to the left end of the first node of the original row record
			r[l[nodeIdxPerRow[insertRow]]] = idx;	//The left end and the right end of the first node of the original row record point to the newly inserted point (using index)
			l[nodeIdxPerRow[insertRow]] = idx;	//The left end of the first node of the original row record points to the newly inserted node (using index)
		}
		idx++;
		return ;
	}
	
	void remove(int deleteCol)	//Deleting a set involving column c connects the left and right ends of the column to be deleted, which is also equivalent to removing itself
	{
		r[l[deleteCol]] = r[deleteCol], l[r[deleteCol]] = l[deleteCol];
		for (int i = d[deleteCol]; i != deleteCol; i = d[i])
			for (int j = r[i]; j != i; j = r[j])
			{
				u[d[j]] = u[j];
				d[u[j]] = d[j];
				nodeNumPerCol[col[j]]--;
			}
	}
	
	void resume(int resCol)	//Restore the set involving column c
	{
		for (int i = u[resCol]; i != resCol; i = u[i])
			for (int j = l[i]; j != i; j = l[j])
			{
				u[d[j]] = j;
				d[u[j]] = j;
				nodeNumPerCol[col[j]]++;
			}
		r[l[resCol]] = resCol;
		l[r[resCol]] = resCol;
	}
	
	bool dance(int deep)	//Row d selected
	{
		if (!r[0])	//All covered
		{
			ansd = deep;
			return 1;
		}
		int c = r[0];	//The first column to which the header node points
		for (int i = r[0]; i != 0; i = r[i])	//Enumeration column header pointer
			if (nodeNumPerCol[i] < nodeNumPerCol[c])
				c = i;
		remove(c);	//Delete the column
		for (int i = d[c]; i != c; i = d[i])	//Enumerate the elements of the column
		{
			ans[deep] = row[i];	//Record the row of this column element
			for (int j = r[i]; j != i; j = r[j])
				remove(col[j]);	//Delete the column of the element on the row of an element in the column
			if (dance(deep + 1))
				return 1;
			for (int j = l[i]; j != i; j = l[j])
				resume(col[j]);
		}
		resume(c);
		return 0;
	}
}

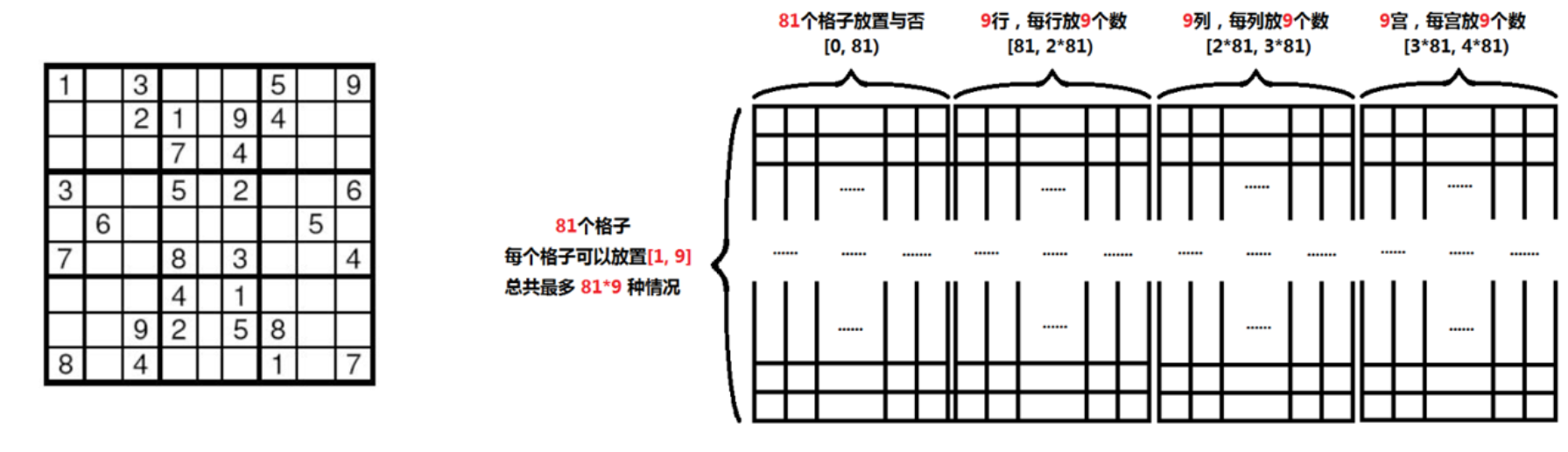
Sudoku problem is transformed into exact coverage matrix:

The row represents all cases of the problem, and the column represents the constraints of the problem.

The number that can be filled in each grid is 1 ~ 9. There are 9 * 9 (3 ^ 2 * 3 ^ 2) grids in total, and the total number of cases is 729.

That is, the number of lines of Dancing Links is 729.

There are four types of columns:

1. [0, 81) columns, respectively corresponding to whether 81 cells are placed with numbers
2. [82, 2 * 81) columns correspond to 9 rows respectively, and the placement of [1, 9] numbers in each row
3. [2 * 81, 3 * 81) columns correspond to 9 columns respectively, and the placement of [1, 9] numbers in each column
4. [3 * 81, 4 * 81) columns correspond to 9 "palaces" respectively, and the placement of [1, 9] numbers in each "Palace"

So the total number of columns is 4 * 81 = 324 columns