Topic link: https://cn.vjudge.net/problem/CodeForces-877E

The main idea of the topic

There is a tree with 1-bit root node, each node has a lamp, or on or off, m operations, get x, which means to find X and its subtree, the number of lights on, pow x, which means to change the state of X and its subtree lamp, that is, 1 to 0, 0 to 1.

Analysis

We learned the dfs order through this question. The idea of dfs ordering is to start with the root node and record the serial number of the first and last encounters of each node. The array in [] represents the first encounter and the array out [] represents the last encounter. So in the process of traversing, when you come to a node, you must first traverse its subtree, then return to the previous level. Suppose that when you encounter an X node, the serial number is 2 and the X subtree has four nodes. When you traverse all the subtree nodes, the serial number becomes 6. Then the interval of 2-6 can represent x and its subtree, so you can put it in the line segment tree to solve it. It's settled.

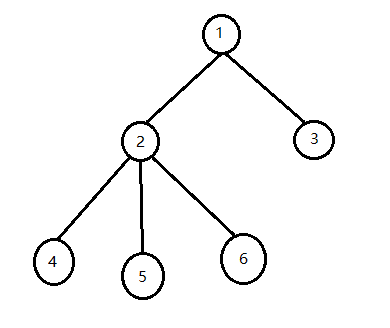
As shown in the figure, suppose we start from 1 and walk 2 first, then when we first meet 2 nodes, the serial number is 2, followed by subtree, 4 nodes correspond to 3, 5 correspond to 4, 6 correspond to 5, then 2-5 is the interval between 2 nodes and their subtrees so that we can put it into the online segment tree.

Code

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 200010;
int n, m, cnt, tot;
int in[N], out[N], head[N], t[N], num[N];
struct node{
	int l, r, sum, lazy;
}tr[N<<2];
struct Edge{
	int to, nxt;
}edge[N];
void add(int a, int b)
{
	edge[cnt].to = b;
	edge[cnt].nxt = head[a];
	head[a] = cnt++;
}
void pushup(int m)
{
	tr[m].sum = tr[m<<1].sum + tr[m<<1|1].sum;
}
void pushdown(int m)
{
	if(tr[m].lazy)
	{
		tr[m<<1].lazy ^= 1;
		tr[m<<1|1].lazy ^= 1;
		tr[m<<1].sum = tr[m<<1].r - tr[m<<1].l + 1 - tr[m<<1].sum;
		tr[m<<1|1].sum = tr[m<<1|1].r - tr[m<<1|1].l + 1 - tr[m<<1|1].sum;
		tr[m].lazy = 0;
	}
}
void build(int m, int l, int r)
{
	tr[m].l = l;
	tr[m].r = r;
	tr[m].lazy = 0;
	if(l == r)
	{
		tr[m].sum = t[num[l]];
		return ;
	}
	int mid = (l + r) >> 1;
	build(m<<1, l, mid);
	build(m<<1|1, mid + 1, r);
	pushup(m);
}
void updata(int m, int l, int r)
{
	if(tr[m].l == l && tr[m].r == r)
	{
		tr[m].sum = r - l + 1 - tr[m].sum;
		tr[m].lazy ^= 1;
		return ;
	}
	pushdown(m);
	int mid = (tr[m].l + tr[m].r) >> 1;
	if(r <= mid) updata(m<<1, l, r);
	else if(l > mid) updata(m<<1|1, l, r);
	else
	{
		updata(m<<1, l, mid);
		updata(m<<1|1, mid + 1, r);
	}
	pushup(m);
}
int query(int m, int l, int r)
{
	if(tr[m].l == l && tr[m].r == r) return tr[m].sum;
	pushdown(m);
	int mid = (tr[m].l + tr[m].r) >> 1;
	if(r <= mid) return query(m<<1, l, r);
	else if(l > mid) return query(m<<1|1, l, r);
	else return query(m<<1, l, mid) + query(m<<1|1, mid + 1, r);
}
void dfs(int x)
{
	in[x] = ++tot;//First encounter 
	num[tot] = x;//num[tot]=x denotes that in the new sequence, tot is the original x point. 
	for(int i = head[x]; i != -1; i = edge[i].nxt)
		dfs(edge[i].to);
	out[x] = tot;//Last encounter 
}
int main()
{
	scanf("%d", &n);
	cnt = tot = 0;
	memset(head, -1, sizeof head);
	for(int i = 2; i <= n; i++)
	{
		int p;
		scanf("%d", &p);
		add(p, i);
	}
	for(int i = 1; i <= n; i++) scanf("%d", &t[i]);
	dfs(1);
	build(1, 1, tot);
	scanf("%d", &m);
	char s[2];
	int x;
	while(m--)
	{
		scanf("%s %d", &s, &x);
		if(s[0] == 'g') printf("%d\n", query(1, in[x], out[x]));
		else updata(1, in[x], out[x]);
	}
	return 0;
}