1. Content
The operation has been completed. Here are some codes to share.
2. T2
1. ORB extraction
void computeAngle(const cv::Mat &image, vector<cv::KeyPoint> &keypoints) {
int half_patch_size = 8;
// int half_boundry = 16;
int bad_points =0; //A point in a corner where an angle cannot be calculated
for (auto &kp : keypoints) {
// START YOUR CODE HERE (~7 lines)
int u=kp.pt.x, v = kp.pt.y;
if(u>=half_patch_size && v>=half_patch_size && u+half_patch_size<=image.cols && v+half_patch_size<=image.rows)
{
float m01=0, m10=0;
for(int i=u-half_patch_size; i < u + half_patch_size; ++i) //Traverse 16 points in x direction (right)
for(int j=v-half_patch_size; j < v + half_patch_size; ++j) //Traverse 16 points in y direction (bottom)
{
m10 +=i * image.at<uchar>(j, i);
m01 +=j * image.at<uchar>(j, i);
}
//Calculate the angle (in radians) and convert it to an angle
kp.angle = (float)std::atan(m01/m10) * 180/pi ; //Or std::atan2(m01, m10)*180/pi;
}
// END YOUR CODE HERE
}
return;
}
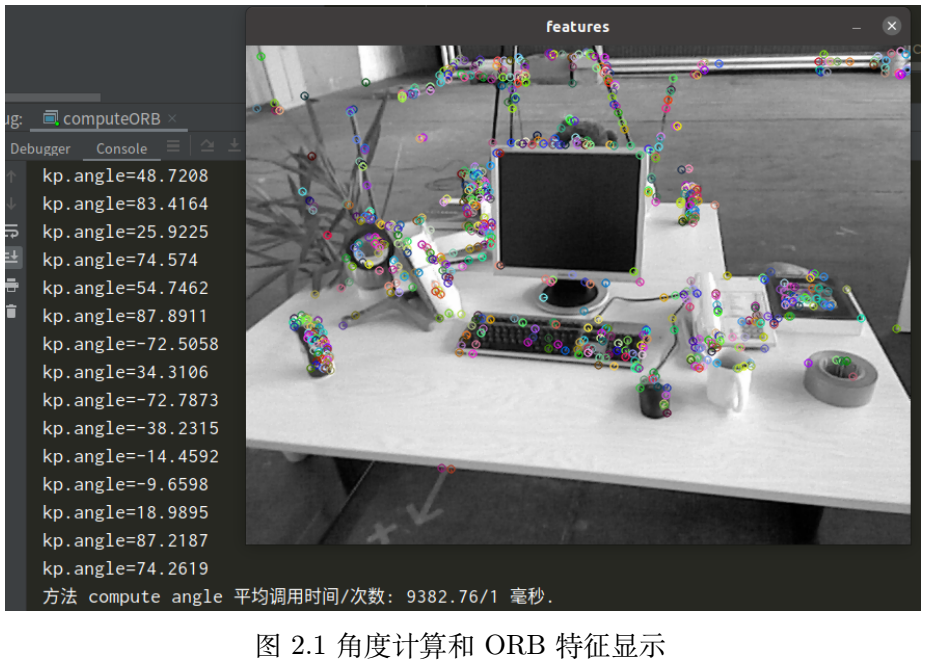
2. ORB description
void computeORBDesc(const cv::Mat &image, vector<cv::KeyPoint> &keypoints, vector<DescType> &desc)
{
int half_patch_size = 8, bad_points = 0;
for (auto &kp : keypoints)
{
int u = kp.pt.x, v = kp.pt.y;
DescType d(256, false); //256 bit descriptor
//STEP1: check whether the boundary is exceeded
if(u>=half_patch_size && v>=half_patch_size && u+half_patch_size<=image.cols && v+half_patch_size<=image.rows)
{
//STEP2: if it does not cross the boundary, collect the points according to the pattern, rotate the points P, q - > p',q', in combination with the directional angle theta of the feature points, calculate the coordinates of p',q', and compare the size. The result is the result of the bit descriptor (0 or 1)
for (int i = 0; i < 256; i++)
{
// START YOUR CODE HERE (~7 lines)
//Find the subscript of point pattern
cv::Point2f p(ORB_pattern[i * 4], ORB_pattern[i * 4 + 1]);
cv::Point2f q(ORB_pattern[i * 4 + 2], ORB_pattern[i * 4 + 3]);
//Using sin,cos, the angle is converted to radians * pi/180
double theta = kp.angle * pi / 180;
double cos_theta = cos(theta) , sin_theta = sin(theta);
int u_p_ = (int)(cos_theta * p.x - sin_theta * p.y) + u;
int v_p_ = (int)(sin_theta * p.x + cos_theta * p.y) + v;
int u_q_ = (int)(cos_theta * q.x - sin_theta * q.y) + u;
int v_q_ = (int)(sin_theta * q.x + cos_theta * q.y) + v;
//Judge whether the rotated p and q obtained according to the key point are out of bounds. If they are out of bounds, the descriptor is cleared and invalid
if(u_p_<0 || v_p_<0 || u_p_ >image.cols || v_p_ > image.rows || u_q_<0 || v_q_<0 || u_q_ >image.cols || v_q_ > image.rows)
{
d = {};
break; //Jump out of descriptor loop
}
d[i] = image.at<uchar>(v_p_, u_p_) > image.at<uchar>(v_q_, u_q_) ? false : true; //The former takes false and the latter takes true. The vector random accessor is not fast enough, but mastering the algorithm is the key
}
}
//Do not use when crossing the boundary
else
{
++bad_points;
d.clear();
};
desc.push_back(d);
// END YOUR CODE HERE
}
cout << "bad/total: " << bad_points << "/" << desc.size() << endl;
return;
}
3. Violence matching
// brute-force matching
void bfMatch(const vector<DescType> &desc1, const vector<DescType> &desc2,
vector<cv::DMatch> &matches) {
int d_max = 50;
// START YOUR CODE HERE (~12 lines)
// find matches between desc1 and desc2. The core method is bitwise XOR ^, but here it is judged according to each bit of vector < bool >
for(size_t i1=0; i1<desc1.size(); ++i1)
{
if(desc1[i1].empty()) continue;
cv::DMatch m{i1, 0, 256}; //DMatch(int _queryIdx, int _trainIdx, float _distance): _ Queryidx: match the i1 point_ Trainidx: the matching point of the target point is the 0_ Distance: the minimum distance is initialized to 256
for(size_t i2=0;i2<desc2.size();++i2)
{
if(desc2[i2].empty()) continue;
int hanming_distance = 0;
for(unsigned int j=0; j!=256; ++j) //Violence matches all key points in desc1 and desc2
{
hanming_distance += desc1[i1][j] ^ desc2[i2][j]; //Distance increases when unequal
}
if(hanming_distance<d_max && hanming_distance<m.distance) //If the distance meets the threshold and is less than the current distance, update the minimum distance and the best matching point
{
m.queryIdx = i1; //Matched point
m.trainIdx = i2; //Update best match points
m.distance = hanming_distance; //Update minimum distance
}
}
//Match successful
if(m.distance<d_max)
matches.push_back(m);
}
// END YOUR CODE HERE
// for (auto &m : matches) {
// cout << m.queryIdx << ", " << m.trainIdx << ", " << m.distance << endl;
// }
return;
}
4. Multithreaded ORB
The results are shown in the figure

This part mainly installs gcc, g + + and tbb libraries according to the documents given by the teaching assistant in the group (if necessary, you can tell me in the comment area). gcc has not been installed before, so you can directly install version 9.4 without version management. The problem of soft link is mainly encountered during the installation of tbb library. Libtbb is required in the ORB program of SLAM so. 2, but only libtbb was created during installation So, so you can create one more.
The focus is on the writing of multithreaded programs. When traversing all feature points, multithreading is used to speed up. Add some knowledge about multithreading
for_each traverses the elements according to the iterator. Starting from C++17, the execution policy ExecutionPolicy is added. There are three kinds of policies:
- std::execution::seq enables the algorithm to execute in a deterministic order in a single thread, that is, not parallel and not concurrent;
- std::execution::par enables the algorithm to execute in multiple threads, and each thread has its own sequential tasks, that is, parallel but not concurrent;
- std::execution::par_unseq enables the algorithm to execute in multiple threads, and threads can have multiple concurrent tasks, that is, parallel and concurrent.
First and last are the start and end iterators respectively. The last one is function f (lambda expression is used in the program) and accepts the iterators in [first, last]. The function execution strategy can be selected from C++17. Here we use par_unseq (parallel and concurrent),
Need #include < execution >
The following locking part is very important. It was stuck for a while:
When calculating Angle, we don't need to worry about data conflict, because we use pointers for access, and the order doesn't matter. However, when calculating descriptors, we need to push the calculated descriptors_ Back to vector, which is a sequential container. Parallel and concurrency cannot guarantee push_ The order of back. In a multithreaded environment, there will be unpredictable errors in the insertion of shared resources. So need Lock protection , in C++11, < mutex > is added. We #include < mutex > and lock it( Reference here ), this is very important. Otherwise, the calculation descriptor can only be calculated in single thread seq. Finally, the core code of each part is shown in Listing 4, and the running result is shown in Figure 2.3. (I don't understand why it's slow to start computing multithreading, and then it's faster to call again. Is it because of the cache?)
void computeAngleMT(const cv::Mat &image, vector<cv::KeyPoint> &keypoints)
{
int half_patch_size = 8;
std::mutex m;
//or each is designed to traverse each one, so it can only be completed,
std::for_each(std::execution::par_unseq, keypoints.begin(), keypoints.end(),
[&half_patch_size, &image, &m](auto &kp)
{
// START YOUR CODE HERE
int u=kp.pt.x, v = kp.pt.y;
if(u>=half_patch_size && v>=half_patch_size && u+half_patch_size<=image.cols && v+half_patch_size<=image.rows)
{
float m01=0, m10=0;
for(int i=u-half_patch_size; i < u + half_patch_size; ++i) //Traverse 16 points in x direction (right)
for(int j=v-half_patch_size; j < v + half_patch_size; ++j) //Traverse 16 points in y direction (bottom)
{
m10 +=i * image.at<uchar>(j, i);
m01 +=j * image.at<uchar>(j, i);
}
std::lock_guard<std::mutex> guard(m);//Replace m.lock; m.unlock();
//Calculate the angle (in radians) and convert it to an angle
kp.angle = (float)std::atan(m01/m10) * 180/pi ; //Or std::atan2(m01, m10)*180/pi;
}
// END YOUR CODE HERE
});
return;
}
void computeORBDescMT(const cv::Mat &image, vector<cv::KeyPoint> &keypoints, vector<DescType> &desc)
{
// START YOUR CODE HERE (~20 lines)
std::mutex m;
std::for_each(std::execution::par_unseq, keypoints.begin(), keypoints.end(),
[&image, &desc, &m] (auto& kp) //lambda expression. This function accepts iterators
{
int u = kp.pt.x, v = kp.pt.y; //Iterators use - > to access members (combining dereference and member access)
DescType d(256, false); //256 bit descriptor
//STEP1: check whether the boundary is exceeded
if(u>=8 && v>=8 && u+8<=image.cols && v+8<=image.rows)
{
//STEP2: if it does not cross the boundary, collect the points according to the pattern, rotate the points P, q - > p',q', in combination with the directional angle theta of the feature points, calculate the coordinates of p',q', and compare the size. The result is the result of the bit descriptor (0 or 1)
for (int i = 0; i < 256; i++)
{
// START YOUR CODE HERE (~7 lines)
//Find the subscript of point pattern
cv::Point2f p(ORB_pattern[i * 4], ORB_pattern[i * 4 + 1]);
cv::Point2f q(ORB_pattern[i * 4 + 2], ORB_pattern[i * 4 + 3]);
//Using sin,cos, the angle is converted to radians * pi/180
double theta = kp.angle * pi / 180;
double cos_theta = cos(theta) , sin_theta = sin(theta);
int u_p_ = (int)(cos_theta * p.x - sin_theta * p.y) + u;
int v_p_ = (int)(sin_theta * p.x + cos_theta * p.y) + v;
int u_q_ = (int)(cos_theta * q.x - sin_theta * q.y) + u;
int v_q_ = (int)(sin_theta * q.x + cos_theta * q.y) + v;
//Judge whether the rotated p and q obtained according to the key point are out of bounds. If they are out of bounds, the descriptor is cleared and invalid
if(u_p_<0 || v_p_<0 || u_p_ >image.cols || v_p_ > image.rows || u_q_<0 || v_q_<0 || u_q_ >image.cols || v_q_ > image.rows)
{
d.clear();
// d = {};
break; //Jump out of descriptor loop
}
d[i] = image.at<uchar>(v_p_, u_p_) > image.at<uchar>(v_q_, u_q_) ? false : true; //The former takes false and the latter takes true. The vector random accessor is not fast enough, but mastering the algorithm is the key
}
}
//Do not use when crossing the boundary
else
{
d.clear();
// d = {};
}
std::lock_guard<std::mutex> guard(m);//Replace m.lock; m.unlock();
desc.push_back(d);
});
int bad_points = 0;
for(auto d:desc)
{
if(d.empty())
++bad_points;
}
cout << "Desc bad/total: " << bad_points << "/" << desc.size() << endl;
return;
// END YOUR CODE HERE
}
CMakeLists. Txt (don't forget the link tbb Library)
cmake_minimum_required(VERSION 3.21)
project(ORB_Extract)
set(CMAKE_CXX_STANDARD 17)
set(CMAKE_BUILD_TYPE "Release")
#set(CMAKE_BUILD_TYPE "Debug")
MESSAGE(STATUS "CMAKE_BUILD_TYPE IS ${CMAKE_BUILD_TYPE}")
find_package(OpenCV 3 REQUIRED)
#Add header file
include_directories(
${OpenCV_INCLUDE_DIRS}
${G2O_INCLUDE_DIRS}
${Sophus_INCLUDE_DIRS}
"/usr/local/include/eigen3/"
)
# Handwritten ORB features
add_executable(computeORB computeORB.cpp)
#Link OpenCV library and tbb Library
target_link_libraries(computeORB ${OpenCV_LIBS} tbb)
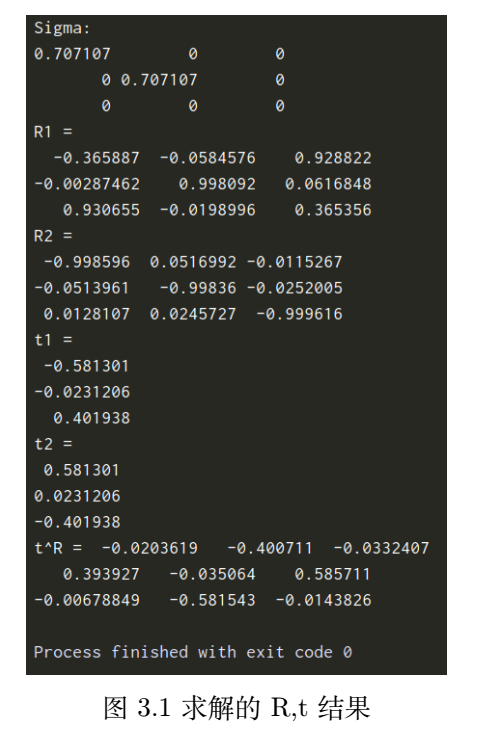
3. Recover R, t from E
There's nothing to say, but it's more impressive to write it once.
int main(int argc, char **argv) {
// Given Essential matrix
Matrix3d E;
E << -0.0203618550523477, -0.4007110038118445, -0.03324074249824097,
0.3939270778216369, -0.03506401846698079, 0.5857110303721015,
-0.006788487241438284, -0.5815434272915686, -0.01438258684486258;
// R,t to be calculated
Matrix3d R;
Vector3d t;
// SVD and fix sigular values
// START YOUR CODE HERE
// SVD on Sigma
Eigen::JacobiSVD<Eigen::Matrix3d> svd(E, Eigen::ComputeFullU | Eigen::ComputeFullV); //Eigen's svd function calculates the full rank U and V
Eigen::Matrix3d U = svd.matrixU();
Eigen::Matrix3d V = svd.matrixV();
Eigen::Vector3d sv = svd.singularValues();
cout << "U=" << U << endl;
cout << "V=" << V << endl;
cout << "sv=" << sv << endl;
Eigen::Matrix3d Sigma = Eigen::Matrix3d::Zero();
Sigma(0,0) = sv(0);
Sigma(1,1) = sv(1);
cout << "Sigma:\n" << Sigma << endl;
// END YOUR CODE HERE
// set t1, t2, R1, R2
// START YOUR CODE HERE
//use AngleAxis
Eigen::AngleAxisd rotation_vector_neg ( -M_PI/2, Eigen::Vector3d ( 0,0,1 ) ); //Rotate - 90 degrees along the Z axis
Eigen::AngleAxisd rotation_vector_pos ( M_PI/2, Eigen::Vector3d ( 0,0,1 ) ); //Rotate 90 degrees along the Z axis
Eigen::Matrix3d RzNegHalfPi = rotation_vector_neg.toRotationMatrix();
Eigen::Matrix3d RzPosHalfPi = rotation_vector_pos.toRotationMatrix();
Matrix3d t_wedge1 = U * RzPosHalfPi * Sigma * U.transpose();
Matrix3d t_wedge2 = U * RzNegHalfPi * Sigma * U.transpose();
Matrix3d R1 = U * RzPosHalfPi.transpose() * V.transpose();
Matrix3d R2 = U * RzNegHalfPi.transpose() * V.transpose();
// END YOUR CODE HERE
cout << "R1 = \n" << R1 << endl;
cout << "R2 = \n" << R2 << endl;
cout << "t1 = \n" << Sophus::SO3d::vee(t_wedge1) << endl; //Find Lie algebra??
cout << "t2 = \n" << Sophus::SO3d::vee(t_wedge2) << endl;
// check t^R=E up to scale
Matrix3d tR = t_wedge1 * R1;
cout << "t^R = " << tR << endl;
return 0;
}
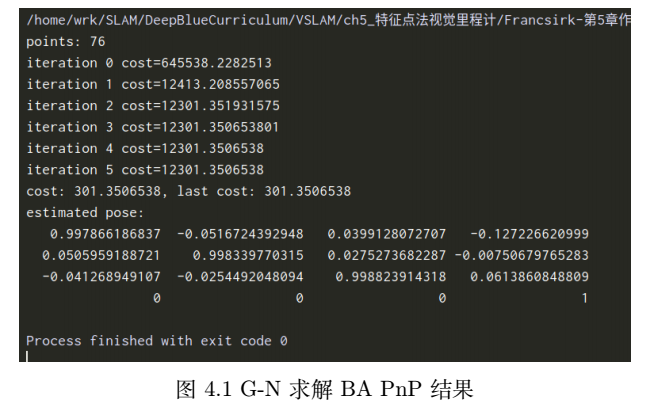
4. Use G-N to realize pose estimation in Bundle Adjustment
int main(int argc, char **argv)
{
VecVector2d p2d;
VecVector3d p3d;
Matrix3d K;
double fx = 520.9, fy = 521.0, cx = 325.1, cy = 249.7;
K << fx, 0, cx, 0, fy, cy, 0, 0, 1;
// load points in to p3d and p2d
// START YOUR CODE HERE
double data2d[2] = {0}, data3d[3] = {0};
ifstream fin2d(p2d_file), fin3d(p3d_file);
for(int i=0;i<76;++i)
{
fin2d>>data2d[0];
fin2d>>data2d[1];
p2d.push_back(Eigen::Vector2d(data2d[0], data2d[1]));
fin3d>>data3d[0];
fin3d>>data3d[1];
fin3d>>data3d[2];
p3d.push_back(Eigen::Vector3d(data3d[0], data3d[1], data3d[2]));
}
// END YOUR CODE HERE
assert(p3d.size() == p2d.size());
int iterations = 100;
double cost = 0, lastCost = 0;
int nPoints = p3d.size();
cout << "points: " << nPoints << endl;
Sophus::SE3d T_esti; // Lie group, not lie algebra, Lie algebra is se3, Vector3d
for (int iter = 0; iter < iterations; iter++) {
Matrix<double, 6, 6> H = Matrix<double, 6, 6>::Zero();
Vector6d b = Vector6d::Zero();
cost = 0;
// compute cost calculation error is observation prediction
for (int i = 0; i < nPoints; i++)
{
// compute cost for p3d[I] and p2d[I]
// START YOUR CODE HERE
Eigen::Vector3d pc = T_esti * p3d[i]; //3D points are converted to the camera coordinate system (the first three dimensions are taken)
double inv_z = 1.0 / pc[2];
double inv_z2 = inv_z * inv_z;
Eigen::Vector2d proj(fx * pc[0] / pc[2] + cx, fy * pc[1] / pc[2] + cy); //Re projection, prediction
Eigen::Vector2d e = p2d[i] - proj;
cost += e.transpose() * e;
// END YOUR CODE HERE
// compute jacobian
Matrix<double, 2, 6> J;
// START YOUR CODE HERE
J<<fx * inv_z,
0,
-fx * pc[0] * inv_z2,
-fx * pc[0] * pc[1] * inv_z2,
fx + fx * pc[0] * pc[0] * inv_z2,
-fx * pc[1] * inv_z,
0,
fy * inv_z,
-fy * pc[1] * inv_z2,
-fy - fy * pc[1] * pc[1] * inv_z2,
fy * pc[0] * pc[1] * inv_z2,
fy * pc[0] * inv_z;
J = -J;
// END YOUR CODE HERE
//Coefficient matrix and nonhomogeneous term of Gauss Newton
H += J.transpose() * J;
b += -J.transpose() * e;
}
// solve dx
Vector6d dx; //The solution of △ x is a lie algebra
// START YOUR CODE HERE
dx = H.ldlt().solve(b); //solve equations
// END YOUR CODE HERE
if (isnan(dx[0]))
{
cout << "result is nan!" << endl;
break;
}
if (iter > 0 && cost >= lastCost) {
// cost increase, update is not good
cout << "cost: " << cost << ", last cost: " << lastCost << endl;
break;
}
// update your estimation
// START YOUR CODE HERE
T_esti = Sophus::SE3d::exp(dx) * T_esti;
// END YOUR CODE HERE
lastCost = cost;
cout << "iteration " << iter << " cost=" << cout.precision(12) << cost << endl;
}
cout << "estimated pose: \n" << T_esti.matrix() << endl;
return 0;
}
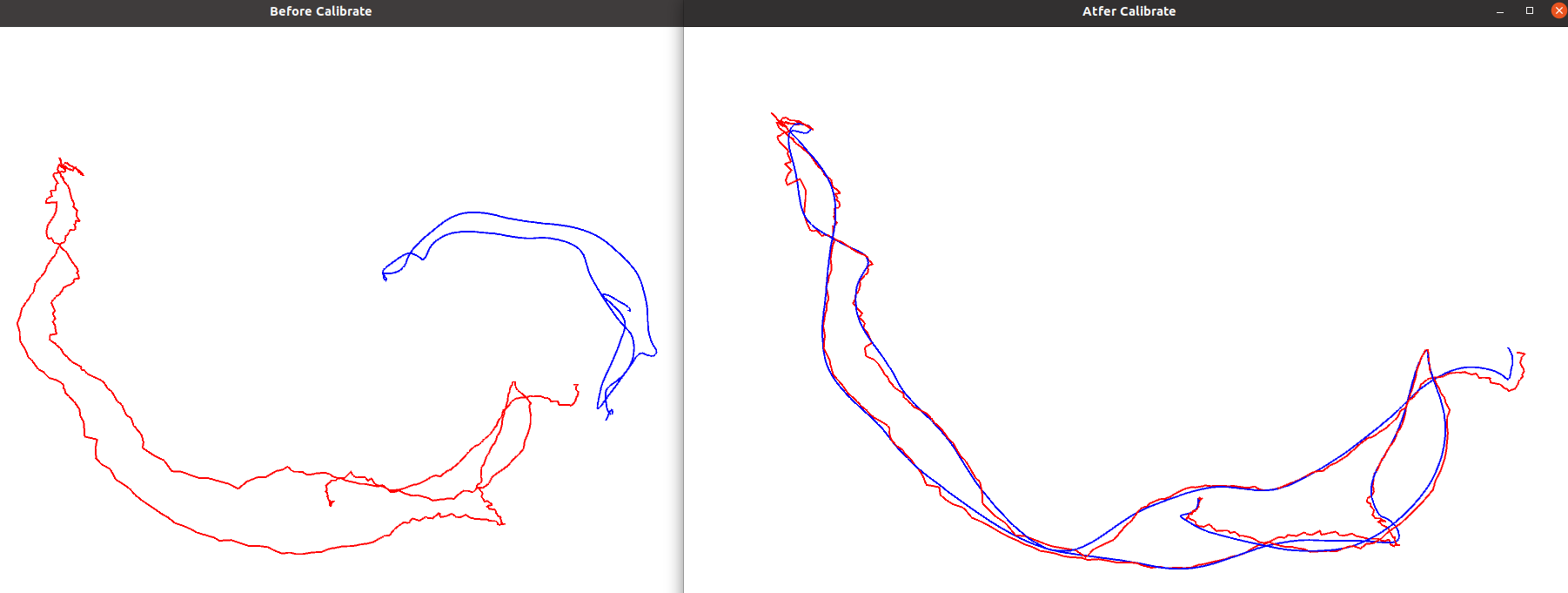
5. Track alignment using ICP
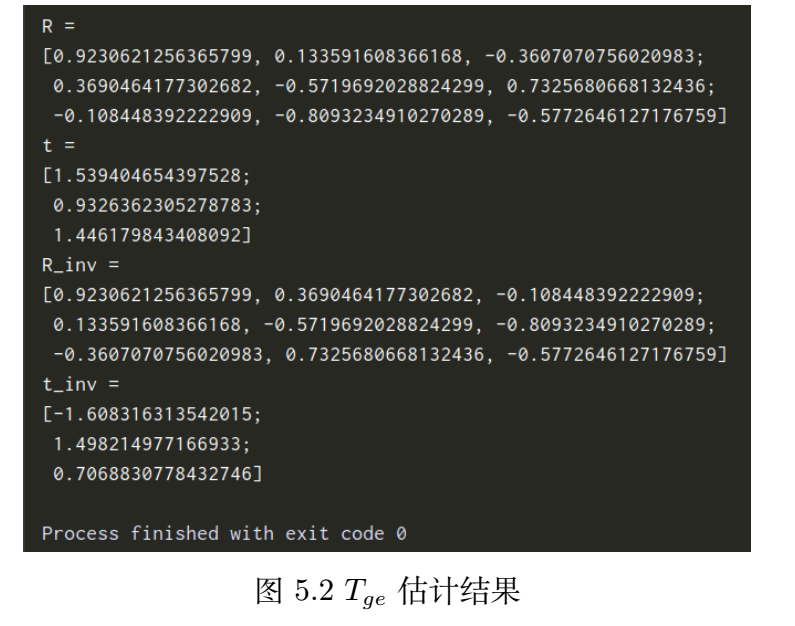
Use the track drawing and reading code in Chapter 3 to modify, add the program of handwritten ICP part, and finally track output and T g e T_{ge} The estimation result of Tge ^ is shown in the figure, and the code of the core part is shown below.
Thinking: I want to calculate the RMSE of the two trajectories, but after thinking, I find that the translation part is regarded as the position P, then the two trajectories are equivalent to two frames of images, and there is only one pose transformation T between them, and the calculation of RMSE is to calculate the error of all T on the whole track, so calculate T g e T_{ge} Tge # back pair T e T_e Te , and RMSE can be calculated.
#include <iostream>
#include <fstream>
#include <unistd.h>
#include <pangolin/pangolin.h>
#include <sophus/se3.hpp>
#include <opencv2/core/core.hpp>
using namespace Sophus;
using namespace std;
using namespace cv;
string compare_file = "./compare.txt";
typedef vector<Sophus::SE3d, Eigen::aligned_allocator<Sophus::SE3d>> TrajectoryType;
typedef vector<TrajectoryType> LongTrajectoryType;
typedef Eigen::Matrix<double,6,1> Vector6d;
void DrawTrajectory(const vector<Point3d> >, const vector<Point3d> &esti, const string& title);
vector<TrajectoryType> ReadTrajectory(const string &path);
vector<Point3d> GetPoint(TrajectoryType TT);
void pose_estimation_3d3d(const vector<Point3d> &pts1, const vector<Point3d> &pts2, Mat &R, Mat &t);
vector<Point3d> TrajectoryTransform(Mat T, Mat t, vector<Point3d> esti );
int main(int argc, char **argv) {
LongTrajectoryType CompareData = ReadTrajectory(compare_file);
assert(!CompareData.empty());
cout<<"size: "<<CompareData.size()<<endl;
vector<Point3d> EstiPt = GetPoint(CompareData[0]);
vector<Point3d> GtPt = GetPoint(CompareData[1]);
Mat R, t; //Pose to be found
pose_estimation_3d3d( GtPt, EstiPt, R, t);
cout << "ICP via SVD results: \n" << endl;
cout << "R = \n" << R << endl;
cout << "t = \n" << t << endl;
cout << "R_inv = \n" << R.t() << endl;
cout << "t_inv = \n" << -R.t() * t << endl;
DrawTrajectory(GtPt, EstiPt, "Before Calibrate");
vector<Point3d> EstiCali = TrajectoryTransform(R, t, EstiPt);
DrawTrajectory(GtPt, EstiCali, "Atfer Calibrate");
return 0;
}
LongTrajectoryType ReadTrajectory(const string &path)
{
ifstream fin(path);
TrajectoryType trajectory1, trajectory2;
if (!fin) {
cerr << "trajectory " << path << " not found." << endl;
return {};
}
while (!fin.eof()) {
double time1, tx1, ty1, tz1, qx1, qy1, qz1, qw1;
fin >> time1 >> tx1 >> ty1 >> tz1 >> qx1 >> qy1 >> qz1 >> qw1;
double time2, tx2, ty2, tz2, qx2, qy2, qz2, qw2;
fin >> time2 >> tx2 >> ty2 >> tz2 >> qx2 >> qy2 >> qz2 >> qw2;
Sophus::SE3d p1(Eigen::Quaterniond(qw1, qx1, qy1, qz1), Eigen::Vector3d(tx1, ty1, tz1));
trajectory1.push_back(p1);
Sophus::SE3d p2(Eigen::Quaterniond(qw2, qx2, qy2, qz2), Eigen::Vector3d(tx2, ty2, tz2));
trajectory2.push_back(p2);
}
LongTrajectoryType ret{trajectory1, trajectory2};
return ret;
}
void DrawTrajectory(const vector<Point3d> >, const vector<Point3d> &esti, const string& title)
{
// create pangolin window and plot the trajectory
pangolin::CreateWindowAndBind(title, 1024, 768);
glEnable(GL_DEPTH_TEST);
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
pangolin::OpenGlRenderState s_cam(
pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
);
pangolin::View &d_cam = pangolin::CreateDisplay()
.SetBounds(0.0, 1.0, pangolin::Attach::Pix(175), 1.0, -1024.0f / 768.0f)
.SetHandler(new pangolin::Handler3D(s_cam));
while (pangolin::ShouldQuit() == false) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
d_cam.Activate(s_cam);
glClearColor(1.0f, 1.0f, 1.0f, 1.0f);
glLineWidth(2);
for (size_t i = 0; i < gt.size() - 1; i++) {
glColor3f(0.0f, 0.0f, 1.0f); // blue for ground truth
glBegin(GL_LINES);
auto p1 = gt[i], p2 = gt[i + 1];
glVertex3d(p1.x, p1.y, p1.z);
glVertex3d(p2.x, p2.y, p2.z);
glEnd();
}
for (size_t i = 0; i < esti.size() - 1; i++) {
glColor3f(1.0f, 0.0f, 0.0f); // red for estimated
glBegin(GL_LINES);
auto p1 = esti[i], p2 = esti[i + 1];
glVertex3d(p1.x, p1.y, p1.z);
glVertex3d(p2.x, p2.y, p2.z);
glEnd();
}
pangolin::FinishFrame();
usleep(5000); // sleep 5 ms
}
}
void pose_estimation_3d3d(const vector<Point3d> &pts1,
const vector<Point3d> &pts2,
Mat &R, Mat &t) {
Point3d p1, p2; // center of mass, where p1 represents the first picture and p2 represents the second picture, which is opposite to R in the book, so R21 = R12^(-1)=R12^(T), and finally output
int N = pts1.size();
for (int i = 0; i < N; i++) {
p1 += pts1[i];
p2 += pts2[i];
}
p1 = Point3d(Vec3d(p1) / N);
p2 = Point3d(Vec3d(p2) / N);
vector<Point3d> q1(N), q2(N); // remove the center
for (int i = 0; i < N; i++) {
q1[i] = pts1[i] - p1;
q2[i] = pts2[i] - p2;
}
// compute q1*q2^T
Eigen::Matrix3d W = Eigen::Matrix3d::Zero();
for (int i = 0; i < N; i++)
{
W += Eigen::Vector3d(q1[i].x, q1[i].y, q1[i].z) * Eigen::Vector3d(q2[i].x, q2[i].y, q2[i].z).transpose(); //Here is 2 - > 1 R12, and R21 needs to be transposed
}
cout << "W= \n" << W << endl;
// SVD on W
Eigen::JacobiSVD<Eigen::Matrix3d> svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV); //Eigen's svd function calculates the full rank U and V
Eigen::Matrix3d U = svd.matrixU();
Eigen::Matrix3d V = svd.matrixV();
cout << "U= \n" << U << endl;
cout << "V= \n" << V << endl;
Eigen::Matrix3d R_ = U * (V.transpose()); //Can we guarantee that det(R)=1 and orthogonal?
cout<<"My output: det(R_): "<<R_.determinant()<<"\nR_: \n"<<R_<<endl; //Eigen's Mat
if (R_.determinant() < 0) //If the determinant is negative, take - R
{
R_ = -R_;
}
Eigen::Vector3d t_ = Eigen::Vector3d(p1.x, p1.y, p1.z) - R_ * Eigen::Vector3d(p2.x, p2.y, p2.z); //Optimal t=p-Rp '
// convert to cv::Mat
R = (Mat_<double>(3, 3) <<
R_(0, 0), R_(0, 1), R_(0, 2),
R_(1, 0), R_(1, 1), R_(1, 2),
R_(2, 0), R_(2, 1), R_(2, 2)
);
t = (Mat_<double>(3, 1) << t_(0, 0), t_(1, 0), t_(2, 0));
}
vector<Point3d> GetPoint(TrajectoryType TT)
{
vector<Point3d> pts;
for(auto each:TT)
//There is no need to deal with the camera model, nor / 5000
pts.push_back(Point3d(each.translation()[0], each.translation()[1], each.translation()[2]));
return pts;
}
//transformation
vector<Point3d> TrajectoryTransform(Mat T, Mat t, vector<Point3d> esti )
{
vector<Point3d> calibrated={};
Mat Mat__31;
Sophus::SE3d SE3D;
for(auto each:esti)
{
Mat__31 = (Mat_<double>(3, 1)<<each.x, each.y, each.z);
Mat__31 = T * Mat__31 + t;
calibrated.push_back( Point3d(Mat__31));
}
return calibrated;
}
Then catch up!