littlejunk is too painful. I've been doing it for a day and a half under the careful tips of my seniors. The clown is myself. Even if ida bullies me, dev gives me a bug.
RE
1. py check in
After unpacking the classic python packaged exe program, the pyinstxtracker fixes the file header of the non suffix file named py, and then decompiles the source code directly with uncompyle6.
def encode(s):
str = ''
for i in range(len(s)):
res = ord(s[i]) ^ 32
res += 31
str += chr(res)
return str
m = 'ek`fz13b3c5e047b`bd`0/c268e600e7c5d1`|'
strings = ''
strings = input('Input:')
if encode(strings) == m:
print 'Correct!'
else:
print 'Try again!'
# okay decompiling py.pyc
Simple inverse operation is enough
m='ek`fz13b3c5e047b`bd`0/c268e600e7c5d1`|' for i in range(len(m)): print(chr((ord(m[i])-31)^32),end='')
2,apkre
Android reverse problem, I will find common ideas at present. Get the apk file, unzip it directly, and find the class DEX file, using d2j-dex2jar Bat decompiles DEX into jar files, and then uses JD GUI to view the source code. Android killer is a little slow
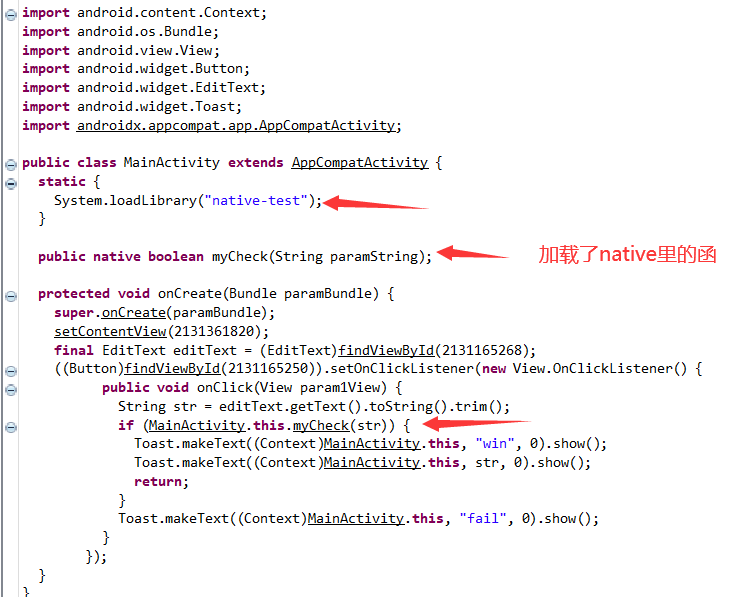The reverse of the native layer is mainly a mycheck function to check.
Go to the lib folder to find the so file under x86, directly drag it into ida, search for mycheck in the function window, and you can locate it. Looking at the decompiled code, you can also know that the flag is 32 bits.
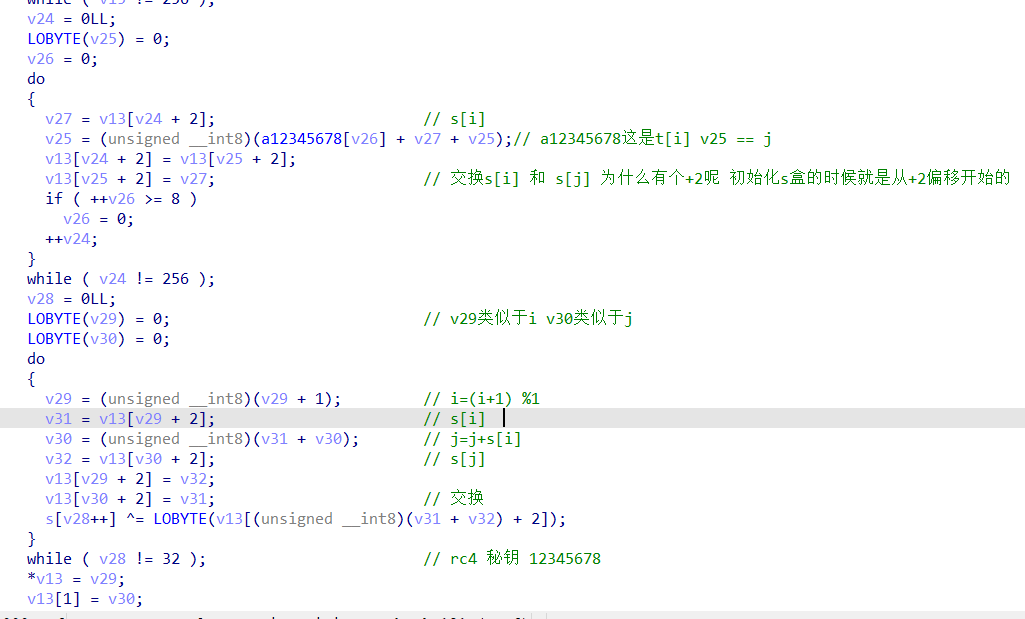
When initializing the s-box, there are many sse instructions, which can be learned later. However, at that time, we saw something similar to rc4, and then the secret key has clear text, so we can directly set a script. But the online website is a little fragrant, hand speed questions.
summary
Android reverse now knows a little. I also need to understand the structure and common reverse ideas. It's faster to debug the outflow secret key for this problem. At present, I'm not very good at it.
3,littlejunk
① Dynamic and static analysis
I didn't do it during the competition. I simply thought it was a Tea encryption. Finally, key made a mistake, but there were still many holes in this problem. It took me a day and a half to figure it out under the careful prompt of my hero.
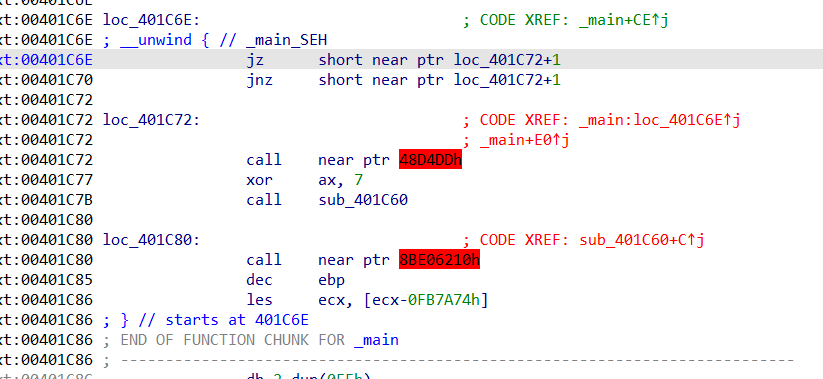First, there are two flower instructions in the main function. It is a common type. Because it jumps to a label + 1, the first byte at the label always does not work, so it can be nop dropped.
Then a suspicious place is found, with the word ctf, and function 1 performs an XOR operation on the bytes at an address.
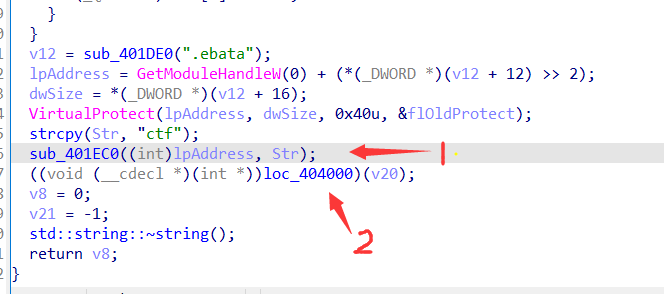
Function 1
According to the experience of doing problems, this is to cover up the content of the function through XOR. Only when you move here can you see the original appearance of the function. Listen to the senior students say that this is an smc, self modification technology. I don't know much. Don't scold. It's too lazy.
So we're going to move here and let him XOR himself and look at the content of the function after XOR.
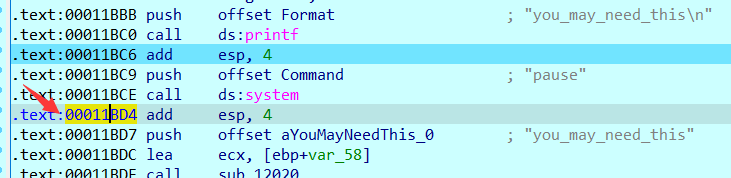Of course, if you directly adjust, there will be a system function, which is considered to be a relatively low anti debugging. At the next breakpoint, modify the eip to the place pointed by the arrow, or the beginning of other statements. Don't rewrite the middle randomly, and ida will collapse.
Of course, the next breakpoint near the function to be observed bypasses the system and goes directly to F9.
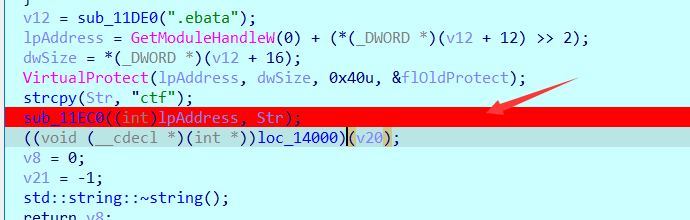
Through debugging, it is found that this ipAddress points to LOC_ The first byte of the 14000 function, as guessed, is the modified function below.
Before modification: nothing, don't mess nop.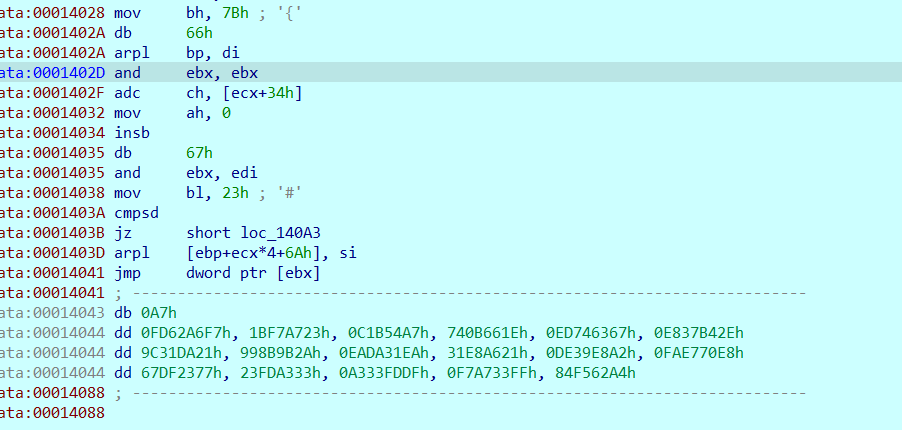
After F8 single step, go in and turn the data into code according to C, and then p change this function again.
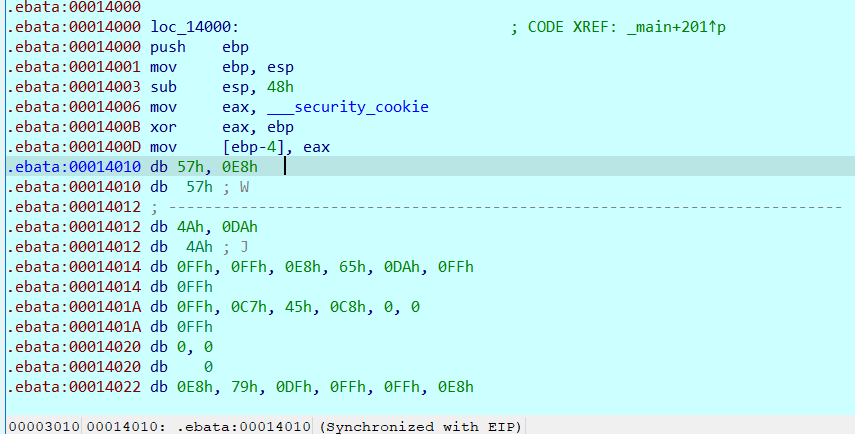
The code is put in the non code segment. It's scary to see you for the first time.
It should be noted here that there is no flower instruction in this function. It is all useful code. It may not be able to directly C. if C does not move, press u for analysis first, or d to convert data, and then press c!!!
At the beginning, I couldn't c all nop here. As a result, I became more and more fascinated.
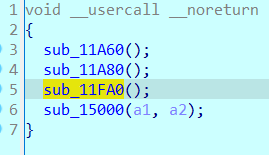
At the beginning, it was a little strange. It will be solved later. Follow in one step to see what the situation is.
Click the first and second functions to have a look. print lets you enter flag, and then enter flag. The flag must be 38 bits, and then the format is flag {}
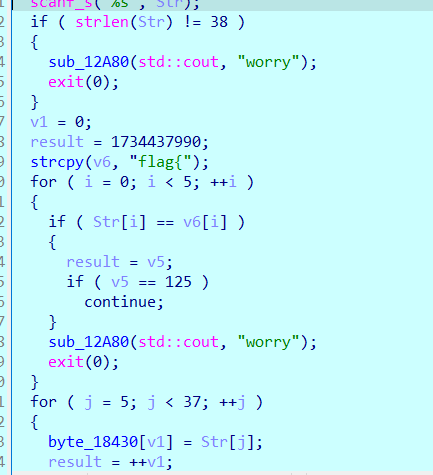
Use python to construct a flag, which is also convenient for tracking and calculation.
flag {aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
After the next function follows up, it is a self decryption function. The strange structure is related to here. This is luck. Buy one get one free. Hurry to buy lottery tickets.
After completing this self modifying function step by step, enter the fourth function, which is quite fancy. The assembly window is sorted according to u+c.
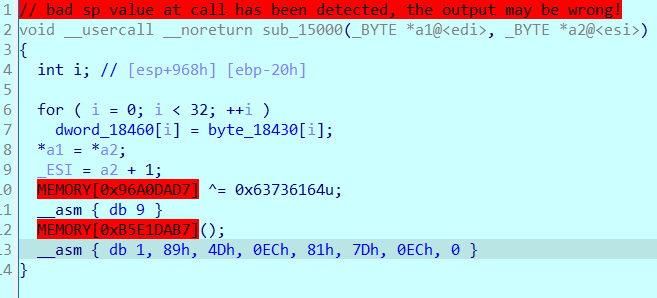
After finishing: pay attention to redefine the function p, and there is no flower instruction
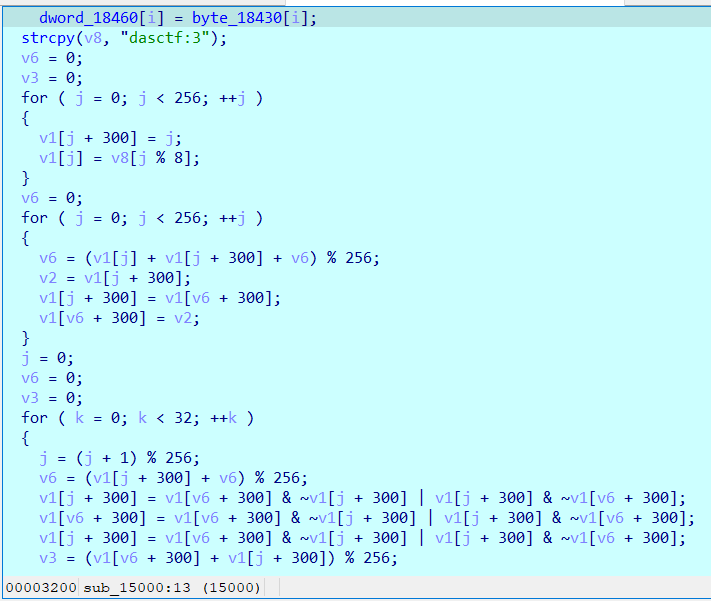A function similar to RC4, but the final algorithm is strange.
Then I went outside. After F5, a red instruction appeared, which is the part that has appeared since the modification. The assembly window table followed up and continued to sort it out.
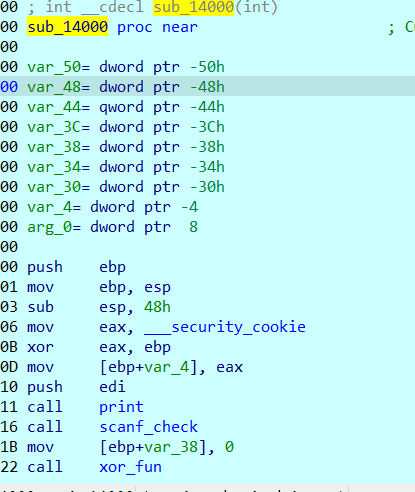
Mainly in sub_ In the 14000 function label, click u or d and then p until the above figure is normal. Prompt again, there is no flower instruction!!! Look at the title, little, just a little ~.
This is the 1400 function. I changed the function name, that is, first enter flag, and then perform an encryption similar to rc4. Anyway, it is XOR. Just call out the key.
Press F8 directly and take a look at the global variable of rc4 return. There is also a pit!!! I don't know which one it is.
It's very silly to go in and see that the processed string has become one. Note that there is an align100 below. Click u.
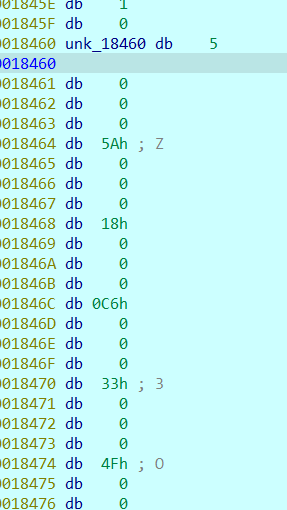
There are 32 in total. Each takes the first byte. Here, 5 is actually a high byte, but the function to enlarge the end order puts 5 in the fourth address, that is, it becomes a low byte. The 32 data obtained here are key[i] ^ord('a '). You can get the key of rc4 after XOR.
Then there is the last function, which is also messy. Here are two flower instructions, which are the same as the principle of the main function.
No more explanation, just change it yourself. Pay attention to redefine the function after modification.
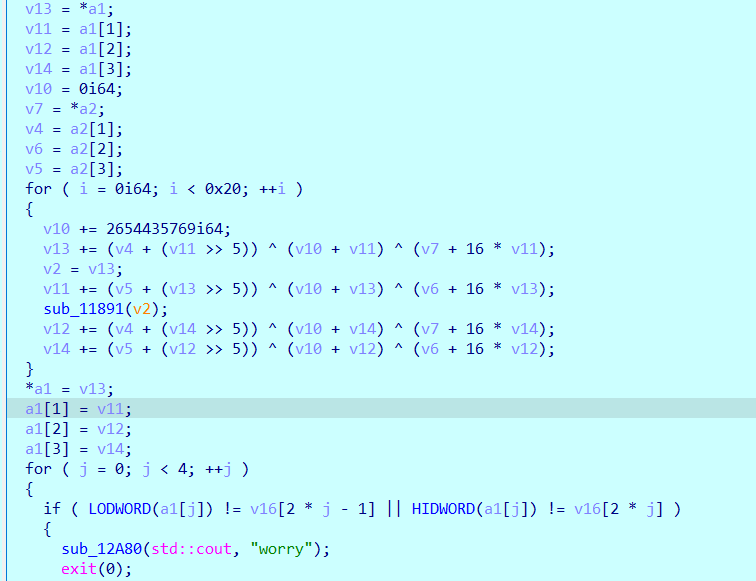Tea encryption, evolutionary version. It can be seen that v13 and v11 are a group, v12 and v14 are a group, and the delta is 0x9E3779B9. However, the original tea encryption is two 4-byte plaintext and four 4-byte secret key. This is two 8 bytes of plaintext and written in a loop. The secret key has four 8 bytes, which I would like to call giant tea.
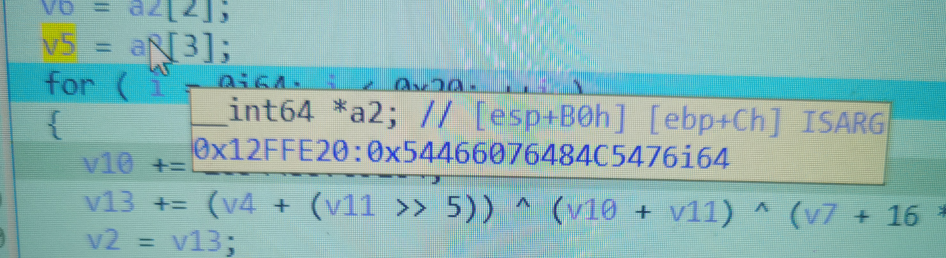
When you move to a2, you can see the address of a2, 0x12ffe20, and find this address in hex window G.
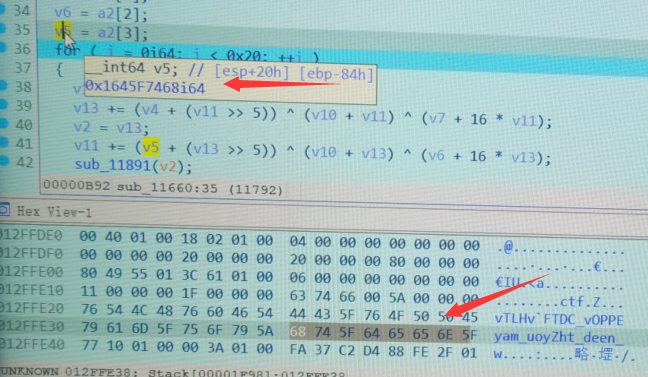
In order to prove ida's deception, the mobile phone took evidence. The real secret key is four 8 bytes starting from 0x12ffe20. Note that the small end order should be changed to the correct order, and the key extracted from the memory is the real key.
0x54466076484c5476 , 0x4550504f765f4344 , 0x5a796f755f6d6179 , 0x5f6e6565645f7468
This is the ciphertext and the final check. However, the final comparison of his 256bit Tea encryption is that the first number is low and the second number is high. In pairs, you can spell out the four most encrypted values, and then decrypt them in pairs.
② The bitter experience of writing scripts
#include<iostream>
#include<iomanip>
#include<cstring>
using namespace std;
void tea_decode(unsigned __int64*s,unsigned __int64 *key);
int main(){
unsigned __int64 m[2]={0x2FDE61CCEFC70FF8,0x56BC19E119C8B07B};
//Group I: 0xE990A522BE80F786
unsigned __int64 key[4]={0x54466076484c5476 , 0x4550504f765f4344 , 0x5a796f755f6d6179 , 0x5f6e6565645f7468};
tea_decode(m,key);
unsigned long long a=0x9e3779b9L * 0x20L;//test
cout<<hex<<a<<endl; //test
return 0;
}
void tea_decode(unsigned __int64 *s,unsigned __int64 *key){
unsigned __int64 v0=s[0];
unsigned __int64 v1=s[1];
unsigned __int64 sum=0x13c6ef3720; // The 0x9e3779b9*0x20 devc only reserves the lower four bytes for me
unsigned __int64 defalt=0x9e3779b9;
unsigned __int64 k0=key[0],k1=key[1],k2=key[2],k3=key[3];
for(int i=0;i<0x20;i++){
v1-=((v0<<4)+k2)^(v0+sum)^((v0>>5)+k3);
v0-=((v1<<4)+k0)^(v1+sum)^((v1>>5)+k1);
sum-=defalt;
}
s[0]=v0;
s[1]=v1;
cout<<v0<<","<<v1<<endl;
}
Note: during Tea decryption, the sum directly writes the calculated result 0x13c6ef3720, not 0x9e3779b9*0x20. If the result of the second writing method only keeps the lower 32bit, even if you open up the size of 8 bytes, there will still be this pit.
Stream cipher decryption after Tea decryption
from Crypto.Util.number import *
#print('flag{'+'a'*32+'}')
a=[ 0x05, 0x00, 0x00, 0x00, 0x5A, 0x00, 0x00, 0x00, 0x18, 0x00,
0x00, 0x00, 0xC6, 0x00, 0x00, 0x00, 0x33, 0x00, 0x00, 0x00,
0x4F, 0x00, 0x00, 0x00, 0xCE, 0x00, 0x00, 0x00, 0x83, 0x00,
0x00, 0x00, 0x57, 0x00, 0x00, 0x00, 0xAC, 0x00, 0x00, 0x00,
0xF3, 0x00, 0x00, 0x00, 0x3D, 0x00, 0x00, 0x00, 0x7F, 0x00,
0x00, 0x00, 0x0B, 0x00, 0x00, 0x00, 0x24, 0x00, 0x00, 0x00,
0x05, 0x00, 0x00, 0x00, 0x6C, 0x00, 0x00, 0x00, 0x60, 0x00,
0x00, 0x00, 0x0E, 0x00, 0x00, 0x00, 0xD3, 0x00, 0x00, 0x00,
0x1F, 0x00, 0x00, 0x00, 0xA5, 0x00, 0x00, 0x00, 0xFA, 0x00,
0x00, 0x00, 0xEB, 0x00, 0x00, 0x00, 0x59, 0x00, 0x00, 0x00,
0x63, 0x00, 0x00, 0x00, 0x38, 0x00, 0x00, 0x00, 0x0F, 0x00,
0x00, 0x00, 0xF6, 0x00, 0x00, 0x00, 0x17, 0x00, 0x00, 0x00,
0x42, 0x00, 0x00, 0x00, 0xA5, 0x00, 0x00, 0x00]
key=[]
for i in range(len(a)//4):
key.append(a[4*i]^97)
#dump the key of rc4
#After tea decryption
cc1=[5790024677284421248,265414871944557825,3760601914643164344,675928458074199027]
temp=int.to_bytes(cc1[0],8,byteorder='big') #It has helped us turn the small end into the big end. We are not allowed to change it by ourselves
temp+=int.to_bytes(cc1[1],8,byteorder='big')
temp+=int.to_bytes(cc1[2],8,byteorder='big')
temp+=int.to_bytes(cc1[3],8,byteorder='big')
for i in range(len(temp)):
print(chr(temp[i]^key[i]),end='')
#flag{4a5c0f1b5cc7f60e918611721c87ba07}
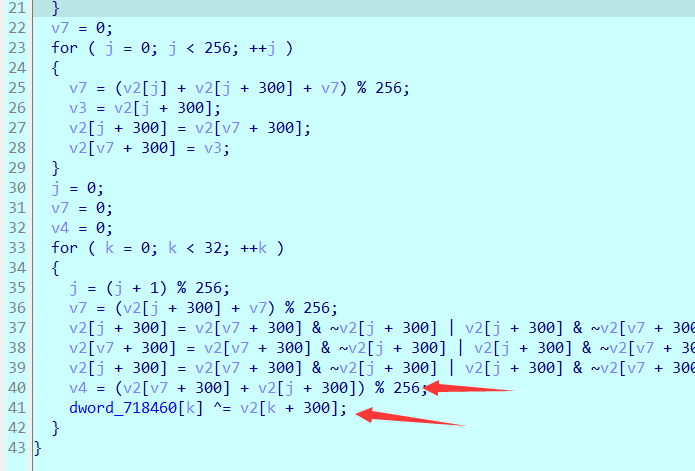
In contrast, this rc4 is actually a trick. The original version of v4 should be s[v4]^m[i], but it is m[i]^s[i]. The three steps in the middle are still exchange functions, as shown in the python example below.
def fun(a,b):
a = b & ~a | a & ~b
b = b & ~a | a & ~b
a = b & ~a | a & ~b
print(a,b)
fun(3,4) -> 4 3
Of course, for the stream cipher, the dynamic adjustment can quickly decrypt the stream secret key.
Summary:
In fact, it's not so complicated to repeat it. There are only 4 instructions and 2 self decryption algorithms. Finally, there is an rc4 and a huge TEA. In fact, it's not so clear at the beginning of the question. You can see a lot of information directly by looking at the string window. You can set breakpoints in those places. Of course, it's funny to deduct a score question for so long, But I also learned a lot of details, such as symbol processing, devc bug s, self decryption, etc. in my idol's words, don't always think about the set. Learn more. 10 minutes is a solid foundation. haha, climb slowly!
Crypto
The overall difficulty is small. The theme of this issue is the reproduction of the competition question, but it is also very interesting
1,easymath
The original question can be found directly by Google. It has also been done in school competitions before. It is mainly to find the inverse yuan.
assert(len(open('flag.txt', 'rb').read()) < 50)
assert(str(int.from_bytes(open('flag.txt', 'rb').read(), byteorder='big') << 10000).endswith(
'1862790884563160582365888530869690397667546628710795031544304378154769559410473276482265448754388655981091313419549689169381115573539422545933044902527020209259938095466283008'))
The endwith function determines whether to end with the specified string, that is, the tail is the content in parentheses, which is 175 digits.
Namely
c = (flag<<10000)%(10^175) Shift 10000 to the left, that is, multiply by 2**10000 Power primitive c = flag*(2**10000) % 10^175 If 2**10000 At 10^175 Lower inverse element It can be solved directly flag，But 2**10000 And 10^175 Not mutually prime, but with 5^175 Mutual prime, and 10^175 It's five^175 Multiple of, so (c%(10^175)) again%5^175 And direct c%(5^175)The value of is the same.
Directly find an inverse element and get the flag
import gmpy2 from Crypto.Util.number import * d=gmpy2.invert(2**10000,5**175) c=... f=long_to_bytes(c*d%(5**175)) print(f)
2,let's play with rsa~
from sympy import isprime,nextprime
from Crypto.Util.number import getPrime as getprime ,long_to_bytes,bytes_to_long,inverse
flag='flag{***************}'
def play():
p=getprime(1024)
q=getprime(1024)
n=p*q
e=65537
print "Hello,let's play rsa~\n"
print 'Now,I make some numbers,wait a second\n'
n1=getprime(200)
n2=getprime(200)
number=n1*n2
print "Ok,i will send two numbers to you,one of them was encoded.\n"
print "Encode n1:%d,\n"%(pow(n1,e,n))
print "And n2:%d.\n"%n2
print "Information that can now be made public:the public key (n,e):(%d,%d)\n"%(n,e)
while True:
try:
c=int(raw_input("ok,now,tell me the value of the number (encode it for safe):"))
except:
print "Sorry,the input is illeagal, and the integer is accept~"
else:
break
d=inverse(e,(p-1)*(q-1))
m=pow(c,d,n)
if m==number:
print "It's easy and interesting,didn't it?\n"
print "This is the gift for you :"+flag
else:
print "Emmmmm,there is something wrong, bye~\n"
if __name__ == '__main__':
play()
Wuhu, it happens that Samsung's ctf tutorial is about this attack. The general process is e and N. then he produces n1, n2, number=n1*n2. We get (pow(n1,e,n)) and n2. Then let's turn to a number, and he decrypts m=pow(c,d,n) and check s with number.
((n1^e)%n * (n2^e)%n)%n =(n1*n2)^e %n = number^e %n #It is the formula of multiplication with modular operation, (n1^e)%n n2 has been known and can be constructed directly print((pow(n2,e,n)*n1)%n) nc Connect and upload to get flag
summary
Sometimes, the server may restrict our input. For example, a hello is sent in, which is an rsa encryption mechanism, and will be automatically encrypted and decrypted. He requires us to decrypt the incoming ciphertext and add it equal to Hello, and he will give us a flag.
However, when we directly pass in hello for encryption, he adds this input. At this time, we can convert Hello into a numerical value and factorize it, that is, m1*m2==m. then we pass in m1 and M2, and the system will return pow(m1,e,n) and pow(m2,e,n), and then% n the product of the two, so as to construct the ciphertext of Hello, After that, you can get the flag.
3,ezRSA
from secret import flag
from Crypto.Util.number import *
from random import getrandbits
from hashlib import sha256
class EzRsa:
def __init__(self):
self.E = 0x10001
self.P = getPrime(1024)
self.Q = getPrime(1024)
while GCD((self.P-1)*(self.Q-1), self.E) != 1:
self.Q = getPrime(1024)
self.N = self.P*self.Q
def encrypt(self):
f = getrandbits(32)
c = pow(f, self.E, self.N)
return (f, c)
def encrypt_flag(self, flag):
f = bytes_to_long(flag)
c = pow(f, self.E, self.N)
return c
def proof():
seed = getrandbits(32)
print(seed)
sha = sha256(str(seed).encode()).hexdigest()
print(f"sha256({seed>>18}...).hexdigest() = {sha}")
sha_i = input("plz enter seed: ")
if sha256(sha_i.encode()).hexdigest() != sha:
exit(0)
if __name__ == "__main__":
proof()
print("welcome to EzRsa")
print("""
1. Get flag
2. Encrypt
3. Insert
4. Exit
""")
A = EzRsa()
coin = 5
while coin > 0:
choose = input("> ")
if choose == "1":
print(
f"pow(flag,e,n) = {A.encrypt_flag(flag)}\ne = 0x10001")
exit(0)
elif choose == "2":
f, c = A.encrypt()
print(f"plain = {f}\ncipher = {c}")
coin -= 1
elif choose == "3":
q = getrandbits(1024)
n = A.P*q
f = getrandbits(32)
c = pow(f, 0x10001, n)
print(f"plain = {f}\ncipher = {c}")
coin -= 1
elif choose == "4":
print("bye~")
else:
print("wrong input")
print("Now you get the flag right?")
The check of the first sha256 is a little outrageous. The seed is given. Just copy and paste it directly.
The initial value of coin is 5, and each selection will be - 1, which can be cycled up to 5 times.
If you choose 1, you will get the ciphertext of flag, but if you choose 1, you will exit.
Select 2 to give you plaintext and encrypted ciphertext, and e to 0x10001
If you choose 3, you also give a set of plaintext and ciphertext. e is 0x10001, but n is different from 2. Here n is the extracted P multiplied by a random number.
... who will choose 4???
According to 2, by m^e=c+k*n (m^e -c =k*n) If you get two sets of 2, you can leak by finding the common factor k*n Similarly, according to m^e -c =k*P*q You can get it by taking the common factor k*q Note that this is generally k*n perhaps k*q k It can be blasted in a small range. After all, the plaintext is relatively short, n Relatively large So we just need to take two groups of two to leak n，Take two sets of 3 to leak P Can decompose n，Then decrypt normally rsa Yes
Decryption script
import gmpy2
from Crypto.Util.number import *
from random import getrandbits
e= 0x10001
p1=1751297511
c1=
p2=3438100521
c2=
#The above data is used for leakage. n is taken 2 times continuously
p3=1584259449
c3=
p4=3829043104
c4=
#Leakage p is taken twice in succession
enc=
n=gmpy2.gcd(pow(p1,e)-c1,pow(p2,e)-c2) #Maybe k of k*n also has a common factor, which can be reduced in a small range
#for i in range(2,100):
# if n%i==0:
# print(i)
n=n//22 #i find 22
p=gmpy2.gcd(pow(p3,e)-c3,pow(p4,e)-c4) #Because q of 3 is random, the common factor is k*q
#for i in range(2,100):
# if p%i==0:
# print(i)
p=p//3
#if n%p==0:
# print('yes')
q=n//p
d=gmpy2.invert(e,(p-1)*(q-1))
print(long_to_bytes(pow(enc,d,n)))
The vulnerability is quite obvious, mainly due to the gcd budget. If n and p run in a small range, just check whether there is k.
summary
Idol: if you can't do it in 10min, you can't do the foundation. It's really a sub question.
hh is very uncomfortable for me. For littlejunk, the foundation is really not strong, and the problem-solving experience is not good. It is always digging pits, and I don't know much about Android reverse. I still don't know some knowledge about line generation in rsa.
In short, if you love it, climb BA with me~