Catalog
Preface
stay [Algorithm 04] Tree and Binary Tree In this article, we will expand our explanation on the basis of binary trees, that is, binary search trees are built on the basis of trees.Why should bloggers spend an entire article on this binary search tree?The reason is simple. Red-black trees are based on binary search trees. If you don't know about binary search trees, what about red-black trees?Importance of Red-Black Tree I think you've never eaten Page meat and you've certainly seen Yichun Run.... Yes, the Map of jdk1.8 is a Hash list + red-black tree!
@
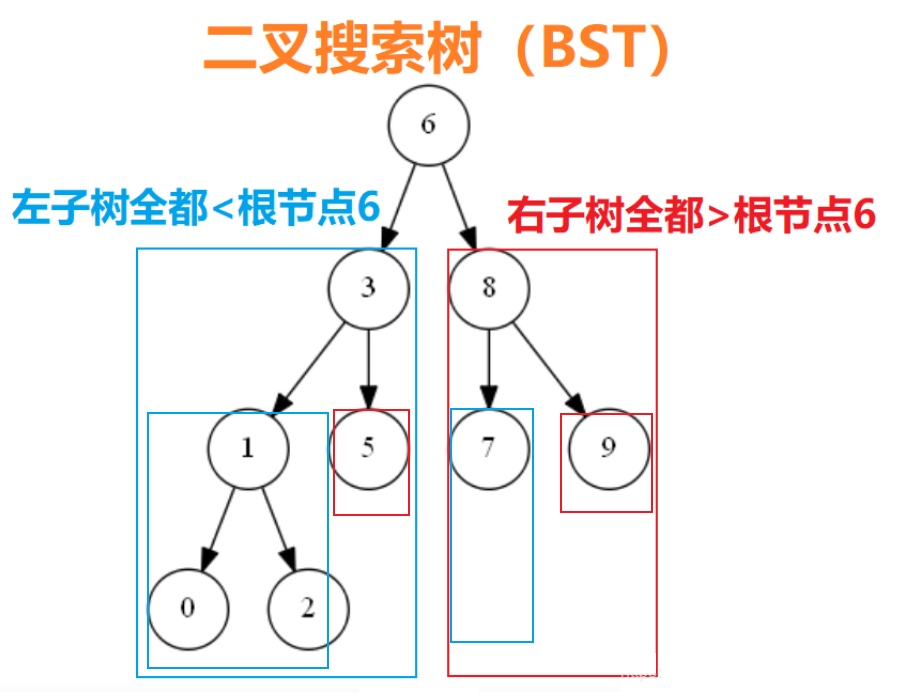
First of all, it should be clear that the binary search tree, also known as binary sort tree, binary search tree, or simply BST
1. Introduction to Dichotomy
Before formally launching the Binary Search Tree, Yichun would like to start by talking about life and life.
One day, programmer Lao Fang called Yichun: Beautiful boy, I ordered a pair of shoes today. Beautiful old man, the price is not bad!
Yichun: Come on, I don't know what it is. Let's return the leather shoes, the mouse leather shoes. If they are real cow leather shoes, I'll eat them!!!
Old Fang: Don't mention it, these shoes are really fake leather shoes which are better than real cow leather. Beautiful, guess how much silver I spent on them. Anyway, they are less than 100. See if you can guess it at least once again. If you guess it within five times, cook it in person, cook it for you, rattle it, hey...
Yichun: Do you suck or do you know me and know that I like this (self-blackness).... Cough and cough, 50 pieces
Lao Fang: No, the price is high
Yichun: 25
Lao Fang: No, the price is still high
Yichun: 12.5
....
A word by word, we estimate that each of you here is a talented person. In a simple game of dichotomy guessing numbers, we guess the final number by judging the guessing numbers "big" and "small".Of course, this can be described in two or three words. Yichun spent such a long string to describe it. It is estimated that Yichun TM is also a talented person.... In fact, Yichun would like to activate the atmosphere and concentrate your brain cells, which of course delayed your time. I'm sorry, Yichun was beaten online...
I don't know if you ever thought about it. Why is the dichotomy good enough?Can't I just guess 25 If it's less than 100?Is it not more likely to fix a price?In fact, guessing 25 or less directly is an extreme guess. If it is smaller than 25, then the range is less than 25. Have you ever thought: if it is greater than 25?The range goes directly to 75!As this extreme thought advances, you will find that
Each half-search will be more accurate and better able to handle all kinds of uncertain situations!The half-search complexity is O (log_2n), which means that it takes up to O (log_2n) times to guess the final number.
Now, to begin introducing the binary search tree officially, the binary search tree is actually similar to the binary search mentioned above, with a similar flavor.
2. Binary Search Tree Definition
Binary Search Tree (BST) is a special binary tree. A Binary Search Tree (BST) is a binary tree, where for each node in the tree:
1. If its left subtree exists, the value of each node in its left subtree is not greater than that of the node.
2. If its right subtree exists, the value of each node in its right subtree is not less than that of that node.
3. CRUD of Binary Search Tree
What I want to mention is that we know traversing trees in order of before, after and after, but traversing binary search trees is best done in order of middle. If you don't understand why you use middle order traversing, you have three options:
I. Self [Algorithm 04] Tree and Binary Tree Go in to complement the base tree
2. Leave a message to ask questions and return when Yichun sees them
3. Rejection from both Then you're excellent...
Then you're excellent...
3.1, Find
If you want to find any node in a binary search tree, assuming it is X, we can divide it into the following steps:
1. If the binary lookup tree is empty, the empty operation is returned, otherwise, perform an operation;
2. Take the root node first, and return if node X equals the root node;
3. If the node is smaller than the root node, the left subtree is found recursively.
4. If the node is larger than the root node, find the right subtree recursively.
//Lookup logical code implementation:
/**
* @param value The value you want to find the node
* @return Return null if found
*/
public Node search(int value) {
if(value == this.value) { //Find is this node
return this;
} else if(value < this.value) {//If the value found is less than the current node, recursively look to the left subtree
//If left subnode is empty
if(this.left == null) {
return null;
}
return this.left.search(value);
} else { //If the value found is not less than the current node, recursively look for the right subtree
if(this.right == null) {
return null;
}
return this.right.search(value);
}
}3.2, Insert
Insert a node in the binary tree, think carefully, you will find that inserting a node is usually inserted on the leaf node, so you only need to start from the root node, traverse through the data to be inserted and the size of the node in turn.
An important feature of a binary lookup tree is that it is almost as difficult to insert as to find.Inserting a node can actually be done in three ways:
1. If the tree is empty, insert the new node directly, otherwise, follow the steps below.
2. If the data to be inserted is larger than the root node data, insert new data into the right subtree. If the right subtree is empty, insert new data directly into the position of the right subtree. If not empty, continue traversing the right subtree to find the insertion location.
3. If the data to be inserted is smaller than the root node data, insert the data into the left subtree. If the left subtree is empty, insert the new data directly into the position of the left subtree. If not empty, continue traversing the left subtree to find the inserted location.
//Add Node Logic Code
//Add nodes in a recursive form, noting that you need to satisfy the requirements of a binary sort tree
public void add(Node node) {
if(node == null) {
return;
}
if(root == null) {
root = node;//If the root is empty, direct the root to the node
}
//Determine the value of the incoming node and its relationship to the root node of the current subtree
if(node.value < this.value) {
//If the left subnode of the current node is null
if(this.left == null) {
this.left = node;
} else {
//Recursively add to left subtree
this.left.add(node);
}
} else { //The value of the added node is greater than the value of the current node
if(this.right == null) {
this.right = node;
} else {
//Recursively add to right subtree
this.right.add(node);
}
}
}3.3, Delete
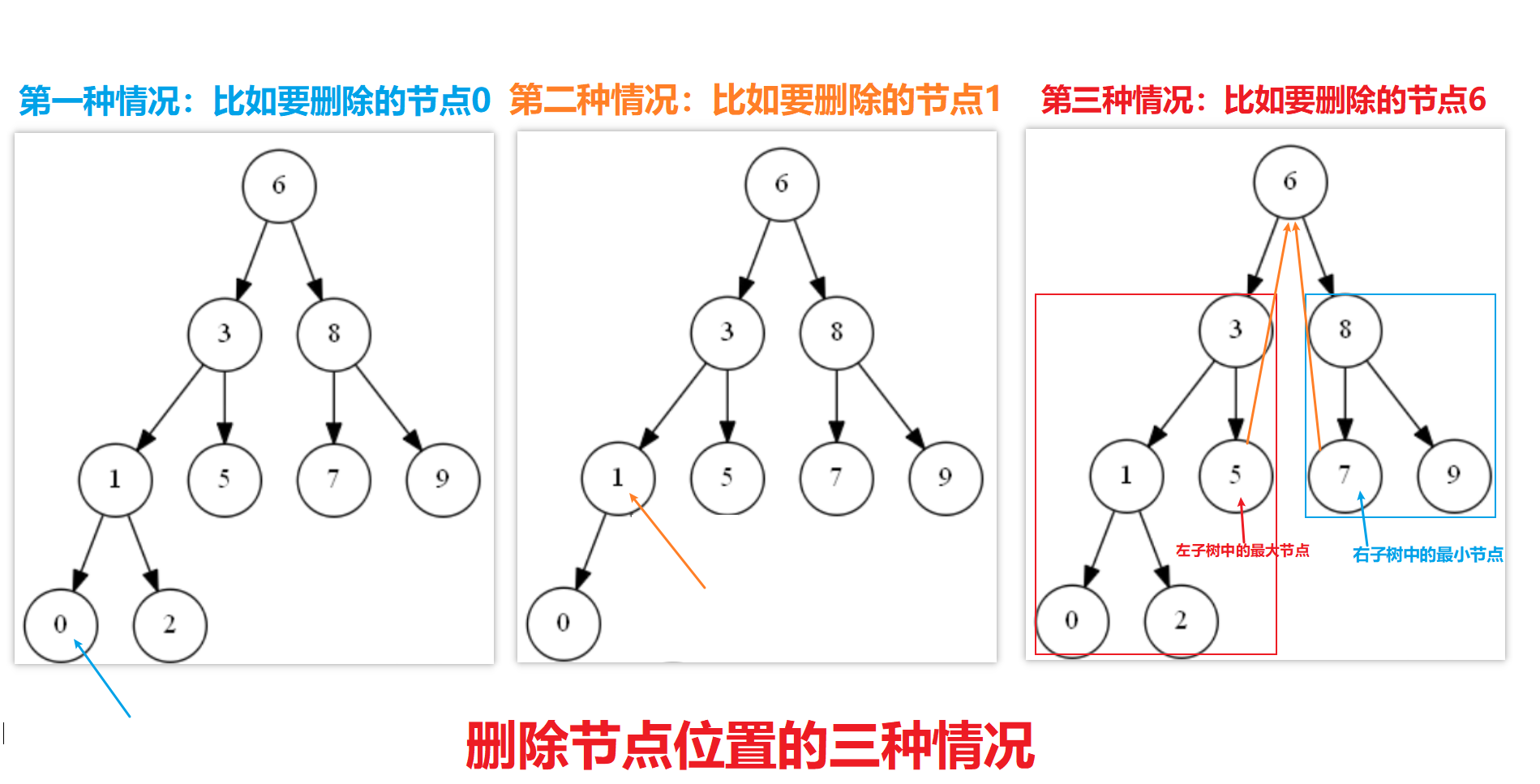
It can be said that deleting is more complex than finding and inserting. Why?Because to delete a node, first find the node and delete it, then restore the binary search tree to a binary search tree.Therefore, there are three general cases to deal with the different locations of the child nodes of the node to be deleted:
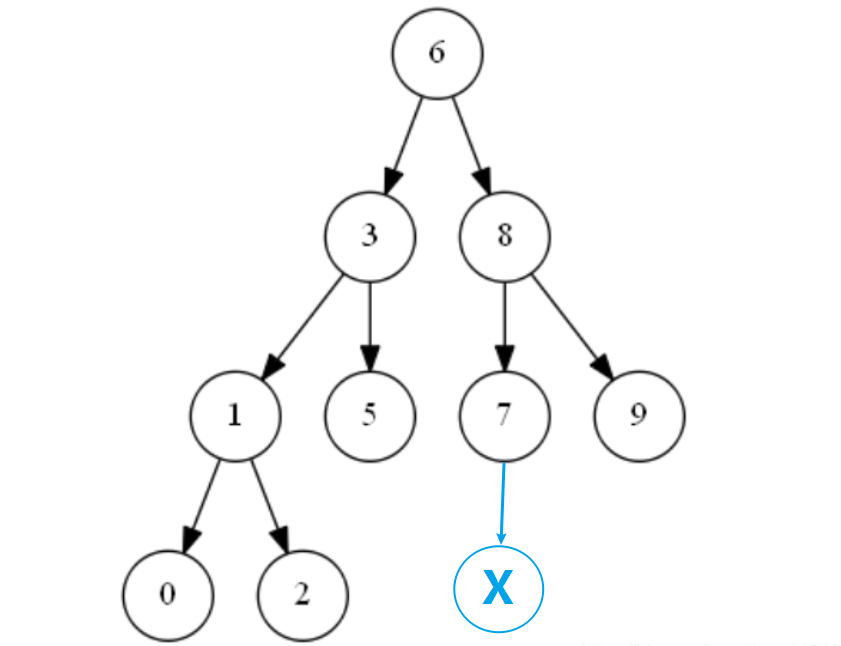
1. In the first case, if the node to be deleted has no children, point the pointer of the parent node to the node to be deleted directly to null.For example, node 0 to be deleted on the way.
2. In the second case, if the node to be deleted has only one node, that is, only the left or right child node, then the pointer to the parent node to be deleted points to the child node to be deleted.For example, Node 1 to be deleted on the way.
3. In the third case, if the node to be deleted has two children, the smallest node in the right subtree or the largest node in the left subtree of the node needs to be found first and replaced with the node to be deleted.Then delete the smallest node in the right subtree or the largest node in the left subtree, such as node 6 in the diagram to be deleted.
//Delete node logic code
public void delNode(int value) {
if(root == null) {
return;
}else {
//1. Need to find the node targetNode to delete first
Node targetNode = search(value);
//If no node was found to delete
if(targetNode == null) {
return;
}
//If we find that the current binary sort tree has only one node
if(root.left == null && root.right == null) {
root = null;
return;
}
//To find the parent node of targetNode
Node parent = searchParent(value);
//If the node to be deleted is a leaf node
if(targetNode.left == null && targetNode.right == null) {
//Determine whether targetNode is the left or right child of a parent node
if(parent.left != null && parent.left.value == value) { //Is Left Child Node
parent.left = null;
} else if (parent.right != null && parent.right.value == value) {//Is a child node
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) { //Delete nodes with two subtrees
int minVal = delRightTreeMin(targetNode.right);
targetNode.value = minVal;
} else { // Delete nodes with only one subtree
//If the node to be deleted has a left child node
if(targetNode.left != null) {
if(parent != null) {
//If targetNode is the left child node of parent
if(parent.left.value == value) {
parent.left = targetNode.left;
} else { // targetNode is the right child node of parent
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else { //If the node to be deleted has a right child node
if(parent != null) {
//If targetNode is the left child node of parent
if(parent.left.value == value) {
parent.left = targetNode.right;
} else { //If targetNode is the right child node of parent
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}3.4, Overall Code
To keep thinking consistently, you can edit the main method yourself for testing!
package dataStructure;
//Create Binary Sort Tree
class BinarySortTree {
private Node root;
public Node getRoot() {
return root;
}
//Find Nodes to Delete
public Node search(int value) {
if(root == null) {
return null;
} else {
return root.search(value);
}
}
//Find Parent Node
public Node searchParent(int value) {
if(root == null) {
return null;
} else {
return root.searchParent(value);
}
}
//Writing method:
//1. Value returned for the smallest node of a binary sorted tree with node as its root
//2. Delete the smallest node of a binary sorted tree whose node is the root node
/**
*
* @param node Incoming node (as root of binary sorted tree)
* @return Returns the value of the smallest node of a binary sorted tree with node as its root
*/
public int delRightTreeMin(Node node) {
Node target = node;
//Loop through the left child node to find the minimum
while(target.left != null) {
target = target.left;
}
//The target then points to the smallest node
//Delete Minimum Node
delNode(target.value);
return target.value;
}
//Delete Vertex
public void delNode(int value) {
if(root == null) {
return;
}else {
//1. Need to find the node targetNode to delete first
Node targetNode = search(value);
//If no node was found to delete
if(targetNode == null) {
return;
}
//If we find that the current binary sort tree has only one node
if(root.left == null && root.right == null) {
root = null;
return;
}
//To find the parent node of targetNode
Node parent = searchParent(value);
//If the node to be deleted is a leaf node
if(targetNode.left == null && targetNode.right == null) {
//Determine whether targetNode is the left or right child of a parent node
if(parent.left != null && parent.left.value == value) { //Is Left Child Node
parent.left = null;
} else if (parent.right != null && parent.right.value == value) {//Is a child node
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) { //Delete nodes with two subtrees
int minVal = delRightTreeMin(targetNode.right);
targetNode.value = minVal;
} else { // Delete nodes with only one subtree
//If the node to be deleted has a left child node
if(targetNode.left != null) {
if(parent != null) {
//If targetNode is the left child node of parent
if(parent.left.value == value) {
parent.left = targetNode.left;
} else { // targetNode is the right child node of parent
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else { //If the node to be deleted has a right child node
if(parent != null) {
//If targetNode is the left child node of parent
if(parent.left.value == value) {
parent.left = targetNode.right;
} else { //If targetNode is the right child node of parent
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
//Method of adding nodes
public void add(Node node) {
if(root == null) {
root = node;//If the root is empty, direct the root to the node
} else {
root.add(node);
}
}
//Intermediate traversal
public void infixOrder() {
if(root != null) {
root.infixOrder();
} else {
System.out.println("Binary sort tree is empty and cannot be traversed");
}
}
}
//Create Node Node
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
//Find Nodes to Delete
/**
*
* @param value Value of the node you want to delete
* @return Return null if found
*/
public Node search(int value) {
if(value == this.value) { //Find is this node
return this;
} else if(value < this.value) {//If the value found is less than the current node, recursively look to the left subtree
//If left subnode is empty
if(this.left == null) {
return null;
}
return this.left.search(value);
} else { //If the value found is not less than the current node, recursively look for the right subtree
if(this.right == null) {
return null;
}
return this.right.search(value);
}
}
//Find parent node to delete node
/**
*
* @param value Value of the node to be found
* @return Returns the parent of the node to be deleted, or null if not
*/
public Node searchParent(int value) {
//Return if the current node is the parent of the node to be deleted
if((this.left != null && this.left.value == value) ||
(this.right != null && this.right.value == value)) {
return this;
} else {
//If the value found is less than the value of the current node and the left child node of the current node is not empty
if(value < this.value && this.left != null) {
return this.left.searchParent(value); //Recursive search to left subtree
} else if (value >= this.value && this.right != null) {
return this.right.searchParent(value); //Recursive search to right subtree
} else {
return null; // No parent node found
}
}
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
//Method of adding nodes
//Add nodes in a recursive form, noting that you need to satisfy the requirements of a binary sort tree
public void add(Node node) {
if(node == null) {
return;
}
//Determine the value of the incoming node and its relationship to the root node of the current subtree
if(node.value < this.value) {
//If the left subnode of the current node is null
if(this.left == null) {
this.left = node;
} else {
//Recursively add to left subtree
this.left.add(node);
}
} else { //The value of the added node is greater than the value of the current node
if(this.right == null) {
this.right = node;
} else {
//Recursively add to right subtree
this.right.add(node);
}
}
}
//Intermediate traversal
public void infixOrder() {
if(this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if(this.right != null) {
this.right.infixOrder();
}
}
}
public class BinarySortTreeDemo { //============As for the main method, the test code can adjust itself!!!!!!!!
public static void main(String[] args) {
int[] arr = {4,7, 2, 13, 11, 5, 1, 9, 3};
BinarySortTree binarySortTree = new BinarySortTree();
for(int i = 0; i< arr.length; i++) {
binarySortTree.add(new Node(arr[i]));
}
binarySortTree.add(new Node(4));
System.out.println("Medium Order Traversal Binary Sort Tree~");
binarySortTree.infixOrder();
}
}4. Two extreme cases of binary search trees
1. Turn into a complete binary tree, where all nodes try to fill each layer of the tree. If there are remaining nodes after the previous layer is filled, fill the next layer as far as possible from left to right.As shown in the following figure, it is a complete binary tree.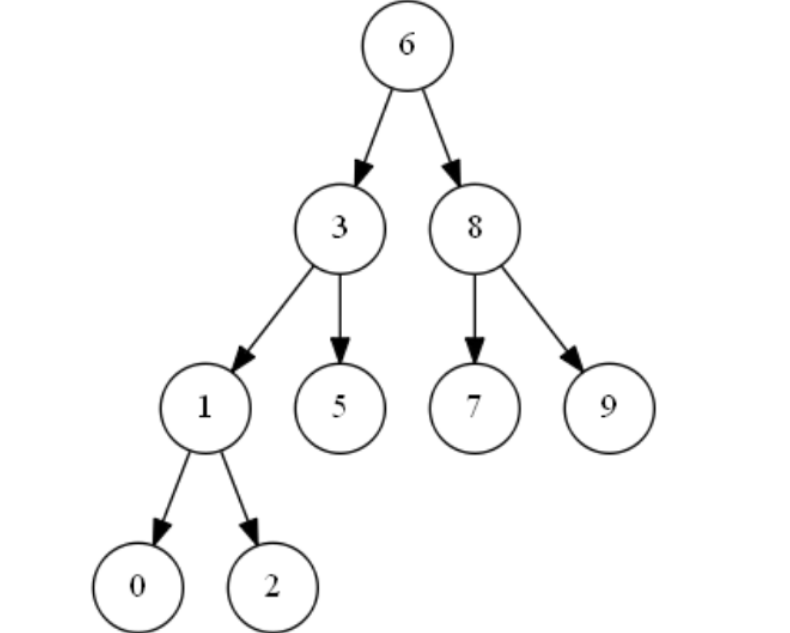
2. A binary tree with only one node per layer.As shown in the following figure: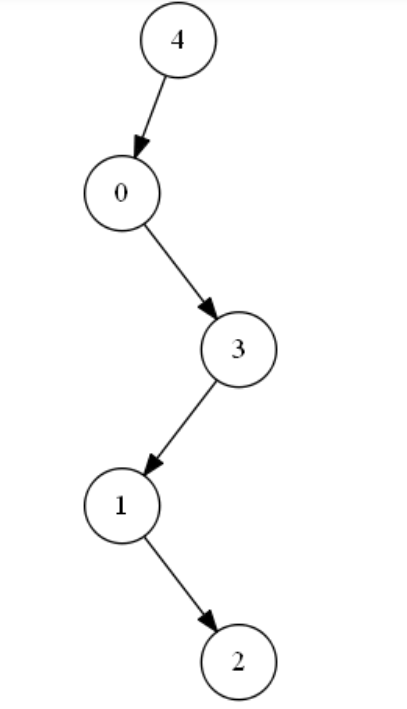
I hit, isn't this a Snake Peel Monster Single Chain List? Yes, it gives us the feeling that the Tree Monster has degenerated into a Snake Peel Monster Single Chain List!In this case, there is only one node per layer in the tree, and the tree structure in this state tends to be a linear structure. The query of nodes is similar to traversal of arrays with O(n) complexity.
It is for this reason that there is a balanced binary tree, which involves the snakeskin operation of the whistle in the left-handed right-handed flower. Of course, this is just mentioned, not in the scope of this article, but the following articles should be written in this regard, try to.....
5. Summary of Binary Search Tree
Binary Search Tree is also called Binary Sort Tree, Binary Find Tree, or BST
Based on the characteristics of the binary search tree, ==Knowable number of comparisons equals the number of layers of a given value node in the binary sort tree==.Traverse in middle order.If the binary sorting tree is balanced, the height of the binary sorting tree with n nodes is Log2n+1, and its search efficiency is O(Log2n), which is similar to a half-fold search.If the binary sorting tree is completely unbalanced, its depth can reach n, its search efficiency is O(n), and it degenerates to sequential search.Generally, the search performance of binary sorted trees is between O(Log2n) and O (n).Therefore, in order to obtain better search performance, a balanced binary sorting tree needs to be constructed.The balanced binary tree may also involve the whistling snakeskin operation in the left-handed right-handed flowers. Of course, this is just mentioned, not in this article, but you should write about it later, try your best...
If this article helps you a little, please give a compliment, thank you~
Finally, if there are any deficiencies or inaccuracies, you are welcome to correct the criticism and appreciate it!If in doubt, please leave a message and reply immediately!
Welcome to my Public Number, which contains some java learning materials and a large wave of Java e-books, such as Professor Zhou Zhiming's in-depth Java virtual machine, Java programming ideas, core technology volume, big story design mode, Java Concurrent Programming practice.....are all the Bibles of java, let's not say get on the Tomcat car, let's go!The most important thing is to explore technology together, yearn for technology, and pursue technology. Well, if you come, you'll be friends.
