catalogue
1. The deleted node D is a leaf node
2. The deleted node D has only one child
2-1. Delete node 14 (left or right)
2-2. Delete node {10 (right or left)
3. Both left and right children of the deleted node exist
Method 1: replace the root node with the largest node of the left subtree
Method 2: replace the root node with the smallest node of the right subtree
1, Basic theory
1. Features:
(1) If its left subtree is not empty, the values of all nodes on the left subtree are less than the values of its root node;
(2) If its right subtree is not empty, the values of all nodes on the right subtree are greater than the values of its root node;
(3) Its {left and right subtrees are binary sort trees respectively.
2. Structure:
Binary tree
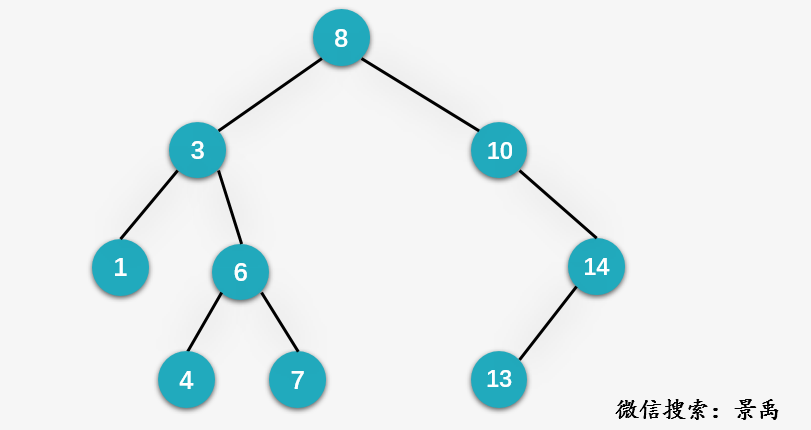
2, Search
(1) Starting from the root, if not found, obtain the empty node address and return;
(2) If equal, find, prompt and exit;
(3) Key < node, traversing left (recursive lchild)
(4) Key > node, right traversal (recursive rchild)
(you can locate while searching, and finally return to the location to be searched)
The search operation of binary sort tree is very similar to binary search. Let's try to find the node with the value of 13.
Step 1: access the root node {8
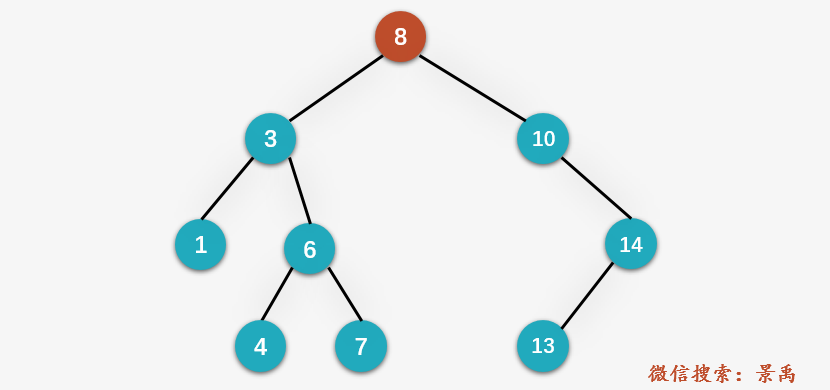
Step 2: according to the property that the left subtree of the binary sort tree is smaller than the root node and the right subtree is larger than the root node, 13 > 8, so the node with the value of 13 may be in the right subtree of root node 8. Let's check the right subtree of root node # 10:

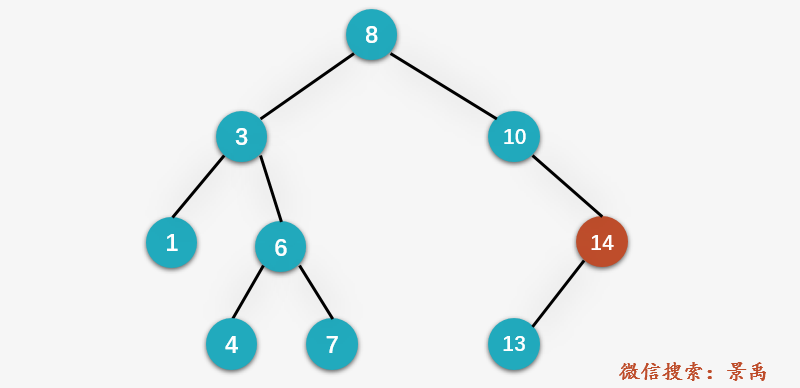
Step 3: similar to step 2, 13 > 10, so check the right child of node ^ 10 ^ 14:
Step 4: according to the property that the left subtree of the binary sort tree is smaller than the root node and the right subtree is larger than the root node, 13 < 14. Therefore, check the left subtree of ^ 13, and find that it is just equal to the value to be found:
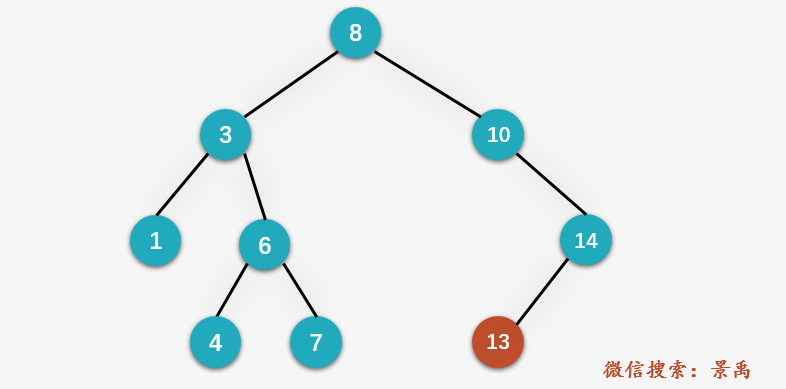
//Find binary sort tree
void Search_BST(pBiTree* T, int key) //keyword
{
//Search failed (no value, need to add)
if (!(*T))
{
p = T;
return;
}
//Search succeeded
if (key == (*T)->data)
{
printf("Search succeeded!\n");
success = 1;
return;
}
else if (key < (*T)->data)
Search_BST(&((*T)->lchild), key); //Small, traverse to the left
else
Search_BST(&((*T)->rchild), key); //Large, traverse to the right
}3, Insert
Find it first, locate it to the position to be inserted, and insert it directly.
The first node is placed in the root, and the following nodes are judged with each node in front. The small node is placed on the left and the large node is placed on the right.

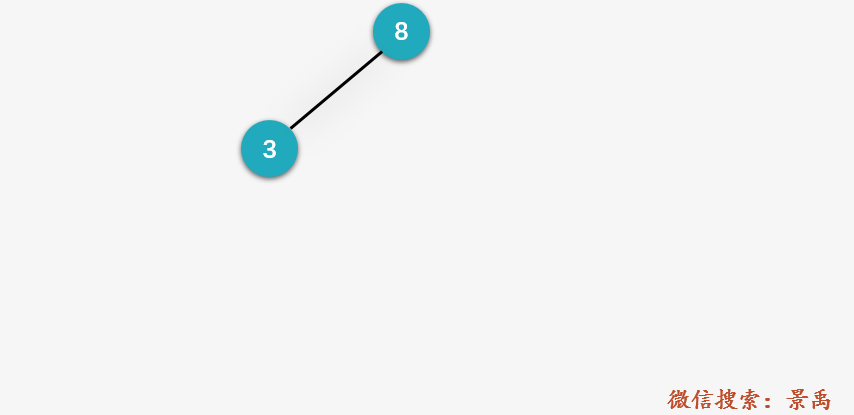

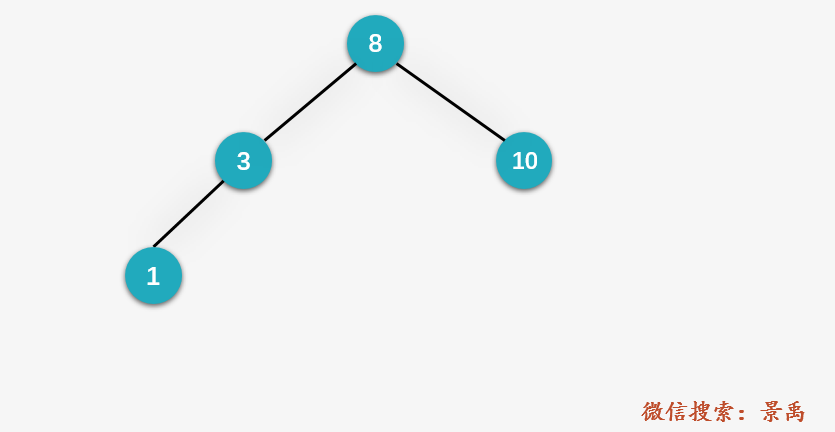

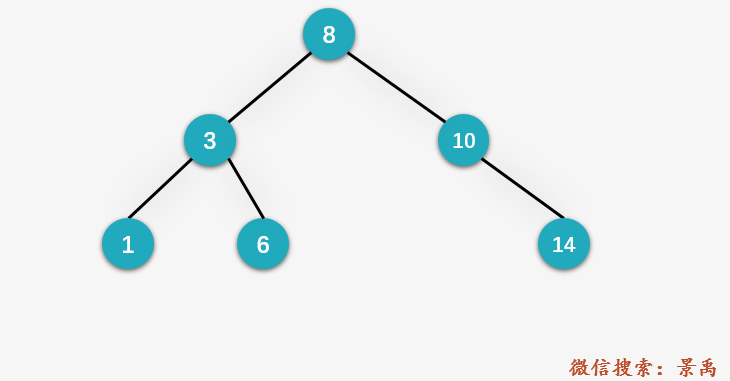
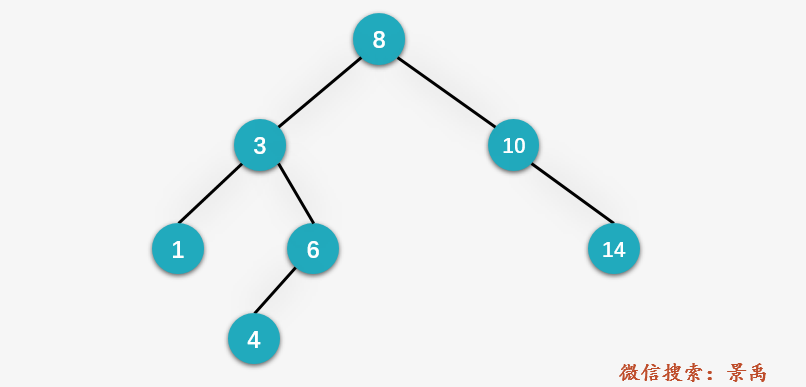
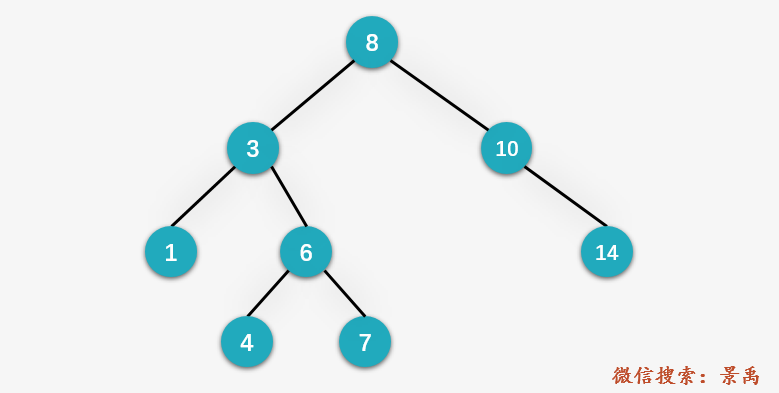
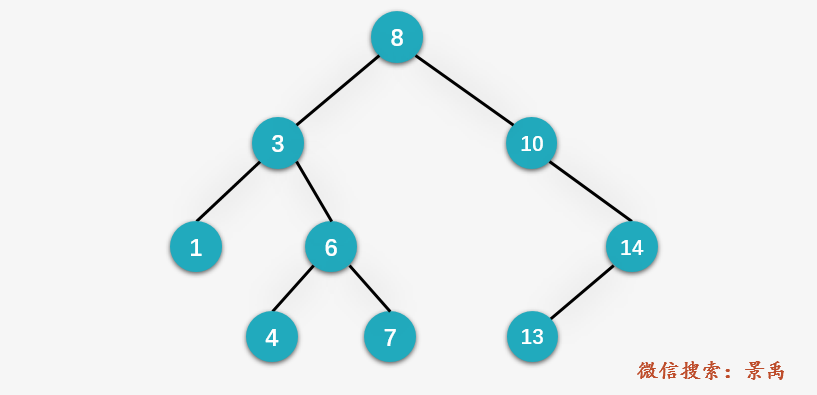

Code
//Insert binary sort tree
void Insert_BST(int key) //Indexes
{
Search_BST(&head, key);
//find
if (success)
return;
//Not found (create a new node to accommodate)
(*p) = (pBiTree)malloc(sizeof(pBiTree));
(*p)->data = key; //storage
//Assign null values to the left and right subtrees
(*p)->lchild = NULL;
(*p)->rchild = NULL;
}4, Delete
The delete operation is different from the find and insert operations. We need to deal with it in the following three cases:
1. The deleted node D is a leaf node
You can delete it directly from the binary sort tree, and it will not affect the structure of the tree.

2. The deleted node D has only one child
(1) If there are only left children and no right children, you only need to link the left child of the node to be deleted to the parent node of the node to be deleted, and then delete node D; (overwrite)
(2) If there is only a right child and no left child, just reconnect the right child to delete node d to the parent node to delete node D. (overwrite)
2-1. Delete node 14 (left or right)
Overlay.
Save node # 13 # where node # 14 # is to be deleted to the temporary variable temp, and delete node # 14;

Set {right child} of the parent node} 10} of the deleted node {14} to temp, that is, node} 13.
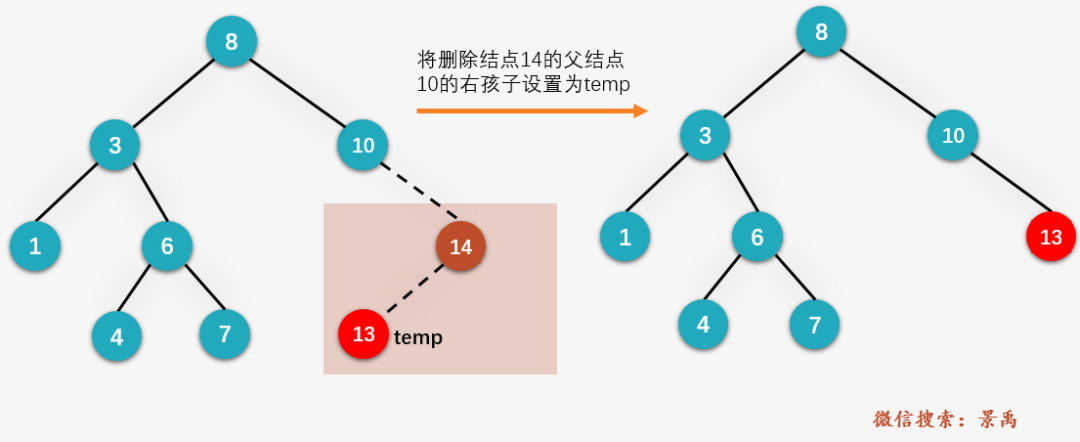
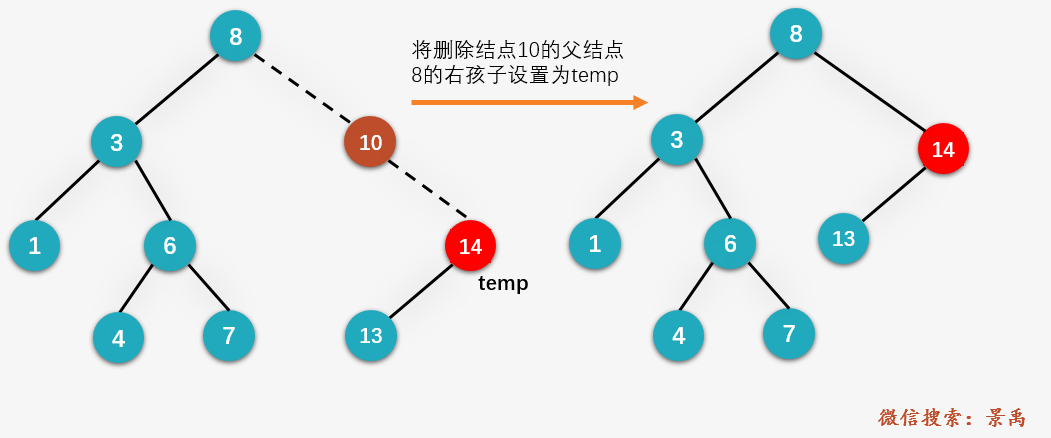
2-2. Delete node {10 (right or left)
Overlay.
Save node # 14 # of node # 10 # to be deleted to the temporary variable temp, and delete node # 10;

Set {right child} of the parent node {8} of the deleted node {10} to temp, that is, node} 14.
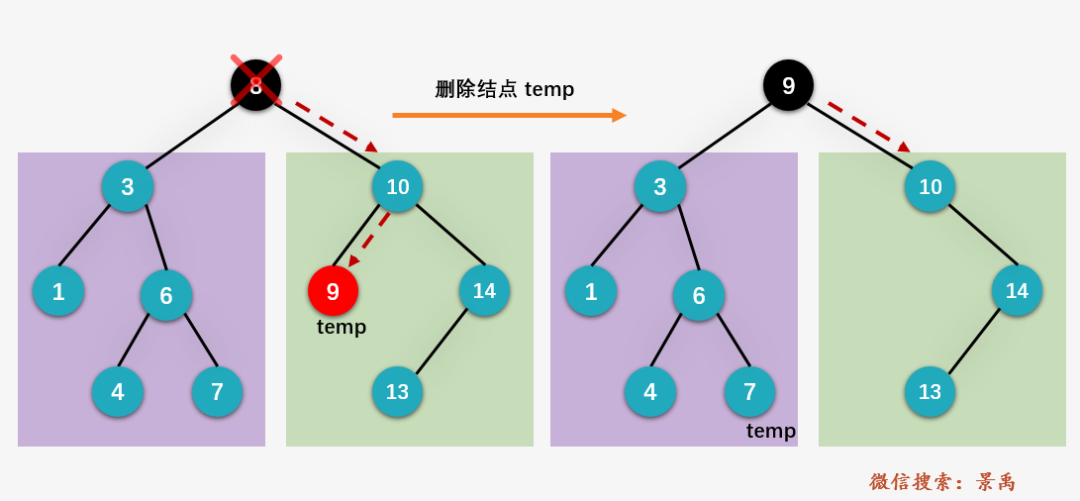
3. Both left and right children of the deleted node exist
Replace the vertex with the maximum value in the left subtree or the minimum value in the right subtree.
(this situation is more complicated. This time, we will make the graph a little more complicated and add a left child node to the original node # 10 # 9.)
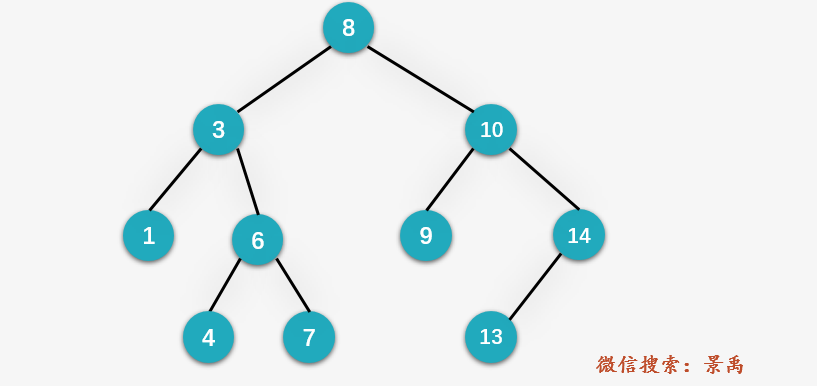
The middle order traversal results of the above binary sort tree are as follows:

Take deleting vertex 8 as an example:


Method 1: replace the root node with the largest node of the left subtree
(1) Get the largest node in the left subtree 7

(2) Replace the value of deleted node {8} with {7}
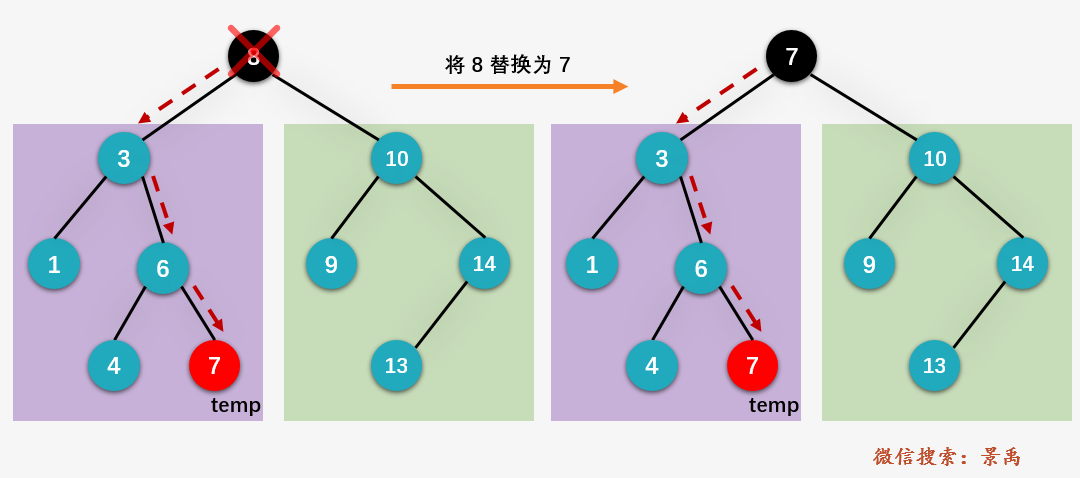
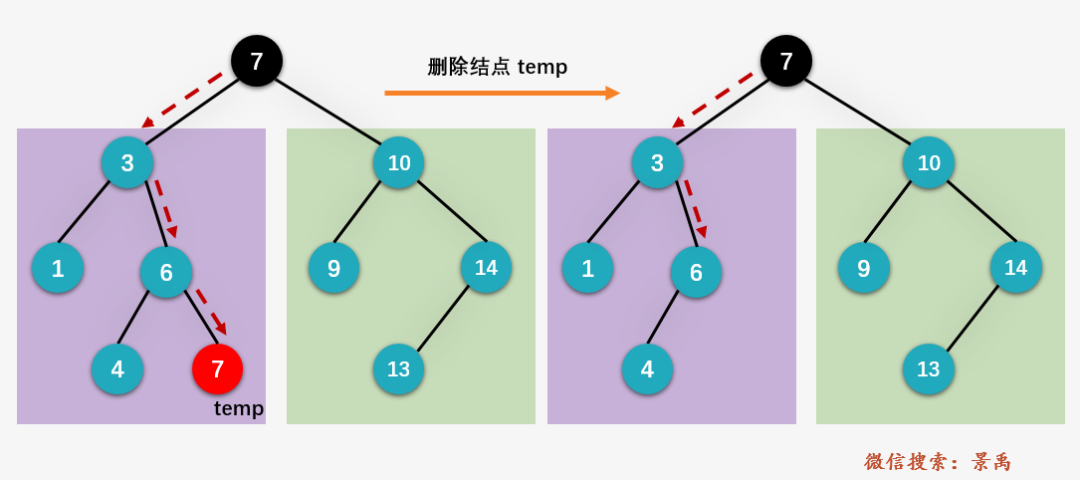
(3) Delete the left subtree of the root node as the node with the largest median (consider whether the node has left children)
Method 2: replace the root node with the smallest node of the right subtree
(1) Find and delete the right subtree of node ^ 8 ^ and the node with the smallest median, that is, ^ 9

(2) Replace the value of deleted node , 8 , with , 9
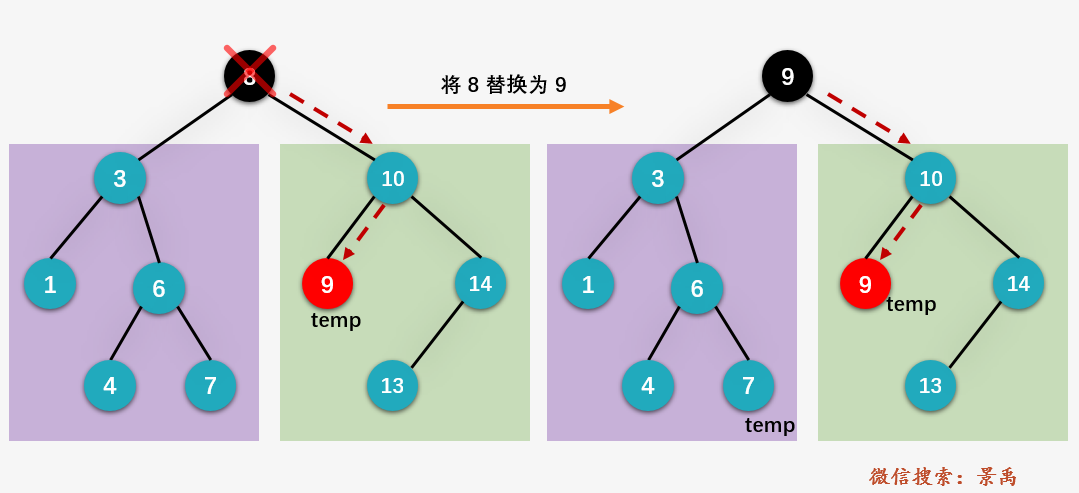
(3) Delete the right subtree of the root node as the node with the smallest median (consider whether the node has right children)
Code 1: locate the node to be deleted
//Delete (locate the deleted node)
void Delete_BST(pBiTree* p, int key)
{
if (*p) //Node exists
{
if (key == (*p)->data)
Delete(p);
else if (key < (*p)->data)
Delete_BST(&(*p)->lchild, key); //Recursive left
else
Delete_BST(&(*p)->rchild, key); //Recursive right
}
}Code 2: single node deletion
//Delete Vertex
void Delete(pBiTree* p)
{
pBiTree s;
//1. Left and right are empty
if (!(*p)->lchild && !(*p)->rchild)
*p = NULL;
//2. Left subtree is empty
else if (!(*p)->lchild)
*p = (*p)->rchild; //cover
//3. The right subtree is empty
else if (!(*p)->rchild)
*p = (*p)->lchild; //cover
//4. The left and right subtrees are not empty (two methods: find the maximum value of the left subtree / find the minimum value of the right subtree)
//Here, choose to find the maximum value of the left subtree
else
{
pBiTree q = (*p);
s = (*p)->lchild; //Locate the left subtree first
while (s->rchild)
{
q = s; //Save previous node
s = s->rchild; //Look back
}
(*p)->data = s->data; //cover
//Consider: there is a left node
p = &q; //Navigate to previous node
(*p)->rchild = s->lchild; //Reconnecting q right subtree
}
}Total code
//Binary sort tree (find, insert, delete)
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
#define MAXSIZE 20
int data[MAXSIZE];
int length = 0; //Array length
int success = 0; //Is the record found successfully
//Binary tree structure
typedef struct BiTree
{
int data;
struct BiTree* lchild, * rchild;
}BiTree, * pBiTree, ** p2BiTree;
BiTree* head;
pBiTree* p;
//input data
void Input()
{
int Data;
int i = 0;
printf("Please enter initial data:\t");
//input data
do
{
scanf("%d", &Data);
data[i++] = Data;
} while (getchar() != '\n');
length = i; //Record array length
}
//Binary tree initialization
void Init_BiTree()
{
head = NULL;
}
//Find binary sort tree
void Search_BST(pBiTree* T, int key) //keyword
{
success = 0; //Initialization does not affect the search results
//Search failed (no value, need to add)
if (!(*T))
{
p = T;
return;
}
//Search succeeded
if (key == (*T)->data)
{
printf("Search succeeded!\n");
success = 1;
return;
}
else if (key < (*T)->data)
Search_BST(&((*T)->lchild), key); //Small, traverse to the left
else
Search_BST(&((*T)->rchild), key); //Large, traverse to the right
}
//insert
void Insert_BST(int key) //Indexes
{
Search_BST(&head, key);
//find
if (success)
return;
//Not found (create a new node to accommodate)
(*p) = (pBiTree)malloc(sizeof(pBiTree));
(*p)->data = key; //storage
//Assign null values to the left and right subtrees
(*p)->lchild = NULL;
(*p)->rchild = NULL;
}
//Delete Vertex
void Delete(pBiTree* p)
{
pBiTree s;
//1. Left and right are empty
if (!(*p)->lchild && !(*p)->rchild)
*p = NULL;
//2. Left subtree is empty
else if (!(*p)->lchild)
*p = (*p)->rchild; //cover
//3. The right subtree is empty
else if (!(*p)->rchild)
*p = (*p)->lchild; //cover
//4. The left and right subtrees are not empty (two methods: find the maximum value of the left subtree / find the minimum value of the right subtree)
//Here, choose to find the maximum value of the left subtree
else
{
pBiTree q = (*p);
s = (*p)->lchild; //Locate the left subtree first
while (s->rchild)
{
q = s; //Save previous node
s = s->rchild; //Look back
}
(*p)->data = s->data; //cover
//Consider: there is a left node
p = &q; //Navigate to previous node
(*p)->rchild = s->lchild; //Reconnecting q right subtree
}
}
//Delete (locate the deleted node)
void Delete_BST(pBiTree* p, int key)
{
if (*p) //Node exists
{
if (key == (*p)->data)
Delete(p);
else if (key < (*p)->data)
Delete_BST(&(*p)->lchild, key); //Recursive left
else
Delete_BST(&(*p)->rchild, key); //Recursive right
}
}
//Middle order traversal output
void Inorder_Traverse(pBiTree p)
{
if (p)
{
Inorder_Traverse(p->lchild);
printf("%d ", p->data);
Inorder_Traverse(p->rchild);
}
}
int main()
{
int key;
Input(); //input
Init_BiTree(); //Binary tree initialization
for (int i = 0; i < length; i++)
Insert_BST(data[i]); //Insert binary sort tree
//delete
printf("\n Please enter the data to be deleted:\t");
scanf("%d", &key);
Delete_BST(&head, key);
//lookup
printf("Please enter the data to query:\t");
scanf("%d", &key);
Search_BST(&head, key);
//insert
printf("\n Please enter the data to be inserted:\t");
scanf("%d", &key);
Insert_BST(key);
//lookup
Search_BST(&head, key);
Inorder_Traverse(head); //Traversal (medium order traversal, output from small to large)
return 0;
}