catalogue
Detecting rings in directed graphs
Vertex sorting based on depth first
Directed graph
Definition of directed graph and related terms
Definition:
A directed graph is a directional graph, which is composed of a group of vertices and a group of directional edges, and the edges in each direction are connected
A pair of ordered vertices.
Output:
The number of edges indicated by a vertex is called the extroversion of the vertex.
Penetration:
The number of edges pointing to a vertex is called the penetration of the vertex.
Directed path:
It consists of a series of vertices. For each vertex, there is a directed edge from which to point to the next vertex in the sequence.
Directed ring:
- a directed path with at least one edge and the same starting and ending points.
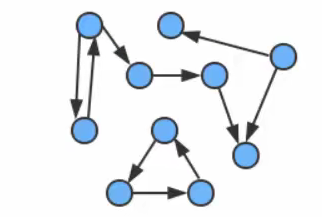
The two vertices v and w in a directed graph may have the following four relationships:
1. No edge connection;
2. There is an edge from v to w, v - > w;
3. There is an edge W from w to v - > v;
4. There are both sides from w to v and sides from v to W, that is, two-way connection;
Understanding a directed graph is relatively simple, but it is not so easy to see the path in a complex directed graph through the eyes.
Directed graph API design

A reverse graph is designed in the api, because in the implementation of directed graph, the other vertices pointed by the current vertex v are obtained by adj method. If we can get its reverse graph, we can easily get other vertices pointing to v.
Realization of directed graph
// Directed graph
public class Digraph {
// Record the number of vertices
private final int V;
//Number of recording edges
private int E;
//Define adjacency table of directed graph
private Queue <Integer>[] adj;
public Digraph (int v) {
//Number of initialization vertices
this.V = v;
//Number of initialized edges
this.E = 0;
//Initialize adjacency table
adj = new LinkedList[v];
//Initialize empty queue of adjacency table
for (int i = 0; i < v; i++) {
adj[i] = new LinkedList<>();
}
}
public int V () {
return V;
}
public int E () {
return E;
}
//Add a directed edge of V - > W
public void addEage (int v , int w) {
adj[v].add(w);
++E;
}
//Gets all vertices pointed to by vertex v
public Queue<Integer> adj (int v) {
return adj[v];
}
//Reverse the directed graph and return
public Digraph reverse () {
//Create a reverse graph
Digraph reverseDigraph = new Digraph(V);
//Get each node of the original directed graph
for (int i = 0; i < V; i++) {
//Get all nodes of each node adjacency table
for (Integer w : adj[i]) {
//Reverse the diagram and record W - > v
reverseDigraph.adj(w).add(i);
}
}
return reverseDigraph;
}
}
Topological sorting
In real life, we often receive many tasks at one time, but these tasks are completed in order. Taking the subject of java as an example, we need to learn a lot of knowledge, but these knowledge needs to be completed in order in the process of learning. It is a step-by-step and dependent process from java foundation to jsp/servlet, ssm and spring boot. Before learning jsp, you should first master the basics of java and html, and jsp/servlet before learning ssm framework.
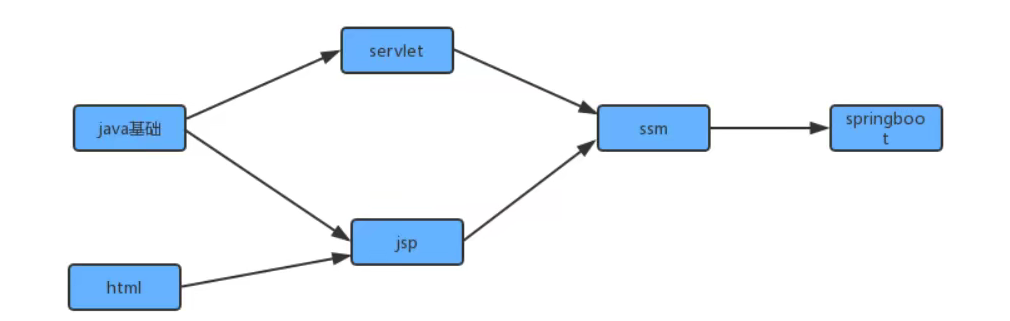
In order to simplify the problem, we use the standard model with integer as vertex number to represent this case:
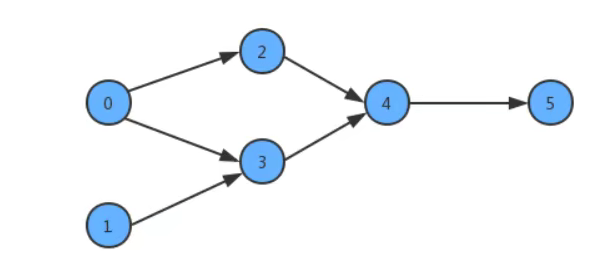
At this time, if a student wants to learn these courses, he needs to specify a learning scheme. We only need to sort the vertices in the graph and convert them into a linear sequence to solve the problem. At this time, we need to use an algorithm called topological sorting.
Topological sorting
Given a directed graph, all vertices are sorted so that all directed edges point from the front element to the back element. At this time, the priority of each vertex can be clearly expressed. The following is a schematic diagram after topological sorting: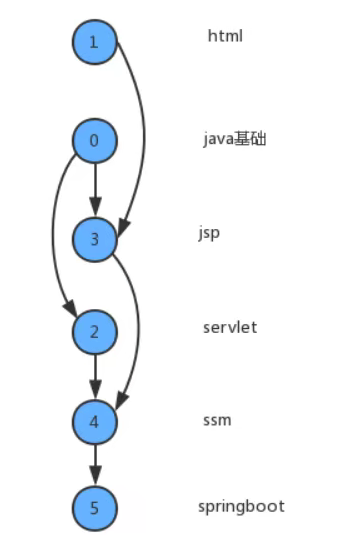
Detecting rings in directed graphs
If you have to learn course y before learning course x, course z before learning course y, and course x before learning course z, there must be a problem. We can't learn because these three conditions can't be met at the same time. In fact, the conditions of these three courses x, y and z form a ring:
Therefore, if we want to use topological sorting to solve the priority problem, we must first ensure that there are no rings in the graph.
API design for detecting directed ring
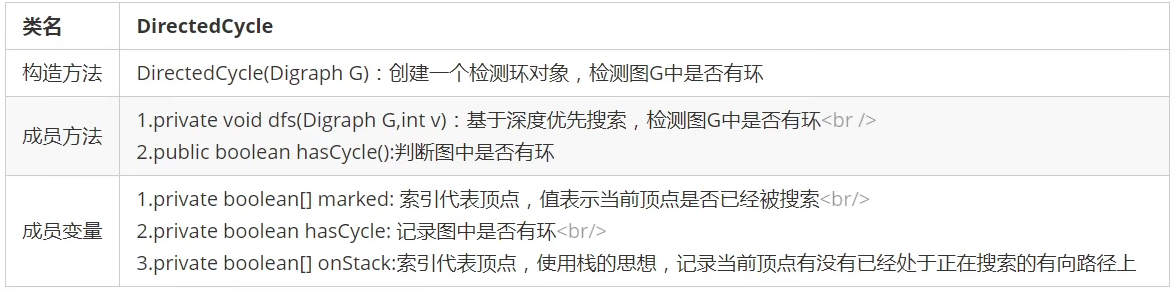
Implementation of detection directed loop
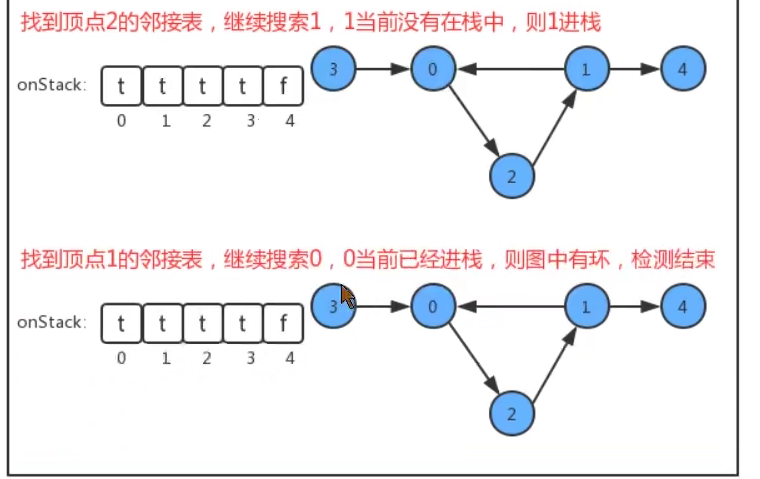
onStack [] Boolean array is added to the API. The index is the vertex of the graph. When we search deeply:
1. If the current vertex is being searched, change the value in the corresponding onStack array to true and mark it into the stack;
2. If the current vertex search is completed, change the value in the corresponding onStack array to false to identify the stack;
3. If you are about to search for a vertex, but the vertex is already in the stack, there is a ring in the graph;

Code
/**
* Check for rings in the illustration
*/
public class DirectedCycle {
/**
* The index represents the vertex, which is used to record whether the vertex has been searched
*/
private boolean[] marked;
/**
* Judge whether there is a ring in the diagram
*/
private boolean hasCycle;
/**
* The idea of stack is used to record whether the current vertex already exists on the current search path
* If it exists, it can be judged that there is a ring in the graph
*/
private boolean[] onStack;
/**
* Judge whether the incoming directed graph has a ring
* @param G
*/
public DirectedCycle (Digraph G) {
marked = new boolean[G.V()];
onStack = new boolean[G.V()];
hasCycle = false;
//Because I don't know that there may be a ring from that point
//Therefore, we need to search from all vertices to judge whether there is a ring
for (int i = 0; i < G.V(); i++) {
dfs(G,i);
}
}
/**
* Using depth search to judge whether there is a ring in a directed graph
* onStack Enter and exit the stack, and then judge whether the currently searched vertex is already on the search path
*
* @param G
* @param v
*/
private void dfs (Digraph G,int v) {
//Marked vertices have been searched
marked[v] = true;
for (Integer adj : G.adj(v)) {
//Determine whether v is already on the search path
if(marked[adj] && onStack[adj]) {
//Existential ring
hasCycle = true;
}else {
//Adopt the idea of backtracking
//Stack vertices
onStack[adj] = true;
dfs(G,adj);
//Backtracking vertex out of stack
onStack[adj] = false;
}
}
}
/**
* Determine whether there is a ring
* @return
*/
public boolean hasCycle(){
return hasCycle;
}
}
Vertex sorting based on depth first
If we want to generate a linear sequence of vertices in a graph, it is actually a very simple thing. We have learned and used depth first search for many times before. We will find that depth first search has a feature, that is, on a connected subgraph, each vertex will only be searched once. If we can add a line of code on the basis of depth first search, We can do this by simply putting the vertices of the search into the data structure of the linear sequence.
Vertex sorting API design

Implementation of vertex sorting
In the design of API, we add a stack reversePost to store vertices. When we search the graph in depth, after each vertex is searched, put the vertex into reversePost, so as to realize vertex sorting.

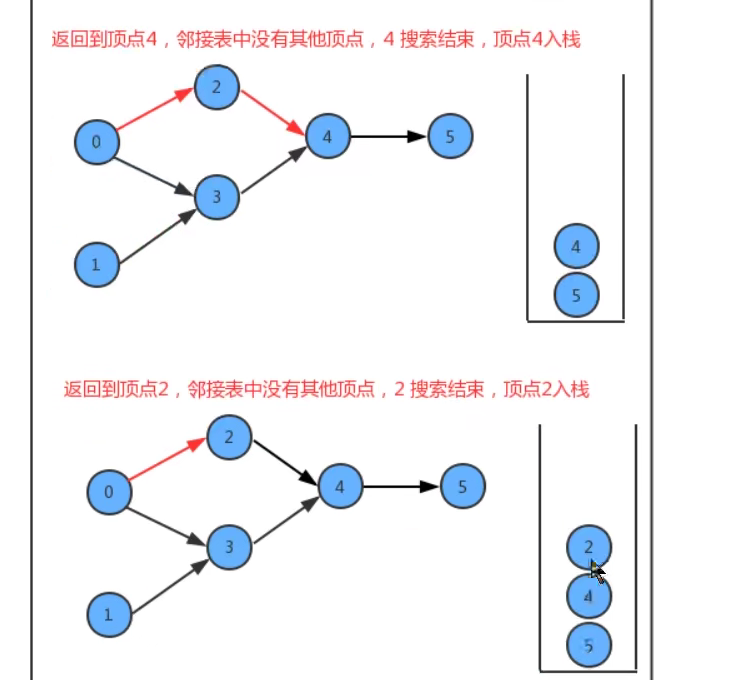
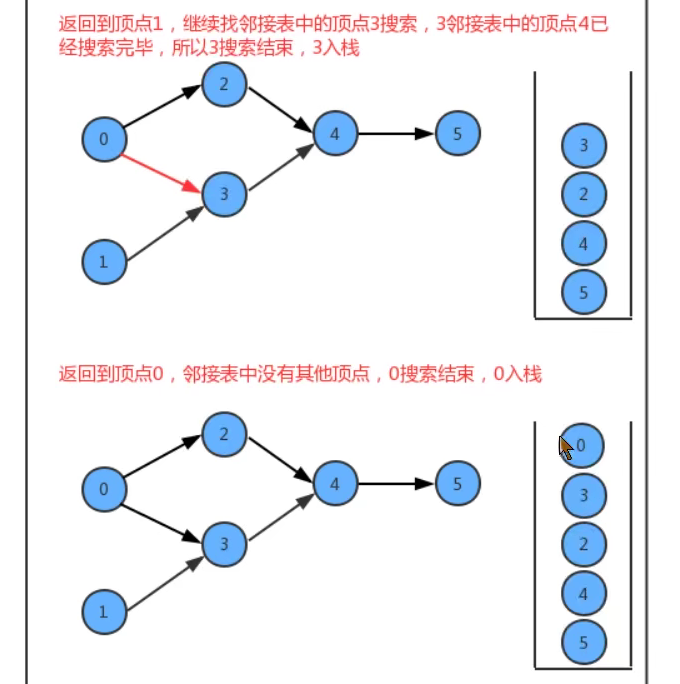
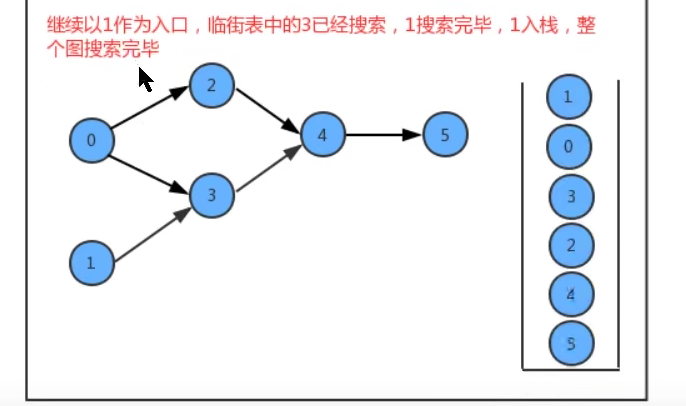
Code:
/**
* Vertex sorting for depth first search
*/
public class DepthFirstOrder {
/**
* The index represents the vertex, which is used to record whether the vertex has been searched
*/
private boolean[] marked;
/**
* Use stack records to search vertices under depth first
*/
private Stack<Integer> reversePost;
public DepthFirstOrder (Digraph G) {
marked = new boolean[G.V()];
reversePost = new Stack<>();
for (int i = 0; i < G.V(); i++) {
//If the vertex has been searched, it is not used
if(!marked[i])
dfs(G,i);
}
}
/**
* A linear sequence of vertices is generated based on depth first search
* @param G
* @param v
*/
private void dfs (Digraph G, int v) {
//Marked vertices have been searched
marked[v] = true;
for (Integer w : G.adj(v)) {
if(!marked[w])
dfs(G,w);
}
//Record in linear sequence
reversePost.push(v);
}
/**
* Get linear sequence of vertices
* @return
*/
private Stack<Integer> ReversePost() {
return reversePost;
}
}