subject

thinking

Find the next array

for instance

! [insert picture description here]( https://img-blog.csdnimg.cn/5c94e122d0384afaaa021e1ff505e7da.png

When our program is judging that the last a of 2 string does not match the substring of 1 string, we don't need to judge whether the middle a needs to be
Let's just move the whole follow-up part behind a, so the question is, how many a?
In this topic, it should be moving into this situation

Put the first a in the mismatched area
(if you don't understand, give another example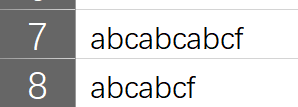
The mismatches here are a and f, so we should find the c in front of f in the 8 string to judge how many steps to move. If we move 6 steps directly, we will lose the matching situation when moving 3 steps

How to find the number of steps to move for each position of a short string?

At this time, we need to observe the string
Take the second example
When f there is a mismatch, we have to look at the previous abcabc section to see whether the "suffix" and "prefix" are the same

It is not difficult to find that when the length is 3, the prefix and suffix are the same. At this time, we need to move back 6-3 = 3 steps to ensure that the abc part can still match the abc in the previous part when you next match. At this time, compare them one by one from the fourth position a

(subsets with length 6 must be equal. At this time, it is meaningless to move 6-6 = 0 steps)

Therefore, we can easily get the next comparison content corresponding to each position of the substring
(Note: if I does not match, the next match is next[i-1], that is, the prefix corresponding to the number of i-1)

"When the first character does not match, we default to - 1 (it can also be 0, just one digit short)
a. The common prefix is itself. Move back 1 - 0 = 1 step, and the cursor moves to a as 0
ab, the public pre suffix is only 2 (itself), so we can think that there is no public pre suffix. The moving size is 2 - 0 = 2 steps. In the program, move the comparison cursor to a as 0
abc is the same as above, move 3 - 0 = 3, and move the cursor to 0 on a
The maximum suffix before abca is 1 (remove the one equal to itself), so move 4 - 1 = 3 steps and move the cursor to b 1
The maximum suffix before abcab is 2, so move 5 - 2 = 3 steps and move the cursor to c 2
The maximum suffix before abcabc is 3, move 6 - 3 = 3 steps, and move the cursor to c
So we get the following table
,
Get next array code

int getIn(string a, string b)
{
    int bl = b.length();
    //Get next array part
    int i = 0, j = -1;
    int* next = new int[b.length() + 10];
    memset(next, 0 ,sizeof(next));
    next[0] = -1;
    while(i < b.length())
    {
        if(j == -1 || b[i] == b[j])
        {
            i++;j++;
            next[i] = j;
        }
        else
        {
            j = next[j];//The subscript changes back to 0, which moves all the previous parts
        }
    }
}

Find KMP matching code

int firIn(string a, string b, int* next)
{
    int i = 0, j = 0;
    int al = a.length(), bl = b.length();
    while(i < al && j < bl)
    {
        if(j == -1 || a[i] == b[j])
        {
            i++;j++;
        }
        else
            j = next[j];
			//The right shift of short string is equal to the left shift of long string
    }

    if(j >= bl)
        return i - bl;
    else return -1;
}

code

#include<iostream>
#include<string.h>
using namespace std;

void print(int* next, int l)
{
    for(int i = 0; i < l; i++)
        cout << next[i] << " ";
    cout << endl;
}
int firIn(string a, string b, int* next)
{
    
}

int getIn(string a, string b)
{
    
}

int main()
{
    string a,b;
    cin >> a >> b;


    //Get next array part
    int j = 0, k = -1;
    int al = a.length(); int bl = b.length();

    int* next = new int[bl + 10];
    memset(next, 0 ,sizeof(next));


    next[0] = -1;
    while(j < bl)
    {
        if(k == -1 || b[j] == b[k])
        {
            j++;k++;
            next[j] = k;
        }
        else
        {
            k = next[k];//Change back to 0
        }
    }

    //Find string part
    int i = 0; j = 0;
    while(i < al && j < bl)
    {
        if(j == -1 || a[i] == b[j])
        {
            i++;j++;
        }
        else
            j = next[j];
    }
    
    //cout
    if(j >= bl)
        cout << i - bl << endl;
    else cout << "-1" << endl;


    for(i = 0; i < bl; i++)
        cout << next[i] << ((i == bl - 1) ? "" : " ");//
    cout << endl;
}