The data structure algorithm implemented in C language is explained one by one below:
(Swap function is a transposition function at the end, which can be understood)
1. Insert sorting
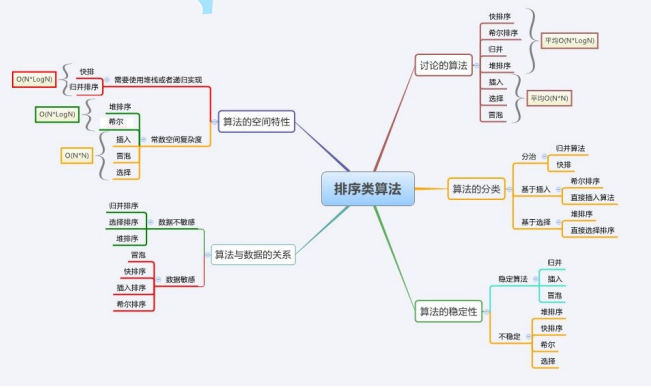
As the name suggests, a value is inserted one by one from the front. When inserting, it is sorted once. If there are n numbers, it is sorted n times
The idea is simple, so I won't introduce it. The code is as follows:
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
break;
}
a[end + 1] = tmp;
}
}Characteristics of direct sort insertion:
1. The closer the element set is to order, the higher the time efficiency of direct insertion sorting algorithm
2. Time complexity: O(N^2)
3. Space complexity: O(1)
4. Stability: stable (stability refers to the same value, and the latter value will not rank before the former value)
2. Hill sort
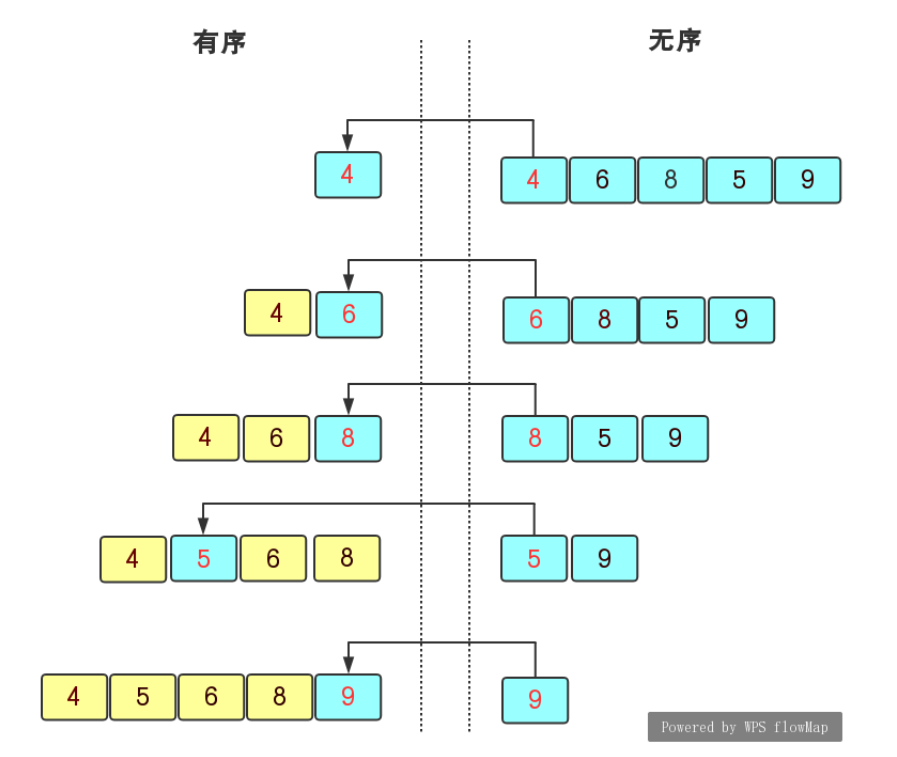
See my previous article for details. Hill sorting is to sort the values separated by gap to make them closer and closer to order, and finally end with gap small sorting with an interval of 1.
The code is as follows:
void ShellSort(int* a, int n)
{
int gap = n / 3 + 1; //Size by array length
while (gap > 1) //Jump out for the last time
{
for (int i = 0; i < n - gap; i++) //Using i + + can skillfully use multiple groups
{
int end = i;
int tmp = a[end + gap]; //Inserted value, gap apart
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap; //Forward comparison
}
else
break;
}
//When it is the smallest or encounters a value greater than it, the current position is assigned
a[end + gap] = tmp;
}
gap = gap / 3 + 1; //Gradual contraction
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
//Last move
for (int i = 0; i < n - 1; i++)
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= 1; //Forward comparison
}
else
break;
}
//When it is the smallest or encounters a value greater than it, the current position is assigned
a[end + 1] = tmp;
}
}Summary of Hill sort characteristics:
1. Hill sort is the optimization of direct insertion sort
2. When gap > 1, it is pre sorted to make the array closer to order. When gap == 1, the array is nearly ordered, so the optimization effect can be achieved
3. Time complexity: O(N^1.3-N^2), which is difficult to calculate and needs to be deduced
4. Space complexity: 0 (1)
5. Stability: unstable
3. Select Sorting
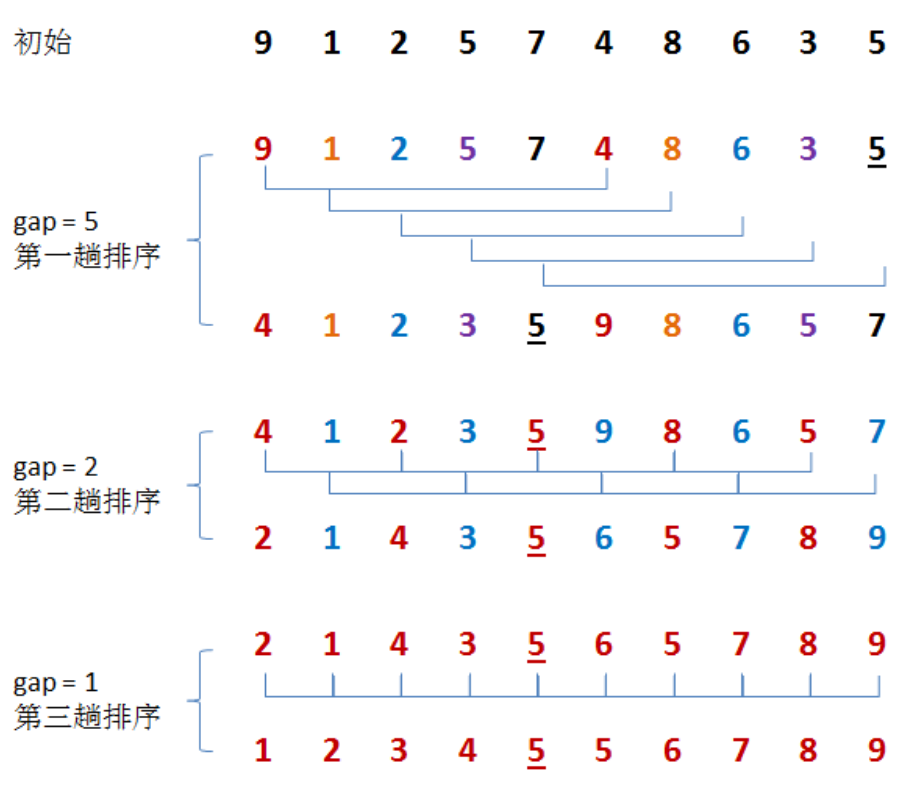
The idea of selecting sorting is:
First, traverse the array, find out the maximum and minimum values, and give them to the head and tail respectively. Then, the head + +, tail --, traverse the array again, change the head and tail, traverse, change the head and tail, until the head and tail pointers meet.
The code is as follows:
void SelectSort(int* a, int n)
{
int left = 0;
int right = n - 1;
while (left < right)
{
int minsort = left, maxsort = left;
for (int i = left; i <= right; i++)
{
if (a[i] > a[maxsort])
{
maxsort = i;
}
else if (a[i] < a[minsort])
{
minsort = i;
}
}
Swap(&a[left], &a[minsort]);
if (maxsort == left) //Judge that max gives the value of min
{
maxsort = minsort;
}
Swap(&a[right], &a[maxsort]);
left++;
right--;
}
}
Summary of characteristics of direct selection sorting:
1. Selection sorting is very easy to understand, but the efficiency is not very good, because it needs to be traversed all the time
2. Time complexity: O(N^2)
3. Space complexity: O(1)
4. Stability: unstable. In fact, sorting is unstable
4. Heap sorting
It is also easy to understand the sorting of large and small piles. Build a large pile in ascending order and a small pile in descending order. As long as the parent-child relationship is not destroyed, exchange the head and tail --n
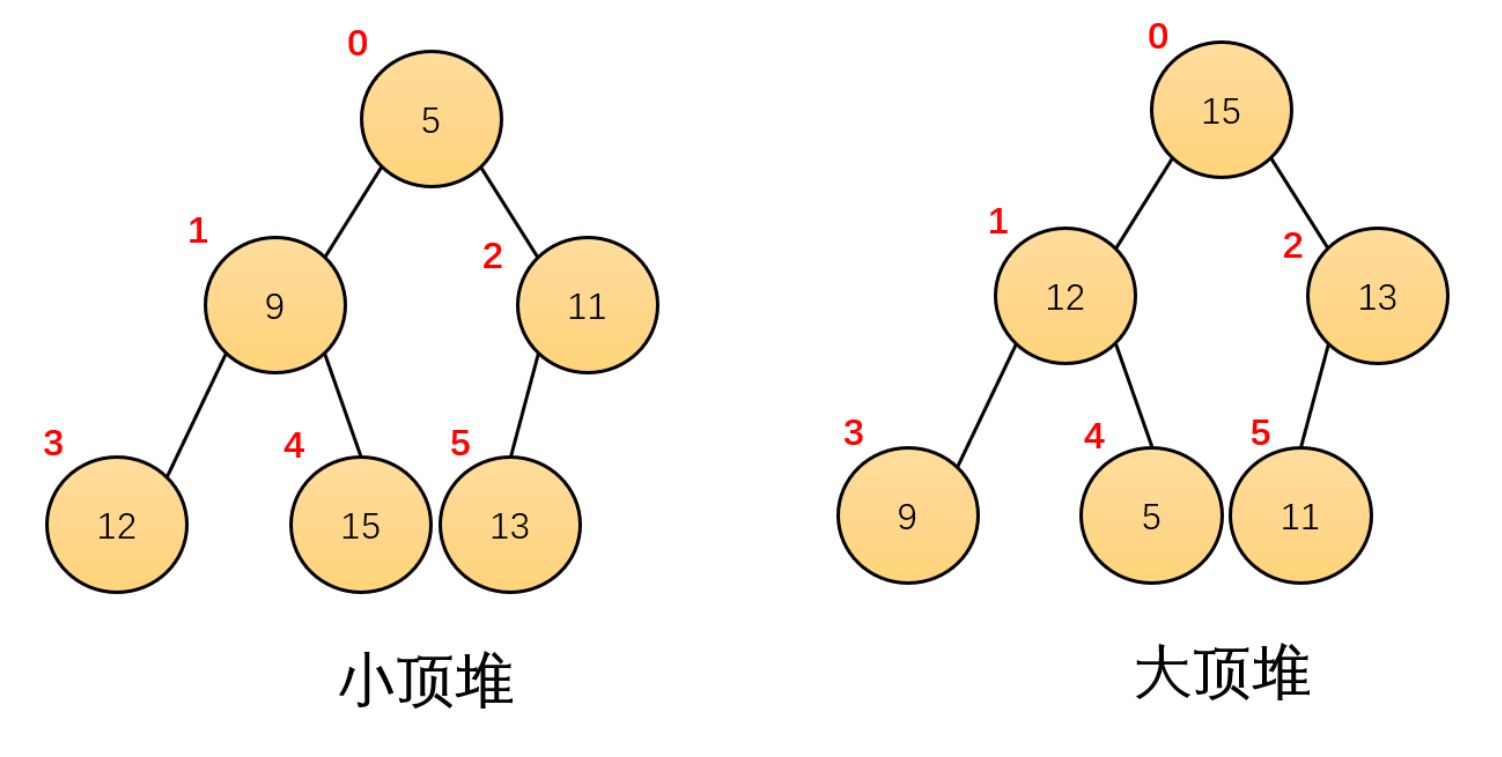
The code is as follows:
//Heap sort - sub
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child < n - 1 && a[child + 1] > a[child])
{
child++;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
//Heap sort - parent
void HeapSort(int* a, int n)
{
for (int i = (n - 1 - 1)/2; i >= 0; i--)
{
//Build pile
AdjustDown(a, n, i);
}
//It has been built
while (n > 0)
{
Swap(&a[0], &a[n - 1]);
AdjustDown(a, n - 1, 0);
n--;
}
}Summary of characteristics of direct selection sorting:
1. Heap sorting uses heap to select numbers, which is much more efficient
2. Time complexity: O(N*logN)
3. Space complexity: O(1)
4. Stability: unstable
5. Bubble sorting
The idea of bubble sorting is:
Traverse every digit from beginning to end, put the maximum (minimum) at the end, and then hide it.
Bubble sort is a sort of luck sort. If it is followed by order, you don't need to continue to traverse. If it is disordered, you need to do it one by one, which is longer than the time complexity of insertion sort. The reason for choosing is: the code is simple
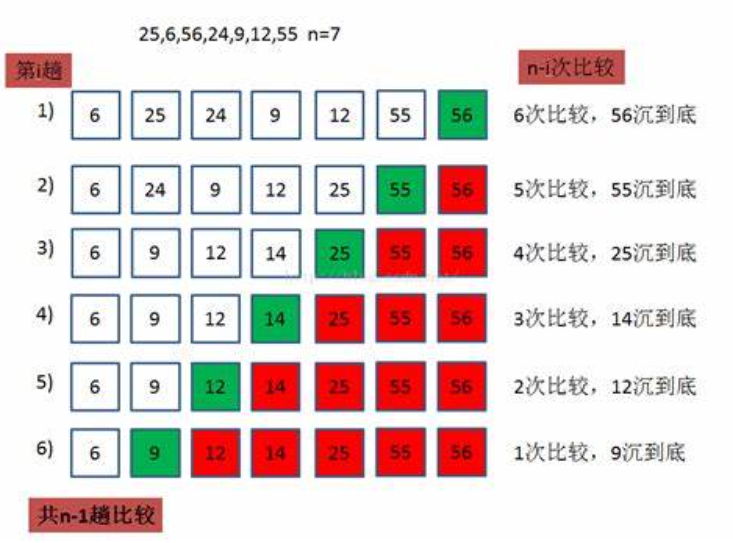
The code is as follows:
//Bubble sorting
void Bubble(int* a, int n)
{
for (int i = n - 1; i >= 0; i--)
{
int count = 0;
for (int j = 0; j < i; j++)
{
if (a[j] > a[j + 1])
{
int tmp = a[j];
a[j] = a[j + 1];
a[j + 1] = tmp;
count = 1;
}
}
if (count == 0)
break;
}
}
Summary of bubble sorting characteristics:
1. Easy to understand
2. Time complexity: O(N^2)
3. Space complexity: O(1)
4. Stability: stable
6. Quick sort
There are three types of fast platoon, which are commonly used:
1. hoare version 2 Excavation method # 3 Front and back pointer versions
First: hoare fast platoon
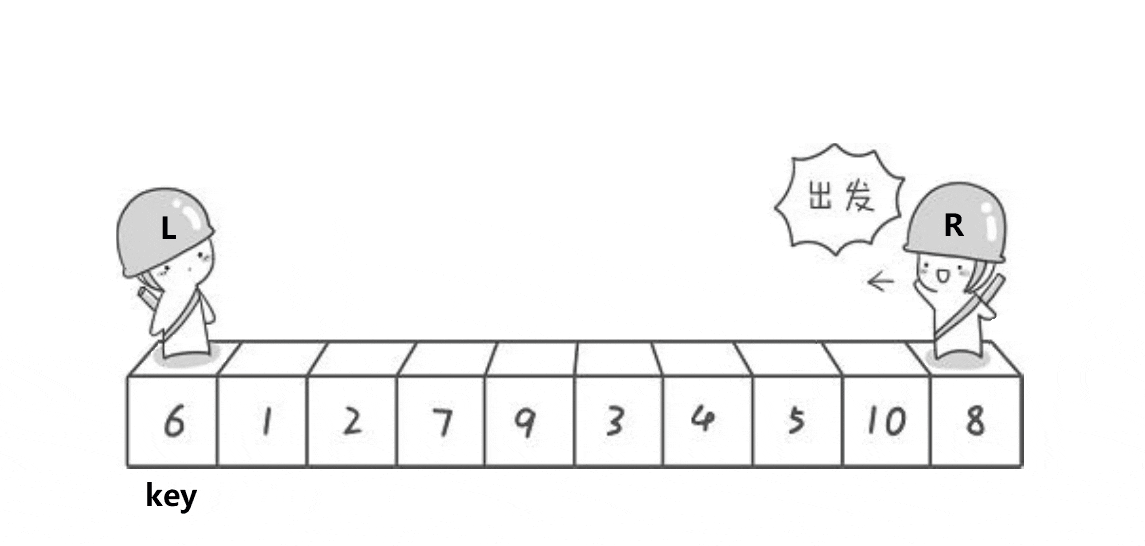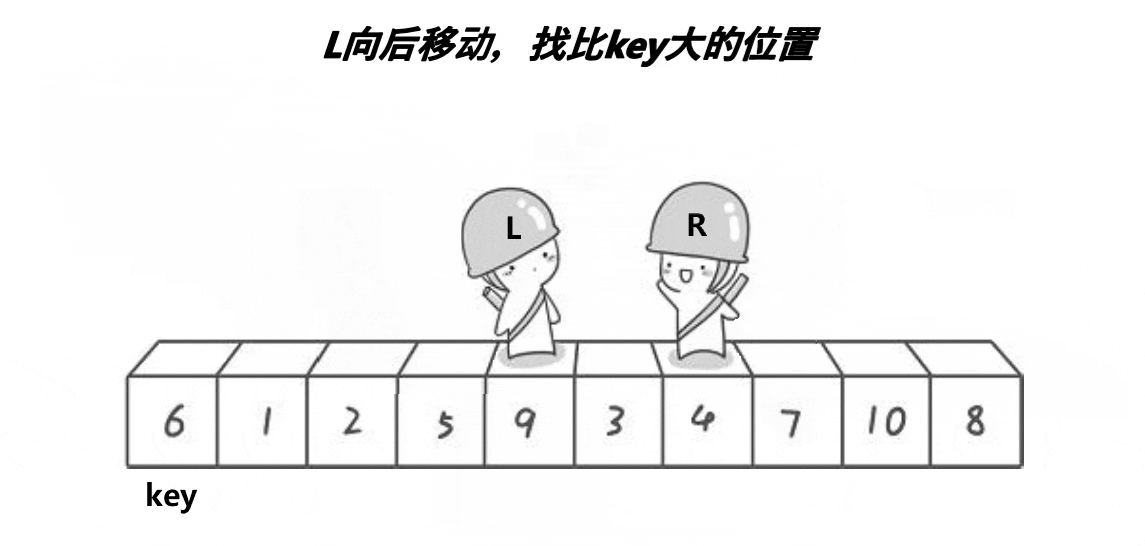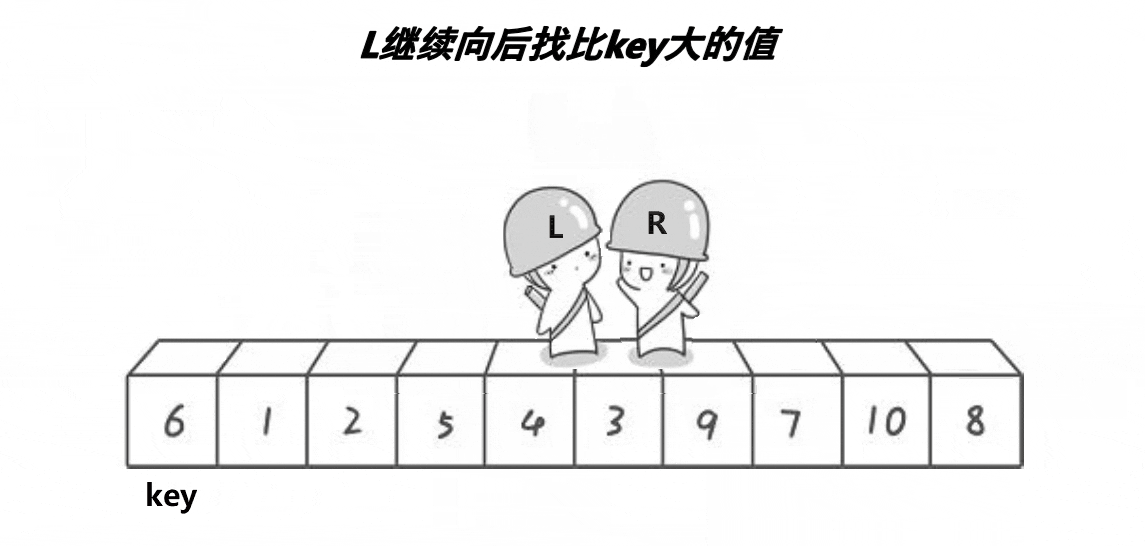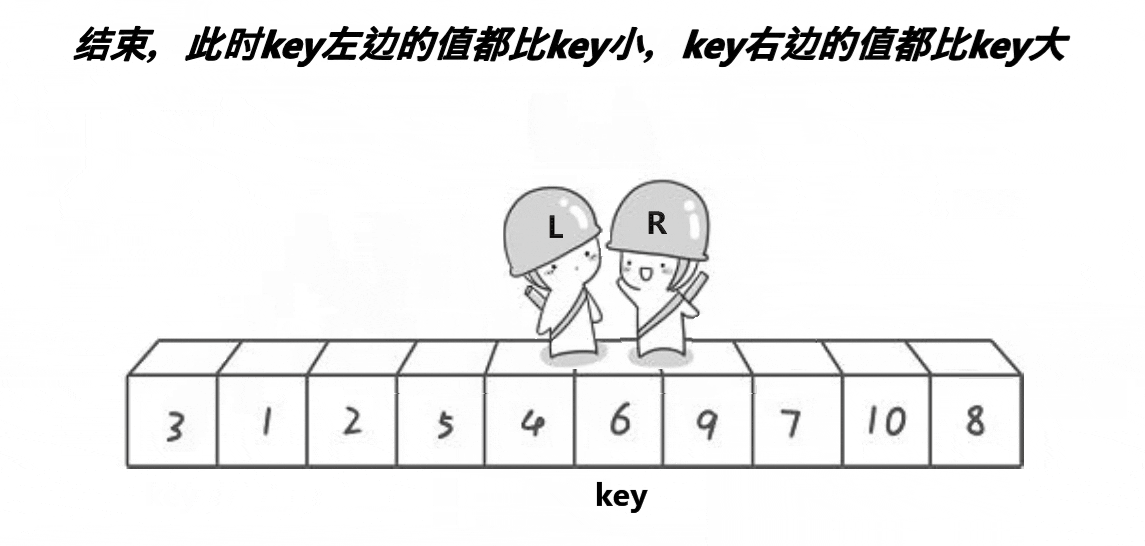
hoare's idea:
First, define left, right and key pointers. Left and right represent left and right respectively, and key represents the comparison value. Key points: if left is selected as key, let the right pointer go first. If right is selected as key, vice versa.
Right go first, stop at a position smaller than the key, go to left, stop at a position larger than the key, and then a[left] and a[right] exchange. Right continue to go and repeat until right and left intersect. Exchange the intersecting position meet with the value of the key. The given meet value can be used as recursive left and right.
The code is as follows:
int QuickHoare(int* a, int left, int right)
{
//Triple median method
int mid = GetKey(a, left, right);
Swap(&a[left], &a[mid]);
int key = left;
while (left < right)
{
//Move right first
while (left < right && a[right] >= a[key])
{
right--;
}
//Move to the left again
while (left < right && a[left] <= a[key])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[key], &a[left]);
//Come to the middle
int meet = left;
return meet;
}
Recursive functions are placed at the end of the fast queue.
The second method: excavation method
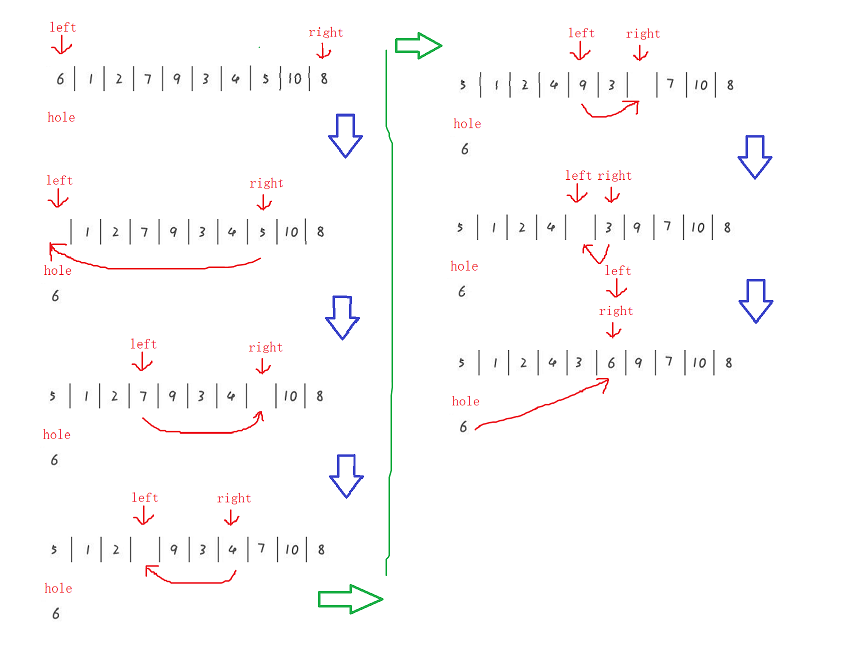
The idea of pit digging method:
left right hole pointer. As a hole, first take out the value of left and give it to hole, then right goes first, stops at a position larger than hole, and a[right] is directly given to a[left]. Because the value of left is given to hole at the beginning, there is no need to worry about being overwritten. Then left + +, stop when it is smaller than the hole, give a[left] to a[right], and then right --, assign, left + +, assign, know the intersection position of the two pointers, meet, and give the value of hole to meet.
The code is as follows:
int QuickDig(int* a, int left, int right)
{
//Dig a pit
int hole = a[left];
//sort
while (left < right)
{
//Go right first
while (left < right && a[right] >= hole)
right--;
a[left] = a[right]; //Pit filling
while (left < right && a[left] <= hole)
left++;
a[right] = a[left]; //Pit filling
}
a[left] = hole;
int meet = left;
return meet;
}The third method: front and back pointer method
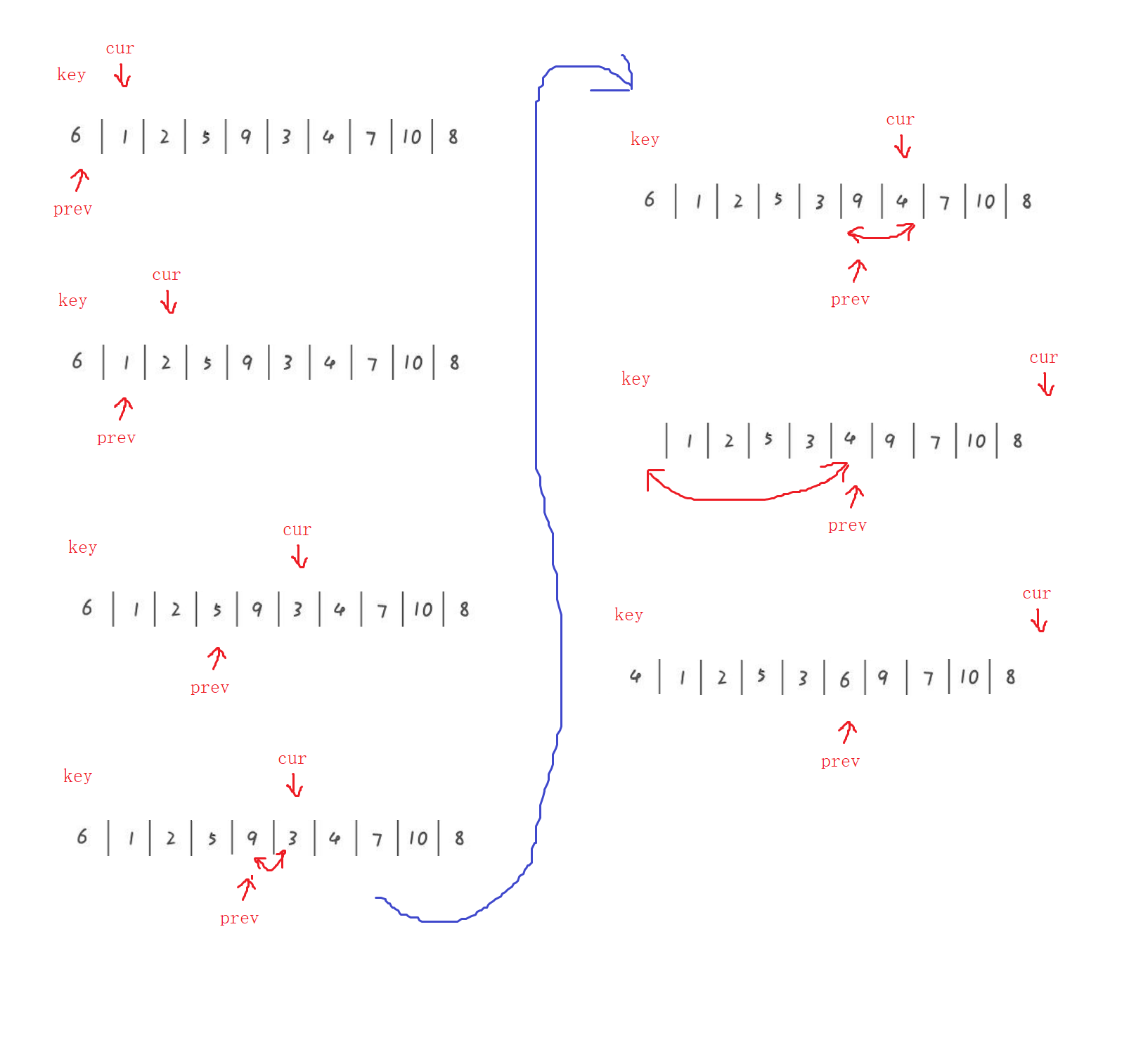
The idea of front and back pointer method:
Give a key prev cur pointer. Cur = prev + 1. The key stores the value where prev is located. If the value of cur is less than the value of key, cur and prev + 1 are exchanged. If cur encounters a value greater than key, it will be + +, until cur = right. Then key and prev are exchanged, and prev recurs as meet.
The code is as follows:
int QuickPoint(int* a, int left, int right)
{
int prev = left, cur = prev + 1;
//Triple median
//int mid = GetKey(a, left, right);
//Swap(&a[mid], &a[prev]);
int key = prev;
while (cur <= right)
{
if (a[key] > a[cur] && ++prev != cur) //Avoid in situ TP
{
Swap(&a[prev], &a[cur]);
}
cur++;
}
Swap(&a[key], &a[prev]);
return prev;
}Optimization code -- Code of three digit middle method:
int GetKey(int* a, int left, int right)
{
int mid = (left + right) >> 1; // Two values / 2
if (a[left] < a[mid]) // Left mid right which is in the middle
{
//left < mid ? right
if (a[mid] < a[right])
return mid;
else if (a[left] > a[right])
return left;
else
return right; // left < right < mid
}
else // (a[left] > a[mid])
{
//mid < left ? right
if (a[mid] > a[right])
return mid;
else if (a[left] < a[right])
return left;
else
return right;
}
}Recursive Code:
If you need to optimize, you can use three number centring and divide and conquer recursion
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
int keyi = QuickPoint(a, begin, end);
// [begin, keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
1,If there are more data in this sub interval, continue to select key Single pass, partition subinterval, divide and conquer recursion
2,If the data in this sub interval is small, it is not cost-effective to divide and conquer recursion
//if (end - begin > 20)
//{
// int keyi = QuickPoint(a, begin, end);
// // [begin, keyi-1] keyi [keyi+1, end]
// QuickSort(a, begin, keyi - 1);
// QuickSort(a, keyi + 1, end);
//}
//else
//{
// //HeapSort(a + begin, end - begin + 1);
// InsertSort(a + begin, end - begin + 1);
//}
}Summary of quick sort features:
1. You can always believe in fast platoon, fast platoon yyds!
2. Time complexity: O(N*logN)
3. Space complexity: O(logN)
4. Stability: unstable
7. Non recursive fast scheduling
Non recursive fast scheduling needs to use stack. Using the principle of stack, it is similar to recursion. If the interval is 0-10, put 0 and 10 for the first time; Put 0, 5, 6, 10 for the second time; Put 0, 5, 6, 8, 9, 10... For the third time... Every time we take the meet value, we have arranged the sequence. Then [6,10] has been arranged. Start the interval of [0,5], put 0, 2, 3, 5 first; Then go to 0, 2, 3, 4 and 5, and then take 4 and 5 as the left and right intervals to sort until they are arranged. Here, we need malloc a space to store the sorted values, and finally copy them to the original array and free them.
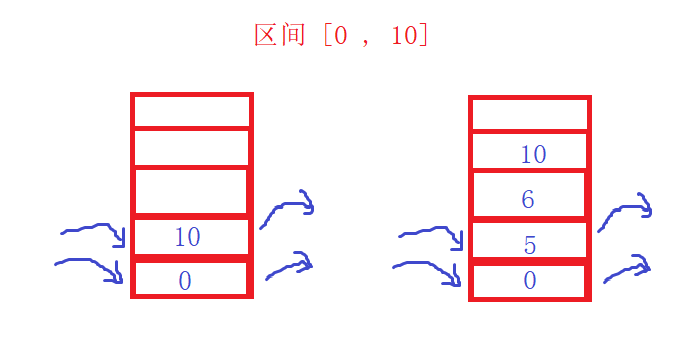
The code is as follows:
void QuickSortNonR(int* a, int left, int right)
{
stack st;
StackInit(&st);
//Save left and right range first
StackPush(&st, left);
StackPush(&st, right);
//If it is empty, the sorting is completed. If it is not empty, continue
while (!StackEmpty(&st))
{
int end = StackTop(&st);
StackPop(&st);
int begin = StackTop(&st);
StackPop(&st);
int key = QuickHoare(a, begin, end);
if (begin < key - 1)
{
StackPush(&st, begin);
StackPush(&st, key - 1);
}
if (end > key + 1)
{
StackPush(&st, key + 1);
StackPush(&st, end);
}
}
StackDistroy(&st);
}8. Merge and sort
The idea of merging and sorting:
Merging and sorting is essentially a process of dividing and ruling all the time. It splits the original array into small parts for comparison and sorting. In this way, each group of compared arrays is orderly. Only two pointers need to be created. left represents the head of the first group and right represents the head of the second group. Create a space. Whoever is small will put it in first. If which array ends first, The other group is directly added to the tail of the team, because it is orderly. Finally, it is copied to the original array and free is lost.
Enter the following code:
//Merge operation
void _Merge(int* a, int* tmp, int begin1, int end1, int begin2, int end2)
{
int i = begin1, j = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
for (; j <= end2; j++)
{
a[j] = tmp[j];
}
}
//Subfunction
void _MergeSort(int* a,int *tmp, int left, int right)
{
if (left >= right)
return;
int mid = (left + right) >> 1;
_MergeSort(a, tmp, left, mid);
_MergeSort(a, tmp, mid + 1, right);
int begin1 = left, begin2 = mid + 1, end1 = mid, end2 = right;
_Merge(a, tmp, begin1, end1, begin2, end2);
}
//Merge sort
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc false");
return;
}
int left = 0; int right = n - 1;
_MergeSort(a, tmp, left, right);
free(tmp);
}Summary of characteristics of merging and sorting:
1. The disadvantage of merging is that it requires O(N) space complexity. The thinking of merging sorting is more to solve the problem of external sorting in the disk.
2. Time complexity: O(N*logN)
3. Space complexity: O(N)
4. Stability: stable
9. Non recursive merge sort
There are many requirements for non recursive merging. First look at the code:
//Merge operation
void _Merge(int* a, int* tmp, int begin1, int end1, int begin2, int end2)
{
int i = begin1, j = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
for (; j <= end2; j++)
{
a[j] = tmp[j];
}
}
//Non recursive merge sort
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc false");
return;
}
int left = 0, right = n - 1;
int gap = 1; //The interval is 1, and then increase later
while (gap < n)
{
for (int j = 0; j < right; j += gap*2)
{
//[j, j+gap-1] [j+gap, j+gap*2-1]
int begin1 = j, begin2 = j + gap, end1 = j + gap - 1, end2 = j + gap * 2 - 1;
//Consider multiple situations
//Before and after the interval is less than 1
if (end1 >= right)
break;
//2. There is a front interval, but the rear interval is less than right
if (end2 > right)
{
end2 = right;
}
_Merge(a, tmp, begin1, end1, begin2, end2);
}
gap *= 2;
}
}
What's complicated here is_ For the values of the two intervals before and after the Merge function, we need to pay attention not to allow end1 or end2 to cross the boundary. The gap is * = 2 each time and j = gap*2. Considering the three states, it may end in half and the latter half has not entered. The conditions of 1 and 3 in the figure can be the same, because there is no rear interval, so it is not implemented at all.
Sort, count
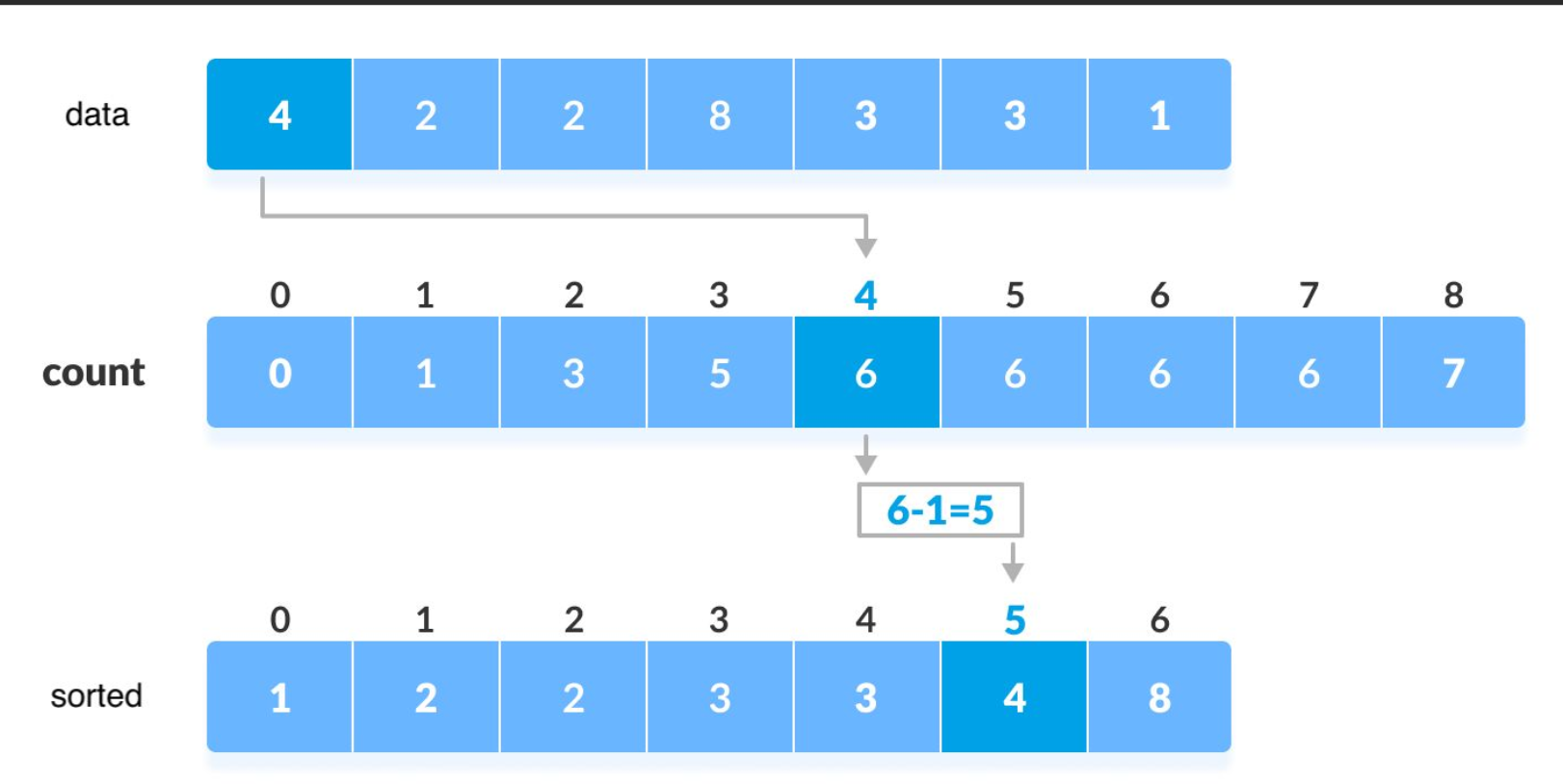
Counting sorting is actually very simple. It involves a mapping problem
The idea of counting and sorting:
Create an array. The subscript of the array corresponds to the value of the array to be sorted. For example, in the above figure, 4 in data is placed in the subscript of 4 in count. At this time, the subscript + 1. If there are three 6, the [6] of count is equal to 3, which means that there are three 6. Similarly, 1 puts 1, 2 puts 2, and one puts + 1. Finally, print three 6's according to the value of subscript count[6] = 3.
Because it is an absolute mapping, there may be a waste of space. For example, the minimum value of data is 1000 and the maximum value is 1001. Do you want to create [01001]?! Therefore, we need to use relative mapping here. First traverse the array to find the maximum and minimum values. The minimum value is the mapped value, and the subsequent addition and subtraction only need + - minimum value min.
The code is as follows:
void CountSort(int* a, int n)
{
int gap = 0, min = a[0], max = a[0];
for (int i = 0; i < n; i++)
{
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
//Find the difference between the maximum value and the minimum value, and make a relative mapping
gap = max - min + 1;
int* count = (int*)malloc(sizeof(int) * gap);
memset(count, 0 ,sizeof(int) * gap);
//Mark on count
for (int i = 0; i < n; i++)
{
count[a[i] - min]++;
}
//Assign back
int i = 0;
for (int j = 0; j < gap; j++)
{
while (count[j]--)
{
a[i++] = j + min;
}
}
free(count);
}Summary of characteristics of count sorting:
1. When the counting sorting is in the data range set, the efficiency is very high, but the scope of application and scenarios are limited
2. Time complexity: O(MAX(N, range))
3. Space complexity: O (range)
4. Stability: stable
Summary: