https://www.bilibili.com/video/BV1E4411H73v?p=6
Data structures include linear and non-linear structures.
Linear structure:
-
As the most common data structure, linear structure is characterized by one-to-one linear relationship among data elements.
-
Linear structures have two different storage structures, sequential storage (array) and chain storage (chain table). A linear table with a sequential storage structure is called a sequential table, and the storage elements in the sequential table are continuous.
-
A linear table with chain storage is called a chain table. Stored elements in a chain table are not necessarily continuous. Data elements and address information of adjacent elements are stored in element nodes.
-
Linear structures are common: arrays, queues, chained lists, and stacks.
Nonlinear structure:
- Nonlinear structures include two-dimensional arrays, multidimensional arrays, generalized tables, tree structures, and graph structures.
1. Sparse Arrays and Queues
1. Sparse Array

Basic Introduction:
Sparse arrays can be used to save an array when most of the elements in the array are 0 or the same value.
Processing methods for sparse arrays:
- The record array has rows, columns, and different values.
- Reduce the size of the program by recording rows, columns, and values of elements with different values in a small array.
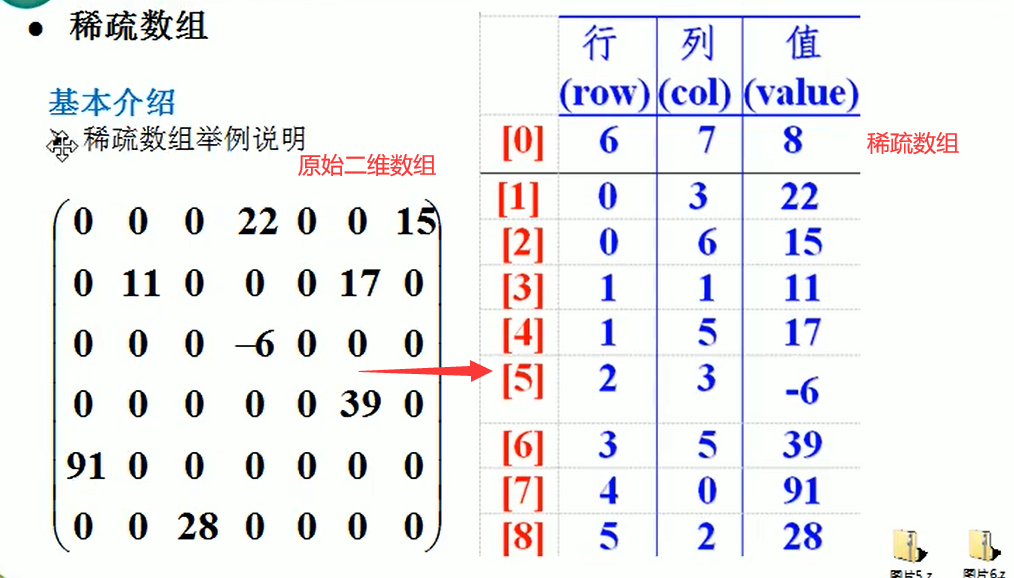
As shown in the figure, a two-dimensional array of 6X7 is turned into a sparse array of 9X3. among
- The first row holds the rows and columns of the original two-dimensional array and the number of non-zero values
- Lines 2 through 9 hold the location and value of each non-zero value
Train of thought:
Two-dimensional array to sparse array:
- Traverse the original two-dimensional array, sum the number of valid data
- Create a sparse array with sum+1 rows and 3 columns (fixed)
- Store valid values from a two-dimensional array in a sparse array
Sparse arrays to two-dimensional arrays:
- Read the first row of a sparse array to create the original two-dimensional array from the first row of data
- Reads the data in the last few rows of a sparse array and assigns values to the number in the corresponding position of the two-dimensional array
Code:
public static void main(String[] args) {
//Create a two-dimensional array
int[][] arr1 = new int[11][11];
//Put values into a two-dimensional array
arr1[1][2] = 1;
arr1[2][3] = 2;
arr1[3][4] = 3;
//Print 2-D Array
System.out.println("Traversing a two-dimensional array");
for (int i = 0; i < arr1.length; i++) {
for (int j = 0; j < arr1[0].length; j++) {
System.out.print(arr1[i][j] + " ");
}
System.out.println();
}
//Binary Array----->Sparse Array
//Traverse the number of valid values in a two-dimensional array, and record with sum
int sum = 0;
for (int i = 0; i < arr1.length; i++) {
for (int j = 0; j < arr1[0].length; j++) {
if (arr1[i][j] != 0) {
//A valid value is an element in a two-dimensional array that is not zero
sum++;
}
}
}
//Create Sparse Array
//The number of rows is sum+1. The first row holds the number of rows, columns, and valid values of the two-dimensional array. The number of columns is fixed to 3.
int[][] sparseArr = new int[sum + 1][3];
//Rows and columns stored in a two-dimensional array and the number of valid values
sparseArr[0][0] = arr1.length;
sparseArr[0][1] = arr1[0].length;
sparseArr[0][2] = sum;
//Traverse the two-dimensional array again to save valid values into the sparse array
//Number of rows to save a sparse array
int count = 1;
for (int i = 0; i < arr1.length; i++) {
for (int j = 0; j < arr1[0].length; j++) {
if (arr1[i][j] != 0) {
//Save values in a sparse array
sparseArr[count][0] = i;
sparseArr[count][1] = j;
sparseArr[count][2] = arr1[i][j];
count++;
}
}
}
//Print sparse array
System.out.println("Traversing sparse arrays");
for (int i = 0; i < sparseArr.length; i++) {
for (int j = 0; j < sparseArr[0].length; j++) {
System.out.print(sparseArr[i][j] + " ");
}
System.out.println();
}
//Sparse Array----> Two-dimensional Array
//Get the number of rows and columns of the binary array first
int row = sparseArr[0][0];
int col = sparseArr[0][1];
int[][] arr2 = new int[row][col];
//Traverse sparse arrays while assigning values to two-dimensional arrays
for (int i = 1; i < sparseArr.length; i++) {
row = sparseArr[i][0];
col = sparseArr[i][1];
//The corresponding value at that location
int val = sparseArr[i][2];
arr2[row][col] = val;
}
//Print 2-D Array
System.out.println("Traversing the restored two-dimensional array");
for (int i = 0; i < arr2.length; i++) {
for (int j = 0; j < arr2[0].length; j++) {
System.out.print(arr2[i][j] + " ");
}
System.out.println();
}
}
Run result:
Traversing a two-dimensional array 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Traversing sparse arrays 11 11 3 1 2 1 2 3 2 3 4 3 Traversing the restored two-dimensional array 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2. Queues
Definition
- A queue is an ordered list that can be implemented as an array or a list of chains.
- Follow the FIFO principle. That is, the data stored in the queue is taken out first. Post-Saved To-Remove
Array simulation queue
- The queue itself is a sequential table. If the structure of the array is used to store the data of the queue, the declaration of the queue array is shown below, where maxSize is the maximum capacity of the queue
- Because the output and input of a queue are processed from the front and back ends, two variables, front and rear, are required to record the subscripts of the front and back ends of the queue. Front changes with the output of the data, while rear changes with the input of the data, as shown in the figure.
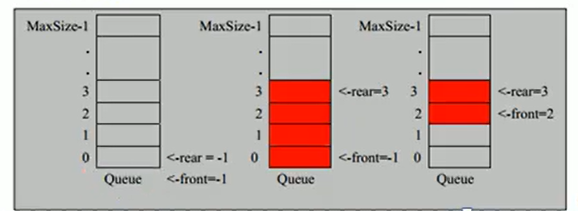
Simulation of Entry and Queue Operation
When we queue data, we call it "addQueue", and addQueue processing takes two steps:
- Move the tail pointer backward: rear+1, when front == rear, the queue is empty
- If the tail pointer rear is less than the maximum subscript maxSize-1 of the queue, the data is stored in the array element referred to by the rear, otherwise it cannot be stored. When rear == maxSize - 1, the queue is full
Note: front points to the previous position of the first element of the queue
Code
public class Demo3 {
public static void main(String[] args) {
ArrayQueue queue = new ArrayQueue(5);
queue.addNum(1);
queue.addNum(2);
queue.addNum(3);
queue.addNum(4);
queue.addNum(5);
System.out.println(queue.getNum());
queue.showQueue();
}
}
class ArrayQueue {
//Queue size
int maxSize;
//Using arrays to implement queues
int[] arr;
//Point to the previous position of the first element of the queue
int front;
//End element pointing to queue
int rear;
public ArrayQueue(int maxSize) {
this.maxSize = maxSize;
arr = new int[this.maxSize];
//front points to the previous position of the first element of the queue
front = -1;
rear = -1;
}
public boolean isFull() {
return rear == maxSize - 1;
}
public boolean isEmpty() {
return front == rear;
}
public void addNum(int num) {
if(isFull()) {
System.out.println("The queue is full and cannot be enqueued");
return;
}
//The end tag moves backwards, pointing to the location of the element to be placed
rear++;
arr[rear] = num;
}
public int getNum() {
if(isEmpty()) {
throw new RuntimeException("Queue empty, unable to leave");
}
//Head tag moved back, pointing to the header element
System.out.print("The queue elements are:");
front++;
return arr[front];
}
public void showQueue() {
if(isEmpty()) {
throw new RuntimeException("Queue is empty and cannot be traversed");
}
System.out.println("Traverse Queue");
//Read elements from front+1
for(int start = front+1; start<=rear; start++) {
System.out.println(arr[start]);
}
}
}
Run result:
The queue elements are:1 Traverse Queue 2 3 4 5
Ring Queue
Ideas:
- The front variable points to the queue head element with an initial value of 0
- The rear variable points to the next element of the queue tail element, and the rear initial value is 0. Provide a space for
- The criteria for determining the queue is empty: front == rear [empty]
- The criteria for a full queue: (rear + 1)% maxSize == front [full]
- Number of valid elements in queue: (rear + maxSize-front)% maxSize
- Markers need to be modeled for maxSize when entering or leaving the team

Code:
public class Demo4 {
public static void main(String[] args) {
ArrayAroundQueue aroundQueue = new ArrayAroundQueue(5);
aroundQueue.addNum(1);
aroundQueue.addNum(2);
aroundQueue.addNum(3);
aroundQueue.addNum(4);
int size = aroundQueue.size();
System.out.println("size:"+size);
aroundQueue.showQueue();
System.out.println(aroundQueue.getNum());
System.out.println(aroundQueue.getNum());
aroundQueue.addNum(5);
aroundQueue.addNum(6);
aroundQueue.showQueue();
aroundQueue.getHead();
}
}
class ArrayAroundQueue {
//Queue size
int maxSize;
//Using arrays to implement queues
int[] arr;
//Point to the previous position of the first element of the queue
int front;
//End element pointing to queue
int rear;
public ArrayAroundQueue(int maxSize) {
this.maxSize = maxSize;
arr = new int[this.maxSize];
//front points to the previous position of the first element of the queue
front = 0;
rear = 0;
}
public boolean isFull() {
return (rear+1)%maxSize == front;
}
public boolean isEmpty() {
return front == rear;
}
public void addNum(int num) {
if(isFull()) {
System.out.println("The queue is full and cannot be enqueued");
return;
}
//Add data directly
arr[rear] = num;
//Move the rear backward, where modulo must be considered
rear = (rear+1)%maxSize;
}
public int getNum() {
if(isEmpty()) {
throw new RuntimeException("Queue empty, unable to leave");
}
//Head tag moved back, pointing to the header element
System.out.print("The queue elements are:");
int num = arr[front];
//Move the front backward, considering modelling
front = (front+1)%maxSize;
return num;
}
public void showQueue() {
if(isEmpty()) {
throw new RuntimeException("Queue is empty and cannot be traversed");
}
System.out.println("Traverse Queue");
//Stop traversal when front + 1 == rear
int start = front;
while(start != rear) {
System.out.println(arr[start]);
//Move to the next element
start = (start+1)%maxSize;
}
}
public void getHead() {
if(isEmpty()) {
throw new RuntimeException("Queue empty");
}
System.out.println("The first element of the queue is:"+arr[front]);
}
//Find the number of valid data for the current queue
public int size() {
return ( rear + maxSize - front) % maxSize;
}
}
Run result:
size4 Traverse Queue 1 2 3 4 The queue elements are:1 The queue elements are:2 Traverse Queue 3 4 5 6 The first element of the queue is:3
Chain List
1. One-way Chain List
Chain List Introduction
A chain table is an ordered list, but it is stored in memory as follows:
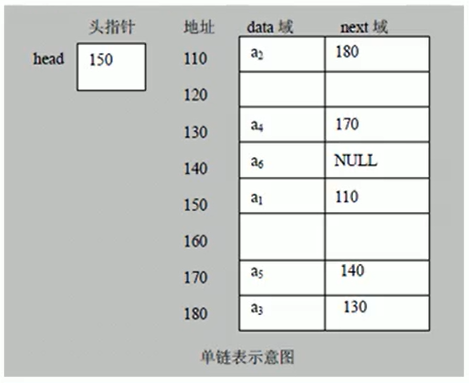
Characteristic
- Chain lists are stored as nodes and as chains
- Each node contains a data field and a next field. The next field is used to point to the next node
- The nodes of a chain table are not necessarily stored continuously
- The list of chains with and without a header node, which is determined according to the actual requirements
Schematic Diagram with Head Nodes
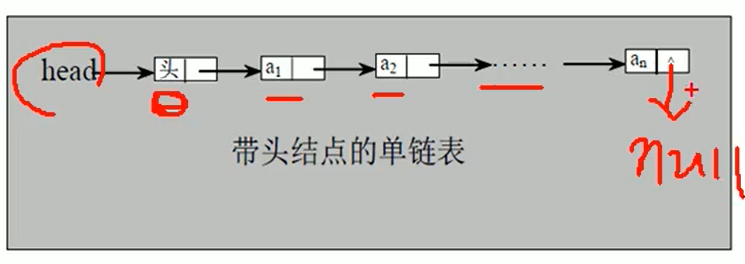

Ideas for implementation
Create (Add)
- Create a Head Header node to represent the header of a single-chain table
- Later, as each node is added, it is placed at the end of the list of chains
ergodic
- Traverse the entire list of chains through an auxiliary variable
Ordered Insertion
- Walk through the list to find where you should insert it
- New node. next = temp.next
- Will temp.next = new node
Modify values based on an attribute node
- Walk through the nodes first to find the modified location
- If no modification node is found, do not modify

Delete a node
- Traverse through the node first to find the previous node temp to delete the node
- temp.next = temp.next.next
- Deleted nodes will not have other reference points and will be recycled by the garbage collection mechanism
Find information for the nth last node
- Traverse the list of chains to find the effective length of the list (not counting as the head node)
- Traverse the link list to the length-n node
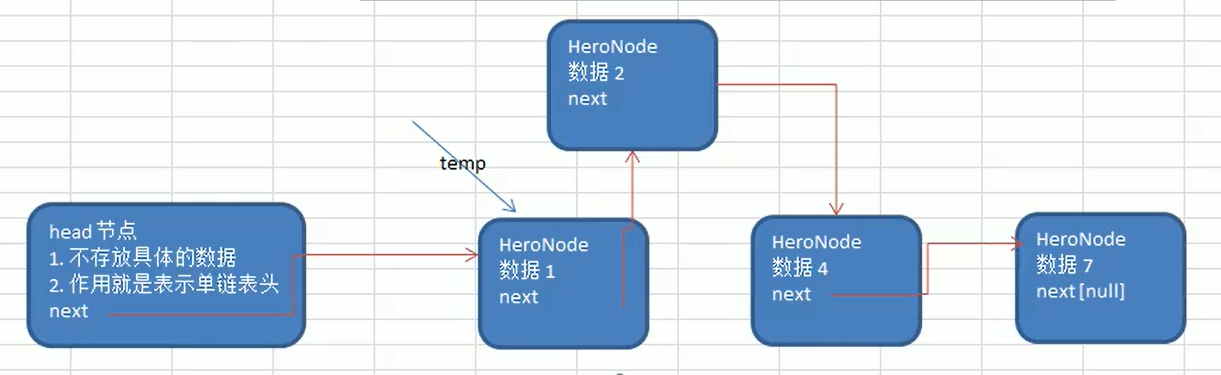
Flip Chain List
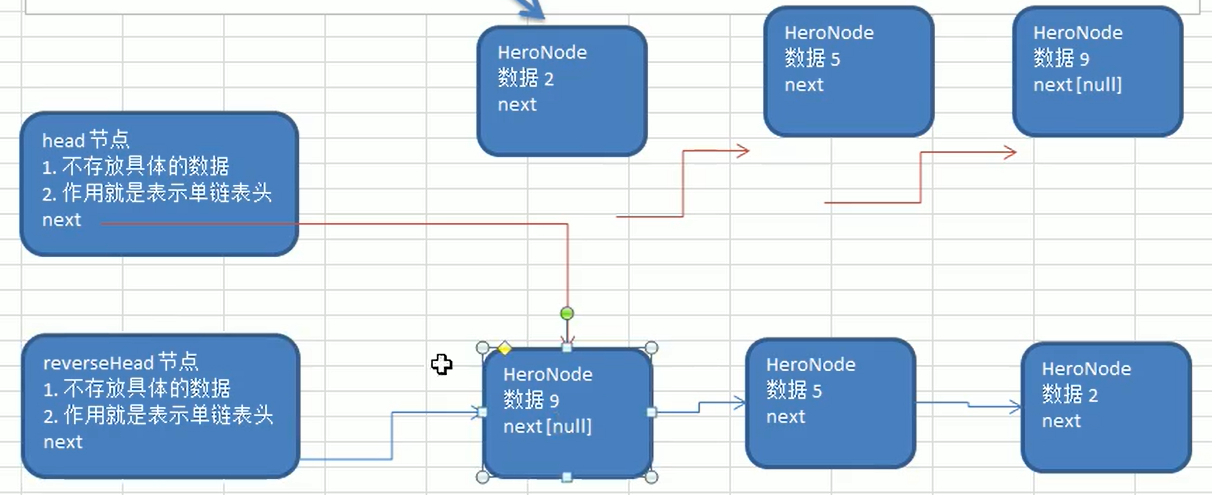


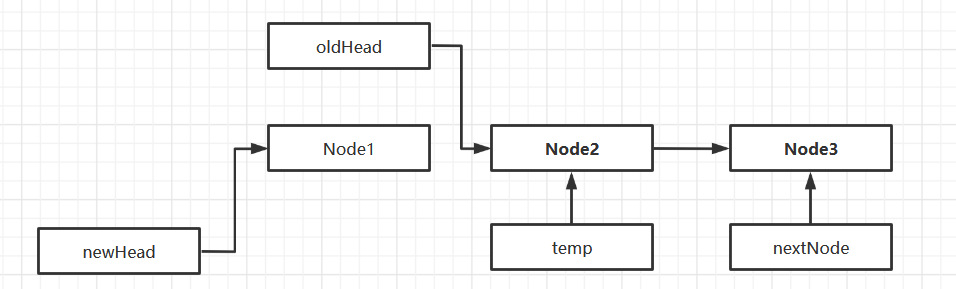
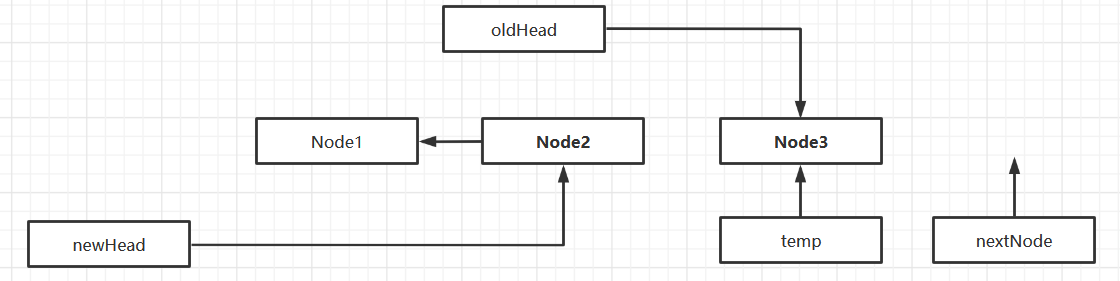
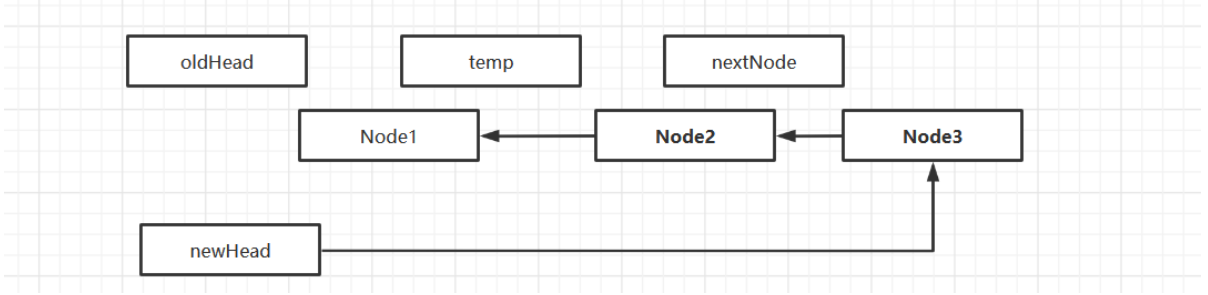
Create a new header node as the header of the new chain table
-
Walk through the old list from scratch, inserting the traversed node after the header node of the new list
-
Note that needs to be used
Two staging nodes
- A node to save traversing
- One to hold the next node that is traversing the node
Print in reverse order
- Traverse the list of chains to Stack the traversed nodes
- After traversal, stack out and print out stack elements
Code:
public class lianbiao {
public static void main(String[] args) {
SingleLinkedList linkedList = new SingleLinkedList();
linkedList.traverseNode();
System.out.println();
//Create a student node and insert a chain table
StudentNode student1 = new StudentNode(1, "Nyima");
StudentNode student3 = new StudentNode(3, "Lulu");
linkedList.addNode(student1);
linkedList.addNode(student3);
linkedList.traverseNode();
System.out.println();
//Insert by id size
System.out.println("Ordered Insertion");
StudentNode student2 = new StudentNode(0, "Wenwen");
linkedList.addByOrder(student2);
linkedList.traverseNode();
System.out.println();
//Modify student information by id
System.out.println("Modify Student Information");
student2 = new StudentNode(1, "Hulu");
linkedList.changeNode(student2);
linkedList.traverseNode();
System.out.println();
//Delete student information based on id
System.out.println("Delete Student Information");
student2 = new StudentNode(1, "Hulu");
linkedList.deleteNode(student2);
linkedList.traverseNode();
System.out.println();
//Get the last node
System.out.println("Get the reciprocal node");
System.out.println(linkedList.getStuByRec(2));
System.out.println();
//Flip Chain List
System.out.println("Flip Chain List");
SingleLinkedList newLinkedList = linkedList.reverseList();
newLinkedList.traverseNode();
System.out.println();
//Recursive Traversal Chain List
System.out.println("Reverse Traversal Chain List");
newLinkedList.reverseTraverse();
}
}
/**
* Create Chain List
*/
class SingleLinkedList {
//Head node, prevent modification, set to private
private StudentNode head = new StudentNode(0, "");
/**
* Add Node
* @param node Node to add
*/
public void addNode(StudentNode node) {
//Create a secondary node because the header node cannot be modified
StudentNode temp = head;
//Find the last node
while (true) {
//Stop looping if temp is the tail node
if(temp.next == null) {
break;
}
//Move backward without end
temp = temp.next;
}
//Now temp is the end node, insert it again
temp.next = node;
}
/**
* Traversing a list of chains
*/
public void traverseNode() {
System.out.println("Start traversing the list of chains");
if(head.next == null) {
System.out.println("Chain list is empty");
}
//Create secondary nodes
StudentNode temp = head.next;
while(true) {
//Stop loop when traversal is complete
if(temp == null) {
break;
}
System.out.println(temp);
temp = temp.next;
}
}
/**
* Insert nodes in id order
* @param node
*/
public void addByOrder(StudentNode node) {
//If there is no first node, insert it directly
if(head.next == null) {
head.next = node;
return;
}
//Secondary node, used to find insertion location and insertion operation
StudentNode temp = head;
//The next node of the node exists, and its id is less than the id of the node to be inserted, it continues to move down
while (temp.next!=null && temp.next.id < node.id) {
temp = temp.next;
}
//Do this if the next node of temp exists
//And insert operation, order cannot be changed
if(temp.next != null) {
node.next = temp.next;
}
temp.next = node;
}
/**
* Modify node information based on id
* @param node Nodes that modify information
*/
public void changeNode(StudentNode node) {
if(head == null) {
System.out.println("The list is empty, Please add the student information first");
return;
}
StudentNode temp = head;
//Traverse the list of chains to find the node you want to modify
while (temp.next!= null && temp.id != node.id) {
temp = temp.next;
}
//If temp is already the last node, determine if IDs are equal
if(temp.id != node.id) {
System.out.println("No information was found for the student, please create the student's information first");
return;
}
//Modify Student Information
temp.name = node.name;
}
/**
* Delete nodes based on id
* @param node Node to delete
*/
public void deleteNode(StudentNode node) {
if(head.next == null) {
System.out.println("Chain list is empty");
return;
}
StudentNode temp = head.next;
//Traverse the list to find the node to delete
if(temp.next!=null && temp.next.id!=node.id) {
temp = temp.next;
}
//Determine if the last node is to be deleted
if(temp.next.id != node.id) {
System.out.println("Please insert the student information first");
return;
}
//Delete this node
temp.next = temp.next.next;
}
/**
* Get the reciprocal node
* @param index Last Number
* @return
*/
public StudentNode getStuByRec(int index) {
if(head.next == null) {
System.out.println("Chain list is empty!");
}
StudentNode temp = head.next;
//User records the length of the list because head.next is not empty, there is already a node
//So length is initialized to 1
int length = 1;
while(temp.next != null) {
temp = temp.next;
length++;
}
if(length < index) {
throw new RuntimeException("Chain list out of bounds");
}
temp = head.next;
for(int i = 0; i<length-index; i++) {
temp = temp.next;
}
return temp;
}
/**
* Flip Chain List
* @return Inverted Chain List
*/
public SingleLinkedList reverseList() {
//Chain list is empty or has only one node and does not need to be flipped
if(head.next == null || head.next.next == null) {
System.out.println("No need to flip");
}
SingleLinkedList newLinkedList = new SingleLinkedList();
//Create a new header node for a new list
newLinkedList.head = new StudentNode(0, "");
//Used to save the node being traversed
StudentNode temp = head.next;
//Used to save the next node of the node being traversed
StudentNode nextNode = temp.next;
while(true) {
//Insert New Chain List
temp.next = newLinkedList.head.next;
newLinkedList.head.next = temp;
//Move to Next Node
temp = nextNode;
nextNode = nextNode.next;
if(temp.next == null) {
//Insert Last Node
temp.next = newLinkedList.head.next;
newLinkedList.head.next = temp;
head.next = null;
return newLinkedList;
}
}
}
public void reverseTraverse() {
if(head == null) {
System.out.println("Chain list is empty");
}
StudentNode temp = head.next;
//Create a stack to hold traversed nodes
Stack<StudentNode> stack = new Stack<>();
while(temp != null) {
stack.push(temp);
temp = temp.next;
}
while (!stack.isEmpty()) {
System.out.println(stack.pop());
}
}
}
/**
* Define Nodes
*/
class StudentNode {
int id;
String name;
//Address to save the next node
StudentNode next;
public StudentNode(int id, String name) {
this.id = id;
this.name = name;
}
@Override
public String toString() {
return "StudentNode{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
}
Output:
Start traversing the list of chains
Chain list is empty
Start traversing the list of chains
StudentNode{id=1, name='Nyima'}
StudentNode{id=3, name='Lulu'}
Ordered Insertion
Start traversing the list of chains
StudentNode{id=0, name='Wenwen'}
StudentNode{id=1, name='Nyima'}
StudentNode{id=3, name='Lulu'}
Modify Student Information
Start traversing the list of chains
StudentNode{id=0, name='Wenwen'}
StudentNode{id=1, name='Hulu'}
StudentNode{id=3, name='Lulu'}
Delete Student Information
Start traversing the list of chains
StudentNode{id=0, name='Wenwen'}
StudentNode{id=3, name='Lulu'}
Get the reciprocal node
StudentNode{id=0, name='Wenwen'}
Flip Chain List
Start traversing the list of chains
StudentNode{id=3, name='Lulu'}
StudentNode{id=0, name='Wenwen'}
Reverse Traversal Chain List
StudentNode{id=0, name='Wenwen'}
StudentNode{id=3, name='Lulu'}
Process finished with exit code 0
2. Bidirectional Chain List

Ideas for implementation
ergodic
- The same traversal as a one-way chain table, except that you can look forward or backward
Add Default to Last of Bi-directional Chain List
- Find the last node of the two-way list first
- temp.next = newHeroNode;
- newHeroNode.pre = temp;
modify
- Same modification as one-way list
delete
- Use temp to save nodes to delete
- temp.pre.next points to temp.next
- temp.next.pre points to temp.pre
Code:
public class shuangxianglianbiao {
public static void main(String[] args) {
BidirectionalList bidirectionalList = new BidirectionalList();
bidirectionalList.addNode(new PersonNode(1, "Nyima"));
bidirectionalList.addNode(new PersonNode(2, "Lulu"));
bidirectionalList.traverseNode();
System.out.println();
System.out.println("Modify Node Information");
bidirectionalList.changeNode(new PersonNode(2, "Wenwen"));
bidirectionalList.traverseNode();
System.out.println();
//Delete Node
System.out.println("Delete Node");
bidirectionalList.deleteNode(new PersonNode(1, "Nyima"));
bidirectionalList.traverseNode();
}
}
class BidirectionalList {
private final PersonNode head = new PersonNode(-1, "");
/**
* Determine if the two-way chain table is empty
* @return Null result
*/
public boolean isEmpty() {
return head.next == null;
}
/**
* Add will point
* @param node Node to be added
*/
public void addNode(PersonNode node) {
PersonNode temp = head;
if(temp.next != null) {
temp = temp.next;
}
//Insert after last node
temp.next = node;
node.front = temp;
}
public void traverseNode() {
System.out.println("Traversing a list of chains");
if (isEmpty()) {
System.out.println("Chain list is empty");
return;
}
PersonNode temp = head.next;
while(temp != null) {
System.out.println(temp);
temp = temp.next;
}
}
/**
* Modify Node Information
* @param node Node to Modify
*/
public void changeNode(PersonNode node) {
if(isEmpty()) {
System.out.println("Chain list is empty");
return;
}
PersonNode temp = head.next;
//Used to determine whether changes have been made
boolean flag = false;
while (temp != null) {
if(temp.id == node.id) {
//Match to Node, Replace Node
temp.front.next = node;
node.next = temp.next;
flag = true;
}
temp = temp.next;
}
if(!flag) {
System.out.println("No change information matched");
}
}
/**
* Delete Node
* @param node Node to delete
*/
public void deleteNode(PersonNode node) {
if(isEmpty()){
System.out.println("Chain list is empty");
return;
}
PersonNode temp = head.next;
//Check to see if deletion was successful
boolean flag = false;
while(temp != null) {
if(temp.id == node.id) {
temp.front.next = temp.next;
temp.next = null;
flag = true;
}
temp = temp.next;
}
if(!flag) {
System.out.println("The node was not found");
}
}
}
class PersonNode {
int id;
String name;
//Point to Next Node
PersonNode next;
//Point to the previous node
PersonNode front;
public PersonNode(int id, String name) {
this.id = id;
this.name = name;
}
@Override
public String toString() {
return "PersonNode{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
}
Run result:
Traversing a list of chains
PersonNode{id=1, name='Nyima'}
PersonNode{id=2, name='Lulu'}
Modify Node Information
Traversing a list of chains
PersonNode{id=1, name='Nyima'}
PersonNode{id=2, name='Wenwen'}
Delete Node
Traversing a list of chains
PersonNode{id=2, name='Wenwen'}
Process finished with exit code 0
3. Circular Chain List
Circular Chain List
The end node of a single-chain list points to the first node to form a circular chain table
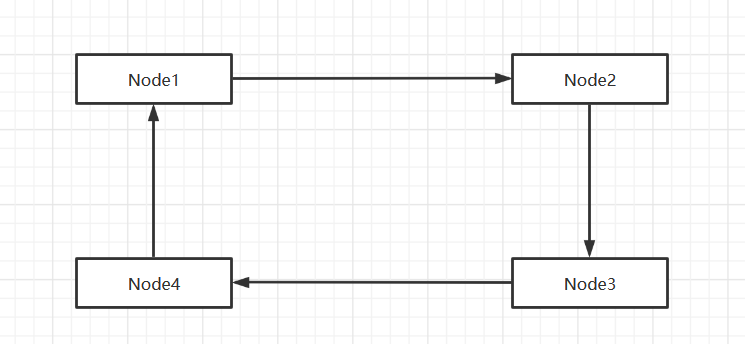
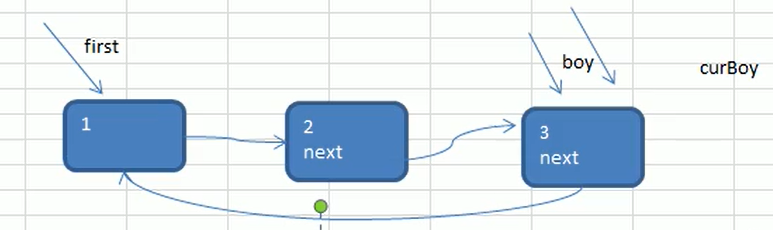
Traversing Ring Chain List
- Let a secondary pointer (variable) curBoy point to the first node first
- Then curBoy is created by traversing the ring list through a while loop. Next = first end
joseph
N people in a circle, counting from the first S, the first M will be killed, the last one will be killed, the rest will be killed to find out the sequence of killings
- For example, N=6, M=5, S=1, the order of killings is 6, 4, 5, 2, 1, 3
Rough ideas
- Traverse the list to find the node at the specified location
- Save the previous node of the specified node with a front for easy deletion
- When count==time, delete the node being traversed at this time, place it in the array, and initialize the value of count
- Several people have been circled with a variable loopTime, which is the last node when it equals length, put it directly into the array and return the number
Code:
public class yuesefuhuan {
public static void main(String[] args) {
CircleSingleLinkedList circleSingleLinkedList = new CircleSingleLinkedList();
circleSingleLinkedList.addBoy(5);
circleSingleLinkedList.showBoy();
//A child's circle indicates that five children were initially in the circle when counting 2 from the first child
circleSingleLinkedList.countBoy(1, 2, 5);
}
}
//Create a one-way chain table with a ring shape
class CircleSingleLinkedList {
//Create a first node with no current number
private Boy first = null;
//Add a child node to build a circular chain table
public void addBoy(int nums) {
//nums does a data check
if (nums < 1) {
System.out.println("nums Incorrect value for");
}
Boy curBoy = null;//Auxiliary pointer to help build a ring list
//Create our ring list with for
for (int i = 1; i<=nums; i++) {
//Create a child node based on number
Boy boy = new Boy(i);
//If it's the first child
if (i == 1) {
first = boy;
first.setNext(first);//Composition Ring
curBoy = first;//Point curBoy at the first child
} else {
curBoy.setNext(boy);
boy.setNext(first);
curBoy = boy;
}
}
}
//Traverse the current ring list
public void showBoy() {
//Determine if the list is empty
if (first == null) {
System.out.println("No children~~~");
return;
}
//Because first cannot move, we still use an auxiliary pointer to complete the traversal
Boy curBoy = this.first;
while (true) {
System.out.printf("Number of child %d \n", curBoy.getNo());
if (curBoy.getNext() == first) {//Description has been traversed
break;
}
curBoy = curBoy.getNext();//curBoy Move Back
}
}
/**
* Calculate the order in which children go out of circles based on user input
* @param startNo Indicates the number from which child to begin
* @param countNum Represent Count
* @param nums Indicates how many children were initially in the circle
*/
public void countBoy(int startNo, int countNum, int nums) {
//Validate data first
if (first == null || startNo < 1 || startNo > nums) {
System.out.println("Error in parameter input,Please re-enter");
return;
}
//Because first cannot move, we still use an auxiliary pointer to complete the traversal
Boy helper = this.first;
while (true) {
if (helper.getNext() == first) {//Description has been traversed
break;
}
helper = helper.getNext();//curBoy Move Back
}
//Let first and helper move k-1 times before your child counts
for (int j = 0; j < startNo - 1; j++) {
first = first.getNext();
helper = helper.getNext();
}
//When the child counts, let first and helper move m-1 times and then go out of circle
//This is a looping operation, knowing that there is only one node in the loop
while (true) {
if (helper == first) {//There is only one node in the circle
break;
}
//Let the first and helper pointers move countNum times at the same time
for (int j = 0; j < countNum - 1; j++) {
first = first.getNext();
helper = helper.getNext();
}
System.out.printf("Child %d Out of Circle\n", first.getNo());
first = first.getNext();
helper.setNext(first);
}
System.out.printf("The last remaining child number in the circle %d \n", first.getNo());
}
}
//Create a Boy class representing a node
class Boy {
private int no;//number
private Boy next;//Point to next node, default null
public Boy(int no) {
this.no = no;
}
public Boy(int no, Boy next) {
this.no = no;
this.next = next;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public Boy getNext() {
return next;
}
public void setNext(Boy next) {
this.next = next;
}
}
Output results:
Child Number 1 Child Number 2 Child Number 3 Child Number 4 Child Number 5 Kid 2 Out Circle Kid 4 Out Circle Kid 1 Out Circle Child 5 Out Circle Last remaining in circle No. 3 Process finished with exit code 0
3. Stack
1. Definition
- Stack is an ordered list of first-in-first-out items
- A stack is a special linear table that limits the insertion and deletion of elements in a linear table to only occur at the same end of the linear table. One end that allows insertion and deletion is called the top of the stack and the other end is called the bottom of the stack.
- The first element placed is at the bottom of the stack, and the last one is out. The last element put is at the top of the stack and comes out first
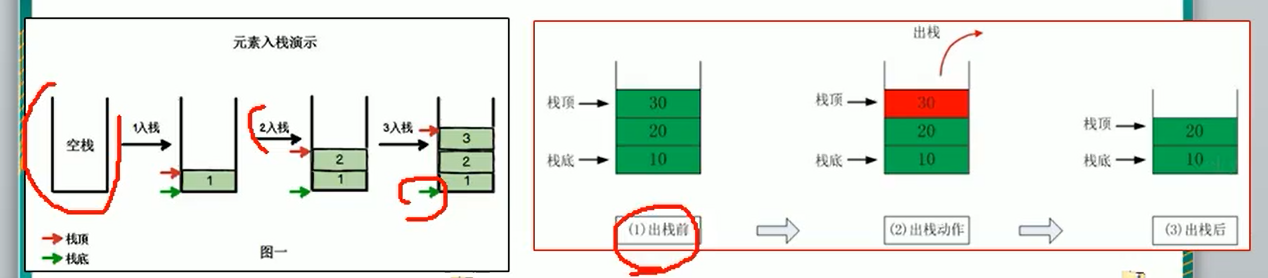
2. Scenarios
- Subprogram recursive call. Such as virtual machine stack in JVM
- Expression Conversion (Infix to Suffix) and Evaluation
- Traversal of Binary Trees
- Depth-first traversal of Graphs
3. Realization
Implemented with arrays
thinking
- Define top to represent top of stack, initial value is -1
- For stacking operations, let top++, then put the array stack[top] = data;
- Out of stack operation, first take out the element int value = stack[top], then let top--
- When top == -1, the stack is empty
- When top == maxSize-1, the stack is full
Code:
public class zhan {
public static void main(String[] args) {
ArrayStack stack = new ArrayStack(5);
//Stack
stack.push(1);
stack.push(2);
stack.push(3);
stack.push(4);
stack.push(5);
//Stack Out
System.out.println(stack.pop());
stack.list();
}
}
class ArrayStack {
private final int maxSize;
int[] stack;
private int top;
public ArrayStack(int maxSize) {
this.maxSize = maxSize;
stack = new int [this.maxSize];
top = -1;
}
private boolean isEmpty() {
return top == -1;
}
private boolean isFull() {
return top == maxSize-1;
}
public void push(int i) {
if(isFull()) {
throw new StackOverflowError("Full stack");
}
//Stack
top++;
stack[top] = i;
}
public int pop() {
if(isEmpty()) {
throw new EmptyStackException();
}
int retNum = stack[top];
top--;
return retNum;
}
//Show the stack [traverse the stack], traversal requires data to be displayed from the top of the stack
public void list() {
if (isEmpty()) {
System.out.println("Stack empty,no data~~~");
return;
}
//Data needs to be displayed from the top of the stack
for (int i = top; i >= 0; i--) {
System.out.printf("stack[%d] = %d \n", i, stack[i]);
}
}
}
Run result:
5 stack[3] = 4 stack[2] = 3 stack[1] = 2 stack[0] = 1 Process finished with exit code 0
4. Application
Expression evaluation
thinking
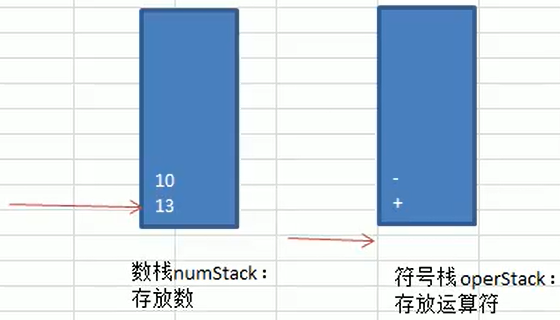
- Prepare an index index to help us iterate through expressions
- If the element at the index position is a number, it goes directly to the stack
- If the element at the index position is a symbol
- If the symbol stack is empty, go directly to the stack
- If the symbol stack is not empty
- If the precedence of a symbol at the index position is less than or equal to that of a symbol at the top of the stack, then one of the elements in the two stacks and one of the symbols in the stack will pop up and be calculated. Put the result of the operation on the stack and the symbol at the index position on the stack
- If the symbol at the index position takes precedence over the symbol at the top of the symbol stack, the symbol is pushed into the symbol stack
- When the expression is traversed, two numbers in the pop-up stack and one symbol in the symbol stack are computed, and the result is stacked
- There is only one value in the final stack, which is the result of the operation
- Be careful:
- Reads characters, so you need to subtract 0 from the ASCII code before saving the number
- If the number is a multi-digit number, you need to read it all the time until the next digit is not a number, then stitch the characters you read and press them together on the stack
Code:
public class Calculator {
public static void main(String[] args) {
String expression = "2+30*6-2";
//Create two stack numbers and symbol stacks
ArrayStack2 numStack = new ArrayStack2(10);
ArrayStack2 operStack = new ArrayStack2(10);
//Index, used to read elements in a string
int index = 0;
//Save read numbers and symbols
int num1 = 0;
int num2 = 0;
int oper = 0;
int res = 0;
int ch = ' ';//Save char s from each scan to ch
String keepNum = "";//For splicing multiple digits
//Start cycle scan expression
while (true) {
//Get every character in expression at once
ch = expression.substring(index, index + 1).charAt(0);
//Decide what ch is and process it accordingly
if (operStack.isOper((char) ch)) {//If it is an operator
//Determine if the current symbol stack is empty
if (!operStack.isEmpty()) {
//If there are operators in the symbol stack, then compare. If the priority of the current operator is less than or equal to the operator in the stack, you need to pop out two numbers from the stack.
//Then pop a symbol from the symbol stack, calculate it, put the result of the operation on the number stack, and put the current operator on the symbol stack
if (operStack.priority(ch) <= operStack.priority(operStack.peek())) {
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
res = numStack.cal(num1, num2, (char) oper);
//Put the result of an operation on the number stack
numStack.push(res);
//Then put the current operator on the symbol stack
operStack.push(ch);
} else {
//If the priority of the current operator is greater than that of the operator in the stack, it goes directly to the symbol stack
operStack.push(ch);
}
} else {
//If empty, go directly to the symbol stack
operStack.push(ch);
}
} else {
//If the number is directly on the stack
//numStack.push(ch - 48);
//Processing multi-digit
keepNum += ch-48;
//If ch is already the last expression, go directly to the stack
if (index == expression.length() - 1) {
numStack.push(Integer.parseInt(keepNum));
} else {
//Determine whether the next character is a number, the number continues to scan, the operator stacks
if (operStack.isOper(expression.substring(index + 1, index + 2).charAt(0))) {
//If the latter bit is an operator, keep Num = 1 or 123 on the stack
numStack.push(Integer.parseInt(keepNum));
//Keep Num empty
keepNum = "";
}
}
}
//Let index+1, and determine whether to scan to the end of expression
index++;
if (index >= expression.length()) {
break;
}
}
//When the expression is scanned, the corresponding numbers and symbols are pop ped out of the stack and run sequentially
while (true) {
//If the symbol stack is empty, the final result is calculated, with only one numeric result in the stack
if (operStack.isEmpty()) {
break;
}
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
res = numStack.cal(num1, num2, (char) oper);
numStack.push(res);//Push
}
//Popping the last number of stacks is the result
int res2 = numStack.pop();
System.out.println("Expression:"+expression +"="+res2);
}
}
//Create a stack first
class ArrayStack2 {
private final int maxSize;
int[] stack;
private int top;
public ArrayStack2(int maxSize) {
this.maxSize = maxSize;
stack = new int [this.maxSize];
top = -1;
}
//Returns the value at the top of the current stack
public int peek() {
return stack[top];
}
public boolean isEmpty() {
return top == -1;
}
public boolean isFull() {
return top == maxSize-1;
}
public void push(int i) {
if(isFull()) {
throw new StackOverflowError("Full stack");
}
//Stack
top++;
stack[top] = i;
}
public int pop() {
if(isEmpty()) {
throw new EmptyStackException();
}
int retNum = stack[top];
top--;
return retNum;
}
//Show the stack [traverse the stack], traversal requires data to be displayed from the top of the stack
public void list() {
if (isEmpty()) {
System.out.println("Stack empty,no data~~~");
return;
}
//Data needs to be displayed from the top of the stack
for (int i = top; i >= 0; i--) {
System.out.printf("stack[%d] = %d \n", i, stack[i]);
}
}
//Returns the priority of the operator, which is determined by the programmer, and is represented by a number
//The larger the number, the higher the priority
public int priority(int oper) {
if (oper == '*' || oper == '/') {
return 1;
} else if (oper == '+' || oper == '-') {
return 0;
} else {
return -1;//Assume that the current operator is only +-*/
}
}
//Determine if it is an operator
public boolean isOper(char val) {
return val == '+' || val == '-' || val == '*' || val == '/';
}
//computing method
public int cal (int num1, int num2, char oper) {
int res = 0;//res is used to store the results of the calculation
switch (oper) {
case '+':
res = num1 + num2;
break;
case '-':
res = num2 - num1;
break;
case '*':
res = num1 * num2;
break;
case '/':
res = num2 / num1;
break;
default:
break;
}
return res;
}
}
Run result:
Expression:2+30*6-2=180
5. Infix to Suffix
Suffix expression operation method
- Read expression from left to right
- Push into stack when numbers are encountered
- The top and second top elements of the stack pop up when an operator is encountered. Use the top element of the second-top element operator stack, and push the result of the operation into the stack until the stack is empty, and the result is the result of the operation
Design
Infix expression to suffix expression
-
Read the infix expression from left to right and create stacks and queues q
-
If you read the number of the element, it will be queued directly into q
-
If you read
operator
(Operator Decision)
- If s is empty, press the operator into S
- If s is not empty
- If the operator is left parenthesis, press s directly
- If the operator is a right bracket, the elements in s are sequentially stacked and queued to Q until the left bracket is encountered (brackets are not placed in q)
- If the operator takes precedence over the operator at the top of the s stack, press the element into S
- If the precedence of this operator is less than or equal to the operator at the top of the s stack, the element at the top of the s stack pops up and places it in q, which redefines the stacking operation (operator decision step)
-
If the infix expression has been read, then the elements in s are put out of the stack in q
-
The elements in q queue in turn, which is the suffix expression
Code:
public class PolandNotation {
public static void main(String[] args) {
//Completes the function of converting a suffix expression to a suffix expression
//1+((2+3)*4)-5 ==> 1 2 3 + 4 * + 5 -
//1.Place 1+((2+3)*4) -5 in the ArrayList [1, +, (, (, (, 2, +, 3,), *, 4,)-, 5] of the list.
//2. Infix Trans Suffix ArrayList [1, +, (, (, 2, +, 3,), *, 4,), -, 5] => ArrayList [1, 2, 3, +, 4, *, +, 5,-]
String expression = "1+((2+3)*4)-5";
List<String> infixExpressionList = toInfixExpressionList(expression);
System.out.println("Corresponding to infix expression list:"+infixExpressionList);
List<String> suffixExpressionList = parseSuffixExpressionList(infixExpressionList);
System.out.println("Corresponding to the suffix expression list:"+suffixExpressionList);
System.out.println("Calculation results:"+calculate(suffixExpressionList));
//Define an inverse Polish expression first
//(3+4)*5-6 => 3 4 + 5 * 6 - =>29
String suffixExpression = "3 4 + 5 * 6 - ";
//thinking
//1. Put "3 4 + 5 * 6 -" in the ArrayList first
//2. Pass the ArrayList to a method that traverses the ArrayList with the stack to complete the calculation
List<String> list = getListString(suffixExpression);
System.out.println("rpnList="+list);
int res = calculate(list);
System.out.println("The result of the calculation is:"+res);
}
//Convert infix expression to corresponding list
public static List<String> toInfixExpressionList(String s) {
//Define what the list holds for the infix expression
ArrayList<String> list = new ArrayList<>();
int i = 0;//This is a pointer that traverses the infix expression string
String str;//Corresponding multidigit stitching
char c;//Place in c every character traversed
do {
//If c is a non-number you need to access the list
if ((c = s.charAt(i)) < 48 || (c = s.charAt(i)) > 57) {
list.add("" + c);
i++;
} else {//Consider multiple digits if it is a number
str = "";//Set str to ""'0'[48]->'9'[57]
while (i < s.length() && (c = s.charAt(i)) >= 48 && (c = s.charAt(i)) <= 57) {
str += c;//Stitching
i++;
}
list.add(str);
}
} while (i < s.length());
return list;
}
//Infix Trans Suffix ArrayList [1,+, (, (, (, 2, +, 3,), *, 4,), -, 5] => ArrayList [1, 2, 3, +, 4, *, +, 5,-]
public static List<String> parseSuffixExpressionList(List<String> ls) {
//Define two stacks
Stack<String> s1 = new Stack<>();
//The s2 stack is stored directly in a queue because it does not have a pop operation and needs to be output in reverse order later
ArrayList<String> s2 = new ArrayList<>();
//ergodic
for (String item : ls) {
//Add s2 if it is a number
if (item.matches("\\d+")) {
s2.add(item);
} else if (item.equals("(")) {
s1.push(item);
} else if (item.equals(")")) {
//If')', pop up the operator at the top of the s1 stack one by one and press s2 until'('is encountered, discarding the pair of parentheses
while (!s1.peek().equals("(")) {
s2.add(s1.pop());
}
s1.pop();//Pop'('out of s1 stack
} else {
//When the priority of item is less than or equal to the s1 stack top operator, pop up the s1 stack top operator and add it to s2, then compare it with the new stack top operator in s1
while (s1.size() != 0 && Operation.getValue(s1.peek()) >= Operation.getValue(item)) {
s2.add(s1.pop());
}
//You also need to push item s onto the stack
s1.push(item);
}
}
//Pop up the remaining operators in s1 and add s2
while (s1.size() != 0) {
s2.add(s1.pop());
}
return s2;//Since it is stored in a list, the sequential output is the list of the corresponding suffix expression
}
//Put an inverse Polish expression, data and operators into the ArrayList in turn
public static List<String> getListString(String suffixExpression) {
//Split suffixExpression
String[] split = suffixExpression.split(" ");
List<String> list = new ArrayList<>();
for (String s : split) {
list.add(s);
}
return list;
}
//Complete the operation of the inverse Polish expression
/**
* 1.Scan left to right to push 3 and 4 onto the stack
* 2.Encountered the + operator, so pop up 4 and 3 (4 is the top element, 3 is the second top element), calculate the value of 3+4, get 7, and put 7 on the stack
* 3.Put 5 on the stack
* 4.Next comes the X operator, so pop up 5 and 7, calculate that 7x 5 equals 35, and put 35 on the stack
* 5.Put 6 on the stack;
* 6.The final result is the -operator, which calculates the value of 35-6, or 29.
* @return
*/
public static int calculate(List<String> ls) {
Stack<String> stack = new Stack<>();
//Traversing ls
for (String item : ls) {
//Number of regular expression fetches
if (item.matches("\\d+")) {//The match is a multidigit stack
stack.push(item);
} else {
//pop out two numbers and run them on the stack
int num2 = Integer.parseInt(stack.pop());
int num1 = Integer.parseInt(stack.pop());
int res = 0;
if (item.equals("+")) {
res = num1 + num2;
} else if (item.equals("-")) {
res = num1 - num2;
} else if (item.equals("*")) {
res = num1 * num2;
} else if (item.equals("/")) {
res = num1 / num2;
} else {
throw new RuntimeException("Error in operator");
}
//Put res on the stack
stack.push("" + res);
}
}
//The last data left in the stack is the result of the operation
return Integer.parseInt(stack.pop());
}
}
//Writing an Operation returns the priority corresponding to an operator
class Operation {
private static int ADD = 1;
private static int SUB = 1;
private static int MUL = 2;
private static int DIV = 2;
public static int getValue(String operation) {
int result = 0;
switch (operation) {
case "+":
result = ADD;
break;
case "-":
result = SUB;
break;
case "*":
result = MUL;
break;
case "/":
result = DIV;
break;
default:
System.out.println("The operator does not exist");
break;
}
return result;
}
}
Run result:
Corresponding to infix expression list:[1, +, (, (, 2, +, 3, ), *, 4, ), -, 5] The operator does not exist The operator does not exist Corresponding to the suffix expression list:[1, 2, 3, +, 4, *, +, 5, -] Calculation results:16 rpnList=[3, 4, +, 5, *, 6, -] The result of the calculation is:29 Process finished with exit code 0
4. Recursion
1. Concepts
Recursion is when a method calls itself, passing in different variables each time it calls. Recursion helps programmers solve complex problems while keeping code simple. And recursively used the virtual machine stack
2. Solvable Issues
mathematical problem
- Queens of Eight
- Hanoi
- Find factorial
- Labyrinth problem
- Balls and Baskets
Various sorting algorithms
3. Rules
- When a method is executed, a new protected stand-alone space (stack space) is created
- Method variables are independent and do not interact
- If a reference type variable (such as an array) is used in a method, the data of that reference type is shared
- Recursion must approximate the condition under which it exits or it is infinite recursion with StackOverflowError
- When a method finishes executing, or encounters a return, it returns, who calls it, to whom the result is returned, and when the method finishes executing or returns, the method finishes executing
4. Labyrinth problems
thinking
- Represent a map with a two-dimensional matrix
- 1 represents the boundary
- 0 means the site has not been done
- 2 stands for walk and walk
- 3 Represents walk but cannot walk
- Set the starting and ending points and the walking strategy for each location
- Walking strategy refers to the order in which direction you are going at that point, as follows - > Right - > Up - > Left (invokes the method of finding a path, using recursion)
- Assume that the point can be reached each time you walk, and then judge by strategy. If all the strategies cannot be reached, the point cannot be reached.
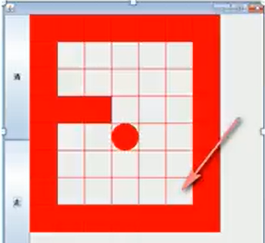
graphic
Initial Map
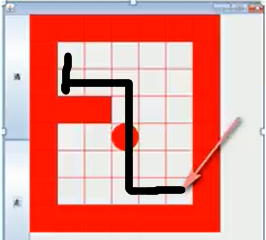
Walking Path
Strategy: bottom right top left
Code:
public class migong {
public static void main(String[] args) {
//Get a map
int length = 8;
int width = 7;
int[][] map = getMap(length, width);
//Set some barriers
map[3][1] = 1;
map[3][2] = 1;
//Print Map
System.out.println("The map is as follows");
for(int i=0; i<length; i++) {
for(int j=0; j<width; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}
//Use recursive backtracking to find a way to the ball
getWay(map,1,1);
//Output New Map Ball Passed and Identified Recursions
System.out.println("Ball Passes,Map situation identified:");
for(int i=0; i<length; i++) {
for(int j=0; j<width; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}
}
/**
* Create a map
* @param length The length of the map
* @param width Width of the map
* @return Created Maps
*/
public static int[][] getMap(int length, int width) {
int[][] map = new int[length][width];
//First set the first and last lines to 1 (boundary)
for(int i=0; i<width; i++) {
map[0][i] = 1;
map[length-1][i] = 1;
}
//Set the first and last columns to 1
for(int i=0; i<length; i++) {
map[i][0] = 1;
map[i][width-1] = 1;
}
return map;
}
/**
* 1.map Represent a map
* 2.i j Indicates where to start from on the map (1,1)
* 3.If the globule reaches the map[6][5], the path is found
* 4.Conventions: When map[i][j] is 0, the point has not been traversed and 1 represents a wall; 2 indicates that the pathway is accessible; 3 indicates that the point has already passed but cannot be reached
* 5.When walking a labyrinth, you need to determine a strategy (method) under - > right - > up - > left, if that point is not accessible then go back
* @param map Represent a map
* @param i Where to start
* @param j
* @return Return true if a path is found, false otherwise
*/
public static boolean getWay(int[][] map, int i, int j) {
if (map[6][5] == 2) {//Pathway has found OK
return true;
} else {
if (map[i][j] == 0) {//If the current point has not yet passed
//Follow strategy - > Right - > Up - > Left
map[i][j] = 2;//Assuming this point is accessible
if (getWay(map, i+1, j)) {
return true;
} else if (getWay(map, i, j+1)) {
return true;
} else if (getWay(map, i-1, j)) {
return true;
} else if (getWay(map, i, j-1)) {
return true;
} else {
//Explain that this point is dead end
map[i][j] = 3;
return false;
}
} else { //If map[i][j]!= 0, maybe 12 3
return false;
}
}
}
}
Output:
The map is as follows 1 1 1 1 1 1 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 1 1 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 Ball Passes,Map situation identified: 1 1 1 1 1 1 1 1 2 0 0 0 0 1 1 2 2 2 0 0 1 1 1 1 2 0 0 1 1 0 0 2 0 0 1 1 0 0 2 0 0 1 1 0 0 2 2 2 1 1 1 1 1 1 1 1 Process finished with exit code 0
5. Queens of Eight
The Eight Queens problem, an old and well-known problem, is a typical case of backtracking algorithms. The question was posed by chess player Max Bessel in 1848: × Eight queens are placed on an eight-grid chess board so that they cannot attack each other, that is, no two Queens can be in the same row, column or slash. Ask how many swings (92) there are.
thinking
- Place the first queen in the first row and column
- Place the second queen in the second row, in the first column, to determine if it will attack each other, and if it will, put it in the second, third, and fourth columns until it will not attack each other.
- Place the third queen in the first column of the third row to determine if it will attack each other, and if it will, put it in the second, third, fourth columns.. until it will not attack each other, and so on. During the placement process, it may change the position of the queen in front of it.
- When you get the correct solution, you go back to the previous row to find all the solutions for the first queen in the first row and column
- Place the first queen in the first row, in the second column, and repeat the four steps above
- Be careful:
- The board itself should be represented by a two-dimensional array, but since the queen is in a fixed number of rows, it can be simplified to a one-dimensional array. arr[8] = {0,4,7,5,2,4,1,3}// The corresponding arr subscript represents the row, that is, the queen, arr[i] = val, Val represents the i+1 queen, and is placed in column val+1 of line i+1
- Array subscripts represent the number of rows the Queen is in, so when deciding whether or not to be on the same row-column slash, you just need to decide whether or not to be on the same column and slash.
- Determine if the values are the same
- Is the same slash: line number - line number equal to column number - column number, and column number subtracted to take absolute value
Code:
public class Queue8 {
//Define a max to show how many queens there are
int max = 8;
//Define the array array to hold the result of the queen's placement, for example: arr[8] = {0,4,7,5,2,4,1,3}
int[] array = new int[max];
static int count = 0;
public static void main(String[] args) {
Queue8 queue8 = new Queue8();
queue8.check(0);
System.out.println("Altogether"+count+"species");
}
//Write a method to place the n th Queen
//It is important to note that check has for (int I = 0; I < max; i++) in the check every time it is recursive, so there is a backtrace
private void check(int n) {
if (n == max) {//n=8 is eight queens ready
print();
return;
}
//Place Queen in turn and decide if there is a conflict
for (int i = 0;i < max; i++) {
//Judge the current queen n and place it in the first column of the row
array[n] = i;
//Determine if there is a conflict when placing the nth queen i n column I
if (judge(n)) {//No conflict
//Then put n+1 queens, and recursion begins
check(n+1);
}
}
//If there is a conflict, continue executing array[n] = i, i.e., place the nth queen at a position that moves back on this line
}
/**
* Check to see if the queen conflicts with the queen already placed in front when we place the nth queen
* @param n
* @return
*/
private boolean judge(int n) {
for (int i = 0; i < n; i++) {
//1.array[i] == array[n] to determine if the nth queen is i n the same column as the previous ith queen
//2.Math.abs(n-1) == Math.abs(array[n] - array[i]) determines if the nth queen is on the same slash as the previous ith queen
//n = 1 Place column 2 1 n = 1 array[1] = 1
//Math.abs(1-0) == 1 Math.abs(array[n] - array[i]) = Math.abs(1 - 0) = 1
//3. Judging that it is not necessary to be on the same line, n is increasing each time
if (array[i] == array[n] || Math.abs(n-i) == Math.abs(array[n] - array[i])) {
return false;
}
}
return true;
}
//Queen position output
private void print() {
count++;
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}
}
5. Sorting
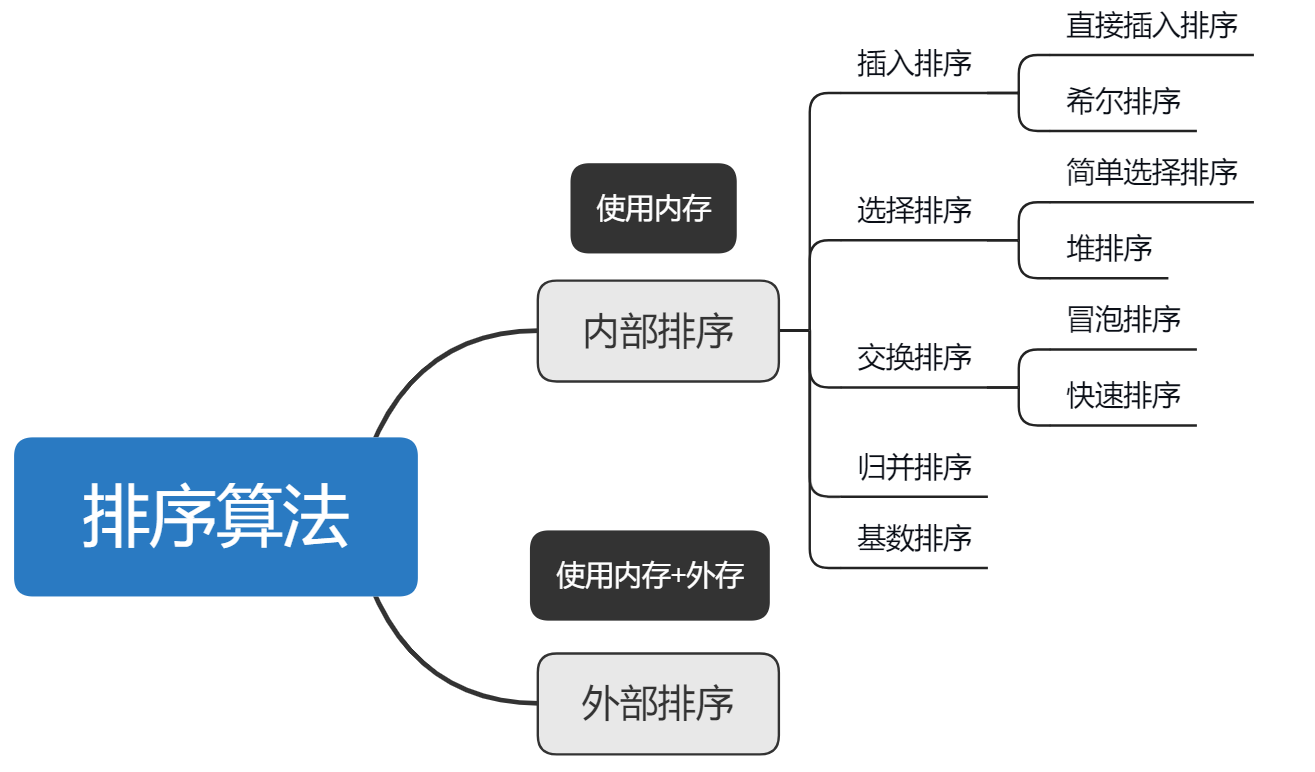
1. Common sorting algorithms
- Internal sorting: All data that needs to be processed is loaded into internal memory (memory) for sorting
- External sorting: cannot be fully loaded into memory and needs to be sorted by external storage (files, etc.)
2. Time complexity of the algorithm
Time Frequency and Time Complexity
Time Frequency T(n)
The time it takes an algorithm to execute is theoretically impossible to calculate and must be run on a computer to know. However, it is impossible and unnecessary to test each algorithm on the computer. Just know which algorithm takes more time and which one takes less time. Moreover, the time spent in an algorithm is proportional to the number of executions of the statements in the algorithm, which algorithm takes more time to execute the statements. The number of statement executions in an algorithm is called the frequency of statements or the frequency of time. It is recorded as T(n).
Time Complexity O(n)
In general, the number of times the basic operation is repeated in the algorithm is a function of the scale of the problem n, expressed as T(n). If there is an auxiliary function f(n), so that when n approaches infinity, the limit value of T(n)/f(n) is not equal to a constant of zero, then f(n) is the same order function of T(n). T(n)=O(f(n)), O(f(n)) is the asymptotic time complexity of the algorithm, referred to as the time complexity for short.
At T(n)=4n ²- In 2n+2, there is f(n)=n ², If the limit value of T(n)/f(n) is 4, then O(f(n), or time complexity, is O(n) ²)
- Ignore coefficients of time frequency, low order constants for time complexity that is not constants only
- For time complexity with constants only, consider constants to be 1
Common time complexity
Constant Order O(1)
int i = 1; i++;Copy
No matter how many lines the code executes, the time complexity is O(1) as long as there is no complex structure such as loops
Logarithmic O(log2n)
while(i<n) {
i = i*2;
}Copy
Here I does not increase to n i n turn, but multiplies each time. Suppose I is greater than n after X cycles. Then 2x = n, x=log2n
Linear Order O(n)
for(int i = 0; i<n; i++) {
i++;
}Copy
Here, the code in the loop executes n+1 times with O(n) time complexity
Linear logarithmic order O(nlog2n)
for(int i = 0; i<n; i++) {
j = 1;
while(j<n) {
j = j*2;
}
}Copy
There is a loop outside here, n times. Internal is also a loop, but the time complexity of the internal f loop is log2n
So the overall time complexity is linear logarithmic O(nlog2n)
Square Order O(n2)
for(int i = 0; i<n; i++) {
for(int j = 0; j<n; j++) {
//Circulatory body
}
}Copy
Cubic O(n3)
for(int i = 0; i<n; i++) {
for(int j = 0; j<n; j++) {
for(int k = 0; k<n; k++) {
//Circulatory body
}
}
}Copy
It can be seen that the complexity of the square and cubic order is mainly determined by whether or not they cycle through several layers.
K-th order O(n^k)
Exponential order O(2^n)
The time complexity of common algorithms is in the order of O(1) < O(log2n) < O(n) < O(n log2n) < O(n^2) < O(n^3) < O(n^k) < O(2^n). As the problem size n increases, the time complexity above increases, and the algorithm execution efficiency decreases, exponential order algorithms should be avoided as much as possible.
3. Time complexity of sorting algorithm
| Sorting algorithm | average time | Worst Time | stability | Spatial Complexity | Remarks |
|---|---|---|---|---|---|
| Bubble sort | O(n2) | O(n2) | Stable | O(1) | n Smaller Hours |
| Exchange sort | O(n2) | O(n2) | Instable | O(1) | n Smaller Hours |
| Select Sort | O(n2) | O(n2) | Instable | O(1) | n Smaller Hours |
| Insert Sort | O(n2) | O(n2) | Stable | O(1) | Most of them are already in good order |
| Cardinality sorting | O(n*k) | O(n*k) | Stable | O(n) | Two-dimensional array (bucket), one-dimensional array (position of first element in bucket) |
| Shell Sort | O(nlogn) | O(ns)(1<s<2) | Instable | O(1) | s is the selected grouping |
| Quick Sort | O(nlogn) | O(n2) | Instable | O(logn) | n Greater Hours |
| Merge Sort | O(nlogn) | O(nlogn) | Stable | O(1) | n Greater Hours |
| Heap Sorting | O(nlogn) | O(nlogn) | Instable | O(1) | n Greater Hours |
4. Bubble Sorting
Algorithmic steps
- Compare adjacent elements. If the first one is bigger than the second, swap the two.
- Do the same work for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end. When this is done, the last element will be the maximum number.
- Repeat the above steps for all elements except the last one.
- Continue repeating the above steps for fewer and fewer elements each time until no pair of numbers need to be compared.
- There are a total number of array elements - 1 large cycle, and fewer and fewer elements to compare in each large cycle.
- Optimize: If no exchange occurs in a large cycle, the order is proven.
Code:
public class BubbleSort {
public static void main(String[] args) {
int arr[] = {3,9,-1,10,20};
//Bubble sort
int temp = 0;
boolean flag = false;//Identifies whether a variable has been swapped or not
for (int i = 1; i < arr.length; i++) {
for (int j = 0; j < arr.length - i; j++) {
if (arr[j] < arr[j+1]) {
flag = true;
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
System.out.println("No."+i+"After the trip is ordered:");
System.out.println(Arrays.toString(arr));
if (!flag) {
break;//No swap occurred in a single sort
} else {
flag = false;//Reset flag!!! Make the next judgment
}
}
}
}
Output results:
After the first sorting: [9, 3, 10, 20, -1] After the second sorting: [9, 10, 20, 3, -1] After the third sorting: [10, 20, 9, 3, -1] After the fourth sorting: [20, 10, 9, 3, -1] Process finished with exit code 0
5. Select Sort
Algorithmic steps
- Traverse the entire array, find the smallest (largest) element, and place it at the beginning of the array.
- Walk through the remaining arrays to find the smallest (large) element of the remaining elements and place it in the second position of the array.
- Repeat the above steps until the sorting is complete.
- The number of elements in the array needs to be traversed - once in all. When the second largest (smaller) element is found, it can be stopped. At this point, the last element must be the largest (smallest) element.
Code:
public class SelectSort {
public static void main(String[] args) {
int arr[] = {1,10,5,6,4,9,3};
//Select Sort
for (int i = 0; i < arr.length-1; i++) {
int minIndex = i;
int min = arr[i];
for (int j = i+1; j <arr.length; j++) {
if (min > arr[j]) {
min = arr[j];//Reset min
minIndex = j;//Reset minIndex
}
}
//Put the minimum value at arr[i]
if (minIndex != i) {
arr[minIndex] = arr[i];
arr[i] = min;
}
System.out.println("No."+(i+1)+"After the trip is ordered:");
System.out.println(Arrays.toString(arr));
}
}
}
Output:
After the first sorting: [1, 10, 5, 6, 4, 9, 3] After the second sorting: [1, 3, 5, 6, 4, 9, 10] After the third sorting: [1, 3, 4, 6, 5, 9, 10] After the fourth sorting: [1, 3, 4, 5, 6, 9, 10] After the fifth sorting: [1, 3, 4, 5, 6, 9, 10] After the sixth sorting: [1, 3, 4, 5, 6, 9, 10] Process finished with exit code 0
6. Insert Sort
Algorithmic steps
- Consider the first element of the sequence to be sorted as an ordered sequence, and the second to the last element as an unsorted sequence.
- Unordered sequences are scanned from beginning to end, and each element scanned is inserted into the appropriate position in the ordered sequence. (If the element to be inserted is equal to an element in an ordered sequence, the element to be inserted is inserted after the equal element.
Code:
public class InsertSort {
public static void main(String[] args) {
int arr[] = {344,101,119,1};
for (int i=1; i < arr.length; i++) {
//Define the number to insert
int insertVal = arr[i];
//Subscript of the number preceding arr[1]
int insertIndex = i-1;
//Find the insert location for insetVal
//1. Guarantee that insertIndex >= 0 guarantees insertVal to find insert locations that do not exceed bounds
//2.insertVal <arr[insertIndex] number to insert, insert location not found yet
//3. You need to move arr[insertIndex] back
while(insertIndex >= 0 && insertVal <arr[insertIndex]) {
arr[insertIndex+1] = arr[insertIndex];
insertIndex--;
}
//Exit the while loop, indicating insertIndex+1 was found at the insert location
if (insertIndex+1 != i) {
arr[insertIndex+1] = insertVal;
}
System.out.println("No."+i+"After the trip is ordered:");
System.out.println(Arrays.toString(arr));
}
}
}
Run result:
After the first sorting: [101, 344, 119, 1] After the second sorting: [101, 119, 344, 1] After the third sorting: [1, 101, 119, 344] Process finished with exit code 0
7. Hill Sorting
Review: Insert Sorting Problems
When the last element is the smallest element of the entire array, it can be time consuming to move each element in the preceding ordered array one bit backward.
So we have Hill sort to help us turn arrays from out of order to whole order and then into order.
Algorithmic steps
- Select an incremental sequence t1 (typically array length/2), t2 (typically a grouping length/2),..., tk, where ti > tj, TK = 1;
- Sort the sequences by K times according to the number of incremental series k;
- For each sorting, the columns to be sorted are divided into several m-length subsequences according to the corresponding incremental ti, and the subsequences are inserted and sorted directly. When the increment factor is only 1, the entire sequence is treated as a table, and the length of the table is the length of the entire sequence.
Sketch Map
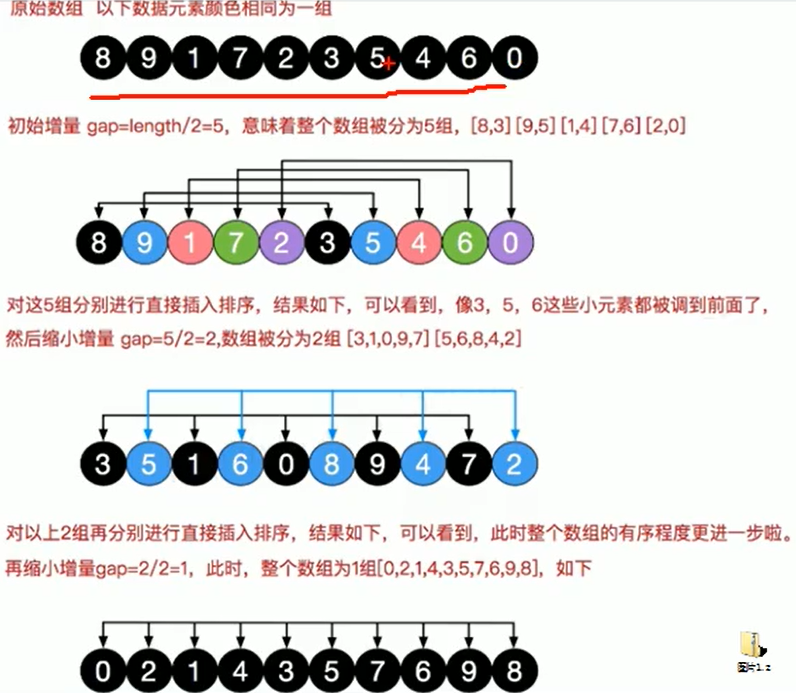
Code:
public static void main(String[] args) {
int arr[] = {1,10,5,6,4,9,3,22};
//Hill Sort Shift Method
//Increment gap s and gradually reduce increments
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
//Gradually insert and sort the group from the gap element
for (int i = gap; i < arr.length; i++) {
int j = i;
int temp = arr[j];
while (j - gap >= 0 && temp < arr[j - gap]) {
//move
arr[j] = arr[j - gap];
j -= gap;
}
if (j != i) {
arr[j] = temp;
}
}
System.out.println("After each sorting:");
System.out.println(Arrays.toString(arr));
}
}
}
Run result:
After each sorting: [1, 9, 3, 6, 4, 10, 5, 22] After each sorting: [1, 6, 3, 9, 4, 10, 5, 22] After each sorting: [1, 3, 4, 5, 6, 9, 10, 22] Process finished with exit code 0
8. Quick Sorting
Algorithmic steps
- Pick out an element from a number of columns, called a pivot;
- Reorder the number columns, all elements smaller than the base value are placed in front of the base, and all elements larger than the base value are placed behind the base (the same number can be on either side). After the partition exits, the benchmark is in the middle of the column. This is called a partition operation;
- Recursively sorts the subordinate columns of elements less than the base value and those greater than the base value.
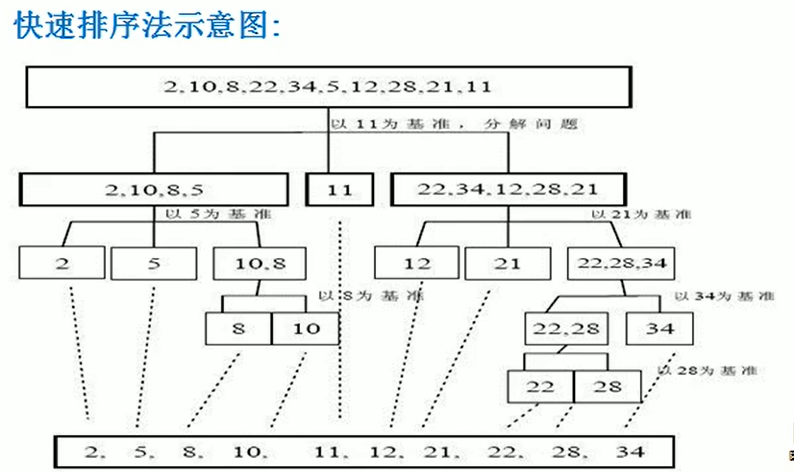

Code:
public class QuickSort {
public static void main(String[] args) {
int arr[] = {-9,78,0,23,-567,70};
quickSort(arr, 0, arr.length - 1);
System.out.println("arr:"+ Arrays.toString(arr));
}
public static void quickSort(int[] arr, int left, int right) {
int l = left;//Left Subscript
int r = right;//Right Subscript
//pivot median axis value
int pivot = arr[(left + right) / 2];
int temp = 0;
//The purpose of the while loop is to make the pivot value smaller than the pivot value to the left
//Place greater than pivot on the side
while (l < r) {
//Keep looking to the left of pivot, find a value greater than or equal to pivot before exiting
while (arr[l] < pivot) {
l += 1;
}
//Look all the way to the right of pivot, find a value less than or equal to pivot before exiting
while (arr[r] > pivot) {
r -= 1;
}
//If L >= r indicates that all values on the left side of pivot are less than or equal to pivot
//All values on the right side of pivot are greater than or equal to pivot
if (l >= r) {
break;
}
//exchange
temp = arr[l];
arr[l] = arr[r];
arr[r] = temp;
//Ar[l] == pivot, r--move forward after swapping
if (arr[l] == pivot) {
r -= 1;
}
//Ar[r] == pivot, l++ moved back after swapping
if (arr[r] == pivot) {
l += 1;
}
}
//if l==r must be l++ r--otherwise stack overflow occurs
if (l == r) {
l += 1;
r -= 1;
}
//Recursion Left
if (left < r) {
quickSort(arr, left, r);
}
if (right > l) {
quickSort(arr, l, right);
}
}
}
Output results:
arr:[-567, -9, 0, 23, 70, 78] Process finished with exit code 0
9. Merge Sort
Algorithmic steps
Merging and sorting uses the idea of dividing and governing, the difficult point is to govern
- Request space so that it is the sum of two sorted sequences that hold the merged sequence
- Sets two pointers, starting at the position of two sorted sequences
- Compare the elements that the two pointers point to, select the relatively small elements to put into the merge space, and move the pointer to the next location
- Repeat the last step until a pointer reaches the end of the sequence
- Copy all remaining elements of another sequence directly to the end of the merge sequence
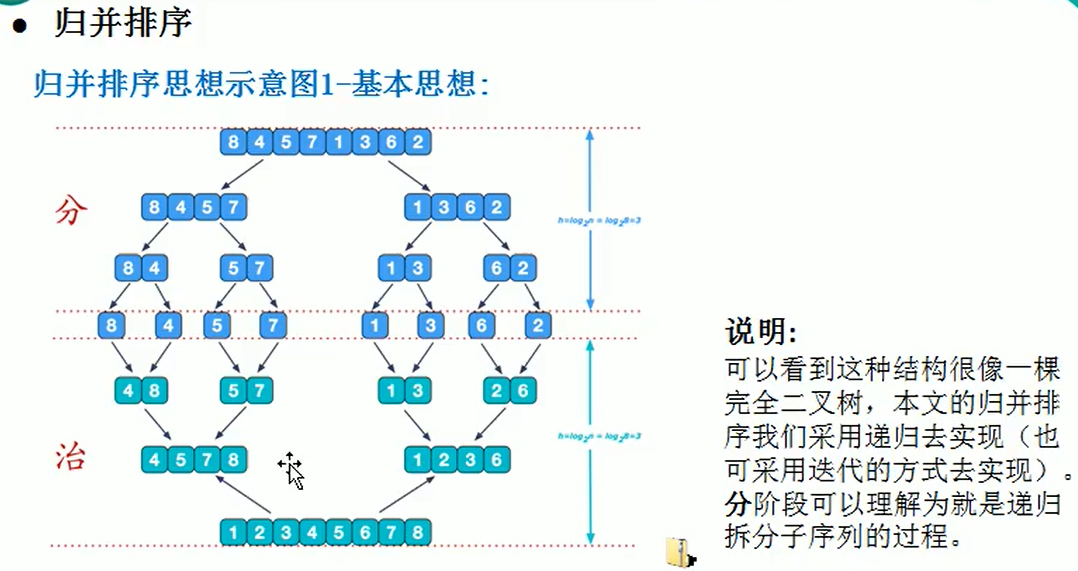
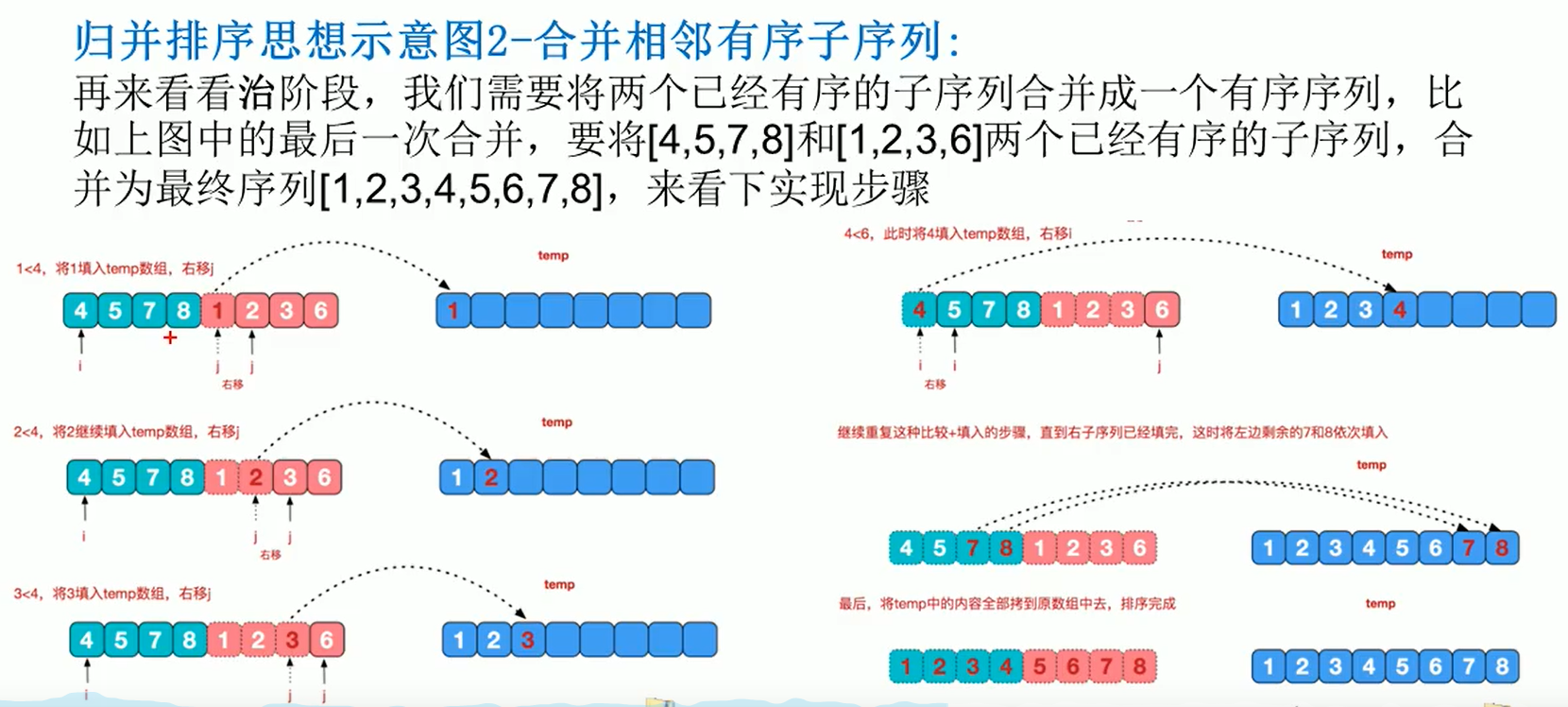
Code:
public class MergetSort {
public static void main(String[] args) {
int arr[] = {8,4,5,7,1,3,6,2};
int temp[] = new int[arr.length];
mergeSort(arr, 0, arr.length - 1, temp);
System.out.println("After merging and sorting:"+ Arrays.toString(arr));
}
//Score+Method
public static void mergeSort(int[] arr, int left, int right, int[] temp) {
if (left < right) {
int mid = (left + right) / 2;//Intermediate Index
//Decomposition recursively to the left
mergeSort(arr, left, mid, temp);
//Decomposition Recursively Right
mergeSort(arr, mid + 1, right, temp);
//To merge
merge(arr, left, mid, right, temp);
}
}
/**
* Method of merging
* @param arr Sorted original number
* @param left Initial index of left ordered sequence
* @param mid Intermediate Index
* @param right Right Index
* @param temp Array to be transferred
*/
public static void merge(int arr[], int left, int mid, int right, int[] temp) {
int i = left;//Initialize the initial index of the left ordered sequence of i
int j = mid + 1;//Initialize initial index of j right ordered sequence
int t = 0;//Current index to temp array
//(1)
//Fill the left and right (ordered) data into the temp array as a rule first
//Until one side of the ordered sequence is processed
while (i <= mid && j <=right) {
//If the current element of the ordered sequence on the left is less than or equal to the current element of the ordered sequence on the right
//Fill the current element on the left with the temp array and t++ i++.
if (arr[i] < arr[j]) {
temp[t] = arr[i];
t += 1;
i += 1;
} else {//Conversely, populate the current element of the ordered sequence on the right into the temp array
temp[t] = arr[j];
t += 1;
j += 1;
}
}
//(2)
//Fill one side of data with remaining data into temp at a time
while (i <= mid) {//The ordered sequence on the left has the remaining elements, so it's all populated with temp
temp[t] = arr[i];
t += 1;
i += 1;
}
while (j <= right) {//The ordered sequence on the right has the remaining elements, so it's all populated with temp
temp[t] = arr[j];
t += 1;
j += 1;
}
//(3)
//Copy elements of temp array to arr
//Note that not all copies are made every time
t = 0;
int tempLeft = left;
while (tempLeft <= right) {
arr[tempLeft] = temp[t];
t += 1;
tempLeft += 1;
}
}
}
Run result:
After merging and sorting:[1, 2, 3, 4, 5, 6, 7, 8] Process finished with exit code 0
10. Cardinal Sorting
Algorithmic steps
- Unify all values (positive integers) to be compared to the same number of digits, with the shorter digits preceded by zeros
- Sort one by one starting at the lowest bit
- After sorting from the lowest to the highest (bits->10->100->...->the highest), the sequence becomes an ordered sequence.
- We need to get the maximum number of digits
- You can find the length of the maximum number by changing it to String type
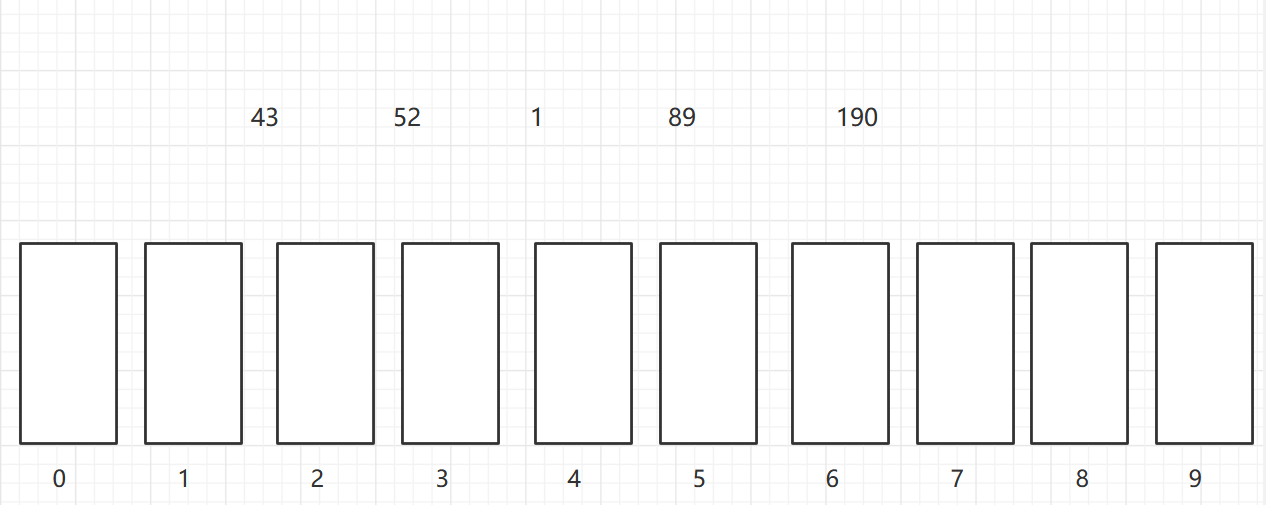
Place in the corresponding bucket in bits
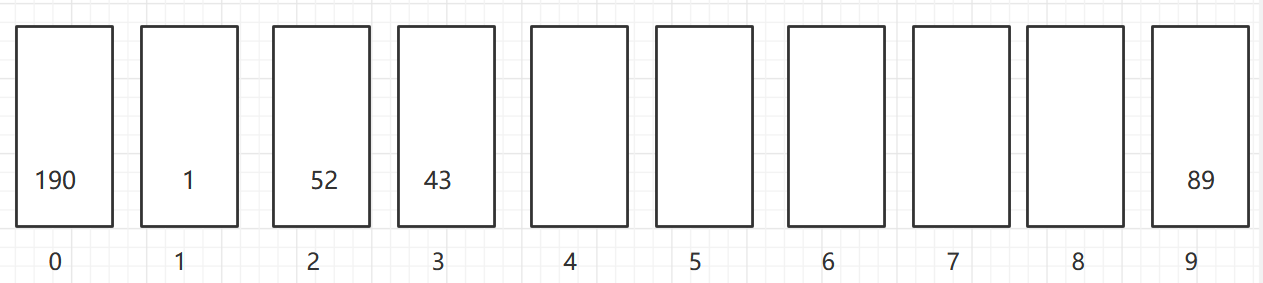
Take out one by one, if there are many elements in the same bucket, put in first take out first
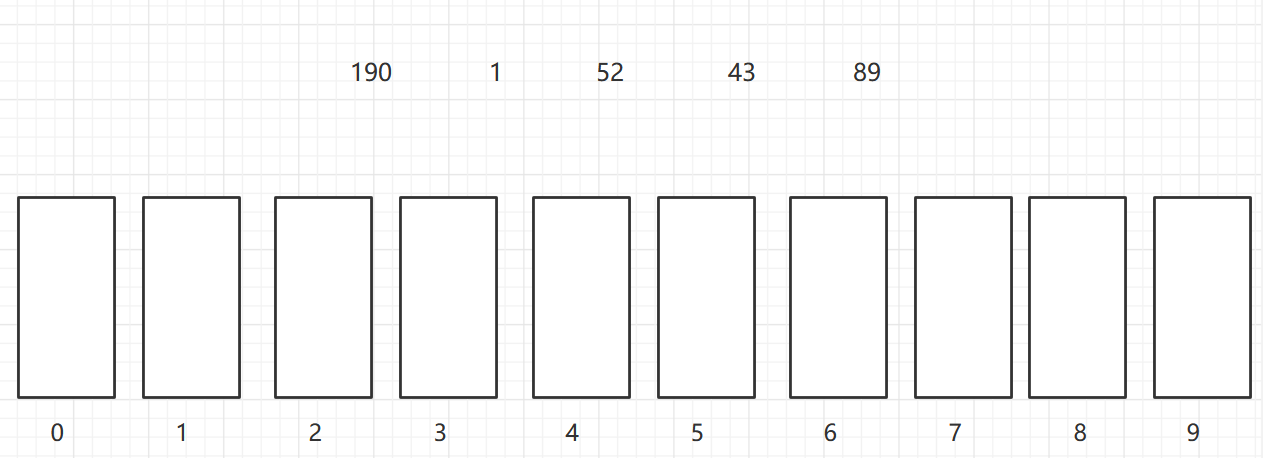
Then place the 10 digits in the corresponding bucket, and fill the 0 digits in front of the 10 digits
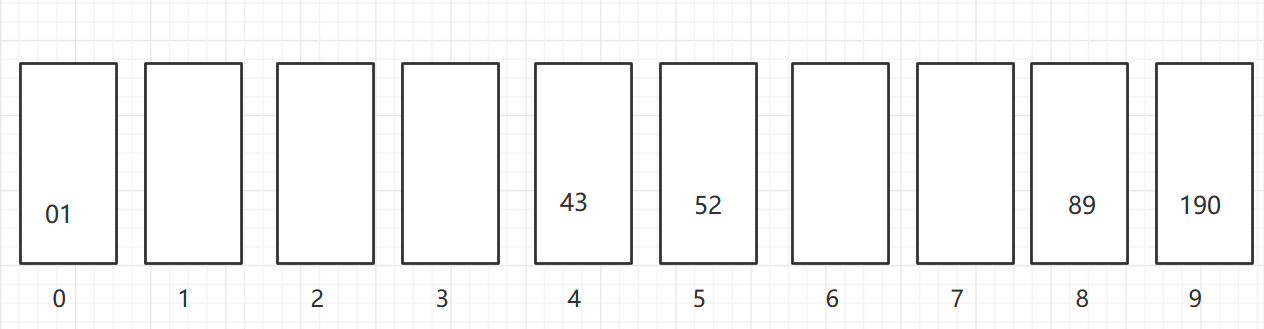
Remove the elements from the bucket in turn
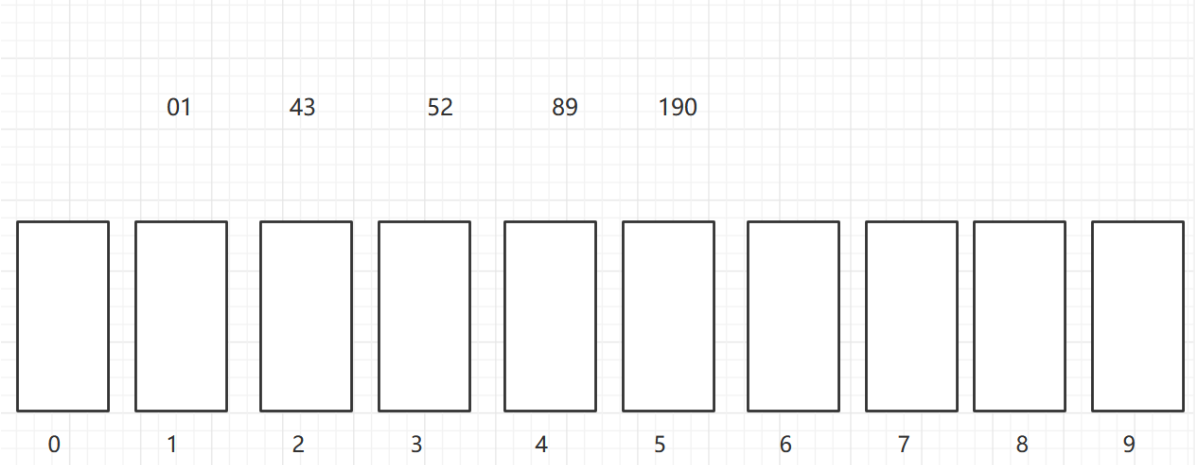
Place 100 digits in the corresponding bucket, and fill in 0 before digits and 10 digits
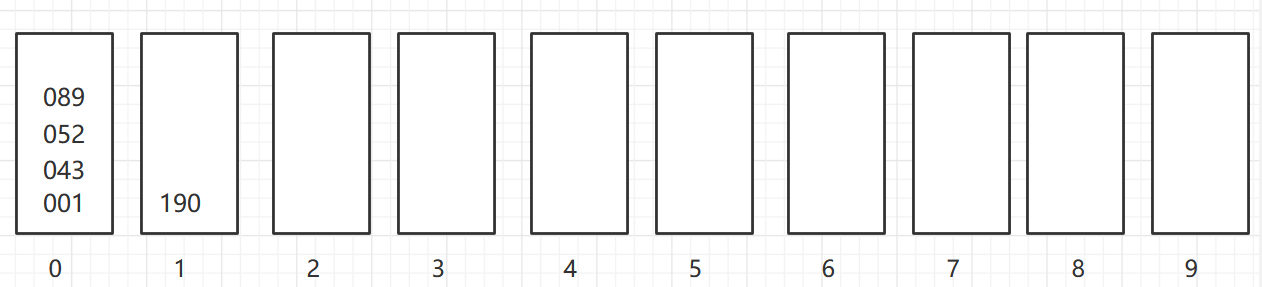
Remove the elements from the bucket in turn

Place in the corresponding bucket according to the thousand digits, and add 0 before the digits, 10 digits and 100 digits
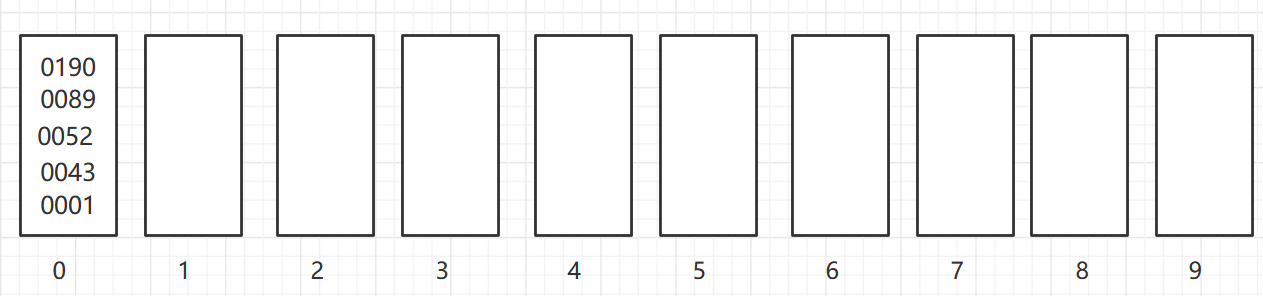
When all numbers are in bucket 0, the elements are taken out in turn, and the order is the order after which they are arranged
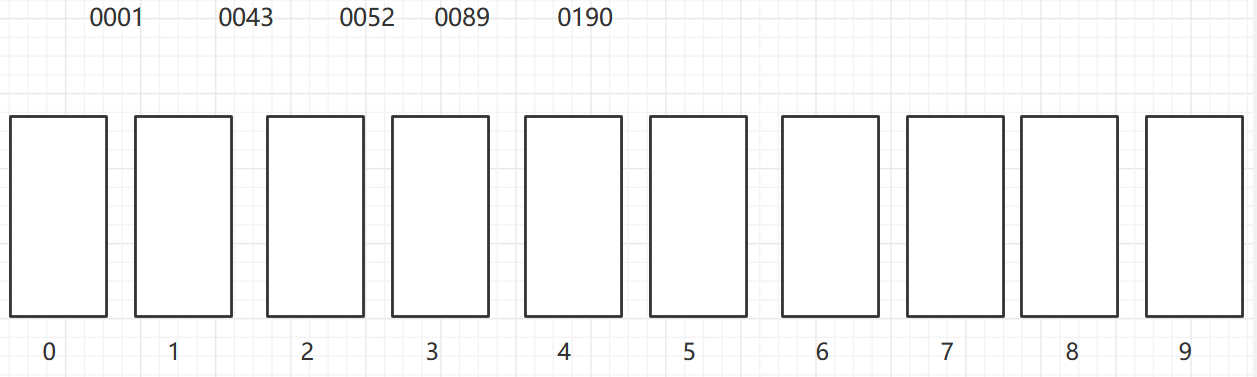
Code:
public class RadixSort {
public static void main(String[] args) {
int arr[] = {53,3,542,748,14,214};
raidxSort(arr);
}
//Cardinality sorting method
public static void raidxSort(int arr[]) {
//Gets the number of digits of the largest number in the array
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
//Get the maximum number of bits
int maxLength = (max + "").length();
//Round 1 (sorting for bits per element)
//Define a two-dimensional array to represent 10 buckets, and each bucket is a two-dimensional array
//1. A two-dimensional array contains 10 one-dimensional arrays
//2. To prevent data overflow when placing numbers, set the size of each one-dimensional array (bucket) to arr.length
//3. Cardinal Sorting is a classical algorithm that uses space to exchange time
int [][] bucket = new int[10][arr.length];
//To record how much data is actually stored in each bucket, we define a one-dimensional array to record the number of data each bucket puts in.
int[] bucketElementCounts = new int[10];
for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {
//Sort the corresponding bits for each element (first bits, second ten bits, third hundred bits...)
for (int j = 0; j < arr.length; j++) {
//Take out the values for each element
int digitOfElement = arr[j] / n % 10;
//Place in the appropriate bucket
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
bucketElementCounts[digitOfElement]++;
}
//In the order of this bucket (the subscripts of a one-dimensional array take out the data and put it in the original array)
int index = 0;
//Traverse through each bucket and put the data in the bucket into the original array
for (int k = 0 ; k < bucketElementCounts.length; k++) {
//Determine if there is data in the bucket
if (bucketElementCounts[k] != 0) {
//Circulate the bucket, that is, the kth bucket
for (int l = 0; l < bucketElementCounts[k]; l++) {
//Remove the element and place it in arr
arr[index++] = bucket[k][l];
}
}
//Each bucketElementCounts[k]=0 barrels with 0 elements after round i+1
bucketElementCounts[k] = 0;
}
System.out.println("No." + (i+1) + "Rear wheel:" + Arrays.toString(arr));
}
}
}
Run result:
After Round 1:[542, 53, 3, 14, 214, 748] After Round 2:[3, 14, 214, 542, 748, 53] After Round 3:[3, 14, 53, 214, 542, 748] Process finished with exit code 0
11. Heap Sorting
Basic Introduction
-
Heap sorting is a sort algorithm designed with heap as the data structure. Heap sorting is an optional sort with the worst, best, and average time complexity of O(nlogn). It is also an unstable sort.
-
A heap is a complete binary tree with the following properties:
-
Each node has a value greater than or equal to the value of its left and right child nodes, called
Top heap
Note: There is no size relationship between the left child's value and the right child's value requiring the node
-
Each node has a value that is less than or equal to the value of its left and right child nodes, called a small top heap
-
-
Large-top heap for general ascending sort and small-top heap for descending sort
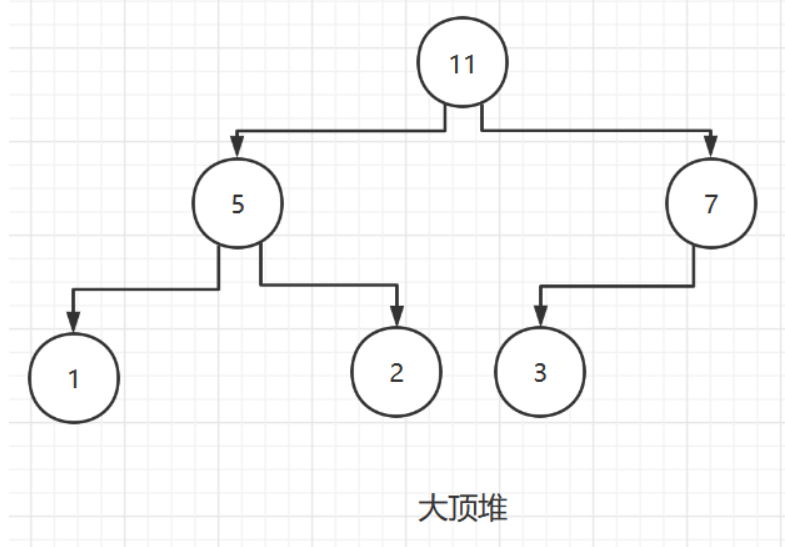
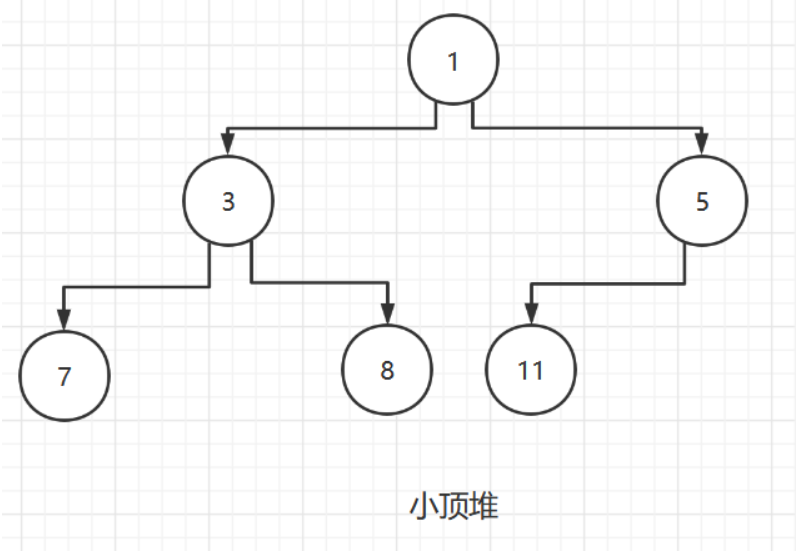
Step one constructs the initial heap. Constructs a large top heap for a given disordered sequence (generally large top heap for ascending and small top heap for descending). Original Array [4,6,8,5,9]
1. Assume that a given disordered sequence structure is as follows
2. At this point, we start with the last non-leaf node (the leaf node naturally does not need to be adjusted, the first non-leaf node arr.length/2-1=5/2-1=1, that is, the following six nodes), adjusting from left to right, from top to bottom
3. A second non-leaf node 4 was found because the 9 elements in [4,9,8] were the largest, and 4 and 9 exchanged.
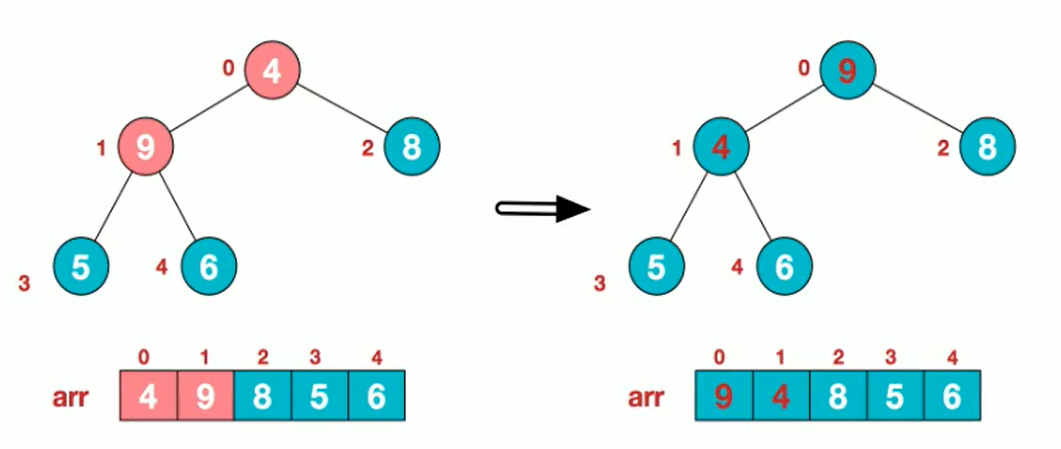
4. At this time, the exchange caused the sub-root [4,5,6] to be structurally chaotic, and continued to adjust, [4,5,6] had the largest 6, and [4,5,6] had the largest 4 and 6 exchanges.
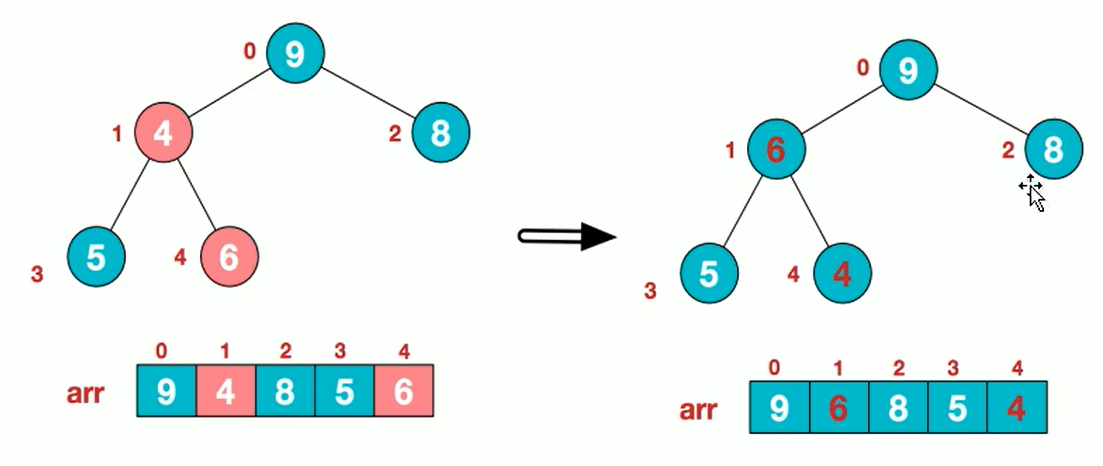
At this point, we construct an unordered sequence into a large top heap
Step 2 swaps the top and end elements of the heap to maximize the end elements. Then continue adjusting the heap and swap the top and end elements to get the second largest element. Exchange, rebuild, exchange so repeatedly.
1. Swap top and end elements 9
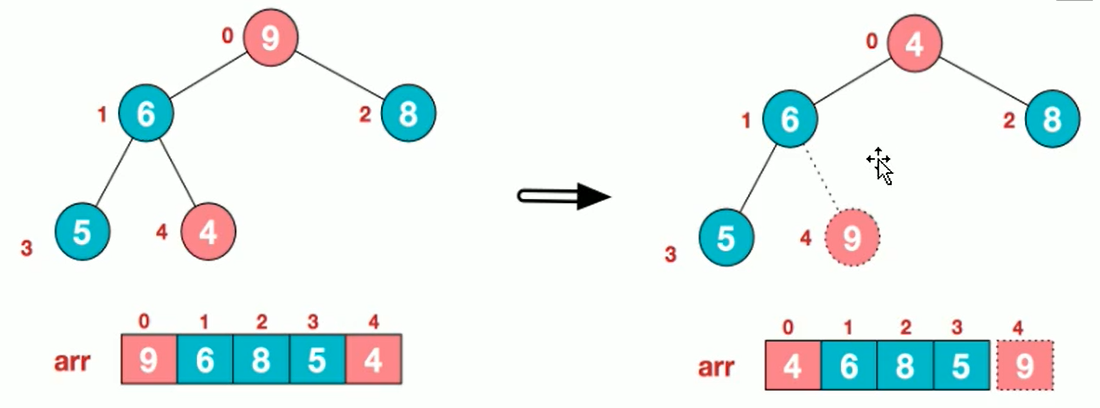
2. Re-adjust the structure to continue meeting the heap definition
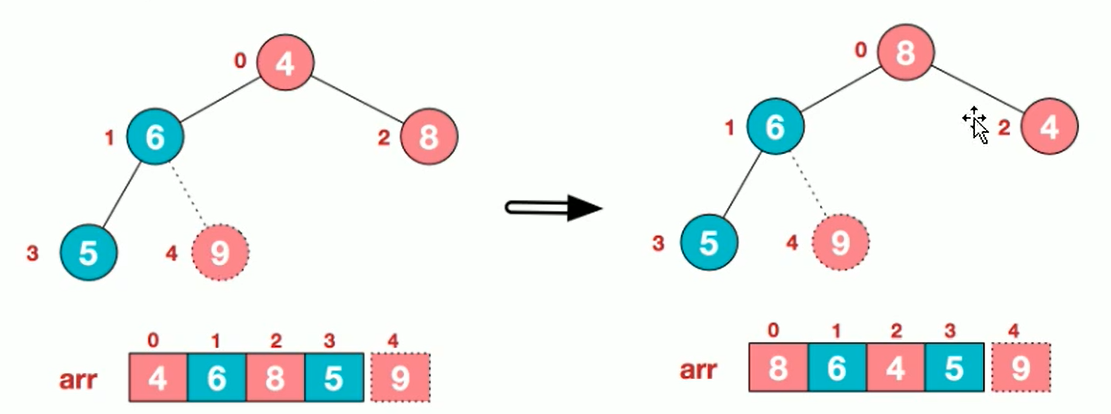
3. The top and end elements 8 are exchanged to get the second largest element 8.
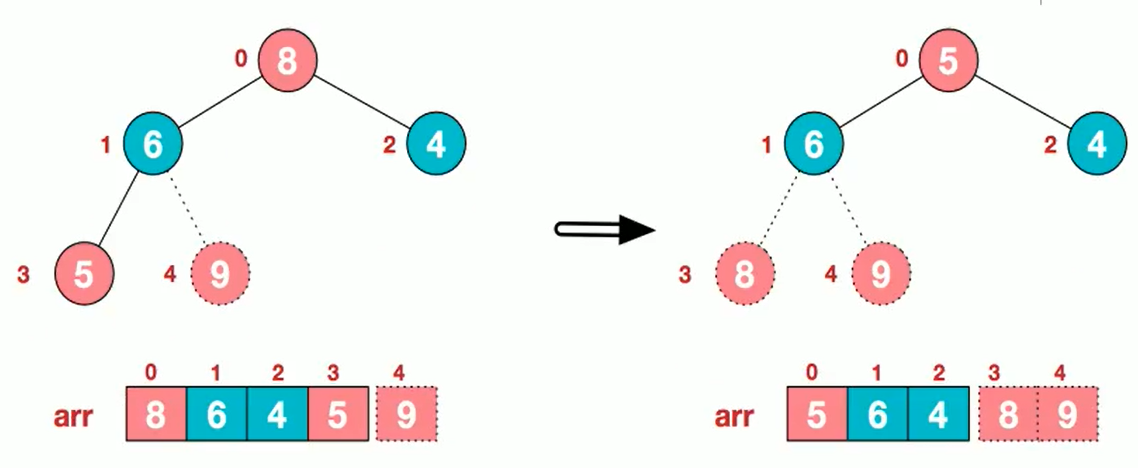
4. Follow-up process, continue adjusting, exchanging, and doing so repeatedly, eventually ordering the entire sequence
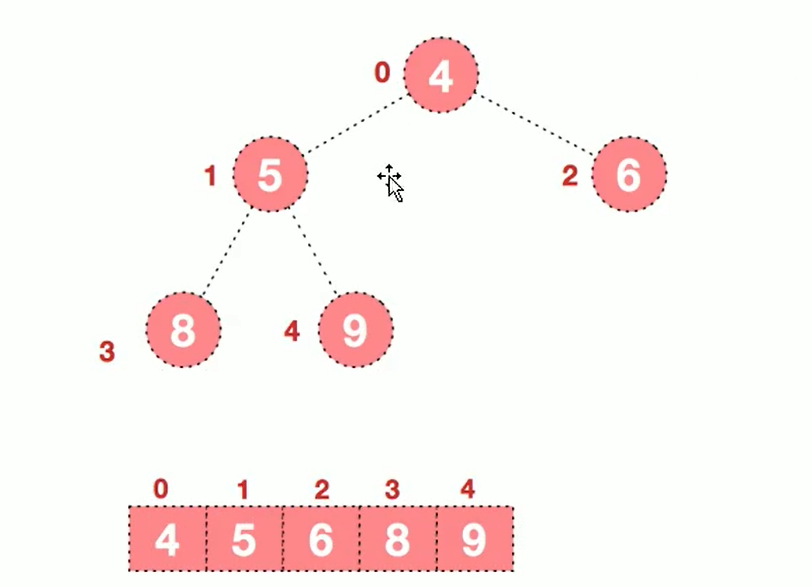
Sorting ideas
- A heap is a tree structure, but heaps are stored sequentially (into an array structure) in a sort
- Build an unordered sequence into a heap and select a large or small top heap based on ascending and descending requirements
- Swap heap top elements with end elements and "sink" the maximum elements to the end of the array
- Re-adjust the structure so that it satisfies the heap definition, then continue swapping heap top elements with current end elements, repeating the adjustment+swap steps until the entire sequence is ordered
Code:
public class Demo2 {
public static void main(String[] args) {
int[] arr = {4, 6, 8, 5, 9};
//Heap Sorting
heapSort(arr);
System.out.println("Result after heap sorting");
System.out.println(Arrays.toString(arr));
}
/**
* Heap Sort (Ascending Sort)
* @param arr Array to Sort
*/
public static void heapSort(int[] arr) {
for(int i=arr.length-1; i>=0; i--) {
//Adjust the array to a large top heap, the length of the unsorted array
for(int j=arr.length/2-1; j>=0; j--) {
adjustHeap(arr, j, i+1);
}
//After adjustment, the first element of the array is the maximum value, and is exchanged for the element
int temp = arr[i];
arr[i] = arr[0];
arr[0] = temp;
}
}
/**
* Adjust the unordered array to a large top heap
* @param arr Array to adjust
* @param index Index of non-leaf nodes
* @param length Length of array to be adjusted
*/
public static void adjustHeap(int[] arr, int index, int length) {
//Save the values of non-leaf nodes, and finally swap
int temp = arr[index];
//Adjust operation
//index*2+1 represents its left subtree
for(int i = index*2+1; i<length; i = i*2+1) {
//If a right subtree exists and the value of the right subtree is greater than the left subtree, point the index to its right subtree
if(i+1<length && arr[i] < arr[i+1]) {
i++;
}
//If the value of the right subtree is greater than the value of the node, the values of the index index are swapped and changed
if(arr[i] > arr[index]) {
arr[index] = arr[i];
index = i;
}else {
break;
}
//After adjustment, place temp in the final adjusted position
arr[index] = temp;
}
}
}
Run result:
Result after heap sorting [4, 5, 6, 8, 9]
6. Search
1. Linear Search
Linear search is a very simple way to find. The search idea is to start from one element of the array, compare one place to the value you are looking for, and return the subscript of the element if you find the same element. Reverse to -1 (not found)
public class Demo1 {
public static void main(String[] args) {
int[] arr = {1, 11, -1, 0, 55};
int result = seqSearch(arr, 1);
if(result == -1) {
System.out.println("The element is not in the array");
}else {
System.out.println("The subscript of the element in the array is:" + result);
}
}
/**
* Linear Lookup
* @param arr Find Array
* @param num Numbers to Find
* @return Index of Numbers
*/
public static int seqSearch(int[] arr, int num) {
for(int i = 0; i<arr.length; i++) {
if(arr[i] == num) {
return i;
}
}
return -1;
}
}
2. Binary Search
Binary lookup must be an ordered array
- Set a variable mid, mid=(left + right)/2 that points to the subscript of the intermediate element
- Compare elements to find with elements of array mid subscript
- If the element found is greater than arr[mid], the left becomes the subscript of the element following mid
- If the element found is less than arr[mid], right becomes the subscript of the previous element in mid
- If the element you are looking for equals arr[mid], mid is where you are looking for the element
- When left > right, the element is not in the array
Code:
public class BinarySearch {
public static void main(String[] args) {
//Finding arrays using binary must be ordered
int arr[] = {1,8,10,89,1000,1234};
int resIndex = binarySearch(arr, 0, arr.length - 1, 8);
System.out.println("resIndex = "+resIndex);
}
/**
* Binary search algorithm
* @param arr array
* @param left Index on the left
* @param right Index on the right
* @param finaVal Value to find
* @return Return Subscript If Found Return-1 Not Found
*/
public static int binarySearch(int[] arr, int left, int right, int finaVal) {
//When left > right, the entire recursive array is not found
if (left > right) {
return -1;
}
int mid = (left + right) / 2;
int midVal = arr[mid];
if (finaVal > midVal) {//Recursion Right
return binarySearch(arr, mid + 1, right, finaVal);
} else if (finaVal < midVal){
return binarySearch(arr, left,mid - 1, finaVal);
} else {
return mid;
}
}
}
However, there may be more than one element to look for. Instead of returning immediately after finding an element, scan the left and right elements, save the subscripts of all the same elements in an array, and return together
public class BinarySearch {
public static void main(String[] args) {
//Finding arrays using binary must be ordered
int arr[] = {1,8,10,89,1000,1000,1000,1234};
List<Integer> resIndexList = binarySearch2(arr, 0, arr.length - 1, 100);
System.out.println("resIndex = "+resIndexList.toString());
}
/**
* {1,8,10,89,1000,1000,1000,1234}
* How to return all values when there are multiple identical values, such as 1000
* 1.Do not return immediately when mid index value is found
* 2.Scan to the left of the mid index value to add subscripts of all elements that satisfy 1000 to the set ArrayList
* 3.Scan to the right of the mid index value to add subscripts of all elements that satisfy 1000 to the set ArrayList
* 4.Return ArrayList
*/
public static List<Integer> binarySearch2(int[] arr, int left, int right, int finaVal) {
//When left > right, the entire recursive array is not found
if (left > right) {
return new ArrayList<>();
}
int mid = (left + right) / 2;
int midVal = arr[mid];
if (finaVal > midVal) {//Recursion Right
return binarySearch2(arr, mid + 1, right, finaVal);
} else if (finaVal < midVal){
return binarySearch2(arr, left,mid - 1, finaVal);
} else {
ArrayList<Integer> resIndexList = new ArrayList<>();
//Scanning to the left of the mid index value adds subscripts to the set ArrayList for all elements that satisfy 1000
int temp = mid - 1;
while (true) {
if (temp < 0 || arr[temp] != finaVal) {
break;
}
//Otherwise put temp in ArrayList
resIndexList.add(temp);
temp -= 1;
}
resIndexList.add(mid);
//Scanning to the right of the mid index value adds subscripts to the set ArrayList for all elements that satisfy 1000
temp = mid + 1;
while (true) {
if (temp > arr.length - 1 || arr[temp] != finaVal) {
break;
}
//Otherwise put temp in ArrayList
resIndexList.add(temp);
temp += 1;
}
return resIndexList;
}
}
}
3. Interpolation lookup
In a binary search, if the element we are looking for is at the front or last segment of the array, the search efficiency is very low. So in Binary Search First, interpolation lookup is introduced, which is also a search method based on ordered arrays.
The difference between interpolation lookup and binary lookup is that interpolation lookup uses an adaptive algorithm that calculates mid.
The mid value is calculated in two search algorithms:
-
Binary lookup: mid = (left + right)/2
-
Interpolation lookup:
mid = left + (right - left) * (num - arr[left]) / (arr[right] - arr[left])
- Where num is the value to find
Interpolation lookup considerations:
- Interpolation is faster for lookup tables with large amounts of data and uniform keyword distribution
- This method is not necessarily better than half-search when keywords are not evenly distributed
public class InsertValueSearch {
public static void main(String[] args) {
int arr[] = {1,8,10,89,1000,1000,1000,1234};
int resIndex = insertValueSearch(arr, 0, arr.length - 1, 89);
System.out.println("resIndex = "+resIndex);
}
/**
* The interpolation lookup algorithm also requires the array to be ordered
* @param arr array
* @param left Left Index
* @param right Right Index
* @param findVal Lookup Value
* @return Return Subscript If Found Return-1 Not Found
*/
public static int insertValueSearch(int[] arr, int left, int right, int findVal) {
if (left > right || findVal < arr[0] || findVal > arr[arr.length - 1]) {
return -1;
}
//Find mid
int mid = left + (right - left) * (findVal - arr[left]) / (arr[right] - arr[left]);
int midVal = arr[mid];
if (findVal > midVal) {//Explanation should recurse to the right
return insertValueSearch(arr, mid + 1, right, findVal);
} else if (findVal < midVal) {
return insertValueSearch(arr, left, mid - 1, findVal);
} else {
return mid;
}
}
}
4. Fibonacci (Golden Section) Search
-
A golden section is a line segment that is divided into two parts so that the ratio of one part to the whole length equals the ratio of the other part to the part. The approximation of the first three digits is 0.618. Because the shape designed at this scale is very beautiful, it is called the golden section, also known as the Chinese-foreign ratio.
-
The Fibonacci sequence {1,1,2,3,5,8,13,21,34,55} finds that the ratio of the two adjacent numbers of the Fibonacci sequence is infinitely close to the golden section value of 0.618
The Fibonacci search principle is similar to the first two, except that the position of the intermediate node (mid) is changed. Instead of being intermediate or interpolated, mid is located near the golden section point, which is mid = low + F(k-1)-1 (F stands for the Fibonacci column), as shown in the following figure:
Understanding of F(k-1)-1:
-
From the properties of the Fibonacci sequence F[k]=F[k-1]+F[k-2], you can get (F[k]-1) = (F[k-1]-1) + (F[k-2]-1) + 1, which states that if the length of the sequence table is F[k]-1, it can be divided into two ends of the length F[k-1]-1 and F[k-2]-1, as shown in the figure above, so that the middle position is F[low+F(k-1)-1
-
Similarly, each field can be split in the same way
-
However, the length n of the sequence table does not necessarily equal F[k]-1, so you need to increase the length n of the original sequence table to F[k]-1, where the k-value can be obtained from the following code as long as F[k]-1 is exactly greater than or equal to n. When the length of the sequence table is increased, the new position (from n+1 to F[k]-1) is assigned the value of n position.
//Gets the subscript of the Fibonacci split value
while (high > f[k] - 1) {
k++;
}
public class FeibonacciSearch {
public static int maxSize = 20;
public static void main(String[] args) {
int arr[] = {1,8,10,89,1000,1000,1000,1234};
System.out.println(fibSearch(arr, 1234));
}
//Because mid = low + F(k - 1) - 1 after that, you need to use the Fibonacci series, so you need to create one
public static int[] fib() {
int[] f = new int[maxSize];
f[0] = 1;
f[1] = 1;
for (int i = 2; i < maxSize; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
//Writing Fibonacci Search Algorithms
/**
*
* @param a array
* @param key The keys (values) we need to find
* @return Return the corresponding subscript without -1
*/
public static int fibSearch(int[] a, int key){
int low = 0;
int high = a.length - 1;
int k = 0;//Subscript representing the Fibonacci split value
int mid = 0;//Store mid value
int f[] = fib();//Get the Fibonacci series
//Gets the subscript of the Fibonacci split value
while (high > f[k] - 1) {
k++;
}
//Because the f[k] value may be larger than the length of a, we need to use the Arrays class to construct a new array and point to a[]
//Insufficient parts will be filled with 0
int[] temp = Arrays.copyOf(a, f[k]);
//You actually need to populate temp with the last number of a arrays
//Example temp={1,8,10,89,1000,1234,0,0} => {1,8,10,89,1000,1234,1234}
for (int i = high + 1; i < temp.length; i++) {
temp[i] = a[high];
}
//Using the while loop, find our number key s
while (low <= high) {
mid = low + f[k - 1] - 1;
if (key < temp[mid]) {//Look to the left of the array
high = mid - 1;
k--;
} else if (key > temp[mid]) {//Look to the right of the array
low = mid + 1;
k -= 2;
} else {
if (mid <= high) {
return mid;
} else {
return high;
}
}
}
return -1;
}
}
7. Hash Table
1. Basic Introduction
A Hash table is a data structure that is directly accessed based on a key value. That is, it accesses records by mapping key code values to a location in the table to speed up the search. This mapping function is called a hash function, and the array of records is called a hash list.
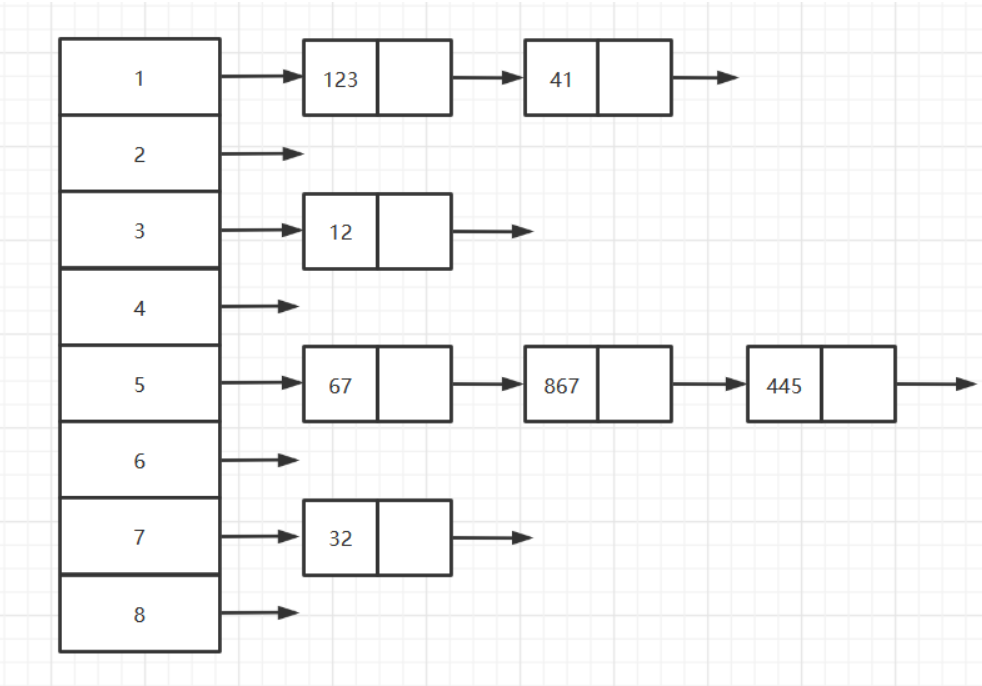
Code:
public class HashTabDemo {
public static void main(String[] args) {
//Create Students
Student student1 = new Student(1, "Nyima");
Student student2 = new Student(2, "Lulu");
Student student6 = new Student(6, "WenWen");
HashTab hashTab = new HashTab(5);
hashTab.add(student1);
hashTab.add(student2);
hashTab.add(student6);
hashTab.traverse();
//Find student information by id
hashTab.findStuById(6);
}
}
class Student {
int id;
String name;
Student next;
public Student(int id, String name) {
this.id = id;
this.name = name;
}
@Override
public String toString() {
return "Student{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
}
class LinkedList {
private Student head = new Student(-1, "");
/**
* Insert Student Information
* @param student Insert student information
*/
public void add(Student student) {
if(head.next == null) {
head.next = student;
return;
}
Student temp = head.next;
while(temp.next != null) {
temp = temp.next;
}
temp.next = student;
}
/**
* Traversing a list of chains
*/
public void traverse() {
if(head.next == null) {
System.out.println("Chain list is empty");
return;
}
Student temp = head;
while(temp.next != null) {
temp = temp.next;
System.out.print(temp + " ");
}
//Line Break
System.out.println();
}
/**
* Find student information by id
* @param id Student id
*/
public void findStuById(int id) {
if(head.next == null) {
System.out.println("Chain list is empty");
return;
}
Student temp = head;
while(temp.next != null) {
temp = temp.next;
if(temp.id == id) {
//Find students, print student information
System.out.println("The student information:" + temp);
return;
}
}
System.out.println("The student information was not found");
}
}
class HashTab {
private LinkedList[] linkedLists;
private final int size;
public HashTab(int size) {
this.size = size;
//Initialize Hash list
linkedLists = new LinkedList[size];
//Initialize each list or a null pointer exception will be thrown
for(int i=0; i<this.size; i++) {
//Initialize each list
linkedLists[i] = new LinkedList();
}
}
public void add(Student student) {
int hashId = getHash(student.id);
linkedLists[hashId].add(student);
}
public void traverse() {
for(int i=0 ; i<size; i++) {
linkedLists[i].traverse();
}
}
public void findStuById(int id) {
int hashId = getHash(id);
linkedLists[hashId].findStuById(id);
}
/**
* Hash function, get hash value
* @param id Student id
* @return Corresponding hash value
*/
private int getHash(int id) {
return id % size;
}
}
Run result:
Chain list is empty
Student{id=1, name='Nyima'} Student{id=6, name='WenWen'}
Student{id=2, name='Lulu'}
Chain list is empty
Chain list is empty
The student information: Student{id=6, name='WenWen'}
Process finished with exit code 0
8. Tree Structure
1. Binary Tree
Why trees are needed
- Array lookup is efficient, but insertion is inefficient.
- Chain list insertion efficiency is high, and lookup efficiency is low.
A data structure is needed to balance the efficiency of lookup and insertion so that both lookup and insertion speeds can be improved, so there is a tree data structure.
Basic concepts of trees
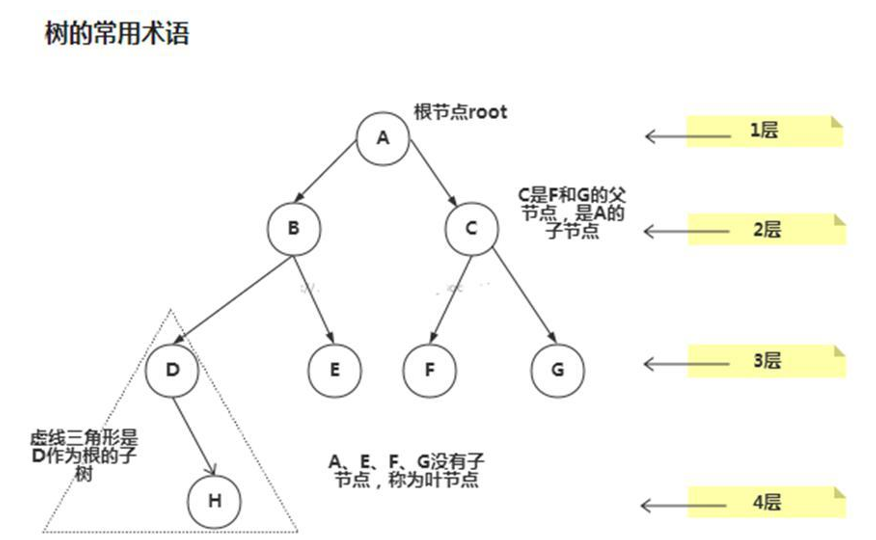
Basic concepts of binary trees
A form in which each node can have at most two children is called a binary tree
Full Binary Tree
If all the leaf nodes of the binary tree are on the last level, and the total number of nodes = 2n-1, n is the number of layers, then we call it a full binary tree.
Complete Binary Tree
If all the leaf nodes of the binary tree are on the last or the second-last level, and the last level is continuous on the left, and the second-last level is continuous on the right, we call it a complete binary tree.
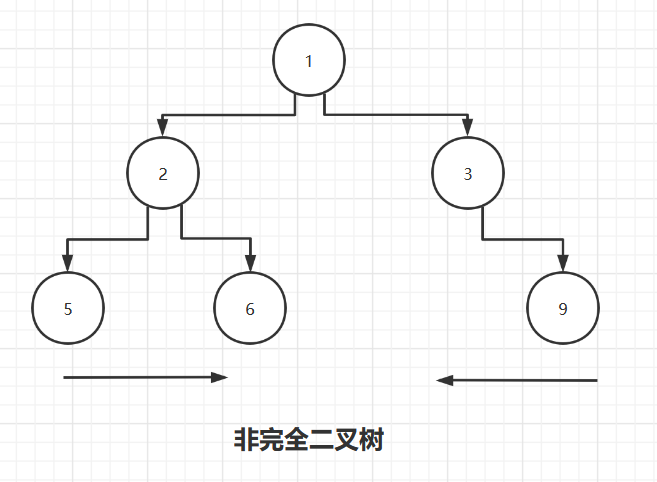
Traversal of Binary Trees
Pre-order traversal
Traverse the parent node first, then the left child node, and finally the right child node
Intermediate traversal
Traverse left child node, parent node, and right child node
Post-order traversal
Traverse left child node, right child node, and parent node
You can see that the difference between before and after is when the parent node traverses
Sketch Map
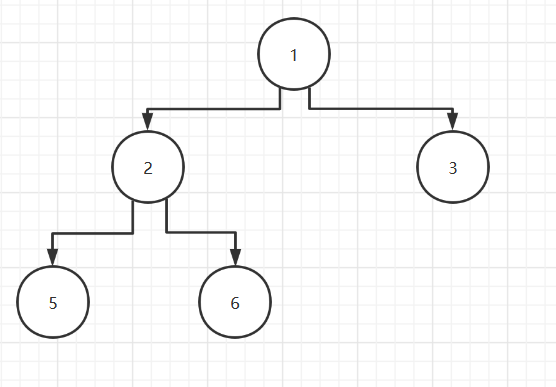
Pre-order traversal results: 1, 2, 5, 6, 3
Intermediate traversal results: 5, 2, 6, 1, 3
Post-order traversal results: 5, 6, 2, 3, 1
Actual Code
This code creates a binary tree manually and traverses it recursively
public class BinaryTreeDemo {
public static void main(String[] args) {
//Create Binary Tree
BinaryTree binaryTree = new BinaryTree();
//Manually create nodes and place them in a binary tree
StuNode stu1 = new StuNode(1, "A");
StuNode stu2 = new StuNode(2, "B");
StuNode stu3 = new StuNode(3, "C");
StuNode stu4 = new StuNode(4, "D");
stu1.setLeft(stu2);
stu1.setRight(stu3);
stu3.setRight(stu4);
binaryTree.setRoot(stu1);
//Traversing Binary Trees
binaryTree.preTraverse();
binaryTree.midTraverse();
binaryTree.lastTraverse();
}
}
class BinaryTree {
/**
* root node
*/
private StuNode root;
public void setRoot(StuNode root) {
this.root = root;
}
public void preTraverse() {
if(root != null) {
System.out.println("Pre-order traversal");
root.preTraverse();
System.out.println();
}else {
System.out.println("The binary tree is empty!");
}
}
public void midTraverse() {
if(root != null) {
System.out.println("Intermediate traversal");
root.midTraverse();
System.out.println();
}else {
System.out.println("The binary tree is empty!");
} }
public void lastTraverse() {
if(root != null) {
System.out.println("Post-order traversal");
root.lastTraverse();
System.out.println();
}else {
System.out.println("The binary tree is empty!");
} }
}
/**
* A node in a binary tree
* Save student information and left and right child information
*/
class StuNode {
int id;
String name;
StuNode left;
StuNode right;
public StuNode(int id, String name) {
this.id = id;
this.name = name;
}
public int getId() {
return id;
}
public void setId(int id) {
this.id = id;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public StuNode getLeft() {
return left;
}
public void setLeft(StuNode left) {
this.left = left;
}
public StuNode getRight() {
return right;
}
public void setRight(StuNode right) {
this.right = right;
}
@Override
public String toString() {
return "StuNode{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
/**
* Pre-order traversal
*/
public void preTraverse() {
//Location of parent node
System.out.println(this);
if(left != null) {
left.preTraverse();
}
if(right != null) {
right.preTraverse();
}
}
/**
* Intermediate traversal
*/
public void midTraverse() {
if(left != null) {
left.midTraverse();
}
//Location of parent node
System.out.println(this);
if(right != null) {
right.midTraverse();
}
}
public void lastTraverse() {
if(left != null) {
left.lastTraverse();
}
if(right != null) {
right.lastTraverse();
}
//Location of parent node
System.out.println(this);
}
}
Run result:
Pre-order traversal
StuNode{id=1, name='A'}
StuNode{id=2, name='B'}
StuNode{id=3, name='C'}
StuNode{id=4, name='D'}
Intermediate traversal
StuNode{id=2, name='B'}
StuNode{id=1, name='A'}
StuNode{id=3, name='C'}
StuNode{id=4, name='D'}
Post-order traversal
StuNode{id=2, name='B'}
StuNode{id=4, name='D'}
StuNode{id=3, name='C'}
StuNode{id=1, name='A'}
Process finished with exit code 0
Iterative implementation
Using iteration to traverse a binary tree is similar to recursion, but you need to maintain a stack for storing nodes yourself
public class Demo5 {
public static void main(String[] args) {
TreeNode node1 = new TreeNode(1);
TreeNode node2 = new TreeNode(2);
TreeNode node3 = new TreeNode(3);
node1.left = node2;
node1.right = node3;
List<Integer> integers = preTraverse(node1);
System.out.println("Pre-order traversal result");
for (Integer integer : integers) {
System.out.print(integer);
System.out.print(" ");
}
System.out.println();
List<Integer> integers2 = midTraverse(node1);
System.out.println("Medium Traversal Results");
for (Integer integer : integers2) {
System.out.print(integer);
System.out.print(" ");
}
System.out.println();
List<Integer> integers3 = lastTraverse(node1);
System.out.println("Post-traversal results");
for (Integer integer : integers3) {
System.out.print(integer);
System.out.print(" ");
}
System.out.println();
}
/**
* Pre-order traversal of binary trees using iteration
* @param root Binary Tree Root Node
* @return Traversed Set
*/
public static List<Integer> preTraverse(TreeNode root) {
// Collection for storing results
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
// Stack, used to store traversed nodes
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
// Traversing Binary Trees
while (!stack.isEmpty()) {
// The top element goes out of the stack and into the collection
root = stack.pop();
result.add(root.val);
// Walk through the right subtree and stack it
if (root.right != null) {
stack.push(root.right);
}
// Traverse left subtree, stack
if (root.left != null) {
stack.push(root.left);
}
}
return result;
}
/**
* Intermediate traversal of binary trees using iteration
* @param root Binary Tree Root Node
* @return Intermediate traversal result set
*/
public static List<Integer> midTraverse(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Stack<TreeNode> stack = new Stack<>();
while (root != null || !stack.isEmpty()) {
// Node stacks and traverses its left subtree
while (root != null) {
stack.push(root);
root = root.left;
}
// The top element of the stack goes out of the stack and into the result set
root = stack.pop();
result.add(root.val);
// Traverse the right subtree of this node
root = root.right;
}
return result;
}
/**
* Post-order traversal using iteration
* @param root Binary Tree Root Node
* @return Post-order Traversal Collection
*/
public static List<Integer> lastTraverse(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Stack<TreeNode> stack = new Stack<>();
// Save the right subtree into the collection to avoid duplication
TreeNode pre = null;
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
// Get top stack element
root = stack.pop();
// If the element does not have a right subtree, or if the right subtree has been nearly traversed, place it in the collection
if (root.right == null || root.right == pre) {
result.add(root.val);
pre = root;
root = null;
} else {
// Otherwise, continue traversing the right subtree of the node
stack.push(root);
root = root.right;
}
}
return result;
}
}
Run result:
Pre-order traversal result
1 2 3
Medium Traversal Results
2 1 3
Post-traversal results
2 3 1
Finding Binary Trees
The thinking of searching before, during and after is similar to traversal, when corresponding elements are found, it is OK to return directly.
Code:
public class Demo2 {
public static void main(String[] args) {
//Create Root Node
BinarySearchTree tree = new BinarySearchTree();
//Manually create nodes
Student student1 = new Student(1, "A");
Student student2 = new Student(2, "B");
Student student3 = new Student(3, "C");
Student student4 = new Student(4, "D");
Student student5 = new Student(5, "E");
student1.setLeft(student2);
student1.setRight(student3);
student2.setLeft(student4);
student3.setRight(student5);
//Specify Root Node
tree.setRoot(student1);
//lookup
tree.preSearch(3);
tree.midSearch(4);
tree.lastSearch(7);
}
}
class BinarySearchTree {
private Student root;
public void setRoot(Student root) {
this.root = root;
}
public void preSearch(int id) {
System.out.println("Preorder Search");
if(root == null) {
System.out.println("The tree is empty!");
return;
}
Student result = root.preSearch(id);
if(result == null) {
System.out.println("The element was not found");
System.out.println();
return;
}
System.out.println(result);
System.out.println();
}
public void midSearch(int id) {
System.out.println("Search in Middle Order");
if(root == null) {
System.out.println("The tree is empty!");
return;
}
Student result = root.midSearch(id);
if(result == null) {
System.out.println("The element was not found");
System.out.println();
return;
}
System.out.println(result);
System.out.println();
}
public void lastSearch(int id) {
System.out.println("Find in Postorder");
if(root == null) {
System.out.println("The tree is empty!");
return;
}
Student result = root.lastSearch(id);
if(result == null) {
System.out.println("The element was not found");
System.out.println();
return;
}
System.out.println(result);
System.out.println();
}
}
class Student {
int id;
String name;
Student left;
Student right;
public Student(int id, String name) {
this.id = id;
this.name = name;
}
public int getId() {
return id;
}
public void setId(int id) {
this.id = id;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public Student getLeft() {
return left;
}
public void setLeft(Student left) {
this.left = left;
}
public Student getRight() {
return right;
}
public void setRight(Student right) {
this.right = right;
}
@Override
public String toString() {
return "Student{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
/**
* Preorder Search
* @param id Student id to find
* @return Students Found
*/
public Student preSearch(int id) {
//If found, return
if(this.id == id) {
return this;
}
//Find in the left subtree and return if found
Student student = null;
if(left != null) {
student = left.preSearch(id);
}
if(student != null) {
return student;
}
//Find in the right subtree and return whether or not you find it
if(right != null) {
student = right.preSearch(id);
}
return student;
}
/**
* Search in Middle Order
* @param id Student id to find
* @return Students Found
*/
public Student midSearch(int id) {
Student student = null;
if(left != null) {
student = left.midSearch(id);
}
if(student != null) {
return student;
}
//Find it and return
if(this.id == id) {
return this;
}
if(right != null) {
student = right.midSearch(id);
}
return student;
}
/**
* Find in Postorder
* @param id Student id to find
* @return Students Found
*/
public Student lastSearch(int id) {
Student student = null;
if(left != null) {
student = left.lastSearch(id);
}
if(student !=null) {
return student;
}
if(right != null) {
student = right.lastSearch(id);
}
if(this.id == id) {
return this;
}
return student;
}
}
Run result:
Preorder Search
Student{id=3, name='C'}
Search in Middle Order
Student{id=4, name='D'}
Find in Postorder
The element was not found
Deletion of Binary Trees
Delete Requirements
- If the leaf node is deleted, delete it directly
- If a non-leaf node is deleted, the subtree is deleted
Delete ideas
- Because our binary tree is unidirectional, we are able to determine if the child node of the current node needs to be deleted, rather than whether the current node needs to be deleted.
- If the left subnode of the current node is not empty and the left subnode is to delete the node, this will be done. Left = null; And returns (end recursive deletion)
- If the right sub-node of the current node is not empty and the right sub-node is to delete the node, it will be this.right= null; And returns (end recursive deletion)
- If steps 2 and 3 do not delete the node, we need to recursively delete it to the left subtree
- If you did not delete the node in step 4, you should recursively delete it to the right subtree
public class Demo3 {
public static void main(String[] args) {
//Create Root Node
BinaryDeleteTree deleteTree = new BinaryDeleteTree();
//Manually create nodes
StudentNode student1 = new StudentNode(1, "A");
StudentNode student2 = new StudentNode(2, "B");
StudentNode student3 = new StudentNode(3, "C");
StudentNode student4 = new StudentNode(4, "D");
StudentNode student5 = new StudentNode(5, "E");
student1.setLeft(student2);
student1.setRight(student3);
student2.setLeft(student4);
student3.setRight(student5);
//Specify Root Node
deleteTree.setRoot(student1);
//Delete Node
deleteTree.deleteNode(3);
}
}
class BinaryDeleteTree {
StudentNode root;
public void setRoot(StudentNode root) {
this.root = root;
}
/**
* Delete Node
* @param id Delete node id
*/
public void deleteNode(int id) {
System.out.println("Delete Node");
if(root.id == id) {
root = null;
System.out.println("Root node deleted");
return;
}
//Call Delete Method
root.deleteNode(id);
}
}
class StudentNode {
int id;
String name;
StudentNode left;
StudentNode right;
public StudentNode(int id, String name) {
this.id = id;
this.name = name;
}
public int getId() {
return id;
}
public void setId(int id) {
this.id = id;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public StudentNode getLeft() {
return left;
}
public void setLeft(StudentNode left) {
this.left = left;
}
public StudentNode getRight() {
return right;
}
public void setRight(StudentNode right) {
this.right = right;
}
@Override
public String toString() {
return "StudentNode{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
/**
* Delete Node
* @param id Delete node id
*/
public void deleteNode(int id) {
//If the left subtree is not empty and the node to be found, delete it
if(left != null && left.id == id) {
left = null;
System.out.println("Delete succeeded");
return;
}
//If the right subtree is not empty and the node to be found, delete it
if(right != null && right.id == id) {
right = null;
System.out.println("Delete succeeded");
return;
}
//Left recursion, continue search
if(left != null) {
left.deleteNode(id);
}
//Right Recursion, Continue Searching
if(right != null) {
right.deleteNode(id);
}
}
}
Sequential Storage Binary Tree
Basic description
From the point of view of data storage, the storage of arrays and trees can be converted to each other, that is, arrays can be converted to trees and trees can also be converted to arrays.
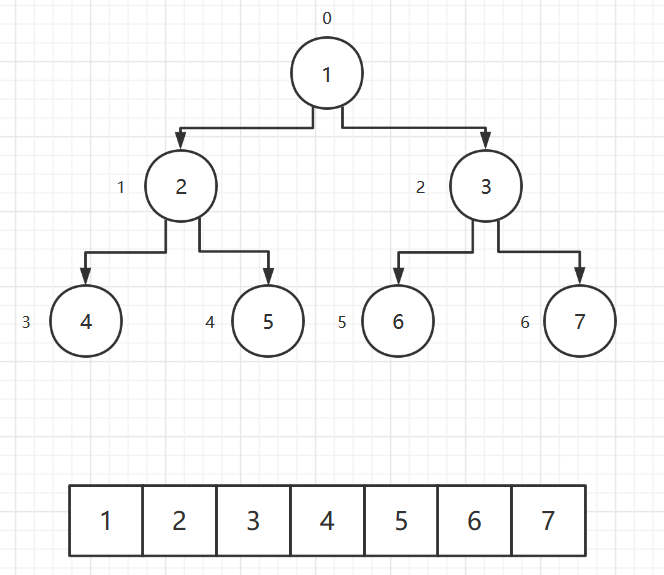
Characteristic
- Ordered binary trees usually consider only complete binary trees
- The left child node of the nth element is 2 × n + 1
- The right child node of the nth element is 2 × n + 2
- The parent node of the nth element is (n-1)2
- Where n denotes the number of elements in a binary tree (numbering starts at 0)
Traversing is similar to traversing a binary tree, except that the conditions for recursion are different
Implementation Code
public class Demo4 {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6, 7};
ArrBinaryTree arrBinaryTree = new ArrBinaryTree(arr);
//Pre-order traversal
System.out.println("Array Preorder Traversal");
arrBinaryTree.preTraverse();
System.out.println();
//Intermediate traversal
System.out.println("Ordinal traversal in arrays");
arrBinaryTree.midTraverse();
System.out.println();
//Post-order traversal
System.out.println("Post-Array Traversal");
arrBinaryTree.lastTraverse();
System.out.println();
}
}
class ArrBinaryTree {
int[] arr;
final int STEP = 2;
public ArrBinaryTree(int[] arr) {
this.arr = arr;
}
/**
* Pre-order traversal of arrays
*/
public void preTraverse() {
preTraverse(0);
}
/**
* Pre-order traversal of arrays
* @param index Traversed array element Subscripts
*/
private void preTraverse(int index) {
if(arr == null || arr.length == 0) {
System.out.println("The array is empty!");
return;
}
System.out.print(arr[index] + " ");
//Recursion Left
if((index * STEP) + 1 < arr.length) {
preTraverse((index * STEP) + 1);
}
//Recursion Right
if((index * STEP) + 2 < arr.length) {
preTraverse((index * STEP) + 2);
}
}
public void midTraverse() {
midTraverse(0);
}
private void midTraverse(int index) {
if(arr == null || arr.length == 0) {
System.out.println("The array is empty!");
}
//Left Recursion
if((index * STEP) + 1 < arr.length) {
midTraverse((index * STEP) + 1);
}
System.out.print(arr[index] + " ");
//Right Recursion
if((index * STEP) + 2 < arr.length) {
midTraverse((index * STEP) + 2);
}
}
public void lastTraverse() {
lastTraverse(0);
}
private void lastTraverse(int index) {
if(arr == null || arr.length == 0) {
System.out.println("The array is empty!");
}
//Left Recursion
if((index * STEP) + 1 < arr.length) {
lastTraverse((index * STEP) + 1);
}
//Right Recursion
if((index * STEP) + 2 < arr.length) {
lastTraverse((index * STEP) + 2);
}
System.out.print(arr[index] + " ");
}
}
Run result:
Array Preorder Traversal 1 2 4 5 3 6 7 Ordinal traversal in arrays 4 2 5 1 6 3 7 Post-Array Traversal 4 5 2 6 7 3 1
Threaded Binary Tree
Basic concepts
Because of the general binary tree, the left and right pointers of the leaf nodes are empty, which causes a waste of space. To reduce waste, you have threaded binary trees
- The binary chain list of N nodes contains n+1 (formula 2n-(n-1)=n+1) null pointer domains. A null pointer field in a binary list is used to store pointers to the precursor and subsequent nodes of the node in a traversal order (this additional pointer is called a "thread")
- This list of binary chains with threads is called a list of threads, and the corresponding binary trees are called threaded binary trees. Depending on the nature of the threads, threaded binary trees can be divided into three types: pre-ordered threaded binary tree, middle-ordered threaded binary tree and post-ordered threaded binary tree.
- The preceding node of a node, called a precursor node
- The next node of a node, called a successor node
- If a node already has left and right children, the node cannot be threaded, so after threading a binary tree, the left and rights of the node are in two cases
- Left may point to a left child or to a precursor node
- Right may point to a right child or to a successor node
graphic
Before Intermediate Threading
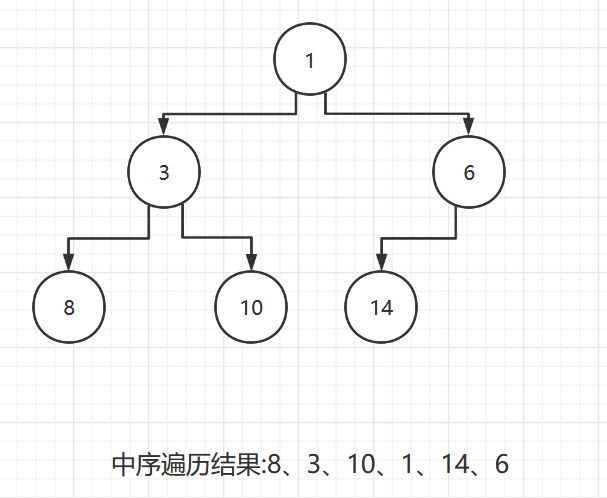
After Intermediate Threading
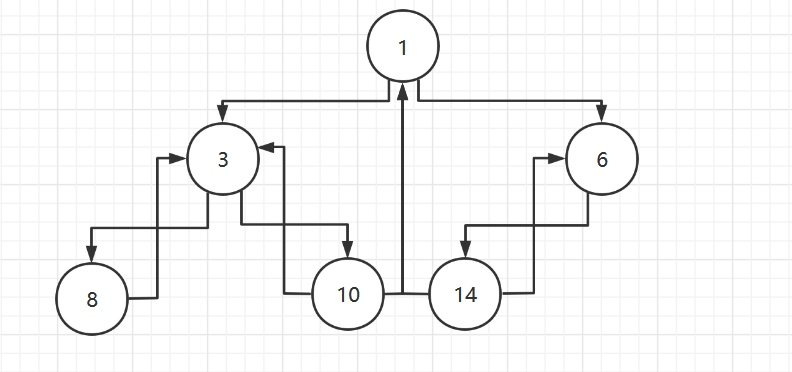
Implementation Code
Threaded thinking
- Each node needs two variables to represent the type of left and right pointers (preserve left and right subtrees or precursors and successors)
- Two variables are required to represent the current node and the precursor node of the current node
- Binding a precursor node by pointing its left pointer at the precursor node
- Binding succeeding nodes by pointing the right pointer of the precursor node to the current node
Traversal mode
- Nodes can be traversed linearly without recursion
- First there is an outer loop, instead of a recursive operation, the temporary node of the loop condition is not empty
- The first inner loop finds the first element and prints it
- The second loop finds the successor elements of a node
- Finally, make the temporary node the right child
public class Demo1 {
public static void main(String[] args) {
//Initialize Node
Student student1 = new Student(1, "1");
Student student2 = new Student(2, "3");
Student student3 = new Student(3, "6");
Student student4 = new Student(4, "8");
Student student5 = new Student(5, "10");
Student student6 = new Student(6, "14");
//Manually create a binary tree
ThreadedBinaryTree tree = new ThreadedBinaryTree();
student1.setLeft(student2);
student1.setRight(student3);
student2.setLeft(student4);
student2.setRight(student5);
student3.setLeft(student6);
tree.setRoot(student1);
tree.midThreaded();
//Get the precursor and successor nodes of the fifth node
System.out.println("The precursor and successor nodes of the fifth node");
System.out.println(student5.getLeft());
System.out.println(student5.getRight());
//Traversing Threaded Binary Trees
System.out.println("Traversing Threaded Binary Trees");
tree.midThreadedTraverse();
}
}
class ThreadedBinaryTree {
private Student root;
/**
* Point to the previous node of the current node
*/
private Student pre;
public void setRoot(Student root) {
this.root = root;
}
/**
* Intermediate threading
* @param node Current Node
*/
private void midThreaded(Student node) {
if(node == null) {
return;
}
//Left threading
midThreaded(node.getLeft());
//Threaded Current Node
//If the left pointer of the current node is empty, point to the precursor node and change the left pointer type
if(node.getLeft() == null) {
node.setLeft(pre);
node.setLeftType(1);
}
//Set the value of the right pointer to the successor node by the precursor node
if(pre != null && pre.getRight() == null) {
pre.setRight(node);
pre.setRightType(1);
}
//After processing a node, make the current node the precursor of the next node
pre = node;
//Right Threaded
midThreaded(node.getRight());
}
public void midThreaded() {
midThreaded(root);
}
/**
* Traversing threaded binary trees
*/
public void midThreadedTraverse() {
//Staging traversed node
Student tempNode = root;
//Non-recursive method traversal, loop if tempNode is not empty
while(tempNode != null) {
//Visit the left subtree of the binary tree until the left subtree of a node points to the preceding node
while(tempNode.getLeftType() != 1) {
tempNode = tempNode.getLeft();
}
//First node found
System.out.println(tempNode);
//Visit the node's right subtree again to see if subsequent nodes are saved
//If so, print the successor node information for the node
while(tempNode.getRightType() == 1) {
tempNode = tempNode.getRight();
System.out.println(tempNode);
}
tempNode = tempNode.getRight();
}
}
}
class Student {
private int id;
private String name;
private Student left;
private Student right;
/**
* The type of left and right pointers, 0--> points to left and right children, 1--> points to precursor and subsequent nodes
*/
private int leftType = 0;
private int rightType = 0;
public Student(int id, String name) {
this.id = id;
this.name = name;
}
public int getId() {
return id;
}
public void setId(int id) {
this.id = id;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public Student getLeft() {
return left;
}
public void setLeft(Student left) {
this.left = left;
}
public Student getRight() {
return right;
}
public void setRight(Student right) {
this.right = right;
}
public int getLeftType() {
return leftType;
}
public void setLeftType(int leftType) {
this.leftType = leftType;
}
public int getRightType() {
return rightType;
}
public void setRightType(int rightType) {
this.rightType = rightType;
}
@Override
public String toString() {
return "Student{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
}
Run result:
The precursor and successor nodes of the fifth node
Student{id=2, name='3'}
Student{id=1, name='1'}
Traversing Threaded Binary Trees
Student{id=4, name='8'}
Student{id=2, name='3'}
Student{id=5, name='10'}
Student{id=1, name='1'}
Student{id=6, name='14'}
Student{id=3, name='6'}
2. Application of Trees
Heap Sorting
huffman tree
Basic Introduction
- Given n n n n n n n n weight values as n leaf nodes, a binary tree is constructed. If the weighted path length (wpl) of the tree reaches the minimum, such a binary tree is called the optimal binary tree, also known as Huffman Tree.
- Huffman tree is the shortest tree with weighted path length, and nodes with larger weights are closer to the root.
Important concepts
- Path and path length: In a tree, the path between child or grandchild nodes that can be reached from one node down is called a path. The number of branches in a path is called the path length. If the number of layers of the root node is specified as 1, the path length from the root node to the layer L node is L-1
- Node weight and weighted path length: If a node in a tree is assigned a value with some meaning, this value is called the node weight
- The weighted path length of a node is the product of the path length from the root node to the node and the weight of the node (W × L)
- Weighted path length of a tree: The weighted path length of a tree is specified as the sum of the weighted path lengths of all leaf nodes (W1) × L1+W2 × L2...), denoted as WPL (weighted path length), the binary tree with larger weight nearer to the root node is the optimal binary tree.
- The smallest WPL is the Huffman tree
Create ideas and illustrations
Create ideas
- Sort from smallest to largest, each data is a node, each node can be seen as the simplest binary tree
- Remove the two binary trees with the smallest root node weight
- Makes up a new binary tree whose root node weights are the sum of the first two binary tree root nodes
- Then reorder the new binary tree with the weight size of the root node and repeat the steps 1-2-3-4 until all the data in the sequence is processed to get a Huffman tree
graphic
Take {3, 6, 7, 1, 8, 29, 13} for example
Sort first: {1, 3, 6, 7, 8, 13, 29}
Huffman tree code implementation:
public class HuffmanTree {
public static void main(String[] args) {
int arr[] = {13,7,8,3,29,6,1};
Node node = createHuffmanTree(arr);
preOrder(node);
}
public static void preOrder(Node node) {
if (node != null) {
node.preOrder();
} else {
System.out.println("Is an empty tree,Cannot traverse");
}
}
/**
* Method of creating a Huffman tree
* @param arr An array that needs to be created as a Huffman tree
* @return root node of the created Huffman tree
*/
public static Node createHuffmanTree(int[] arr) {
//Traversing through the arrarrarray makes each arr element a Node and places it in the ArrayList
ArrayList<Node> nodes = new ArrayList<>();
for (int value : arr) {
nodes.add(new Node(value));
}
while (nodes.size() > 1) {
//Sort from smallest to largest
Collections.sort(nodes);
System.out.println("nodes: = "+nodes);
//Remove the two binary trees with the smallest root node weight
//1. Remove the node with the smallest weight (binary tree)
Node leftNode = nodes.get(0);
//2. Remove the second smallest weight node (binary tree)
Node rightNode = nodes.get(1);
//3. Build a new binary tree
Node parent = new Node(leftNode.value + rightNode.value);
parent.left = leftNode;
parent.right = rightNode;
//4. Delete processed binary trees from ArrayList
nodes.remove(leftNode);
nodes.remove(rightNode);
//5. Add parent to nodes
nodes.add(parent);
}
//Returns the root node of a Huffman tree
return nodes.get(0);
}
}
//Create Node Class
//To keep Node objects sorted Collections collection sorting
//Let Node implement the Comparable interface
class Node implements Comparable<Node> {
int value;//Node weight
Node left;//Point to left child node
Node right;//Point to right child node
//Pre-order traversal
public void preOrder() {
System.out.print(this.value + " ");
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
@Override
public int compareTo(Node o) {
//Represents sorting from smallest to largest
return this.value - o.value;
}
}
Run result:
nodes: = [Node{value=1}, Node{value=3}, Node{value=6}, Node{value=7}, Node{value=8}, Node{value=13}, Node{value=29}]
nodes: = [Node{value=4}, Node{value=6}, Node{value=7}, Node{value=8}, Node{value=13}, Node{value=29}]
nodes: = [Node{value=7}, Node{value=8}, Node{value=10}, Node{value=13}, Node{value=29}]
nodes: = [Node{value=10}, Node{value=13}, Node{value=15}, Node{value=29}]
nodes: = [Node{value=15}, Node{value=23}, Node{value=29}]
nodes: = [Node{value=29}, Node{value=38}]
67 29 38 15 7 8 23 10 4 1 3 6 13
Process finished with exit code 0
Huffman encoding
Principle and illustration
Prefix encoding: The encoding of any character will not be the prefix of any other character
- Counts the number of occurrences of each character in a string to be encoded, such as helloworld
- h:1 e:1 w:1 r:1 d:1 o:2 l:3
- The number of occurrences of a character is used as a weight to construct a Haffman tree. As follows
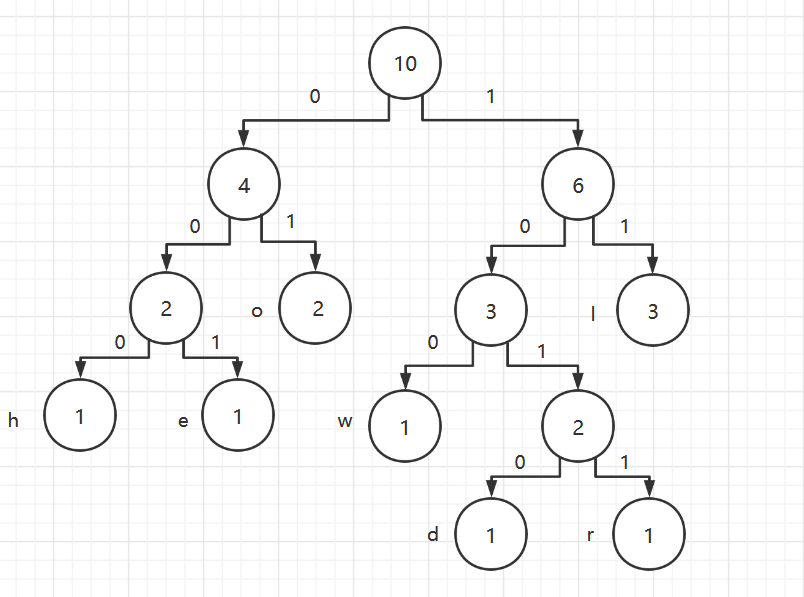
- Encoding according to the Haffman tree, the left path is 0 and the right path is 1
- The result of character encoding is: h:000 e:001 w:100 d:1010 r:1011 l:11 o:01
- The result of string encoding is: 000001111100011011011111010
Data decompression (decoding using Huffman encoding)
- The Huffman code and corresponding code byte[], i.e. [-88, -65, -56, -65...]
- Decode using Huffman encoding to get the original string
Implementation Code
This code only implements the creation of a Haffman tree and the encoding of each character
public class HuffmanCode {
public static void main(String[] args) {
String content = "i like like like java do you like a java";
final byte[] contentBytes = content.getBytes();
System.out.println(contentBytes.length);//40
List<Node> nodes = getNodes(contentBytes);
System.out.println(nodes);
//Created Binary Tree
System.out.println("huffman tree");
Node heffmanTreeRoot = creatHuffmanTree(nodes);
preOrder(heffmanTreeRoot);
//Corresponding Huffman codes
//getCodes(heffmanTreeRoot, "", stringBuilder);
Map<Byte, String> codes = getCodes(heffmanTreeRoot);
System.out.println("Generated Huffman Encoding Table:"+codes);
byte[] huffmanCodeBytes = zip(contentBytes, huffmanCodes);
System.out.println("huffmanCodeBytes"+Arrays.toString(huffmanCodeBytes));//17
//Decode
byte[] sourceBytes = decode(huffmanCodes, huffmanCodeBytes);
System.out.println("Original string:"+new String(sourceBytes));
}
//Complete data decompression
// 1. Put huffmanCodeBytes [-88, -65, -56, -65, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]
// Override the string "1010100010111..." that first converts to the corresponding binary Huffman encoding
// 2. The corresponding binary string "1010100010111..." => Contrast Huffman encoding=>"i like like like Java do you like a java"
private static byte[] decode(Map<Byte,String> huffmanCodes, byte[] huffmanBytes) {
//1. First get the binary string corresponding to Huffman Bytes in the form of 101010010111...
StringBuilder stringBuilder = new StringBuilder();
//Converts a byte array to a binary string
for (int i = 0; i < huffmanBytes.length; i++) {
byte b = huffmanBytes[i];
//Determine if it is the last byte
boolean flag = (i == huffmanBytes.length - 1);
stringBuilder.append(byteToBitString(!flag, b));
}
System.out.println("Binary string corresponding to the decoded Huffman byte array:" + stringBuilder.toString());
//Decodes a string according to the specified Huffman encoding
//Convert the Huffman coding table because the reverse query is a->100->a
HashMap<String, Byte> map = new HashMap<>();
for (Map.Entry<Byte, String> entry: huffmanCodes.entrySet()) {
map.put(entry.getValue(), entry.getKey());
}
System.out.println("reverse map="+ map);
//Create a collection to hold byte s
ArrayList<Byte> list = new ArrayList<>();
//i Index Scan stringBuilder
for (int i = 0; i < stringBuilder.length(); ) {
int count = 1;//Small counters
boolean flag = true;
Byte b = null;
while (flag) {
//Incrementally remove'1''0'
String key = stringBuilder.substring(i, i + count); //i Fixed, let count move, specify a match to a character
b = map.get(key);
if (b == null) {//Description does not match
count++;
} else {
//Match to
flag = false;
}
}
list.add(b);
i += count;//i Move directly to count
}
//The data in the list is placed in byte[] and returned
byte b[] = new byte[list.size()];
for (int i = 0; i < b.length; i++) {
b[i] = list.get(i);
}
return b;
}
/**
* Convert a byte to a binary string
* @param flag Flag need to be filled-in if true, indicates need to be filled-in, false does not need to be filled-in
* @param b Incoming byte
* @return Is the binary string for that b (note that it is returned by complement)
*/
private static String byteToBitString(boolean flag, byte b) {
//Save b with a variable
int temp = b;//Convert b to int
//If it's a positive number, we still have a filling position
if (flag) {
temp |= 256; //Bitwise or 256 1 0000 0000 | 0000 0001 => 1 0000 0001
}
String str = Integer.toBinaryString(temp);//Returns the complement of the binary corresponding to temp
if (flag) {
return str.substring(str.length() - 8);
} else {
return str;
}
}
/**
* Write a method that returns a compressed byte[] with a generated Huffman encoding table from an array of bytes[] corresponding to the string
* @param bytes byte[] corresponding to the original string
* @param huffmanCodes Generated Huffman coded map
* @return
*/
private static byte[] zip(byte[] bytes, Map<Byte,String> huffmanCodes) {
//1. Use huffmanCodes to convert byte to a string corresponding to Huffman encoding
StringBuilder stringBuilder = new StringBuilder();
//Traversing byte arrays
for (byte b: bytes) {
stringBuilder.append(huffmanCodes.get(b));
}
//Will "10101000101111111110..." Convert to byte[]
//Statistics return byte[] huffmanCodeBytes length
int len;
if (stringBuilder.length() % 8 == 0) {
len = stringBuilder.length() / 8;
} else {
len = stringBuilder.length() / 8 + 1;
}
//Create a compressed byte array for storage
byte[] huffmanCodeBytes = new byte[len];
int index = 0;//Record is the first byte
for (int i = 0; i < stringBuilder.length(); i += 8) {//Because each 8 bits corresponds to a byte, step+8
String strByte;
if (i+8 > stringBuilder.length()) {
//Not enough 8 bits
strByte = stringBuilder.substring(i);
} else {
strByte = stringBuilder.substring(i, i+8);
}
//Convert strByte to a byte and place it in Huffman CopyBytes
huffmanCodeBytes[index] = (byte)Integer.parseInt(strByte, 2);
index++;
}
return huffmanCodeBytes;
}
//Generating codes corresponding to a Huffman tree
//1. Store the Huffman coding table in the form of Map<Byte,String>
// 32 ->01 97 -> 100 100 -> 11000
static Map<Byte,String> huffmanCodes = new HashMap<>();
//2 Regenerating a Huffman code indicates that a path needs to be unjoined to define a StringBuilder path to store a leaf node
static StringBuilder stringBuilder = new StringBuilder();
//For easy invocation
private static Map<Byte,String> getCodes(Node root) {
if (root == null) {
return null;
}
getCodes(root, "", stringBuilder);
return huffmanCodes;
}
/**
* Gets the Huffman codes of all leaf nodes of the incoming Node node and puts them into the huffmanCode collection
* @param node Incoming Node
* @param code Path left node is 0 Node 1
* @param stringBuilder For stitching paths
*/
private static void getCodes(Node node, String code, StringBuilder stringBuilder) {
StringBuilder stringBuilder2 = new StringBuilder(stringBuilder);
//Add code to stringBuilder2
stringBuilder2.append(code);
if (node != null) {
//Determine whether the current node is a leaf node or a non-leaf node
if (node.data == null) {//Nonleaf Nodes
//Left Recursive Processing
getCodes(node.left, "0", stringBuilder2);
//Recursion Right
getCodes(node.right, "1", stringBuilder2);
} else {
//That means the leaf node is the last one to find a leaf node
huffmanCodes.put(node.data, stringBuilder2.toString());
}
}
}
//Pre-order traversal
private static void preOrder(Node root) {
if (root != null) {
root.preOrder();
} else {
System.out.println("The Huffman tree is empty");
}
}
/**
*
* @param bytes Receive byte array
* @return Return is List
*/
private static List<Node> getNodes(byte[] bytes) {
//1. Create an ArrayList
ArrayList<Node> nodes = new ArrayList<>();
//2. Traverse bytes and count the number of occurrences of each byte - >map[key, value]
HashMap<Byte, Integer> map = new HashMap<>();
for (byte b : bytes) {
Integer count = map.get(b);
if (count == null) {
map.put(b, 1);
} else {
map.put(b, count + 1);
}
}
//Turn each key-value pair into a Node object and add it to the nodes collection
//Traversing a map
for (Map.Entry<Byte, Integer> entry : map.entrySet()) {
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
//Create a corresponding Huffman tree from a List
private static Node creatHuffmanTree (List<Node> nodes) {
while (nodes.size() > 1) {
//Sort from smallest to largest
Collections.sort(nodes);
//Take out the first smallest binary tree
Node leftNode = nodes.get(0);
//Take out the second smallest binary tree
Node rightNode = nodes.get(1);
//Create a new binary tree whose root node has no data and only weights
Node parent = new Node(null, leftNode.weight + rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
//Remove the two binary trees processed from the nodes
nodes.remove(leftNode);
nodes.remove(rightNode);
//Add a new binary tree to nodes
nodes.add(parent);
}
//The last node of nodes is the root node of the Huffman tree
return nodes.get(0);
}
}
class Node implements Comparable<Node>{
Byte data; //Store data (character itself), e.g.'a'=> 97
int weight; //Weight, indicating the number of occurrences of a character
Node left;
Node right;
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
//Sort from smallest to largest
return this.weight - o.weight;
}
@Override
public String toString() {
return "Node{" +
"data=" + data +
", weight=" + weight +
'}';
}
//Pre-order traversal
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
}
Run result:
40
[Node{data=32, weight=9}, Node{data=97, weight=5}, Node{data=100, weight=1}, Node{data=101, weight=4}, Node{data=117, weight=1}, Node{data=118, weight=2}, Node{data=105, weight=5}, Node{data=121, weight=1}, Node{data=106, weight=2}, Node{data=107, weight=4}, Node{data=108, weight=4}, Node{data=111, weight=2}]
huffman tree
Node{data=null, weight=40}
Node{data=null, weight=17}
Node{data=null, weight=8}
Node{data=108, weight=4}
Node{data=null, weight=4}
Node{data=106, weight=2}
Node{data=111, weight=2}
Node{data=32, weight=9}
Node{data=null, weight=23}
Node{data=null, weight=10}
Node{data=97, weight=5}
Node{data=105, weight=5}
Node{data=null, weight=13}
Node{data=null, weight=5}
Node{data=null, weight=2}
Node{data=100, weight=1}
Node{data=117, weight=1}
Node{data=null, weight=3}
Node{data=121, weight=1}
Node{data=118, weight=2}
Node{data=null, weight=8}
Node{data=101, weight=4}
Node{data=107, weight=4}
Generated Huffman Encoding Table:{32=01, 97=100, 100=11000, 117=11001, 101=1110, 118=11011, 105=101, 121=11010, 106=0010, 107=1111, 108=000, 111=0011}
huffmanCodeBytes[-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]
Binary string corresponding to the decoded Huffman byte array:1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100
reverse map={000=108, 01=32, 100=97, 101=105, 11010=121, 0011=111, 1111=107, 11001=117, 1110=101, 11000=100, 11011=118, 0010=106}
Original string:i like like like java do you like a java
Process finished with exit code 0
File Compression Decompression
Compression: Read file - > Get Huffman encoding table - > Complete compression
Decompression: Read compressed files (data and Huffman encoding table) ->Complete decompression (file recovery)
public class HuffmanCodeWenjian {
public static void main(String[] args) {
//Test Compressed File
//String srcFile = "E://123.txt";
//String dstFile = "E://dst.zip";
//zipFile(srcFile, dstFile);
//System.out.println("compressed file ok");
//Test decompression file
String zipFile = "E://dst.zip";
String dstFile = "E://1232.txt";
unZipFiles(zipFile, dstFile);
System.out.println("Successful decompression");
}
//Write method to complete decompression of compressed files
/**
*
* @param zipFile Incoming Compressed File Path
* @param dstFile Path to unzip the file
*/
public static void unZipFiles(String zipFile, String dstFile) {
//Define File Input Stream
InputStream is = null;
//Define an object input stream
ObjectInputStream ois = null;
//Define File Output Stream
OutputStream os = null;
try {
//Create File Input Stream
is = new FileInputStream(zipFile);
//Create an object input stream associated with is
ois = new ObjectInputStream(is);
//Read byte array huffmanBytes
byte[] huffmanBytes =(byte[]) ois.readObject();
//Read the Huffman Encoding Table
Map<Byte, String> huffmanCodes = (Map<Byte, String>) ois.readObject();
//Decode
byte[] bytes = decode(huffmanCodes, huffmanBytes);
//Write bytes array to target file
os = new FileOutputStream(dstFile);
//Write data to dstFile file
os.write(bytes);
} catch (Exception e) {
System.out.println(e.getMessage());
} finally {
try {
os.close();
ois.close();
is.close();
} catch (Exception e) {
System.out.println(e.getMessage());
}
}
}
//Writing method compresses a file
/**
*
* @param srcFile Full path to incoming compressed file
* @param dstFile Compressed directory
*/
public static void zipFile(String srcFile, String dstFile) {
//Create Output Stream of File
FileOutputStream os = null;
ObjectOutputStream oos = null;
//Create input stream for file
FileInputStream is = null;
try {
//Create input stream for file
is = new FileInputStream(srcFile);
//Create a byte of the same size as the source file[]
byte[] b = new byte[is.available()];
//read file
is.read(b);
//Direct compression of source files
byte[] huffmanBytes = huffmanZip(b);
//Create an output stream of files to hold compressed files
os = new FileOutputStream(dstFile);
//Create an ObjectOutputStream associated with the file output stream
oos = new ObjectOutputStream(os);
//Write a Huffman encoded byte array to a compressed file
oos.writeObject(huffmanBytes);
//This is where the Huffman encoding is written as an object stream, which is used to recover the source files
//Be sure to write the Huffman encoding to a compressed file
oos.writeObject(huffmanCodes);
} catch (Exception e) {
System.out.println(e.getMessage());
} finally {
try {
is.close();
oos.close();
os.close();
} catch (Exception e) {
System.out.println(e.getMessage());
}
}
}
//Complete data decompression
// 1. Put huffmanCodeBytes [-88, -65, -56, -65, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]
// Override the string "1010100010111..." that first converts to the corresponding binary Huffman encoding
// 2. The corresponding binary string "1010100010111..." => Contrast Huffman encoding=>"i like like like Java do you like a java"
private static byte[] decode(Map<Byte,String> huffmanCodes, byte[] huffmanBytes) {
//1. First get the binary string corresponding to Huffman Bytes in the form of 101010010111...
StringBuilder stringBuilder = new StringBuilder();
//Converts a byte array to a binary string
for (int i = 0; i < huffmanBytes.length; i++) {
byte b = huffmanBytes[i];
//Determine if it is the last byte
boolean flag = (i == huffmanBytes.length - 1);
stringBuilder.append(byteToBitString(!flag, b));
}
System.out.println("Binary string corresponding to the decoded Huffman byte array:" + stringBuilder.toString());
//Decodes a string according to the specified Huffman encoding
//Convert the Huffman coding table because the reverse query is a->100->a
HashMap<String, Byte> map = new HashMap<>();
for (Map.Entry<Byte, String> entry: huffmanCodes.entrySet()) {
map.put(entry.getValue(), entry.getKey());
}
System.out.println("reverse map="+ map);
//Create a collection to hold byte s
ArrayList<Byte> list = new ArrayList<>();
//i Index Scan stringBuilder
for (int i = 0; i < stringBuilder.length(); ) {
int count = 1;//Small counters
boolean flag = true;
Byte b = null;
while (flag) {
//Incrementally remove'1''0'
String key = stringBuilder.substring(i, i + count); //i Fixed, let count move, specify a match to a character
b = map.get(key);
if (b == null) {//Description does not match
count++;
} else {
//Match to
flag = false;
}
}
list.add(b);
i += count;//i Move directly to count
}
//The data in the list is placed in byte[] and returned
byte b[] = new byte[list.size()];
for (int i = 0; i < b.length; i++) {
b[i] = list.get(i);
}
return b;
}
/**
* Encapsulate into a method
* @param bytes The byte array corresponding to the original string
* @return
*/
private static byte[] huffmanZip(byte[] bytes) {
List<Node> nodes = getNodes(bytes);
//Creating a Huffman Tree from nodes
Node heffmanTreeRoot = creatHuffmanTree(nodes);
//Generate corresponding Huffman codes
Map<Byte, String> codes = getCodes(heffmanTreeRoot);
//Compressed Huffman encoded byte array based on the generated Huffman encoding
byte[] huffmanCodeBytes = zip(bytes, huffmanCodes);
return huffmanCodeBytes;
}
/**
* Convert a byte to a binary string
* @param flag Flag need to be filled-in if true, indicates need to be filled-in, false does not need to be filled-in
* @param b Incoming byte
* @return Is the binary string for that b (note that it is returned by complement)
*/
private static String byteToBitString(boolean flag, byte b) {
//Save b with a variable
int temp = b;//Convert b to int
//If it's a positive number, we still have a filling position
if (flag) {
temp |= 256; //Bitwise or 256 1 0000 0000 | 0000 0001 => 1 0000 0001
}
String str = Integer.toBinaryString(temp);//Returns the complement of the binary corresponding to temp
if (flag) {
return str.substring(str.length() - 8);
} else {
return str;
}
}
/**
* Write a method that returns a compressed byte[] with a generated Huffman encoding table from an array of bytes[] corresponding to the string
* @param bytes byte[] corresponding to the original string
* @param huffmanCodes Generated Huffman coded map
* @return
*/
private static byte[] zip(byte[] bytes, Map<Byte,String> huffmanCodes) {
//1. Use huffmanCodes to convert byte to a string corresponding to Huffman encoding
StringBuilder stringBuilder = new StringBuilder();
//Traversing byte arrays
for (byte b: bytes) {
stringBuilder.append(huffmanCodes.get(b));
}
//Will "10101000101111111110..." Convert to byte[]
//Statistics return byte[] huffmanCodeBytes length
int len;
if (stringBuilder.length() % 8 == 0) {
len = stringBuilder.length() / 8;
} else {
len = stringBuilder.length() / 8 + 1;
}
//Create a compressed byte array for storage
byte[] huffmanCodeBytes = new byte[len];
int index = 0;//Record is the first byte
for (int i = 0; i < stringBuilder.length(); i += 8) {//Because each 8 bits corresponds to a byte, step+8
String strByte;
if (i+8 > stringBuilder.length()) {
//Not enough 8 bits
strByte = stringBuilder.substring(i);
} else {
strByte = stringBuilder.substring(i, i+8);
}
//Convert strByte to a byte and place it in Huffman CopyBytes
huffmanCodeBytes[index] = (byte)Integer.parseInt(strByte, 2);
index++;
}
return huffmanCodeBytes;
}
//Generating codes corresponding to a Huffman tree
//1. Store the Huffman coding table in the form of Map<Byte,String>
// 32 ->01 97 -> 100 100 -> 11000
static Map<Byte,String> huffmanCodes = new HashMap<>();
//2 Regenerating a Huffman code indicates that a path needs to be unjoined to define a StringBuilder path to store a leaf node
static StringBuilder stringBuilder = new StringBuilder();
//For easy invocation
private static Map<Byte,String> getCodes(Node root) {
if (root == null) {
return null;
}
getCodes(root, "", stringBuilder);
return huffmanCodes;
}
/**
* Gets the Huffman codes of all leaf nodes of the incoming Node node and puts them into the huffmanCode collection
* @param node Incoming Node
* @param code Path left node is 0 Node 1
* @param stringBuilder For stitching paths
*/
private static void getCodes(Node node, String code, StringBuilder stringBuilder) {
StringBuilder stringBuilder2 = new StringBuilder(stringBuilder);
//Add code to stringBuilder2
stringBuilder2.append(code);
if (node != null) {
//Determine whether the current node is a leaf node or a non-leaf node
if (node.data == null) {//Nonleaf Nodes
//Left Recursive Processing
getCodes(node.left, "0", stringBuilder2);
//Recursion Right
getCodes(node.right, "1", stringBuilder2);
} else {
//That means the leaf node is the last one to find a leaf node
huffmanCodes.put(node.data, stringBuilder2.toString());
}
}
}
//Pre-order traversal
private static void preOrder(Node root) {
if (root != null) {
root.preOrder();
} else {
System.out.println("The Huffman tree is empty");
}
}
/**
*
* @param bytes Receive byte array
* @return Return is List
*/
private static List<Node> getNodes(byte[] bytes) {
//1. Create an ArrayList
ArrayList<Node> nodes = new ArrayList<>();
//2. Traverse bytes and count the number of occurrences of each byte - >map[key, value]
HashMap<Byte, Integer> map = new HashMap<>();
for (byte b : bytes) {
Integer count = map.get(b);
if (count == null) {
map.put(b, 1);
} else {
map.put(b, count + 1);
}
}
//Turn each key-value pair into a Node object and add it to the nodes collection
//Traversing a map
for (Map.Entry<Byte, Integer> entry : map.entrySet()) {
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
//Create a corresponding Huffman tree from a List
private static Node creatHuffmanTree (List<Node> nodes) {
while (nodes.size() > 1) {
//Sort from smallest to largest
Collections.sort(nodes);
//Take out the first smallest binary tree
Node leftNode = nodes.get(0);
//Take out the second smallest binary tree
Node rightNode = nodes.get(1);
//Create a new binary tree whose root node has no data and only weights
Node parent = new Node(null, leftNode.weight + rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
//Remove the two binary trees processed from the nodes
nodes.remove(leftNode);
nodes.remove(rightNode);
//Add a new binary tree to nodes
nodes.add(parent);
}
//The last node of nodes is the root node of the Huffman tree
return nodes.get(0);
}
}
class Node implements Comparable<Node>{
Byte data; //Store data (character itself), e.g.'a'=> 97
int weight; //Weight, indicating the number of occurrences of a character
Node left;
Node right;
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
//Sort from smallest to largest
return this.weight - o.weight;
}
@Override
public String toString() {
return "Node{" +
"data=" + data +
", weight=" + weight +
'}';
}
//Pre-order traversal
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
}
Binary Sort Tree
Basic Introduction
Binary Sort Tree: BST: (Binary Sort(Search) Tree), for any non-leaf node of a binary sort tree, the value of the left child node is required to be smaller than that of the current node, and the value of the right child node is greater than that of the current node.
- Specifically: if the same value exists, the node can be placed in a left or right child node
For example, for the previous data (7, 3, 10, 12, 5, 1, 9), the corresponding binary sort tree is:
Operational ideas
Add to
- Find the location where a node should be inserted based on its value
- All newly inserted nodes are leaf nodes
delete
Delete leaf nodes (e.g. delete values of 2 nodes)
- Find Node to Delete
- Find the parent of the node to be deleted
- Determine if the node to be deleted is the left or right child of its parent and leave it empty
Delete a node that has only one subtree (for example, delete a node with a value of 1)
-
Find the node targetNode to be deleted
-
Find parent node of targetNode to delete
-
Determines whether the child node of targetNode is a left or right child node
-
Is targetNode a parent's left or right child node
-
If targetNode is a left child node
-
If targetNode is the left child node of parent
parent.left = targetNode.left
-
If targetNode is the right child node of parent
parent.right = targetNode.left
-
-
If targetNode is a right child node
-
If targetNode is the left child node of parent
parent.left = targetNode.right
-
If targetNode is the right child node of parent
parent.right = targetNode.right
-
Delete nodes with two subtrees (such as nodes with a deletion value of 10)
- Find the node targetNode to be deleted
- Find parent node of targetNode
- Find the smallest node from the right subtree of targetNode
- Save the minimum node value temp = 12 with a temporary variable
- Delete the smallest node
- targetNode.value = temp
Delete the root node (such as a node with a value of 7)
- The method of deleting the root node is similar to that of deleting two subtrees
- Find a node close to the root node value
- Delete the node and assign its value to the root node
Code:
public class BinarySortTreeDemo {
public static void main(String[] args) {
int[] arr = {7,3,10,12,5,1,9};
BinarySortTree binarySortTree = new BinarySortTree();
//Loop Add Node to Binary Sort Tree
for (int i = 0; i < arr.length; i++) {
binarySortTree.add(new Node(arr[i]));
}
//Medium Order Traversal Binary Sort Tree
System.out.println("Medium Order Traversal Binary Sort Tree");
binarySortTree.infixOrder();
//Delete leaf nodes
//binarySortTree.delNode(5);
binarySortTree.delNode(7);
System.out.println("After deleting a node");
binarySortTree.infixOrder();
}
}
//Create Binary Sort Tree
class BinarySortTree {
private Node root;
//Find Nodes to Delete
public Node search(int value) {
if (root == null) {
return null;
} else {
return root.search(value);
}
}
//Find the parent node to delete
public Node searchParent(int value) {
if (root == null) {
return null;
} else {
return root.searchParent(value);
}
}
//Write a method
//1. The value returned for the smallest node of a binary ordered tree with a node as its root
//2. Delete the smallest node of a binary sorted tree where node is the root node
/**
*
* @param node Incoming node (as the root node of a binary sorted tree)
* @return Returns the value of the smallest node of a binary ordered tree with node as its root node
*/
public int delRightTreeMin(Node node) {
Node target = node;
//Loop to find the left node, and you will find the minimum
while (target.left != null) {
target = target.left;
}
//The target then points to the smallest node
//Delete the smallest node
delNode(target.value);
return target.value;
}
//Delete Node
public void delNode(int value) {
if (root == null) {
return;
} else {
//1. Find the node targetNode to delete first
Node targetNode = search(value);
//If no node was found to delete
if (targetNode == null) {
return;
}
//If we find that the current binary sorting tree has only one node
if (root.left == null && root.right == null) {
root = null;
return;
}
//To find the parent node of targetNode
Node parent = searchParent(value);
//If the node to be deleted is a leaf node
if (targetNode.left == null && targetNode.right == null) {
//Determines whether the targetNode is the left or right child of the parent node
if (parent.left != null && parent.left.value == value) {//Is a left child node
parent.left = null;
} else if (parent.right != null && parent.right.value == value) {//Is the right child node
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) {//Delete nodes with two subtrees
int minVal = delRightTreeMin(targetNode.right);
targetNode.value = minVal;
} else {//Delete nodes with only one subtree
//If the node to be deleted has left child nodes
if (targetNode.left != null) {
if (parent != null) {
//If targetNode is the left child node of parent
if (parent.left.value == value) {
parent.left = targetNode.left;
} else {//targetNode is the right child node of parent
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else {
//The node to be deleted has right child nodes
if (parent != null) {
//If targetNode is the left child node of parent
if (parent.left.value == value) {
parent.left = targetNode.right;
} else {//targetNode is the right child node of parent
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
//Method of adding nodes
public void add(Node node) {
if (root == null) {
//If the root is empty, direct the root to the node
root = node;
} else {
root.add(node);
}
}
//Intermediate traversal
public void infixOrder() {
if (root != null) {
root.infixOrder();
} else {
System.out.println("Binary sort tree is empty,Cannot traverse");
}
}
}
//Create node
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
//Find Nodes to Delete
/**
*
* @param value The value of the node you want to delete
* @return Return null if found
*/
public Node search(int value) {
if (value == this.value) {
//Find is the node
return this;
} else if (value < this.value) {//If the value found is less than the current node, recursively look to the left subtree
//If left child node is empty
if (this.left == null) {
return null;
}
return this.left.search(value);
} else {//If the value found is not less than the current node, recursively look to the right subtree
if (this.right == null) {
return null;
}
return this.right.search(value);
}
}
//Find parent node to delete node
/**
*
* @param value Value of the node to be found
* @return Returns the parent node of the node to be deleted, or null if not
*/
public Node searchParent(int value) {
//Return if the current node is the parent of the node to be deleted
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else {
//If the value found is less than the value of the current node and the left child node of the current node is not empty
if (value < this.value && this.left != null) {
return this.left.searchParent(value);//Recursive search to left subtree
} else if (value >= this.value && this.right != null) {
return this.right.searchParent(value);
} else {
return null;//Parent node not found
}
}
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
//Method of adding nodes
//Add nodes recursively, noting that you need to satisfy the requirements of a binary sort tree
public void add(Node node) {
if (node == null) {
return;
}
//Determine the value relationship between the incoming node and the root node of the current subtree
if (node.value < this.value) {
//If the left child of the current node is null
if (this.left == null) {
this.left = node;
} else {
//Recursively add to left subtree
this.left.add(node);
}
} else {//The value of the added node is greater than that of the current node
if (this.right == null) {
this.right = node;
} else {
//Recursively add to right subtree
this.right.add(node);
}
}
}
//Intermediate traversal
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
}
Run result:
Medium Order Traversal Binary Sort Tree
Node{value=1}
Node{value=3}
Node{value=5}
Node{value=7}
Node{value=9}
Node{value=10}
Node{value=12}
After deleting a node
Node{value=1}
Node{value=3}
Node{value=5}
Node{value=9}
Node{value=10}
Node{value=12}
Process finished with exit code 0
Balanced Binary Tree (AVL Tree)
Basic Introduction
Why balanced binary trees are needed
- If you construct a binary sorting tree from an array {1, 2, 3, 4}, the resulting binary tree not only does not reflect its characteristics, but also degenerates into a list of chains
brief introduction
- Balanced binary tree, also known as Self-balancing binary search tree, is also known as AVL tree, which guarantees high query efficiency.
- It has the following characteristics:
- It is an empty tree or its left and right subtrees have absolute height differences of no more than 1, and both subtrees are balanced binary trees
- Common implementation methods of balanced binary tree are red-black tree, AVL, scapegoat tree, Treap, stretch tree, etc.
- The binary tree shown in the following figure is a balanced binary tree
Application Case - Left Rotation
Modify the binary sorting tree constructed by the column {4,3,6,5,7,8} to a balanced binary tree
Here the right subtree is higher than the left subtree, and the difference is greater than 1, so you need to rotate it to the left to reduce the height of the right subtree
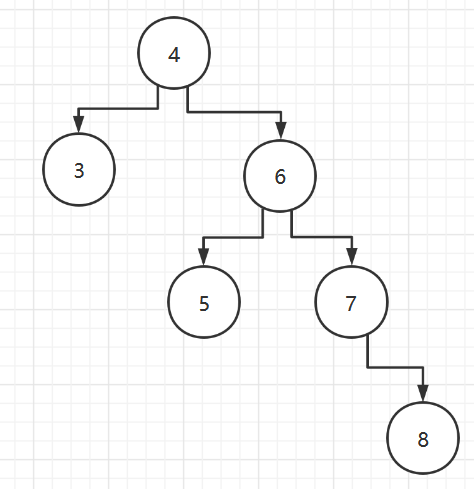
step
- Create a new node, newNode, with the value of the current node (4), equal to the value of the current root node
-
Set the left subtree of the new node to the left subtree of the current node
newNode.left = left
-
Set the right subtree of the new node to the left subtree of the right subtree of the current node
newNode.right = right.left
-
Change the value of the current node to the value of its right subtree
value = right.value
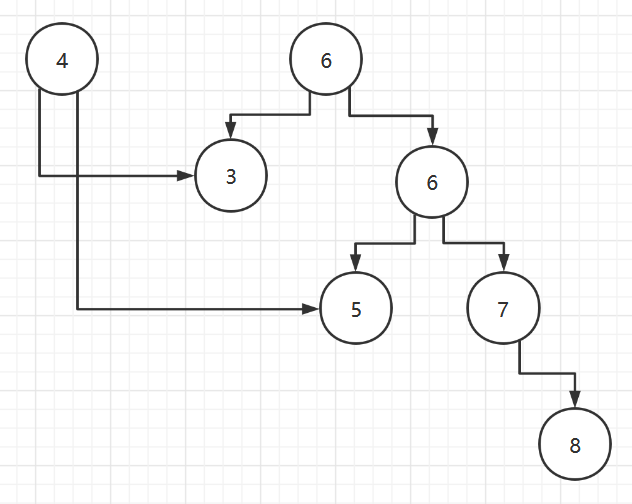
-
Change the right subtree of the current node to the right subtree of its right subtree
right = right.right
-
Point the current node's left subtree to the new node
left = newLeft
Compiled results
Application Case - Right Rotation
When the left subtree height of a binary sorted tree is greater than the right subtree height and the difference is greater than 1, a right rotation is needed to reduce the left subtree height.
step
- Create a new node whose value is the value of the current node
- Point the right subtree of the new node to the right subtree of the current node
- Point the left subtree of the new node to the right subtree of the left subtree of the current node
- Change the value of the current node to the value of its left subtree
- Point the left subtree of the current node to the left subtree of its left subtree
- Point the right subtree of the current node to the new node
Application Case - Double Rotation
Sometimes just rotating left or right does not turn a binary sorting tree into a balanced binary tree. This requires double rotation, that is, both left and right rotation.
- When rotating left, if the left subtree of the current node's right subtree is higher than its right subtree, the right node of the current node needs to be rotated right, and then the current node needs to be rotated right-left
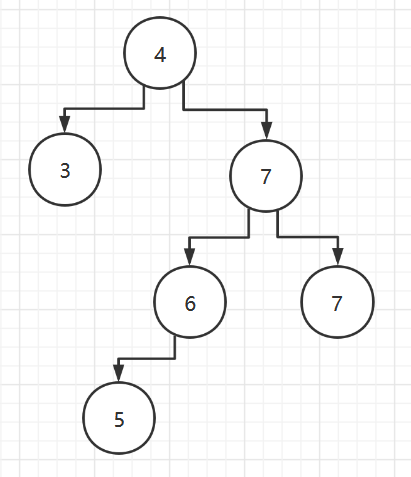
- When rotating right, if the right subtree of the current node's left subtree is higher than the left subtree of its left subtree, the left node of the current node needs to be rotated left, and then the current node needs to be rotated right
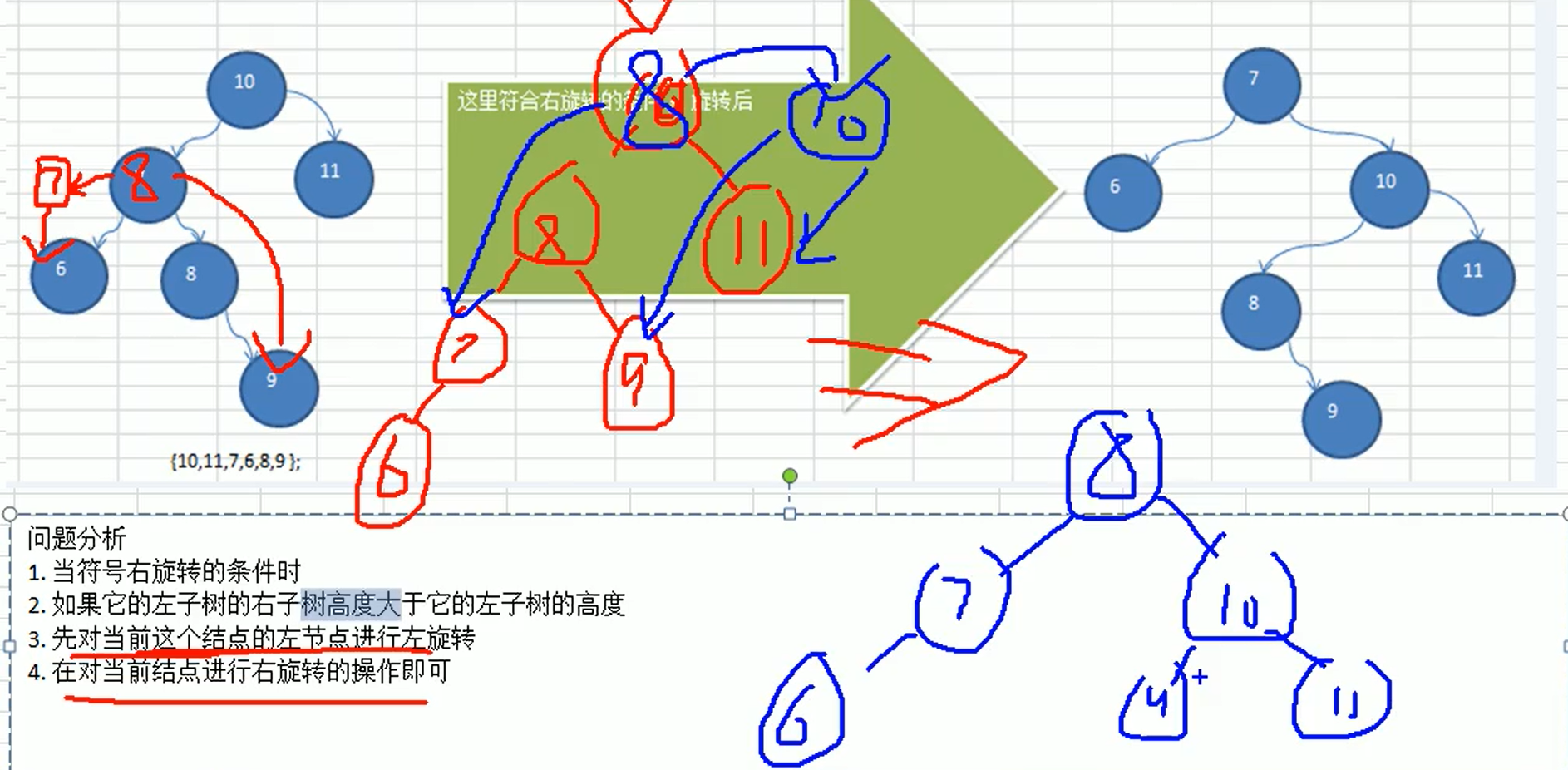
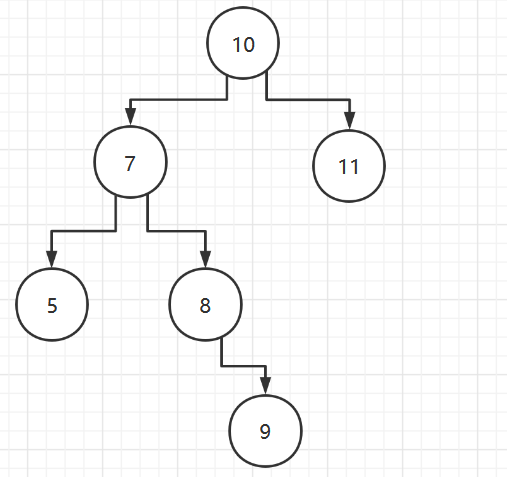
Implementation Code
public class AVLTreeDemo {
public static void main(String[] args) {
//int[] arr = {4,3,6,5,7,8};
//int[] arr = {10,12,8,9,7,6};
int[] arr = {10,11,7,6,8,9};
//Create an AVLTree
AVLTree avlTree = new AVLTree();
//Add Node
for (int i = 0; i < arr.length; i++) {
avlTree.add(new Node(arr[i]));
}
System.out.println("Intermediate traversal");
avlTree.infixOrder();
System.out.println("Before unbalanced processing~~~");
System.out.println("Tree Height:" + avlTree.getRoot().height());
System.out.println("Height of the left subtree:" + avlTree.getRoot().leftHeight());
System.out.println("Height of right subtree:" + avlTree.getRoot().rightHeight());
System.out.println("Current Root Node:" + avlTree.getRoot());
}
}
//Create AVLTree
class AVLTree {
private Node root;
public Node getRoot() {
return root;
}
//Find Nodes to Delete
public Node search(int value) {
if (root == null) {
return null;
} else {
return root.search(value);
}
}
//Find the parent node to delete
public Node searchParent(int value) {
if (root == null) {
return null;
} else {
return root.searchParent(value);
}
}
//Write a method
//1. The value returned for the smallest node of a binary ordered tree with a node as its root
//2. Delete the smallest node of a binary sorted tree where node is the root node
/**
*
* @param node Incoming node (as the root node of a binary sorted tree)
* @return Returns the value of the smallest node of a binary ordered tree with node as its root node
*/
public int delRightTreeMin(Node node) {
Node target = node;
//Loop to find the left node, and you will find the minimum
while (target.left != null) {
target = target.left;
}
//The target then points to the smallest node
//Delete the smallest node
delNode(target.value);
return target.value;
}
//Delete Node
public void delNode(int value) {
if (root == null) {
return;
} else {
//1. Find the node targetNode to delete first
Node targetNode = search(value);
//If no node was found to delete
if (targetNode == null) {
return;
}
//If we find that the current binary sorting tree has only one node
if (root.left == null && root.right == null) {
root = null;
return;
}
//To find the parent node of targetNode
Node parent = searchParent(value);
//If the node to be deleted is a leaf node
if (targetNode.left == null && targetNode.right == null) {
//Determines whether the targetNode is the left or right child of the parent node
if (parent.left != null && parent.left.value == value) {//Is a left child node
parent.left = null;
} else if (parent.right != null && parent.right.value == value) {//Is the right child node
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) {//Delete nodes with two subtrees
int minVal = delRightTreeMin(targetNode.right);
targetNode.value = minVal;
} else {//Delete nodes with only one subtree
//If the node to be deleted has left child nodes
if (targetNode.left != null) {
if (parent != null) {
//If targetNode is the left child node of parent
if (parent.left.value == value) {
parent.left = targetNode.left;
} else {//targetNode is the right child node of parent
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else {
//The node to be deleted has right child nodes
if (parent != null) {
//If targetNode is the left child node of parent
if (parent.left.value == value) {
parent.left = targetNode.right;
} else {//targetNode is the right child node of parent
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
//Method of adding nodes
public void add(Node node) {
if (root == null) {
//If the root is empty, direct the root to the node
root = node;
} else {
root.add(node);
}
}
//Intermediate traversal
public void infixOrder() {
if (root != null) {
root.infixOrder();
} else {
System.out.println("Binary sort tree is empty,Cannot traverse");
}
}
}
//Create node
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
//Returns the height of the left subtree
public int leftHeight() {
if (left == null) {
return 0;
}
return left.height();
}
//Returns the height of the right subtree
public int rightHeight() {
if (right == null) {
return 0;
}
return right.height();
}
//Returns the height of the tree with this node as its root
public int height() {
return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}
//Left Rotation
private void leftRotate() {
//Create a new node with the current root node value
Node newNode = new Node(value);
//Set the left subtree of the new node to the left subtree of the current node
newNode.left = left;
//Set the right subtree of the new node to the left subtree of the right subtree of the current node
newNode.right = right.left;
//Change the value of the current node to the value of the right child node
value = right.value;
//Sets the right subtree of the current node to the right subtree of the current node's right subtree
right = right.right;
//Set the left subtree (left child node) of the current node to a new node
left = newNode;
}
//Right Rotation
private void rightRotate() {
Node newNode = new Node(value);
newNode.right = right;
newNode.left = left.right;
value = left.value;
left = left.left;
right = newNode;
}
//Find Nodes to Delete
/**
*
* @param value The value of the node you want to delete
* @return Return null if found
*/
public Node search(int value) {
if (value == this.value) {
//Find is the node
return this;
} else if (value < this.value) {//If the value found is less than the current node, recursively look to the left subtree
//If left child node is empty
if (this.left == null) {
return null;
}
return this.left.search(value);
} else {//If the value found is not less than the current node, recursively look to the right subtree
if (this.right == null) {
return null;
}
return this.right.search(value);
}
}
//Find parent node to delete node
/**
*
* @param value Value of the node to be found
* @return Returns the parent node of the node to be deleted, or null if not
*/
public Node searchParent(int value) {
//Return if the current node is the parent of the node to be deleted
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else {
//If the value found is less than the value of the current node and the left child node of the current node is not empty
if (value < this.value && this.left != null) {
return this.left.searchParent(value);//Recursive search to left subtree
} else if (value >= this.value && this.right != null) {
return this.right.searchParent(value);
} else {
return null;//Parent node not found
}
}
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
//Method of adding nodes
//Add nodes recursively, noting that you need to satisfy the requirements of a binary sort tree
public void add(Node node) {
if (node == null) {
return;
}
//Determine the value relationship between the incoming node and the root node of the current subtree
if (node.value < this.value) {
//If the left child of the current node is null
if (this.left == null) {
this.left = node;
} else {
//Recursively add to left subtree
this.left.add(node);
}
} else {//The value of the added node is greater than that of the current node
if (this.right == null) {
this.right = node;
} else {
//Recursively add to right subtree
this.right.add(node);
}
}
//When a node is added, if: (Height of right subtree - Height of left subtree) > 1, rotate left
if (rightHeight() - leftHeight() > 1) {
//If the left subtree height of its right subtree is greater than the right subtree height of its right subtree
if (right != null && right.rightHeight() < right.leftHeight()) {
// First rotate right node (right subtree) of the current node - > right
right.rightRotate();
//Rotate left on current node
leftRotate();
} else {
//Rotate left directly
leftRotate();
}
}
if (leftHeight() - rightHeight() > 1) {
//If the right subtree of its left subtree is higher than the left subtree of its left subtree
if (left != null && left.rightHeight() > left.leftHeight()) {
//First rotate left node (left subtree) of the current node - > left
left.leftRotate();
//Rotate Right on Current Node
rightRotate();
} else {
//Rotate right directly
rightRotate();
}
return;
}
}
//Intermediate traversal
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
}
Run result:
Intermediate traversal
Node{value=6}
Node{value=7}
Node{value=8}
Node{value=9}
Node{value=10}
Node{value=11}
Before unbalanced processing~~~
Tree Height:3
Height of the left subtree:2
Height of right subtree:2
Current Root Node:Node{value=8}
Process finished with exit code 0
3. Multi-fork Tree
Basic Introduction
In a binary tree, each node has at most one data item and two child nodes. If each node is allowed to have more data items and more children, it is a multiway tree.
A multifork tree optimizes a binary tree by reorganizing nodes to reduce its height
2-3 Trees
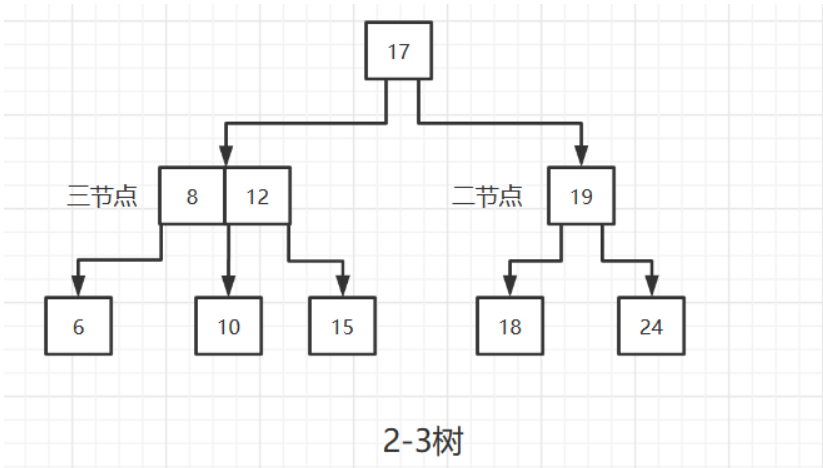
The 2-3 tree is the simplest B-tree structure with the following characteristics
- All leaf nodes of a 2-3 tree are in the same layer (as long as a B tree meets this condition)
- A node with two subnodes is called a two-node. A two-node either has no subnodes or has two subnodes
- A node with three children is called a three-node node, and the three nodes either have no children or have three children
- 2-3 trees are two-node and three-node trees (2 and 3)
2-3 tree insertion rule
- All leaf nodes of a 2-3 tree are at the same level. (A B-tree meets this criterion)
- A node with two subnodes is called a two-node. A two-node either has no subnodes or has two subnodes
- A node with three children is called a three-node node, and the three nodes either have no children or have three children
- When inserting a number to a node in accordance with the rules, the above three requirements cannot be met, it needs to be disassembled. First, it needs to be disassembled up. If the upper layer is full, it needs to be disassembled. After disassembly, it still needs to meet the above three conditions.
- The value size of a three-node subtree still follows the rules of (BST binary sort tree)
- The left subtree value is less than the parent node value
- The middle subtree value is between the values of the parent node
- The value of the right subtree is greater than that of the parent node
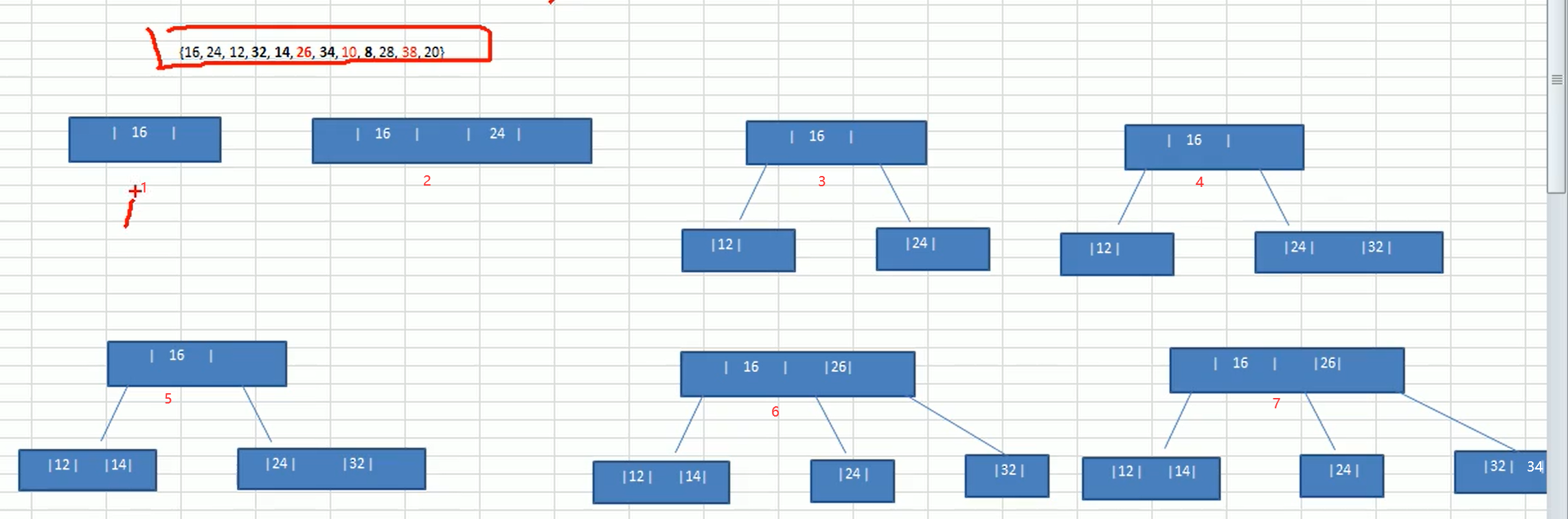
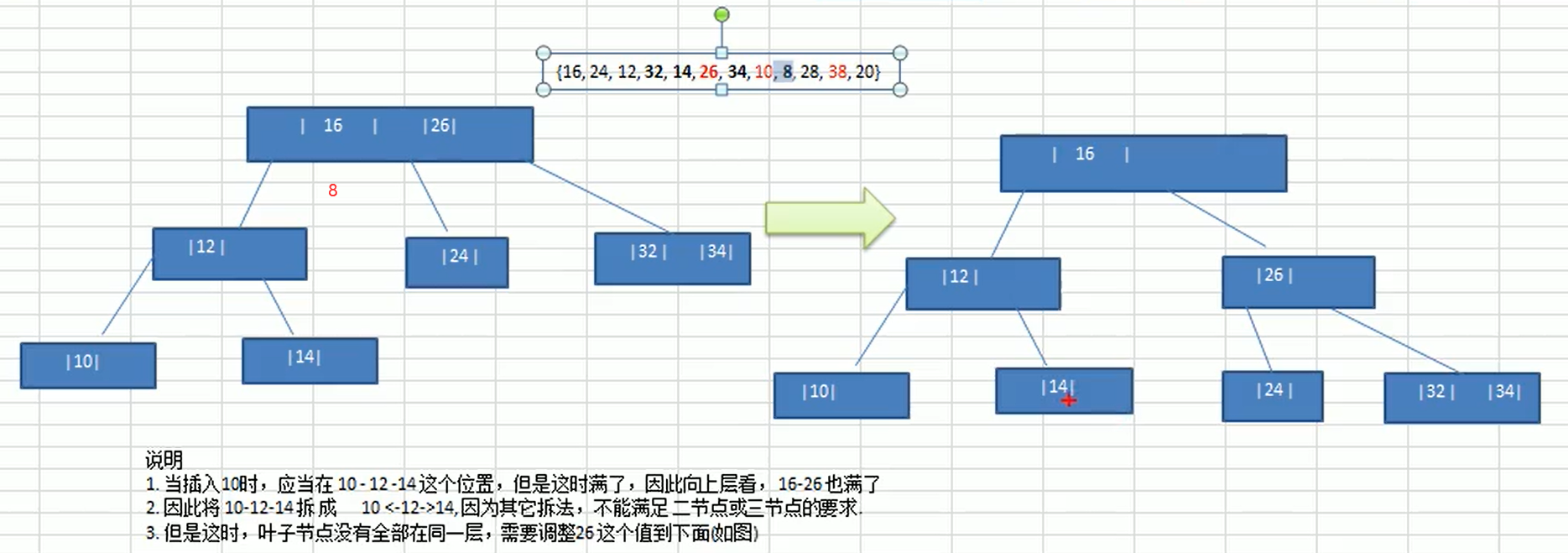
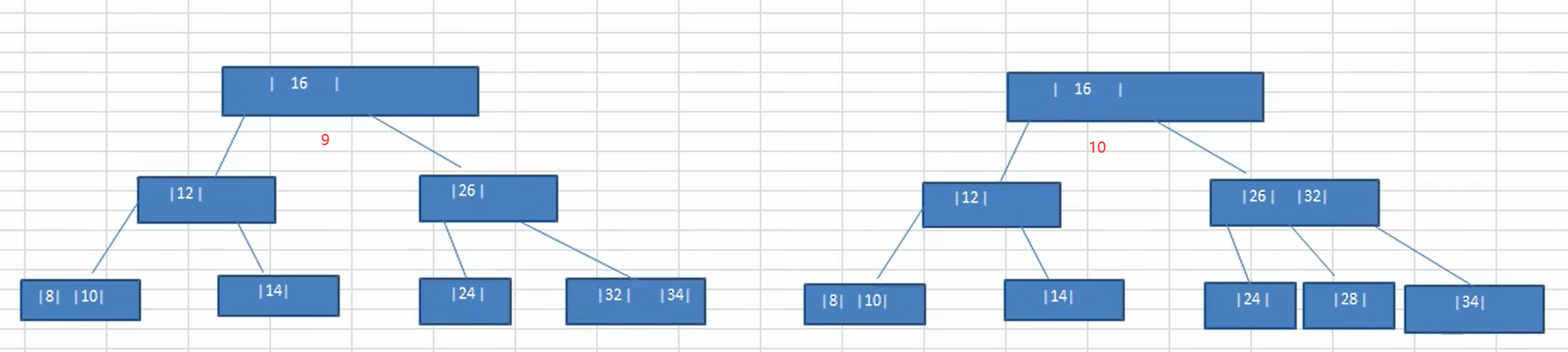
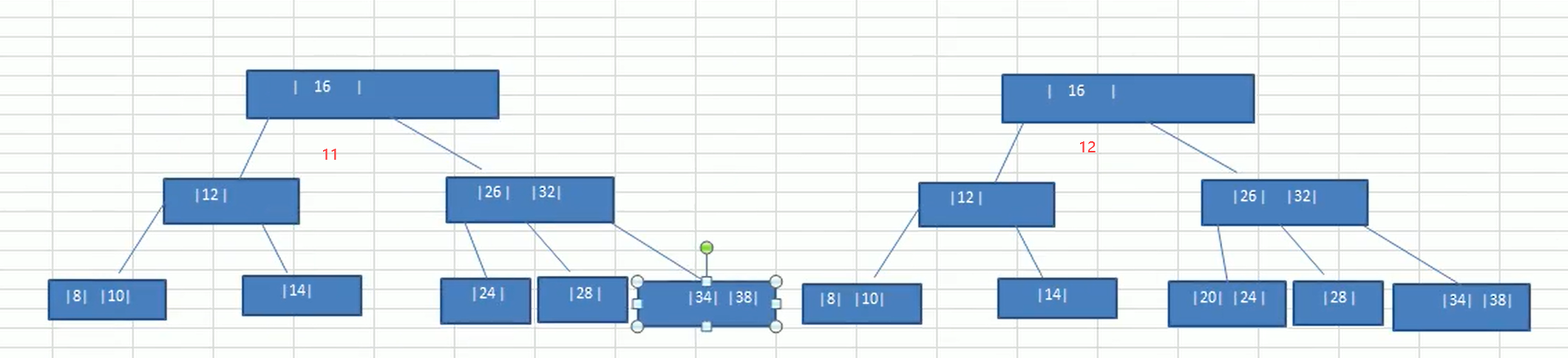
B Tree, B+and B*Tree
B-Tree
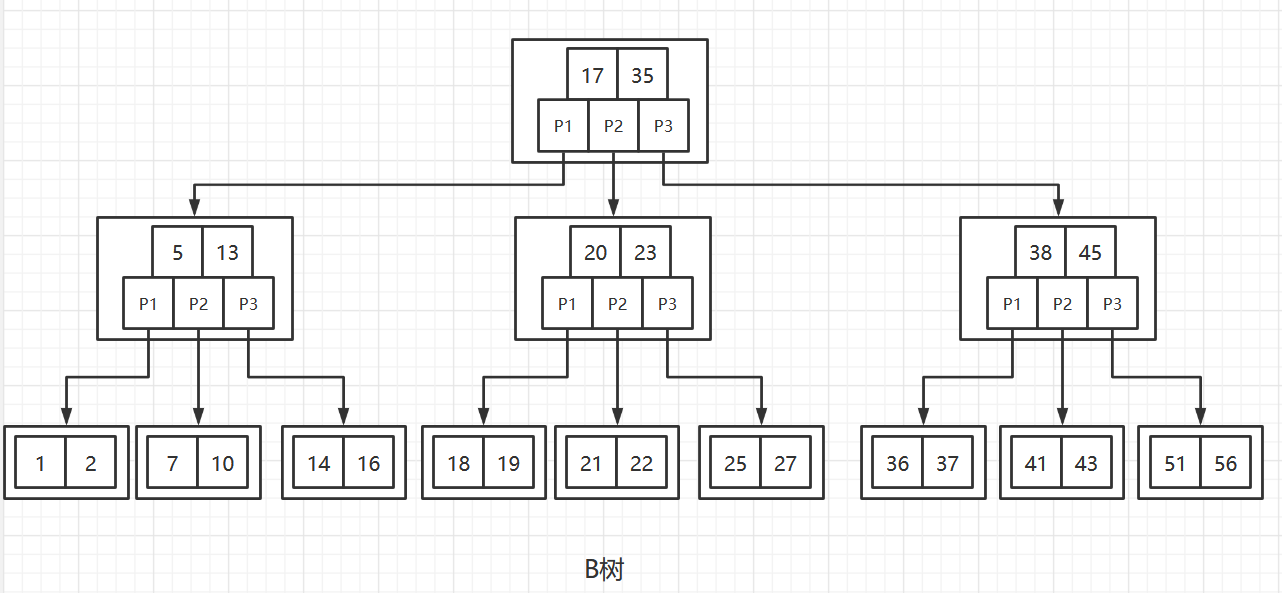
- Order of B-tree: The maximum number of children of a node. For example, the order of a 2-3 tree is 3, and the order of a 2-3-4 tree is 4
- The search of B-tree starts from the root node, and divides the sequence of keywords (ordered) within the node, and ends if hit, otherwise enters the son node within the scope of the query keyword; Repeat until the corresponding son pointer is empty or is already a leaf node
- Keyword collections are distributed throughout the tree, where both leaf and non-leaf nodes store data
- Search may end at non-leaf nodes
- Its search performance is equivalent to doing a binary search within the complete set of keywords
B+Tree
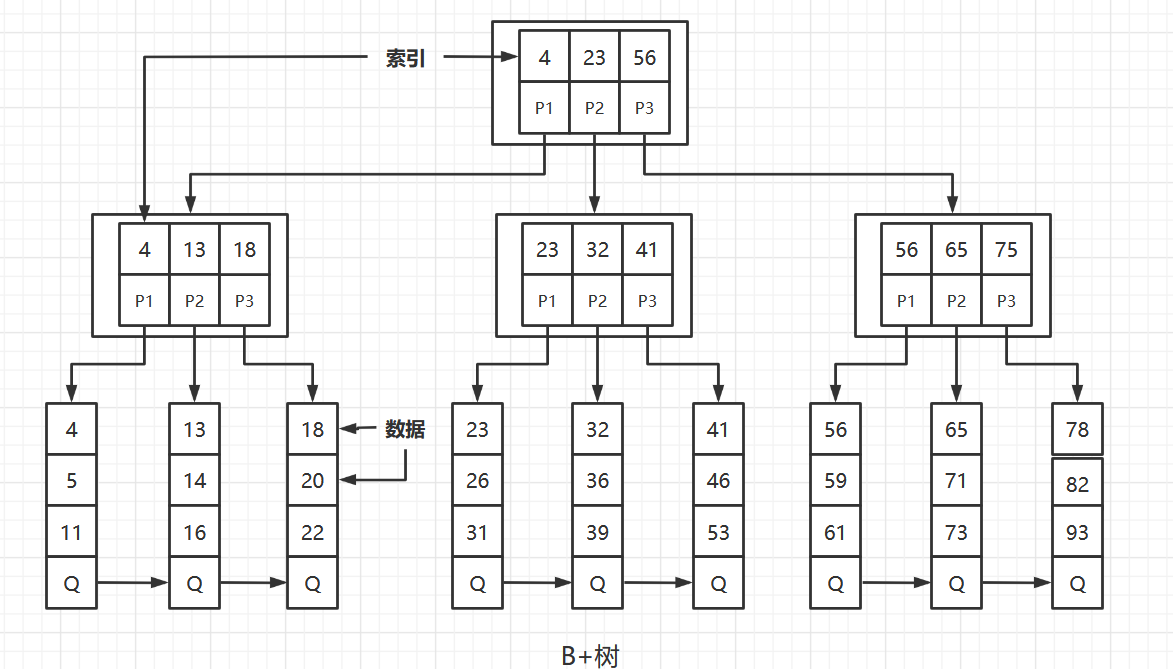
- B+Tree is a variant of B-Tree and also a multi-way search tree
- The search of B+tree is basically the same as that of B-tree, except that B+tree hits only when the leaf node is reached (B-tree can be hit at non-leaf nodes), and its performance is equivalent to doing a binary search for the entire set of keywords
- All keywords appear in the chain table of leaf nodes (that is, the data can only be in leaf nodes [also called dense index]), and the keywords (data) in the chain table are exactly ordered.
- It is not possible to hit a non-leaf node
- A non-leaf node is an index (sparse index) of a leaf node, and a leaf node is a data layer that stores (keyword) data.
- Better for file indexing systems
- B-Tree and B+Tree have their own scenarios. It cannot be said that B+Tree is better than B-Tree, and vice versa
B*Tree
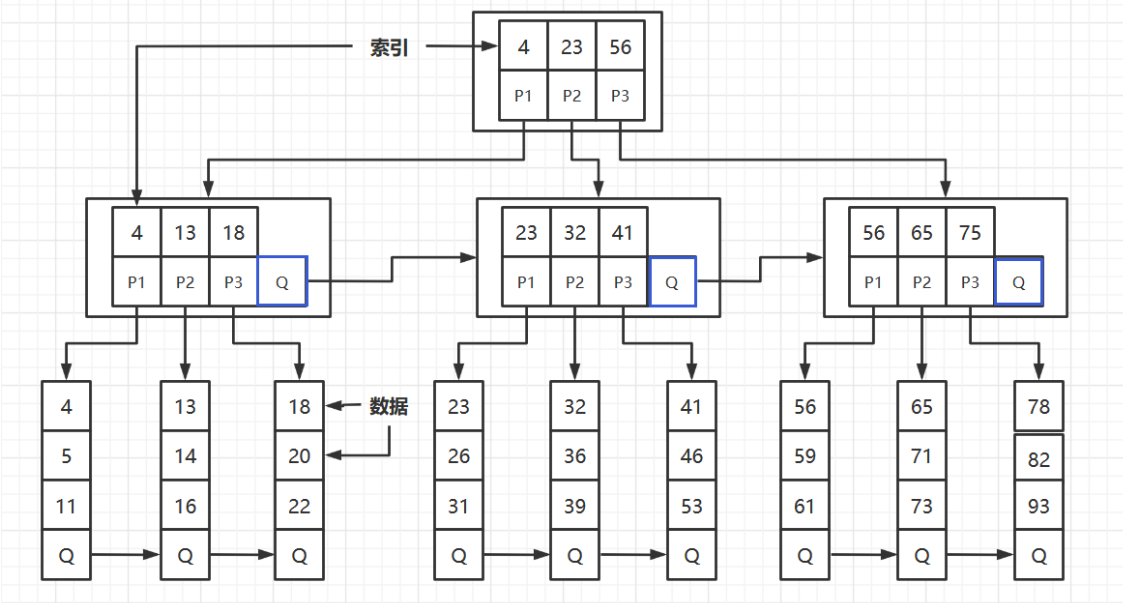
- B* Trees are variants of B+ Trees, adding pointers to brothers at non-root and non-leaf nodes of B+ Trees
- A B* tree defines at least (2/3)M of the number of non-leaf node keywords, which means that the minimum block usage is 2/3, while a B+ tree has a minimum block usage of 1/2
- From the first feature, we can see that B* trees have a lower probability of assigning new nodes and a higher space usage than B+ trees.
9. Diagram structure
1. Basic Introduction
Definition
- When we need to represent a many-to-many relationship, we need a graph
- A graph is a data structure in which nodes can have zero or more adjacent elements. The connection between two nodes is called an edge. Nodes can also be called vertices
Representation Method
adjacency matrix
- An adjacency matrix is a matrix that represents the adjacent relationship between vertices in a graph. For a graph with n vertices, row s and col s represent 1...n points.
The adjacency matrix shown above is
0 1 0 0 1 1 0 1 1 0 0 1 0 0 0 0 1 0 0 1 1 0 0 1 0
Where 0 means no connection and 1 means connected
Adjacency table
-
The adjacency matrix needs to allocate space with n edges for each vertex. In fact, many edges do not exist, which will cause a certain loss of space.
-
The implementation of adjacency tables only concerns about edges that exist, not edges that do not exist. So there's no room to waste,
An adjacency table is made up of an array + a chain table
- The index of the array represents the vertex
- The value of the element in the list represents the value of the vertex connected to that vertex
As shown in the advanced table above,
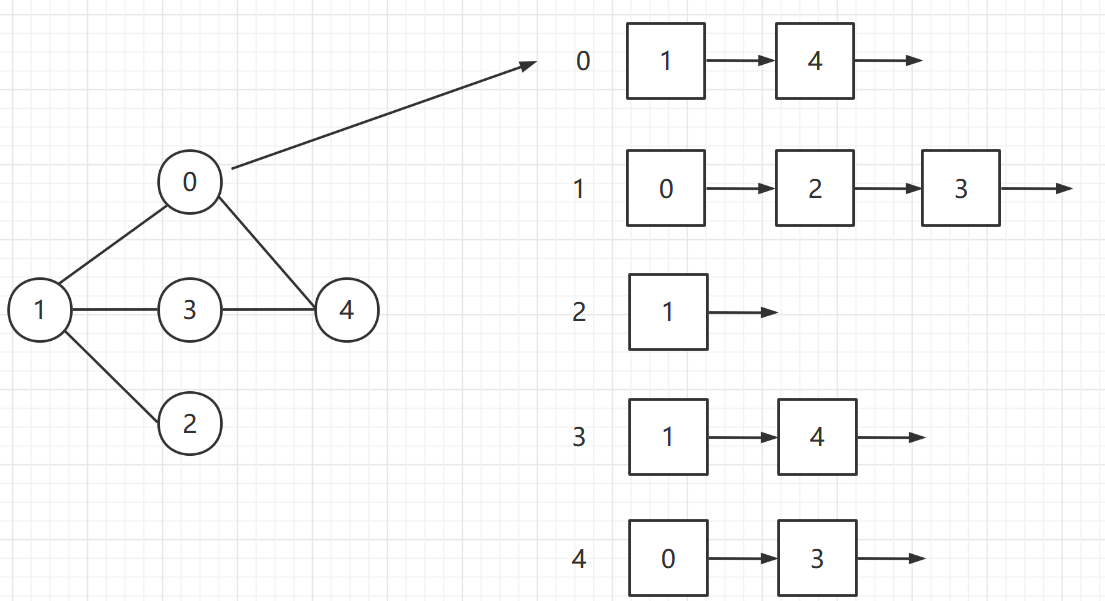
2. Creation of diagrams
Adjacency matrix creation graph
public class Graph {
private ArrayList<String> vertexList;//Store vertex set
private int[][] edges; //Neighbor Matrix Corresponding to Storage Graph
private int numOfEdges; //Represents the number of edges
public static void main(String[] args) {
//Test Diagram Create OK
int n = 5;//Number of nodes
String vertexs[] = {"A","B","C","D","E"};
//Create Graph Object
Graph graph = new Graph(n);
//Add Vertex of Loop
for (String vertex : vertexs) {
graph.insertVertex(vertex);
}
//Add Edge
graph.insertEdge(0, 1, 1);//A-B
graph.insertEdge(0, 2, 1);
graph.insertEdge(1, 2, 1);
graph.insertEdge(1, 3, 1);
graph.insertEdge(1, 4, 1);
//Show adjacency matrix
System.out.println("adjacency matrix");
graph.showGraph();
}
//constructor
public Graph(int n) {
edges = new int[n][n];
vertexList = new ArrayList<String>(n);
numOfEdges = 0;
}
//Common methods of Graphs
//Number of returned nodes
public int getNumOfVertex() {
return vertexList.size();
}
//Display the matrix corresponding to the graph
public void showGraph() {
for (int[] link : edges) {
System.out.println(Arrays.toString(link));
}
}
//Number of returned edges
public int getNumOfEdges() {
return numOfEdges;
}
//Returns data 0->"A" 1->"B" 2->"C" for node i (subscript)
public String getValueByIndex(int i) {
return vertexList.get(i);
}
//Returns the weight of v1 and v2
public int getWeight(int v1, int v2) {
return edges[v1][v2];
}
//Insert Node
public void insertVertex(String vertex) {
vertexList.add(vertex);
}
//Add Edge
/**
*
* @param v1 Indicates the subscript of a point even if the vertex "A" - "B" - >0 "B" - >1
* @param v2 Subscript corresponding to the second vertex
* @param weight Express
*/
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfEdges++;
}
}
Run result:
adjacency matrix [0, 1, 1, 0, 0] [1, 0, 1, 1, 1] [1, 1, 0, 0, 0] [0, 1, 0, 0, 0] [0, 1, 0, 0, 0] Process finished with exit code 0
3. Traversal of Graphs
The traversal of a graph is the access to a node. Depth-first traversal and breadth-first traversal of the graph
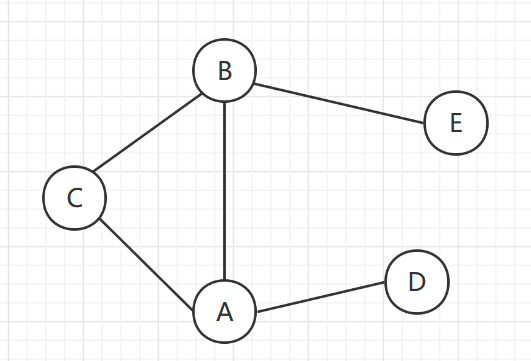
Depth first traversal (DFS)
- Depth-first traversal, starting from the initial access node, the initial access node may have multiple adjacent nodes. The strategy of depth-first traversal is to first access the first adjacent node, then use this accessed adjacent node as the initial node to access its first adjacent node. It can be understood that each time the current node is visited, the first adjacent node of the current node is visited first.
- This access strategy gives priority to mining in depth vertically rather than horizontally accessing all adjacent nodes of a node
- Depth-first search is a recursive process
thinking
- Visit the initial node v and mark the node v as visited
- Find the first adjacent node w of node v
- If w exists, continue execution 4, if w does not exist, go back to step 1, and continue from the next node of v
- If W is not accessed, do depth-first traversal recursion on w (that is, treat w as another v, then proceed to step 123)
- Find the next adjacent node of the w-adjacent node of node v and go to step 3
Implementation Code
public class Graph {
private ArrayList<String> vertexList;//Store vertex set
private int[][] edges; //Neighbor Matrix Corresponding to Storage Graph
private int numOfEdges; //Represents the number of edges
//Defined to array boolean[], records whether a node is accessed
private boolean[] isVisited;
public static void main(String[] args) {
//Test Diagram Create OK
int n = 5;//Number of nodes
String vertexs[] = {"A","B","C","D","E"};
//Create Graph Object
Graph graph = new Graph(n);
//Add Vertex of Loop
for (String vertex : vertexs) {
graph.insertVertex(vertex);
}
//Add Edge
graph.insertEdge(0, 1, 1);
graph.insertEdge(0, 2, 1);
graph.insertEdge(0, 3, 1);
graph.insertEdge(1, 2, 1);
graph.insertEdge(1, 4, 1);
//Show adjacency matrix
System.out.println("adjacency matrix");
graph.showGraph();
//dfs
System.out.println("Perform depth first traversal");
graph.dfs();
}
//constructor
public Graph(int n) {
edges = new int[n][n];
vertexList = new ArrayList<String>(n);
numOfEdges = 0;
isVisited = new boolean[5];
}
//Gets the subscript w of the first adjacent node
/**
*
* @param index
* @return Returns the corresponding subscript if it exists, otherwise returns -1
*/
public int getFirstNeighbor(int index) {
for (int j = 0; j < vertexList.size(); j++) {
if (edges[index][j] > 0) {
return j;
}
}
return -1;
}
//Get the next adjacent node based on the subscript of the previous one
public int getNextNeighbor(int v1, int v2) {
for (int j = v2 + 1; j < vertexList.size(); j++) {
if (edges[v1][j] > 0) {
return j;
}
}
return -1;
}
//Depth-first traversal algorithm
//i was 0 for the first time
public void dfs(boolean[] isVisited, int i) {
//First we access the node output
System.out.print(getValueByIndex(i) + "->");
//Set node as accessed
isVisited[i] = true;
//Find the first adjacent node of node i
int w = getFirstNeighbor(i);
while (w != -1) {//Explanations are
if (!isVisited[w]) {
dfs(isVisited, w);
}
//If the w node has already been accessed
w = getNextNeighbor(i, w);
}
}
//Overload dfs, traverse all our nodes, and DFS
public void dfs() {
//Traverse all nodes for dfs [backtracking]
for (int i = 0; i < getNumOfVertex(); i++) {
if (!isVisited[i]) {
dfs(isVisited, i);
}
}
}
//Common methods of Graphs
//Number of returned nodes
public int getNumOfVertex() {
return vertexList.size();
}
//Display the matrix corresponding to the graph
public void showGraph() {
for (int[] link : edges) {
System.out.println(Arrays.toString(link));
}
}
//Number of returned edges
public int getNumOfEdges() {
return numOfEdges;
}
//Returns data 0->"A" 1->"B" 2->"C" for node i (subscript)
public String getValueByIndex(int i) {
return vertexList.get(i);
}
//Returns the weight of v1 and v2
public int getWeight(int v1, int v2) {
return edges[v1][v2];
}
//Insert Node
public void insertVertex(String vertex) {
vertexList.add(vertex);
}
//Add Edge
/**
*
* @param v1 Indicates the subscript of a point even if the vertex "A" - "B" - >0 "B" - >1
* @param v2 Subscript corresponding to the second vertex
* @param weight Express
*/
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfEdges++;
}
}
Run result:
adjacency matrix [0, 1, 1, 1, 0] [1, 0, 1, 0, 1] [1, 1, 0, 0, 0] [1, 0, 0, 0, 0] [0, 1, 0, 0, 0] Perform depth first traversal A->B->C->E->D-> Process finished with exit code 0
Width-first Traversal (BFS)
- Similar to a hierarchical search process, breadth-first traversal requires a queue to keep the visited nodes in order to access their adjacent nodes in that order
thinking
- Access the initial node v and mark the node v as visited
- Node v Queued
- Continue execution when the queue is not empty or the algorithm ends
- Get out of the queue, get the queue head node u
- Find the first adjacent node w of node u.
- If the adjacent node w of node u does not exist, go to step 3. Otherwise, loop through the following three steps:
- If node w is not yet accessed, the node w is accessed and marked as visited
- Node w is queued
- Find the next adjacent node w of node u after the w adjacent node, and go to step 6
Implementation Code
public class Graph {
private ArrayList<String> vertexList;//Store vertex set
private int[][] edges; //Neighbor Matrix Corresponding to Storage Graph
private int numOfEdges; //Represents the number of edges
//Defined to array boolean[], records whether a node is accessed
private boolean[] isVisited;
public static void main(String[] args) {
//Test Diagram Create OK
int n = 5;//Number of nodes
String vertexs[] = {"A","B","C","D","E"};
//Create Graph Object
Graph graph = new Graph(n);
//Add Vertex of Loop
for (String vertex : vertexs) {
graph.insertVertex(vertex);
}
//Add Edge
graph.insertEdge(0, 1, 1);
graph.insertEdge(0, 2, 1);
graph.insertEdge(0, 3, 1);
graph.insertEdge(1, 2, 1);
graph.insertEdge(1, 4, 1);
//Show adjacency matrix
System.out.println("adjacency matrix");
graph.showGraph();
//dfs
//System.out.println("depth first traversal");
//graph.dfs();////A->B->C->D->E->
System.out.println();
System.out.println("Perform a breadth-first traversal");
graph.bfs();//A->B->C->D->E->
}
//constructor
public Graph(int n) {
edges = new int[n][n];
vertexList = new ArrayList<String>(n);
numOfEdges = 0;
isVisited = new boolean[5];
}
//Gets the subscript w of the first adjacent node
/**
*
* @param index
* @return Returns the corresponding subscript if it exists, otherwise returns -1
*/
public int getFirstNeighbor(int index) {
for (int j = 0; j < vertexList.size(); j++) {
if (edges[index][j] > 0) {
return j;
}
}
return -1;
}
//Get the next adjacent node based on the subscript of the previous one
public int getNextNeighbor(int v1, int v2) {
for (int j = v2 + 1; j < vertexList.size(); j++) {
if (edges[v1][j] > 0) {
return j;
}
}
return -1;
}
//Depth-first traversal algorithm
//i was 0 for the first time
public void dfs(boolean[] isVisited, int i) {
//First we access the node output
System.out.print(getValueByIndex(i) + "->");
//Set node as accessed
isVisited[i] = true;
//Find the first adjacent node of node i
int w = getFirstNeighbor(i);
while (w != -1) {//Explanations are
if (!isVisited[w]) {
dfs(isVisited, w);
}
//If the w node has already been accessed
w = getNextNeighbor(i, w);
}
}
//Overload dfs, traverse all our nodes, and DFS
public void dfs() {
//Traverse all nodes for dfs [backtracking]
for (int i = 0; i < getNumOfVertex(); i++) {
if (!isVisited[i]) {
dfs(isVisited, i);
}
}
}
//A method of breadth-first traversal of a node
private void bfs(boolean[] isVisited, int i) {
int u;//Indicates the subscript corresponding to the header node of the queue
int w;//Adjacent node w
//Queue, recording data accessed by nodes
LinkedList<Object> queue = new LinkedList<>();
//Access node, output node information
System.out.print(getValueByIndex(i) + "=>");
//Queue nodes
isVisited[i] = true;
queue.addLast(i);
while (!queue.isEmpty()) {
//Remove the header subscript of the queue
u= (Integer) queue.removeFirst();
//Gets the subscript w of the first adjacent node
w = getFirstNeighbor(u);
while (w != -1) {//find
//Have you visited
if (!isVisited[w]) {
System.out.print(getValueByIndex(w) + "=>");
//Tag has been accessed
isVisited[w] = true;
//Entry
queue.addLast(w);
}
//Use u as the precursor to find the next adjacent point behind w
w = getNextNeighbor(u, w);//Reflect our breadth preference
}
}
}
//Traverse all nodes for a breadth-first search
public void bfs() {
for (int i = 0; i < getNumOfVertex(); i++) {
if (!isVisited[i]) {
bfs(isVisited, i);
}
}
}
//Common methods of Graphs
//Number of returned nodes
public int getNumOfVertex() {
return vertexList.size();
}
//Display the matrix corresponding to the graph
public void showGraph() {
for (int[] link : edges) {
System.out.println(Arrays.toString(link));
}
}
//Number of returned edges
public int getNumOfEdges() {
return numOfEdges;
}
//Returns data 0->"A" 1->"B" 2->"C" for node i (subscript)
public String getValueByIndex(int i) {
return vertexList.get(i);
}
//Returns the weight of v1 and v2
public int getWeight(int v1, int v2) {
return edges[v1][v2];
}
//Insert Node
public void insertVertex(String vertex) {
vertexList.add(vertex);
}
//Add Edge
/**
*
* @param v1 Indicates the subscript of a point even if the vertex "A" - "B" - >0 "B" - >1
* @param v2 Subscript corresponding to the second vertex
* @param weight Express
*/
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfEdges++;
}
}
Run result:
adjacency matrix [0, 1, 1, 1, 0] [1, 0, 1, 0, 1] [1, 1, 0, 0, 0] [1, 0, 0, 0, 0] [0, 1, 0, 0, 0] Perform a breadth-first traversal A=>B=>C=>D=>E=> Process finished with exit code 0
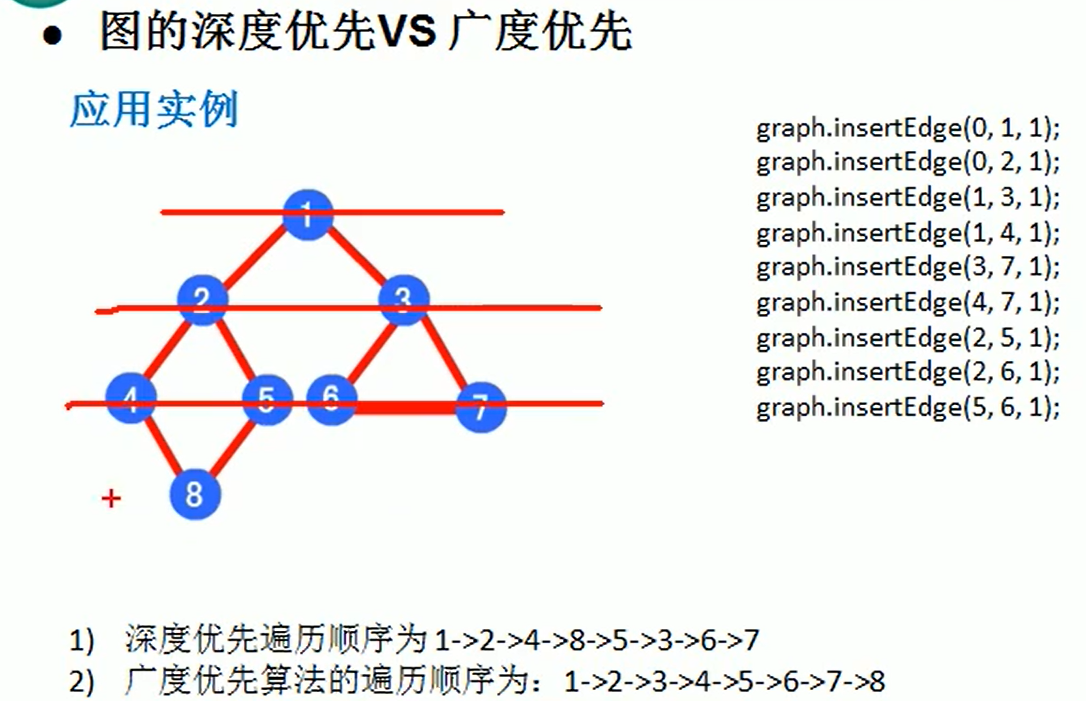
10. Algorithms
1. Binary search algorithm (non-recursive)
- Previously, we talked about the binary lookup algorithm, which uses recursion. Below, we explain the non-recursive way of the binary lookup algorithm
- The binary search algorithm is only suitable for searching from ordered columns (such as numbers and letters), sorting the columns and then searching for them
- The running time of the binary search algorithm is log2n, that is, it only needs log2n steps to find the desired target location. Assuming that the number of target 30 is found from the queue of [0,99] (100, i.e., n=100), the number of search steps is log2100, that is, it needs to find up to 7 times (26 < 100 < 2^7).
Code:
public class BinarySearchNoRecur {
public static void main(String[] args) {
//test
int[] arr = {1,3,8,10,67,100};
int index = binarySearch(arr, 100);
System.out.println("index=" +index);
}
//Non-recursive implementation of binary lookup
/**
*
* @param arr The array arr to be found is in ascending order
* @param target Number to find
* @return Returns the corresponding subscript, -1 means no found
*/
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] > target) {
right = mid - 1;//Need to look left
} else {
left = mid + 1;//Need to look right
}
}
return -1;
}
}
2. Divide and conquer algorithm
Algorithm Introduction
Divide and conquer is an important algorithm. The literal explanation is "divide and conquer", which divides a complex problem into two or more identical or similar subproblems, and then subproblems into smaller subproblems... until the final subproblem can be solved directly, the solution of the original problem is the merging of the solutions of the subproblems. This technique is the basis of many efficient algorithms, such as sorting algorithms (fast sorting, merge sorting), Fourier transforms (fast Fourier transforms)...
Basic steps
Divide and conquer has three steps in each level of recursion:
- Decomposition: Decomposition the original problem into several smaller, independent, and identical subproblems
- Solve: If the sub-problem is small and easy to solve, solve it directly, otherwise solve each sub-problem recursively
- Merge: Combine the solutions of each subproblem into the solution of the original problem
Application - Hannotta
thinking
A, B, C Towers
-
If there is only one disk, direct A->C
-
If two disks are greater than or equal, they are divided into two parts.
The bottom disk is a part, and all the disks above are a part
- Place the upper part of the disk A->B
- Lowest disk A->C
- Then put the disk B->C in B
Implementation Code
public class Hanoitower {
public static void main(String[] args) {
hanoiTower(3, 'A', 'B', 'C');
}
//The Moving Method of the Hanoi Tower
//Using a divide-and-conquer algorithm
public static void hanoiTower(int num, char a, char b, char c) {
//If there is only one disk
if (num == 1) {
System.out.println("First disc from" + a + "->" + c);
} else {
//If we have n>=2, we can always see two disks 1. The bottom disk 2. All disks above
//1. First move all the topmost disks A->B, using C
hanoiTower(num-1, a, c, b);
//2. Put the bottom disk A->C
System.out.println("No." + num + "Discs from" + a + "->" + c);
//3. Use all disks of Tower B from B->C to move to Tower A
hanoiTower(num-1, b, a, c);
}
}
}
Run result:
First disc from A->C Second disk from A->B First disc from C->B Third disc from A->C First disc from B->A Second disk from B->C First disc from A->C Process finished with exit code 0
Blog Recommendations
While brushing leetcode, I was lucky to see a blog about recursion written by a big guy, which I reloaded here.
3. Dynamic Planning
Algorithm Introduction
- The core idea of Dynamic Programming algorithm is to divide big problems into small ones and solve them so as to get the best solution step by step.
- The dynamic programming algorithm is similar to the divide and conquer algorithm in that it decomposes the problem to be solved into several subproblems, solves the subproblems first, and then derives the solution of the original problem from the solutions of these subproblems.
- Unlike the divide-and-conquer method, subproblems that are suitable for solving by dynamic programming are not always independent of each other. (that is, the solution of the next sub-stage is based on the solution of the previous sub-stage and is solved further)
- Dynamic programming can be progressively advanced by filling in tables to obtain optimal solutions
Algorithmic Application - 01 Backpack Problem
| Goods | weight | value |
|---|---|---|
| Guitar | 1 | 1500 |
| sound | 4 | 3000 |
| Computer | 3 | 2000 |
A backpack can hold up to 4kg of stuff. Seek
- Loading items maximizes the total value of the backpack and does not exceed its capacity
- Items required to be loaded cannot be duplicated (01 backpack)
Solving problems
- Backpack problem mainly refers to a given capacity of the backpack, several items with a certain value and weight, how to select items to put into the backpack to maximize the value of the items. There are 01 backpacks and full backpacks (full backpack means: every item has unlimited pieces available)
- The problem here is the 01 backpack, i.e. put at most one item per item. Infinite backpacks can be converted to 01 backpacks.
The main idea of the algorithm is to use dynamic programming to solve it. The first item to be traversed each time, depends on w[i] and v[i] to determine if it needs to be put in the backpack. That is, for a given n items, set v[i], w[i] as the value and weight of the first item, and C as the capacity of the backpack. Let the two-dimensional array v [i] [j] represent the maximum value that can be loaded into a backpack with a capacity of J in the first I items. Then we have the following results
//Indicates that the first row and the first column of the filling table are 0, mainly for convenience in representing items and capacities
(1) v[i][0]=v[0][j]=0;
// When the weight of the new item being added is larger than the current backpack capacity, use the loading strategy of the previous cell directly (the value of the item being loaded)
(2) When w[i]>j When: v[i][j]=v[i-1][j]
// When the capacity of the new item to be added is less than or equal to the capacity of the current backpack,
// Loading method:
(3) When j>=w[i]When: v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]}
v[i-1][j]: Maximum Load of Last Cell
v[i] : Indicates the value of the current commodity
w[i] : Represents the i Weight of items
v[i-1][j-w[i]] : load i-1 Goods, to remaining space j-w[i]Maximum
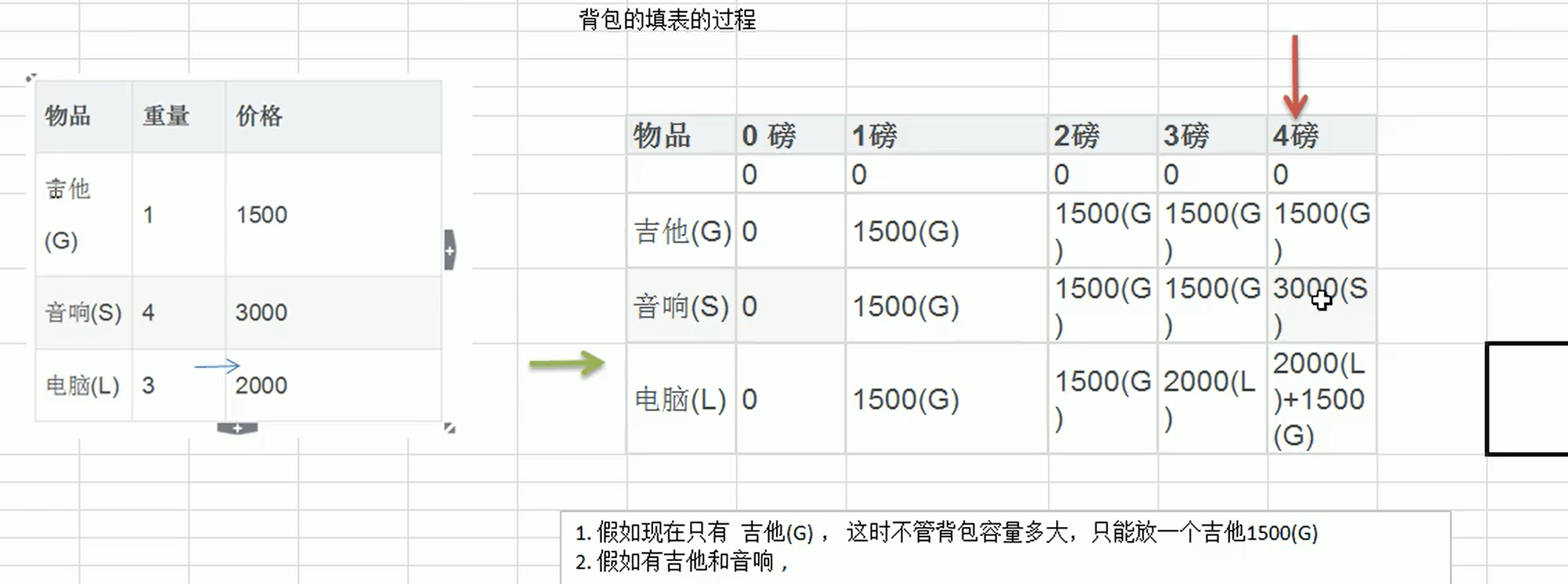
Simply put:
-
Maximum value of backpack items loaded before direct use when the loaded items have a capacity greater than the backpack
-
Compare when loading capacity is less than or equal to Backpack Capacity
- Maximum value of backpack items before loading
- After loading, the value of the item + the maximum value of the remaining capacity that can be put into the item
Select Larger
Implementation Code
public class KnapsackProblen {
public static void main(String[] args) {
int[] w = {1, 4, 3};//Weight of item
int[] val = {1500, 3000, 2000};//Value of Items
int m = 4; //Capacity of backpack
int n = val.length;//Number of items
//To record the placement of goods, define a two-dimensional array
int[][] path = new int[n+1][m+1];
//Create a two-dimensional array
//v[i][j] denotes the maximum value of a backpack with a capacity of J in the first I items
int[][] v =new int[n+1][m+1];
//Initialize the first row and column, which can be left untreated in this program because the default is 0
for (int i = 0; i < v.length; i++) {
v[i][0] = 0;//Set the first column to 0
}
for (int i = 0; i < v[0].length; i++) {
v[0][i] = 0;//Set the first line to 0
}
//Dynamic Planning Processing Based on Previous Formulas
for (int i = 1; i < v.length; i++) {//Not processing the first line i starts with 1
for (int j = 1; j<v[0].length; j++) {//Do not process the first column, j starts from 1
//formula
if (w[i-1] > j) {//Because our program I starts with 1, the w[i] in the original formula is modified to w[i-1]
v[i][j] = v[i-1][j];
} else {
//Description: Since our program i starts with 1, the formula needs to be adjusted
//v[i][j] = Math.max(v[i-1][j], val[i-1] + v[i-1][j-w[i-1]]);
//v[i][j] = Math.max(v[i-1][j], val[i-1] + v[i-1][j-w[i-1]]);
//In order to record goods stored in backpacks, we cannot use the above formula directly. We need to use if-else to represent the formula.
if (v[i-1][j] < val[i-1] + v[i-1][j-w[i-1]]) {
v[i][j] = val[i-1] + v[i-1][j-w[i-1]];
//Record current situation to path
path[i][j] = 1;
} else {
v[i][j] = v[i-1][j];
}
}
}
}
//Output once
for (int i = 0; i < v.length; i++) {
for (int j = 0; j < v[i].length; j++) {
System.out.print(v[i][j] + " ");
}
System.out.println();
}
//Export Last Placed Goods
//Maximum subscript of a two-dimensional array of storage methods, searching for storage methods from the end
int i = path.length - 1;//Maximum Subscript of Line
int j = path[0].length - 1;//Maximum Subscript of Column
while(i > 0 && j > 0) {
if(path[i][j] == 1) {
System.out.println("Will" + i + "Items in backpack");
//Backpack Remaining Capacity
j -= w[i-1];
}
i--;
}
}
}
Run result:
0 0 0 0 0 0 1500 1500 1500 1500 0 1500 1500 1500 3000 0 1500 1500 2000 3500 Put the third item in your backpack Put the first item in your backpack Process finished with exit code 0
3. KMP algorithm
KMP is a classical algorithm for resolving whether pattern strings have ever appeared in text strings and, if so, locating the earliest occurrence
Reference material: https://www.cnblogs.com/ZuoAndFutureGirl/p/9028287.html
Algorithmic Application - String Matching
Ideas and illustrations
Question: There is one string str1 = BBC ABCDAB ABCDABDE, and one substring str2=ABCDABD. Now you have to decide if str1 contains str2, if it exists, it returns to the first occurrence, if it does not, it returns -1
Algorithmic steps
- First, compare the first character of str1 with the first character of str2. That doesn't match. Keyword moves one bit backward
- Repeat the first step, or do not match, move back
- Repeat until Str1 has a character that matches the first character of Str2
- Next, compare the string to the next character of the search term, or match

- Str1 encountered a character that does not match Str2
major measure
-
At this point, the thought is to continue traversing the next character of str1, repeating step 1. (Actually, it is not wise, because BCD is already compared and there is no need to repeat the work. The basic fact is that when spaces do not match D, you actually know that the first six characters are "ABCDAB"
- The idea of the KMP algorithm is to try to take advantage of this known information, not to move the Search Location back to its already compared location, and continue to move it back, which improves efficiency
-
How can I omit the steps I just repeated? You can calculate one for str2 Partial Matching Table The generation of this table is described later
-
The partial match table for str2 is as follows
Search term A B C D A B D Partial Matching Value 0 0 0 0 1 2 0
-
-
The first six characters "ABCDAB" are matched when spaces are known to not match D. As you can see from the table, the partial match value corresponding to the last matching character B is 2, so calculate the number of digits that move backwards according to the following formula:
- Move Bit = Number of matched characters - corresponding partial match value
- Since 6 - 2 equals 4, move the search term four bits backward

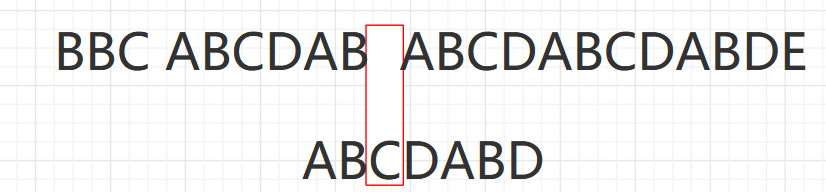
- Because the spaces do not match C, the search term continues to move backwards. At this time, the number of matched characters is 2 ("AB"), and the corresponding partial match value is 0.
So, move the number of bits = 2 - 0, and the result is 2, so move the search term back 2 bits

- Continue to move one bit back because the spaces do not match A


- Compare bit by bit until C and D do not match. So move the number of bits = 6 - 2 and continue to move the search term backwards by 4 bits
- Compare bit by bit until the last word in the search finds a perfect match, and the search is complete. If you want to continue searching (that is, find all matches), move the number of digits = 7 - 0, and move the search term backwards by 7 digits, you won't repeat it here
Partial Match Table Generation
prefixes and suffixes
- Prefix: ABCD is prefixed with [A, AB, ABC]
- Suffix: ABCD is suffixed with [BCD, CD, D]
"Partial match value" is the length of the longest common element of "prefix" and "suffix". Take "ABCDABD" for example,
- The prefix and suffix of "A" are empty sets, and the length of common elements is 0;
- "AB" is prefixed with [A], suffixed with [B], and has a common element length of 0;
- "ABC" is prefixed with [A, AB], suffixed with [BC, C], and has a common element length of 0;
- "ABCD" is prefixed with [A, AB, ABC], suffixed with [BCD, CD, D], and has a common element length of 0;
- "ABCDA" is prefixed with [A, AB, ABC, ABCD], suffixed with [BCDA, CDA, DA, A], and has a common element of "A" with a length of 1;
- "ABCDAB" is prefixed with [A, AB, ABC, ABCD, ABCDA], suffixed with [BCDAB, CDAB, DAB, AB, B], common element is "AB", length 2;
- "ABCDABD" is prefixed with [A, AB, ABC, ABCD, ABCDA, ABCDAB], suffixed with [BCDABD, CDABD, DABD, ABD, BD,D], and has a common element length of 0.
Implementation Code
public class KMPAlgorithm {
public static void main(String[] args) {
String str1 = "BBC ABCDAB ABCDABCDABDC";
String str2 = "ABCDABDC";
int[] next = kmpNext(str2);
System.out.println("Partial Matching Value next:"+ Arrays.toString(next));
int index = kmpSearch(str1, str2, next);
System.out.println("Subscript position index:"+index);
}
/**
* kmp search algorithm
* @param str1 Original string
* @param str2 Substring
* @param next A partial match table, which is a partial match table corresponding to a substring
* @return If -1 is not matched, otherwise the first matched location is returned
*/
public static int kmpSearch(String str1, String str2, int[] next) {
//ergodic
for (int i = 0, j=0; i < str1.length(); i++) {
//STR1 needs to be processed. CharAt(i)!= Str2. CharAt(j), to resize J
//Core points of kmp algorithm
while (j > 0 && str1.charAt(i) != str2.charAt(j)) {
j = next[j-1];
}
if (str1.charAt(i) == str2.charAt(j)) {
j++;
}
if (j == str2.length()) {//Eureka
return i - j + 1;
}
}
return -1;
}
//Gets a partial match value table of a string (substring)
public static int[] kmpNext(String dest) {
//Create a next array to hold partially matched values
int[] next = new int[dest.length()];
next[0] = 0;//0 if the length of the string is a partial match
for (int i = 1, j = 0; i < dest.length(); i++) {
//When dest. CharAt(i)!= Dest. CharAt(j), we need to get a new j from next[j-1]
//Until we find dest.charAt(i) == dest.charAt(j) exits when it is established
//This is the core of the kmp algorithm
while (j > 0 && dest.charAt(i) != dest.charAt(j)) {
j = next[j-1];
}
//When dest. CharAt(i) == dest. When charAt(j) is satisfied, the partial match value is + 1
if (dest.charAt(i) == dest.charAt(j)) {
j++;
}
next[i] = j;
}
return next;
}
}
Run result:
Partial Matching Value next:[0, 0, 0, 0, 1, 2, 0, 0] Subscript position index:15 Process finished with exit code 0
4. Greedy algorithm
Introduction to Algorithms
- Greedy algorithm refers to the choice of the best or the best (that is, the most favorable) choice in each step of solving a problem.
An algorithm that is expected to produce the best or best results
- The results obtained by the greedy algorithm are not necessarily optimal (sometimes optimal), but are results of relatively similar (near) optimal solutions.
Algorithmic Application - Set Coverage
Suppose that there are radio stations that need to be paid below, as well as the areas covered by the station signals. How to select the fewest stations so that all regions can receive signals
| radio station | Number of coverage areas | Coverage Area |
|---|---|---|
| K1 | 0 | Beijing, Shanghai, Tianjin |
| K2 | 0 | Guangzhou, Beijing, Shenzhen |
| K3 | 0 | Chengdu, Shanghai, Hangzhou |
| K4 | 0 | Tianjin, Shanghai |
| K5 | 0 | Dalian, Hangzhou |
Ideas and illustrations
thinking
- Traverse through all the radio stations and find one that covers the most uncovered areas (this station may contain some covered areas, but it doesn't matter)
- Add this station to a collection (such as ArrayList) and find ways to remove the area it covers from the next comparison.
- Repeat step 1 until all areas are covered
graphic

-
Traversing through the coverage area of the radio station, we found that K1 covers the most areas, and removed the area covered by K1 from the regional collection. Then put K1 in the radio collection and update the number of coverage areas
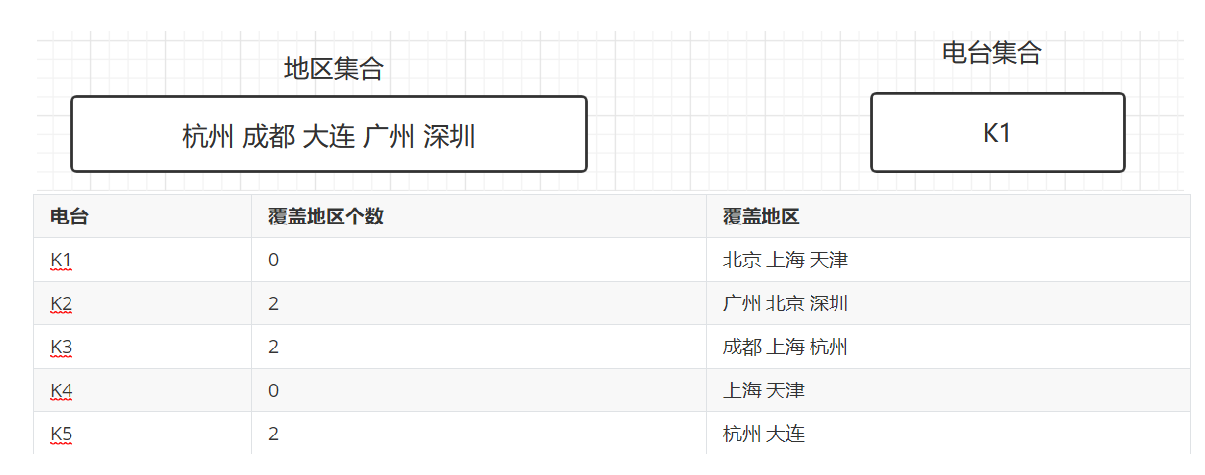
-
Traversing, it is found that K2 covers the most areas, and the areas covered by K2 are removed from the regional collection. Then put K2 in the radio collection and update the number of coverage areas
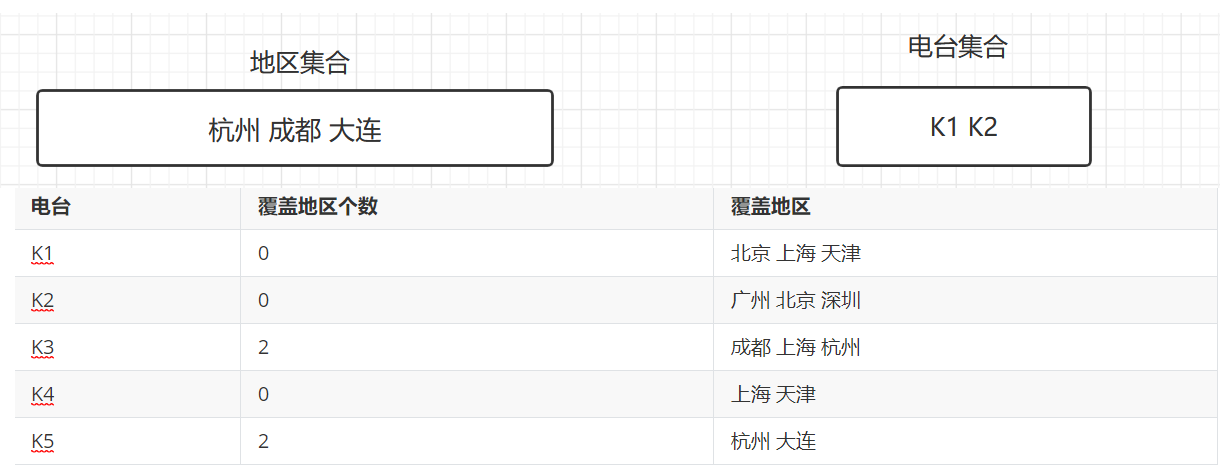
-
Traversing, it is found that K3 covers the most areas, and the areas covered by K3 are removed from the regional collection. Then put K3 in the radio collection and update the number of coverage areas
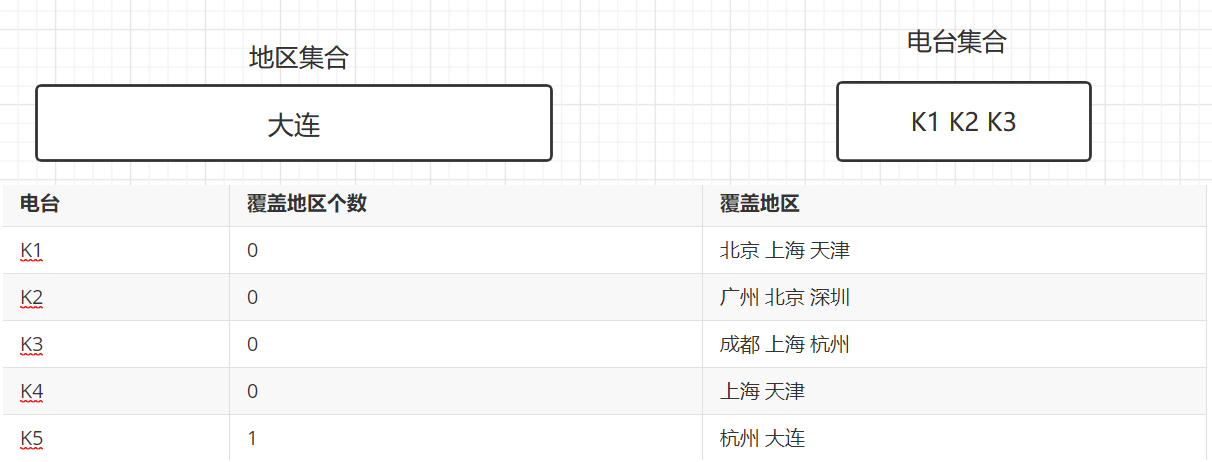
- Traversing, it is found that K5 covers the most areas, and the areas covered by K5 are removed from the regional collection. Then put K5 in the radio collection and update the number of coverage areas. All areas are covered and the algorithm ends

5. Prim algorithm
Algorithm Introduction
The Prim algorithm finds the smallest spanning tree, that is, in a graph containing n vertices, a connected subgraph with only (n-1) edges containing all n vertices, also known as the minimal connected subgraph
minimum spanning tree
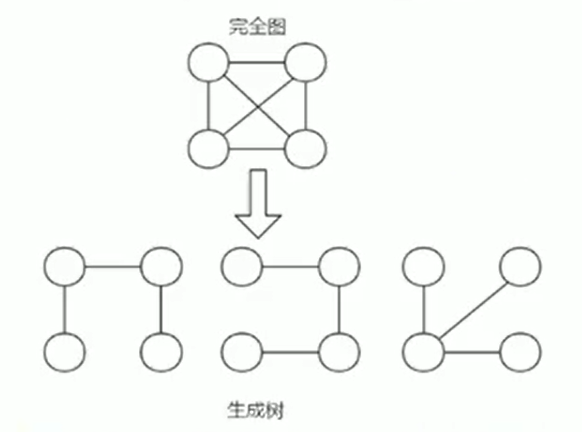
- Given a weighted undirected connected graph, the sum of the weights on all edges of the tree is minimized, which is called the minimum spanning tree.
- N vertices, there must be N-1 edges
- Contains all vertices
- N-1 edges in the graph
- The main algorithms for finding the minimum spanning tree are the Prim algorithm and the Kruskal algorithm
Application Scenarios
-
Shengli Township has seven villages (A,B,C,D,E,F,G), and now needs to build roads to connect them
-
Distance between villages is represented by a side line (weight), e.g. A-B distance of 5 kilometers
-
Question: How to build roads so that all villages can be connected and the total mileage of road construction is the shortest?
Idea: Connect 10 edges, but the total mileage is not the minimum
The right idea is to choose as few routes as possible, with each route being the smallest and the total mileage being the least
Graphical analysis:
-
from