1. Single valued binary tree
– oj link

Solution:
1. Judge whether the value of the left child of the root is the same as the root node.
2. Judge whether the value of the right child of the root is the same as the root node.
3. Judge whether the binary tree with the left child of the root as the root is a single valued binary tree.
4. Judge whether the binary tree with the right child of the root as the root is a single valued binary tree. If the above conditions are met, it is a single valued binary tree.
Note: an empty tree is also a single valued binary tree.
code:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isUnivalTree(TreeNode* root) {
if(root==NULL)//The root is empty and is a single valued binary tree
return true;
if(root->left&&root->left->val!=root->val)//The left child exists, but the value of the left child is not equal to the value of the root
return false;
if(root->right&&root->right->val!=root->val)//The right child exists, but the value of the right child is not equal to the value of the root
return false;
return isUnivalTree(root->left)&&isUnivalTree(root->right);//The left subtree is a single valued binary tree and the right subtree is a single valued binary tree (recursive)
}
};
2. Check whether the two trees are the same
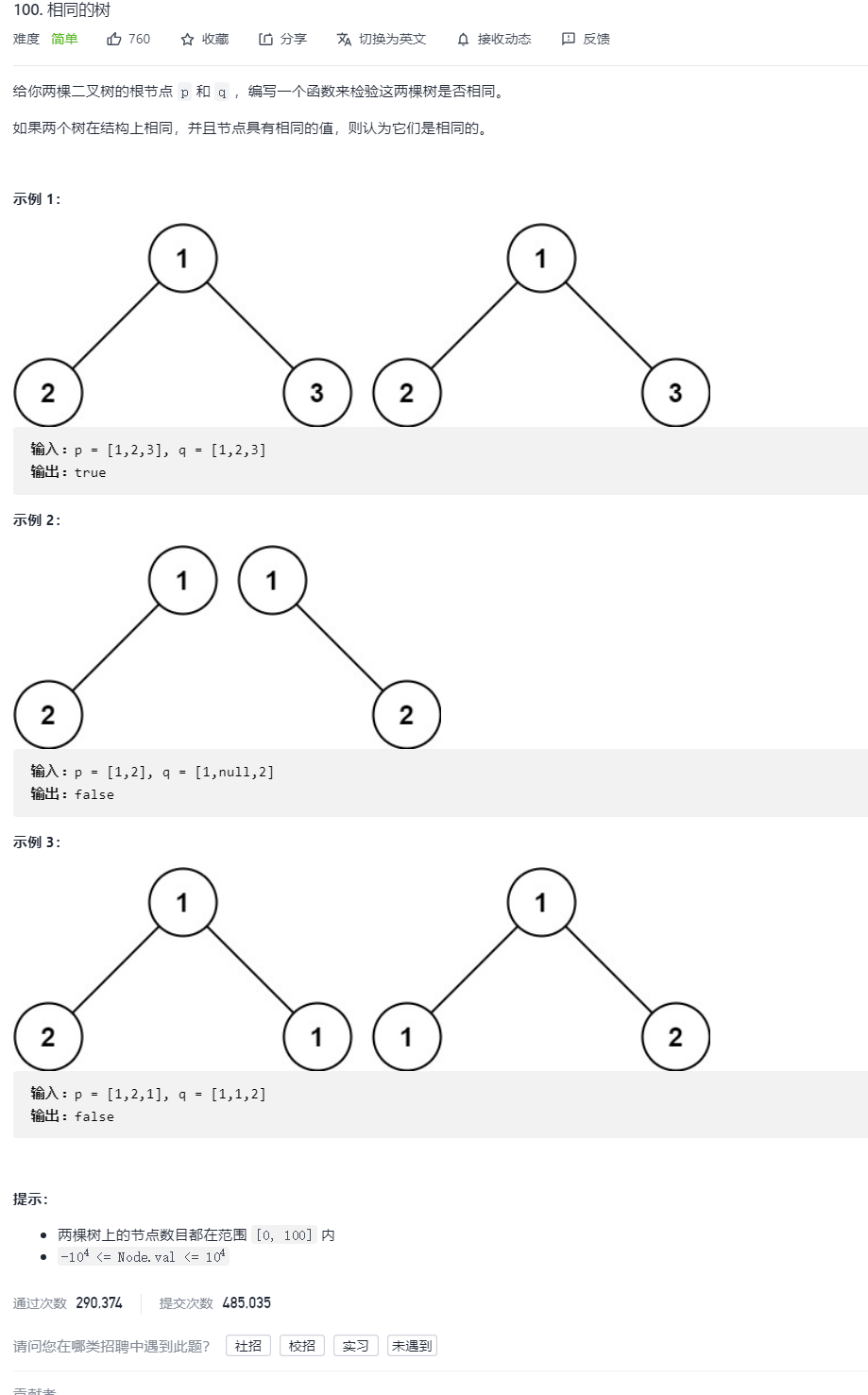
Solution:
To judge whether the two binary trees are the same, you can also decompose them into sub problems:
1. Compare whether the roots of two trees are the same.
2. Compare whether the two left subtrees are the same.
3. Compare whether the two right subtrees are the same.
code:
//Judge whether two binary trees are the same
bool isSameTree(BTNode* p, BTNode* q)
{
if (p == NULL&&q == NULL)//If both trees are empty, they are the same
return true;
if (p == NULL || q == NULL)//If only one of the two trees is empty, it is different
return false;
if (p->data != q->data)//If the values of two tree roots are different, they are different
return false;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);//If the left subtree and the right subtree of two trees are the same, the two trees are the same
}
3. Symmetric binary tree
– oj link
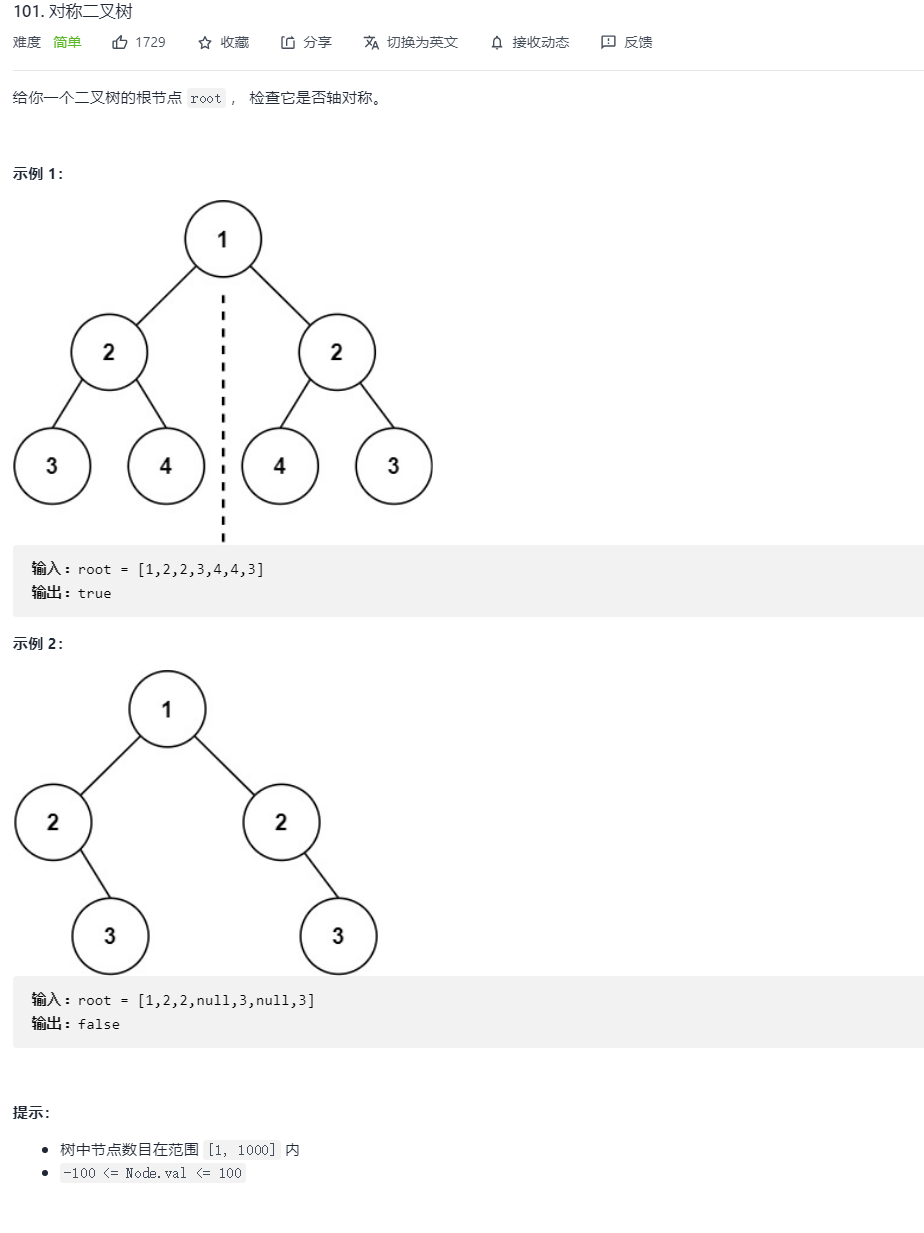
Solution:
To judge whether a binary tree is symmetric, judge whether the left and right subtrees of its root node are mirror symmetric. If it is found that the values of two nodes with mirror symmetry are different during traversal, there is no need to continue traversal.
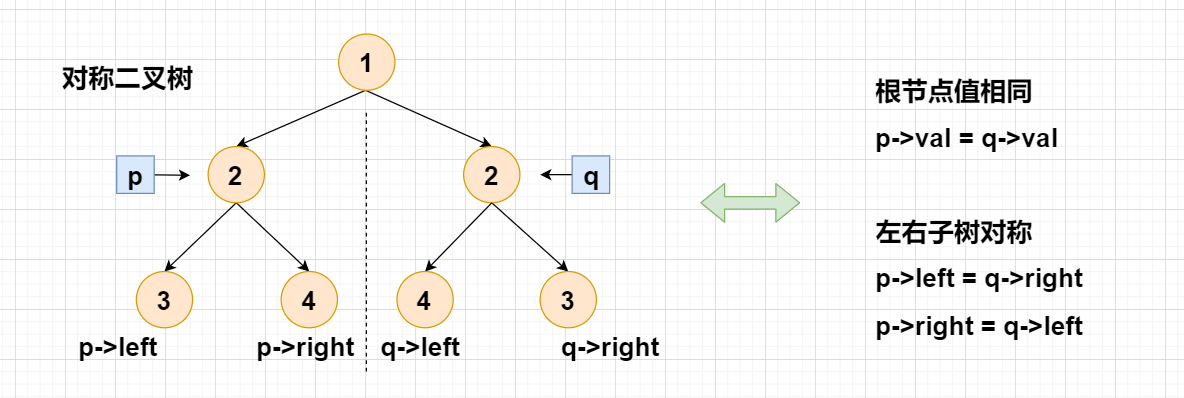
code:
//Judge whether the mirror positions are equal
bool travel(BTNode* root1, BTNode* root2)
{
if (root1 == NULL&&root2 == NULL)//The red and blue tracks traverse to NULL at the same time, and the function returns
return true;
if (root1 == NULL || root2== NULL)//In the red and blue pointers, one is NULL and the other is not NULL, that is, the images are not equal
return false;
if (root1->val!= root2->val)//The red and blue pointers point to different node values, that is, the images are not equal
return false;
//Subproblem: left subtree traversal order: first left then right, right subtree traversal order: first right then left. If both traversals are successful, it is a symmetric binary tree
return travel(root1->left, root2->right) && travel(root1->right, root2->left);
}
//Symmetric binary tree
bool isSymmetric(BTNode* root)
{
if (root == NULL)//An empty tree is a symmetric binary tree
return true;
return travel(root->left, root->right);//Judge whether the mirror positions are equal
}
4. A subtree of another tree
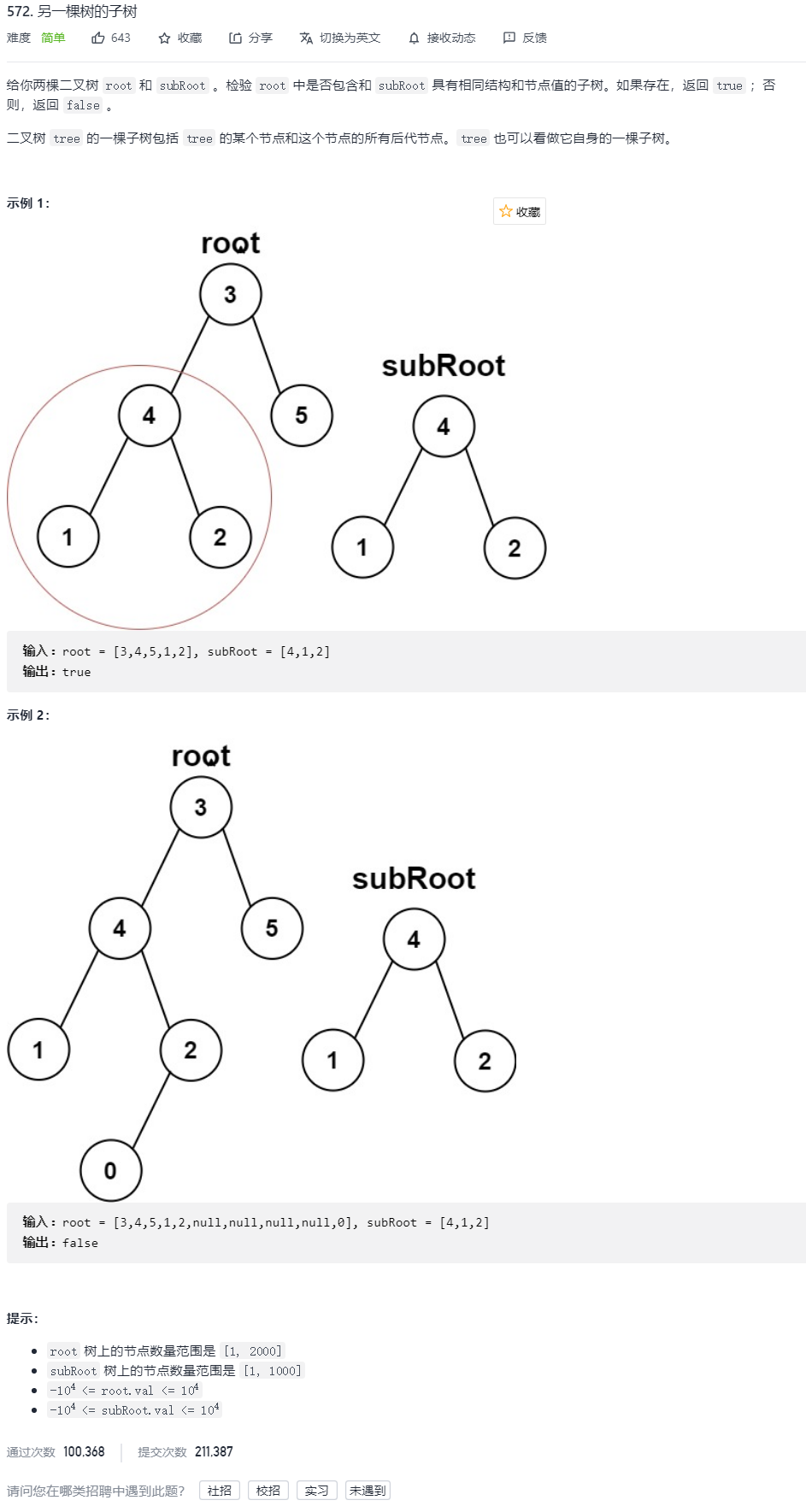
Solution:
Idea:
If a tree is a subtree of another tree, either the two trees are equal, or the tree is a subtree of the left tree or the right tree of the tree.
Implemented with two layers of recursion:
The isSameTree function is used to recursively check whether the corresponding nodes of the tree to be judged are the same (that is, judge the same binary tree);
The isSubtree function is used to determine whether the subRoot is a subtree of root;
code:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
//Check whether the two trees are the same
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if(p==NULL&&q==NULL)
return true;
if(p==NULL||q==NULL)
return false;
if(p->val!=q->val)
return false;
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
//Determine whether the subRoot is a subtree of root
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
if(root==NULL)//Empty tree, which cannot be the same as subRoot (subRoot is not empty)
return false;
if(isSameTree(root,subRoot))//Take root and subRoot as the roots and start to compare whether the two trees are the same
return true;
//Judge whether one of the left and right children of root is the same as subRoot
return isSubtree(root->left,subRoot)||
isSubtree(root->right,subRoot);
}
5. Construction and traversal of binary tree
– oj link
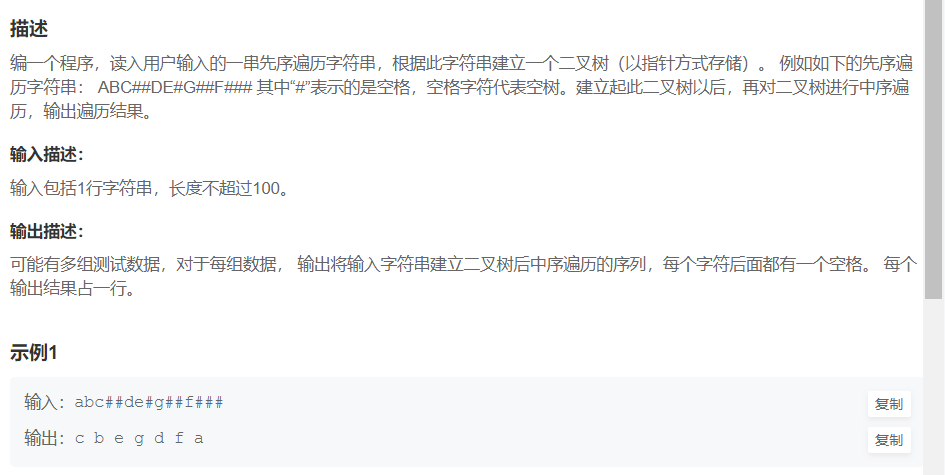
Solution:
According to the string obtained by previous traversal, we can easily draw its corresponding binary tree:
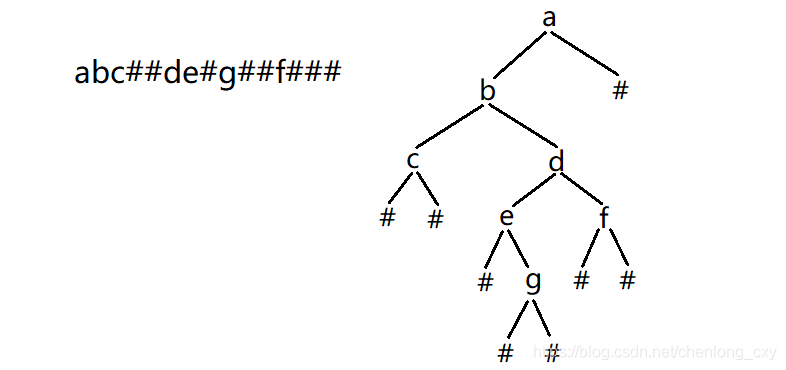
We can read characters from the string in turn:
1. If the character is not #, we first construct the node of the value, and then recursively construct its left subtree and right subtree.
2. If the character is #, it means that no more nodes can be built under this position. Just return.
After building the tree, use the middle order traversal to print the data of the binary tree.
#include <stdio.h>
#include <stdlib.h>
typedef struct TreeNode
{
struct TreeNode* left;
struct TreeNode* right;
char data;
}TreeNode;
//Create tree
TreeNode* CreateTree(char* str, int* pi)
{
if(str[*pi] == '#')//
{
(*pi)++;
return NULL;
}
//Not NULL, build node
TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
root->data = str[*pi];
(*pi)++;
//Recursive construction of left subtree
root->left = CreateTree(str, pi);
//Recursive construction of right subtree
root->right = CreateTree(str, pi);
return root;
}
//Middle order traversal
void Inorder(TreeNode* root)
{
if(root == NULL)
return;
Inorder(root->left);
printf("%c ", root->data);
Inorder(root->right);
}
int main()
{
char str[100];
scanf("%s", str);
int i = 0;
TreeNode* root = CreateTree(str, &i);
Inorder(root);
return 0;
}
6. Preorder traversal of binary tree
– oj link
Solution:
Preorder Traversal (also known as Preorder Traversal) - the operation of accessing the root node occurs before traversing its left and right subtrees
Idea:
1. Firstly, the number of nodes in the binary tree is calculated to determine the size of the dynamically opened array.
2. Traverse the binary tree and store the traversal results in the array.
3. Returns an array.
code:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int TreeSize(struct TreeNode* root)//Find the number of nodes of the tree
{
if(root==NULL)
return 0;
return TreeSize(root->left)+TreeSize(root->right)+1;
}
void _preorderTraversal(struct TreeNode* root,int *arr,int *pi)//Put the values of nodes in the tree into an array
{
if(root==NULL)
{
return;
}
//Preorder traversal
arr[(*pi)++]=root->val;//First put the value of the root node into the array
_preorderTraversal(root->left,arr,pi);//Then put the values of the nodes in the left subtree into the array
_preorderTraversal(root->right,arr,pi);//Finally, put the values of the nodes in the right subtree into the array
}
int* preorderTraversal(struct TreeNode* root,int *returnSize)
{
*returnSize=TreeSize(root);
int *arr=malloc(sizeof(int)* *returnSize);
int i=0;
_preorderTraversal(root,arr,&i);
return arr;
}
The principle of middle order and post order traversal is similar, but there is a difference in the recursive order
7. Middle order traversal of binary tree
– oj link
code:
//Find the number of nodes of the tree
int TreeSize(struct TreeNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//Put the values of nodes in the tree into an array
void inorder(struct TreeNode* root, int* arr, int* pi)
{
//Middle order traversal
if (root == NULL)//If the root node is empty, return directly
return;
inorder(root->left, arr, pi);//First, put the values of nodes in the left subtree into the array
arr[(*pi)++] = root->val;//Then put the value of the root node into the array
inorder(root->right, arr, pi);//Finally, put the values of the nodes in the right subtree into the array
}
int* inorderTraversal(struct TreeNode* root, int* returnSize)
{
*returnSize = TreeSize(root);//The number of values is equal to the number of nodes
int* arr = (int*)malloc(sizeof(int)*(*returnSize));
int i = 0;
inorder(root, arr, &i);//Put the values of nodes in the tree into an array
return arr;
}
8. Post order traversal of binary tree
– oj link
 code:
code:
int TreeSize(struct TreeNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//Put the values of nodes in the tree into an array
void postorder(struct TreeNode* root, int* arr, int* pi)
{
//Postorder traversal
if (root == NULL)//If the root node is empty, return directly
return;
postorder(root->left, arr, pi);//First, put the values of nodes in the left subtree into the array
postorder(root->right, arr, pi);//Put the value of the last node in the array subtree
arr[(*pi)++] = root->val;//Then put the value of the root node into the array
}
int* postorderTraversal(struct TreeNode* root, int* returnSize){
*returnSize = TreeSize(root);//The number of values is equal to the number of nodes
int* arr = (int*)malloc(sizeof(int)*(*returnSize));
int i = 0;
postorder(root, arr, &i);//Put the values of nodes in the tree into an array
return arr;
}