Algorithm divide and conquer

1 algorithm idea

A problem with scale n is divided into k smaller subproblems, which are independent and the same as the original problem. Then these subproblems are solved recursively, and the solutions of the subproblems are combined to obtain the solution of the original problem.

2 examples

2.1 binary search

Binary search is a typical example of using divide and conquer.
Given the sorted set of n elements a[0:n-1], find a specific element x. The dichotomy divides n elements into two parts with roughly the same number, and compares a[n/2] with x.
If \ (x < a [n / 2] \), search in a[0:n/2];
If \ (x=a[n/2] \), find X;
If \ (x > a [n / 2] \), search in a[n/2:n-1]. Specific algorithm examples are as follows.

template<typename T>
int BinarySearch(T a[], int lo, int hi){
    //Find the position of x in the collection, otherwise - 1 is returned
    while(lo <= hi){
        int mid = lo + (hi - lo)/2;
        if(x == a[mid])   return mid;
        else if(x < a[mid])     hi = mid - 1;
        else lo = mid + 1;
    }
    return -1;
}

2.2 large integer multiplication

Let X and Y be n-bit binary integers and calculate their product XY. If the method of bit-by-bit multiplication is used, the complexity of \ (O(n^2) \) is required. If divide and conquer is used, large integers can be calculated more efficiently.

Divide X and Y into two segments respectively, and the length of each segment is n / 2 (the high and low positions of X are recorded as A and B, and the high and low positions of Y are recorded as C and D). Thus, it can be calculated that

\(X=A*2^{\frac{n}{2}}+B,\)

\(Y=C*2^{\frac{n}{2}}+D，\)

\(XY=(AC*2^{\frac{n}{2}}+(AD+BC)*2^{\frac{n}{2}}+BD)\).
However, if XY is calculated in this way, such as 4 times of n/2 multiplication, 3 times of addition not exceeding 2n bits, and two shifts, it is not more effective than direct calculation. Therefore, we optimize the calculation by decomposing AD+BC,

In this way, only three multiplications are required, and the complexity can be reduced to \ (O(n^{log3}) \).

typedef long long ll;
ll multipy(ll x, ll y, int num)
{
    int s = (x > 0) && (y > 0) ? 1 : -1;
    x = (x > 0) ? x : -x;
    y = (y > 0) ? y : -y;
    if (num == 0)	//Recursive exit
        return 0;
    else if (num == 1)	//Single digit direct multiplication
        return s * x * y;
    else
    {
        ll A = x / (int)pow(10, (int)(num / 2));	//Gets the high order of X
        ll B = x % (int)pow(10, (int)(num / 2));	//Get the low order of X
        ll C = y / (int)pow(10, (int)(num / 2));	//Gets the high order of Y
        ll D = y % (int)pow(10, (int)(num / 2));	//Get the low order of Y

        ll AC = multipy(A, C, (int)(num / 2));		//Recursive calculation AC
        ll BD = multipy(B, D, (int)(num / 2));		//Recursive calculation BD
        ll ABDC = multipy(A - B, D - C, (int)(num / 2)) + AC + BD;	//Recursive computation (A-B)(D-C)
        return s * (ll)(AC * (int)pow(10, (int)(num / 2) + (int)(num / 2)) + ABDC * (int)pow(10, (int)(num / 2)) + BD);
    }
}

2.3 quick sort

Quick sort is also a sort method based on divide and conquer.

For a given array a[p:r], sort as follows.

1. Find the separation point and divide the array a[p:r] into three segments. Any element is smaller than the separation point, and any element is larger than the separation point.
2. Recursive quick sort of subarray
3. Merge array

The running time of quick sort is related to whether the partition is symmetrical.
In the worst case, the number of two areas divided each time contains n-1 elements and 1 element respectively. At this time, the time complexity of Partition is \ (O(n) \). If this is the case for each division, the complexity of quick sorting will reach \ (O(n^2) \).
In the best case, the benchmark for each partition is exactly the median, and the size of the two regions for each partition is n/2. At this time, the complexity of quick sorting will be reduced to \ (O(nlogn) \).
It is proved that in the average case, the time complexity of quick sorting is also \ (O(nlogn) \).

template <typename T>
int Partition(T a[], int lo, int hi)
{
    int i = lo, j = hi + 1;
    T temp = a[lo];
    while (true)
    {
        while (a[++i] < temp)	//Place less than the separation point on the left segment
            ;
        while (a[--j] > temp)	//Place greater than the separation point on the left segment
            ;
        if (i >= j)
            break;
        swap(a[i], a[j]);
    }
    swap(a[lo], a[j]);
    return j;
}

template <typename T>
void QuickSort(T a[], int lo, int hi)
{
    if (lo < hi)
    {
        int j = Partition(a, lo, hi);	//Find separation point
        QuickSort(a, lo, j - 1);	//Sort the left segment
        QuickSort(a, j + 1, hi);	//Sort the right segment
    }
}

2.4 closest point pair problem

Given n points on the plane, find a pair of points so that the distance of the point pair is the smallest among all the point pairs composed of n points.

The most intuitive solution is to compare each point with other n-1 points to find the minimum distance. The complexity is \ (O(n^2) \).

If we adopt the divide and conquer method, we can reduce the complexity to \ (O(nlogn) \).

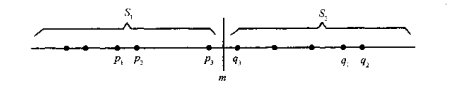
In the one-dimensional case, we divide the set s into S1 and S2 by m points.
Thus, all points P in S1 and Q in S2 have p < Q. Recursively find the nearest point pair on S1 and S2 and set d=min(|p1-p2|,|q1-q2|). Then the nearest point pair in S is either (p1,p2), (q1,q2) or (p3,q3). If the nearest point pair of S is (p3,q3), the distance between p3 and q3 and m does not exceed d, and there is only one point in each interval (m-d,d] and (d,m+d]. In this way, the merging can be completed in linear time.

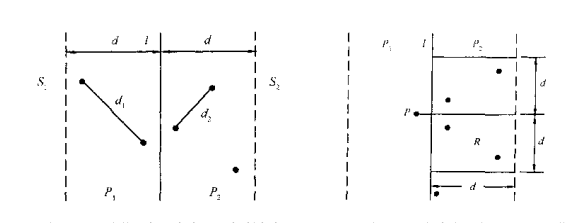
In the two-dimensional case, as can be seen from the above figure, the band with a width of 2d may have at most n points, and the merging time is \ (n^2 \) in the worst case. However, the points in P1 and P2 have the following sparse properties. For any point in P1, the points in P2 must fall in a rectangle of \ (d*2d \), and only six points need to be checked at most.

struct Point{
    double x,y;
}point[N];

int n;
int temp[N];

double Cpair(int left, int right){
    double d = 1e20;
    //Recursive exit
    if(left==right) return d;
    if(left+1 == right) return dis(left,right);
    int mid = left + (right-left)/2;
    double d1 = Cpair(left,mid);	//Recursively find the shortest distance to the left
    double d2 = Cpair(mid+1,right);	//Recursively find the shortest distance to the right
    d = min(d1,d2);
    int i,j,k=0;
    //Find the set of points within d from the center line
    for(i = left; i <= right; ++i){
        if(fabs(point[mid].x-point[y].x)<=d)
            temp[k++] = i;
    }
    sort(temp,temp+k);
    //Linear scan
    for(i = 0; i < k; i++){
        for(j = i + 1; j <k&&point[temp[i]].y-point[temp[i]].y<d;j++){
            double d3 = dis(temp[i],temp[j]);
            if(d>d3)
                d=d3;
        }
    }
    return d;
}