At this time, there are only two elements in the array, so we only need to constantly compare the sizes of child elements in the two elements to obtain a complete ordered array, as shown in the following figure:

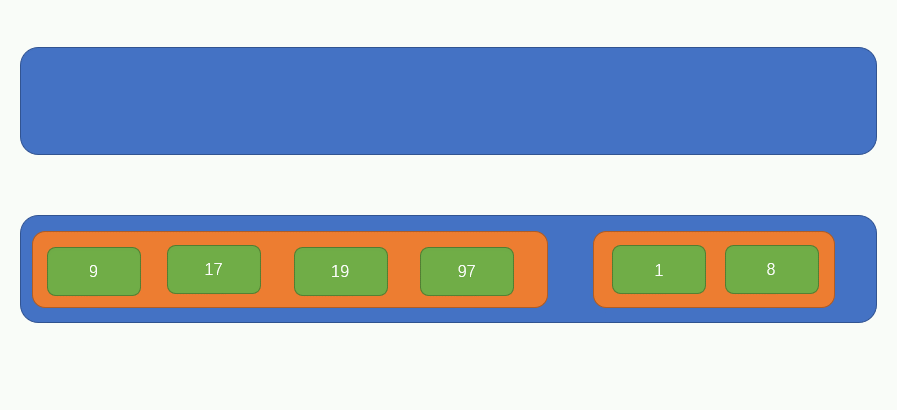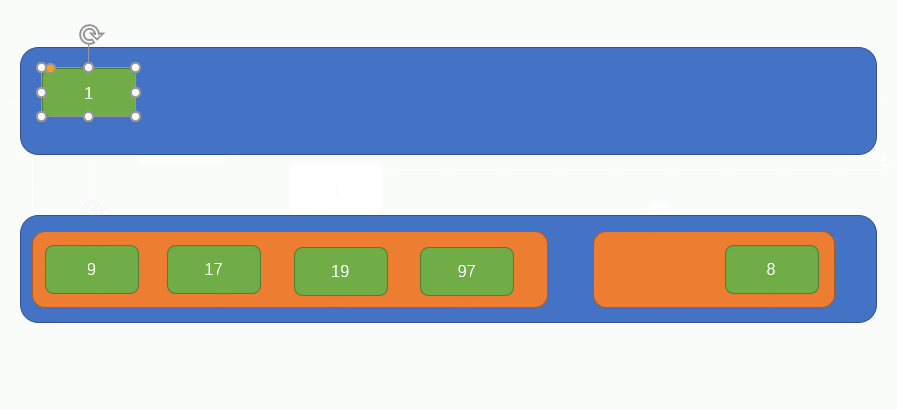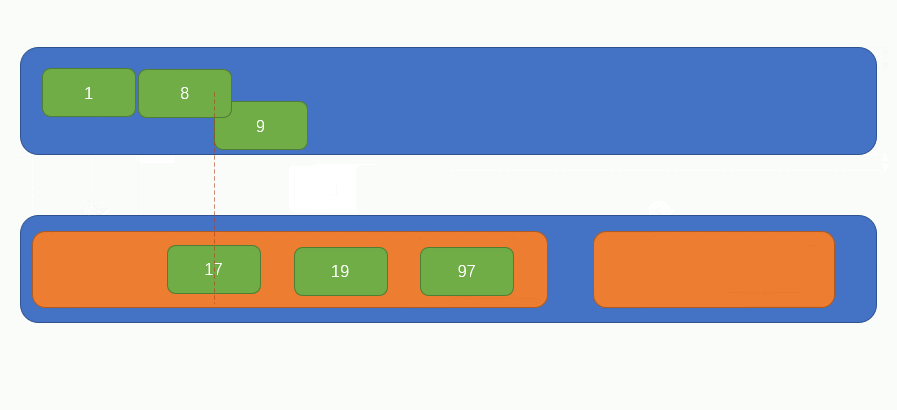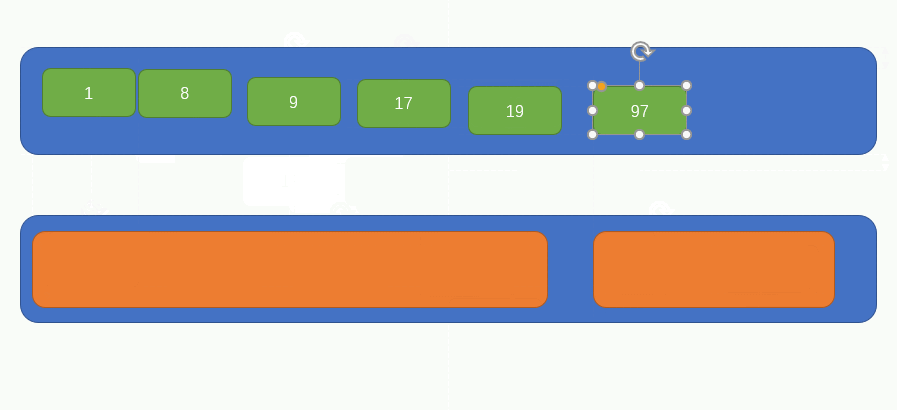
This is a complete merging and sorting process. Next, let's implement it with code

function mergeSort(arr) {

    

    // Combine all elements in pairs until all elements are combined into a group

    while(arr.length > 1){

        // Get the array length before traversal to facilitate the following judgment. It needs to be combined several times

        let length = arr.length

        

        // Create an empty new array to hold all combined elements

        let next_arr = []

        

        // Take two elements for combination, and take length / 2 times in total

        for(let i = 0; i < Math.floor(length / 2); i++){

            // Take out the first element

            let left = [].concat(arr.shift())

            // Take out the second element

            let right = [].concat(arr.shift())

            // Create another new empty array to hold all the combined elements

            let new_arr = []



            // Take the smallest value of the two arrays and put it into the new array until one array is empty

            while(left.length > 0 && right.length > 0){

                let min = left[0] > right[0]? right.shift() : left.shift()

                new_arr.push(min)

            }

            // Add the merged array to the new array

            next_arr.push(new_arr.concat(left.length == 0? right : left))

        }

        // Determines whether there is an ungrouped array

        if(arr.length == 1) next_arr.push(arr[0]);

        

        // Take the new array composed of all combined elements as the object to be traversed next time

        arr = next_arr

    }



    // Returns a complete ordered array

    return arr[0]

}

Let's use this method to see if it is correct. In order to facilitate everyone's understanding, I added a printed code to the merge sorting function to see the array after each traversal. The results are as follows

let arr = [19, 97, 9, 17, 1, 8]

mergeSort(arr)



/* Print results:

After the first combination: [[19, 97], [9, 17], [1, 8]]

After the second combination: [[9, 17, 19, 97], [1, 8]]

After the third combination: [[1, 8, 9, 17, 19, 97]]

*/

Looking at the code, it is not difficult to find that merge sorting takes up a lot of memory, because in the process of combination, we constantly create new arrays and then merge them. However, the comparison times are very few, and the comparison is only carried out every time the elements are merged, so the efficiency of merging and sorting is still very high.

[](

)3, Quick sort

===============================================================

I believe you must be familiar with quick sorting. Even if you haven't used it, you must have heard of it. With such a great reputation, its sorting efficiency must be very high. And quick sorting is often asked in the interview, which may make you write on the spot ~ so we must master its core idea

Quick sort also uses the idea of divide and rule, and its implementation idea is very interesting:

1. First select an element as the base point pivot

2. Put all values smaller than pivot in other elements to the left of pivot; Place all values larger than pivot to the right of pivot

3. Then, all elements on the left and right of pivot are sorted from step 1 until all elements are complete and orderly

The idea looks very simple. Let's take a concrete look at the whole process of quick sorting with an example

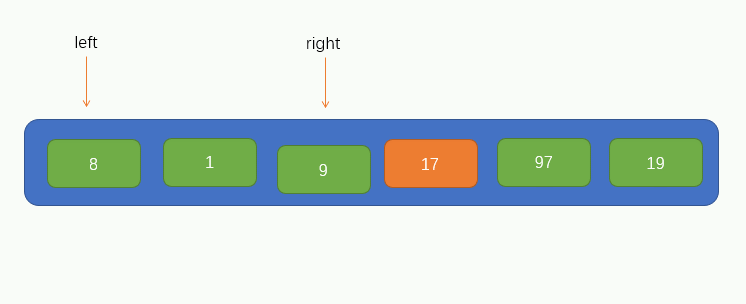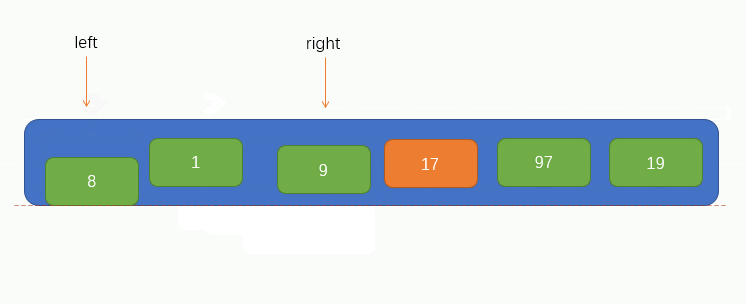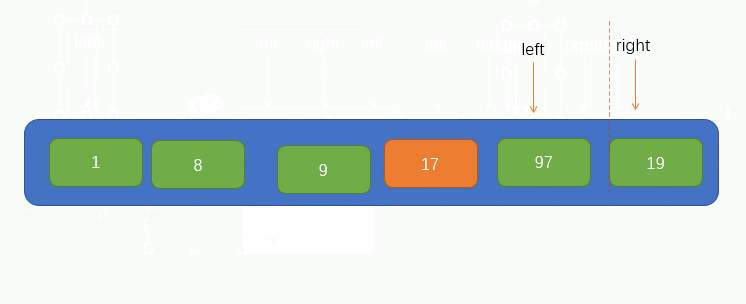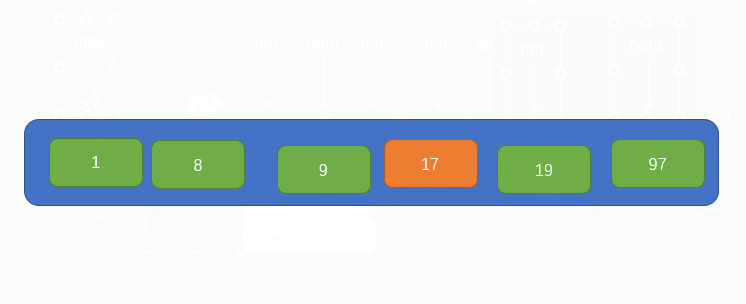
First, there is such a set of data, as shown in the following figure:

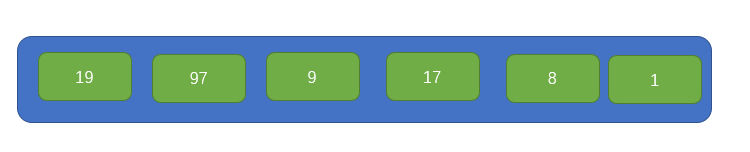
First, we need to select an element as the base point pivot. Finally, after sorting, all the elements on the left of the pivot are smaller than the pivot, and all the elements on the right are larger than the pivot. Therefore, we want to average the two sides as much as possible. Therefore, we will use a way to find an approximate midpoint, that is, take the indexes at both ends of the array, which are left and right respectively, Take another midpoint center, and the result is as follows:

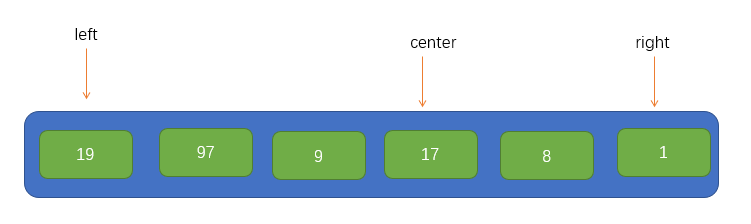
Then find a medium-sized value in these three elements and put it at the beginning of the array, as shown in the following figure:

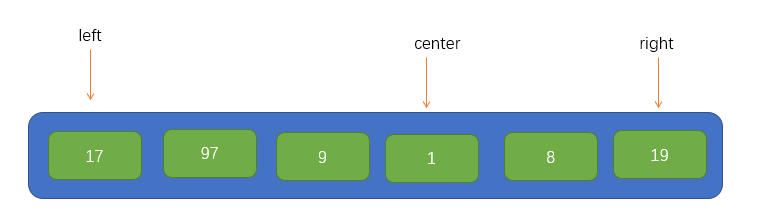
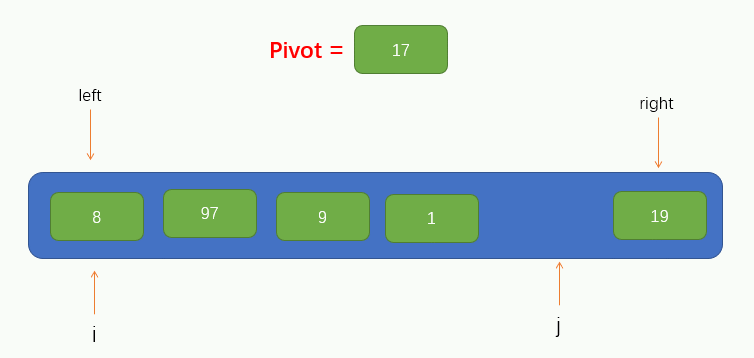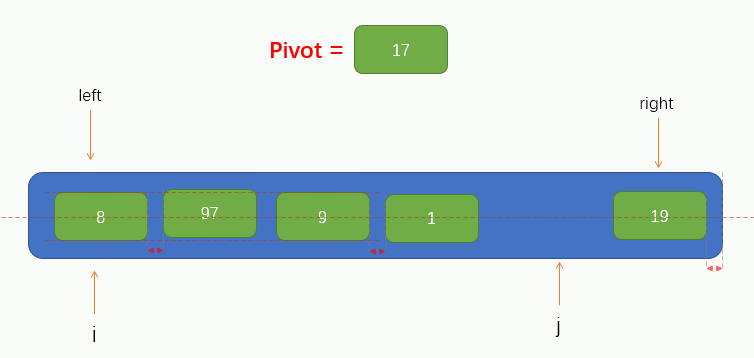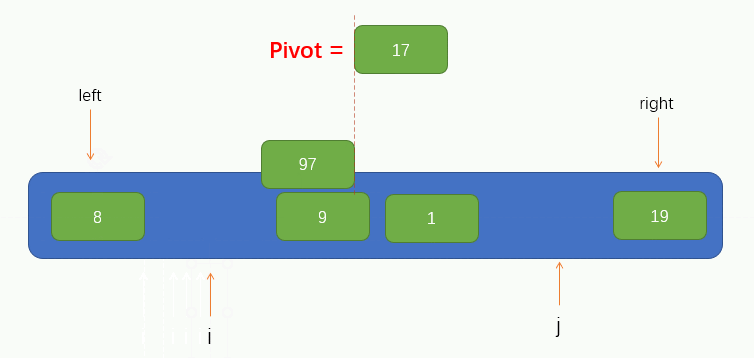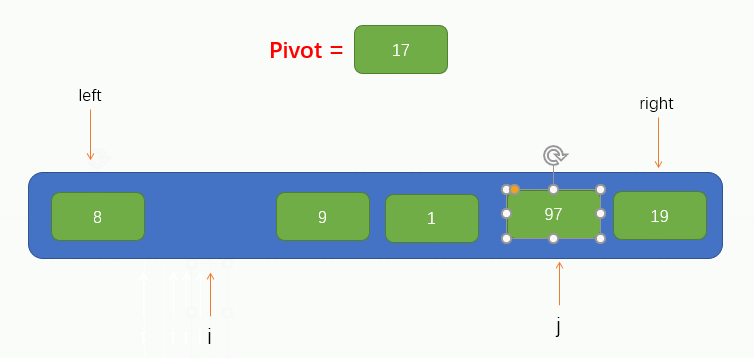
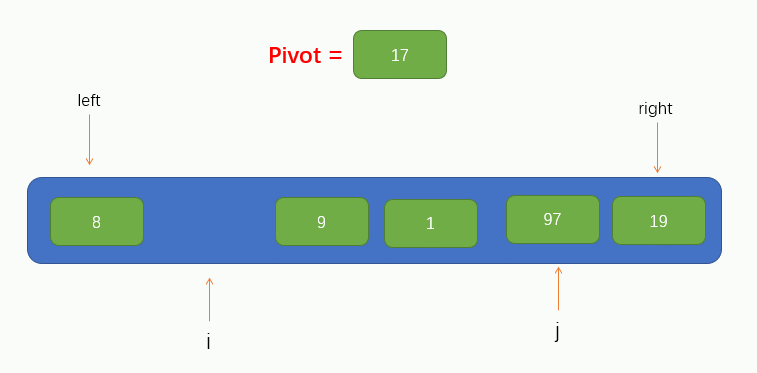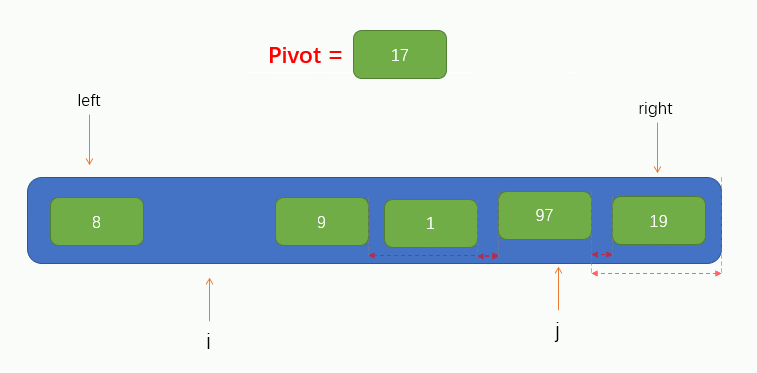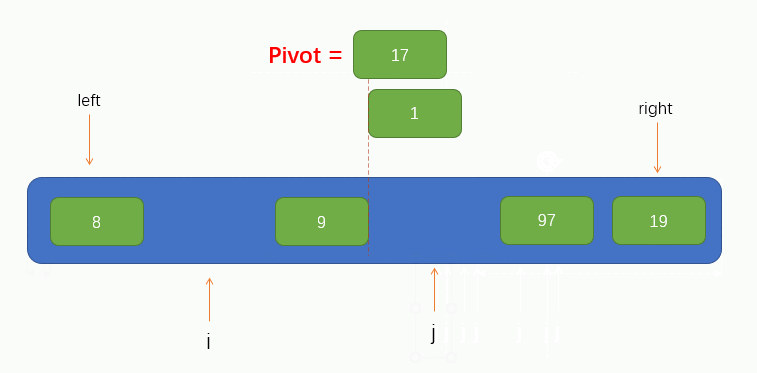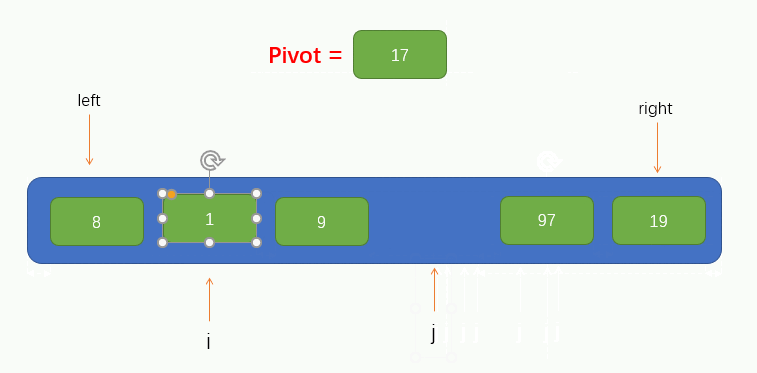
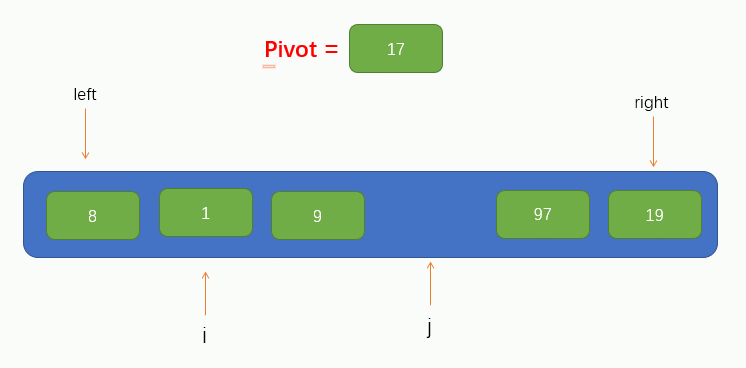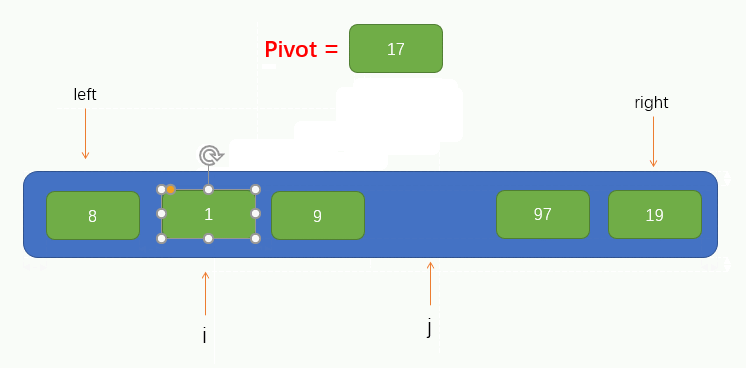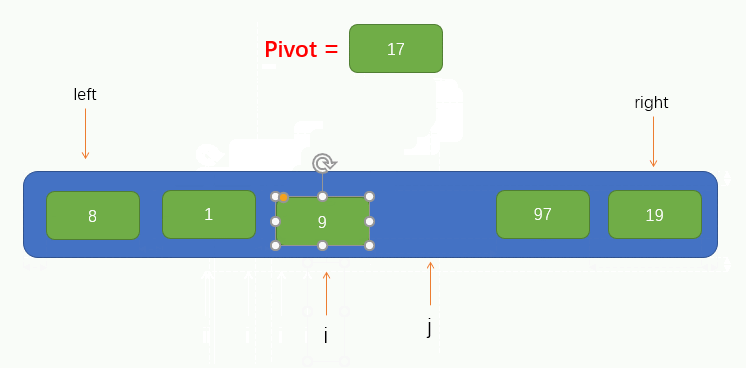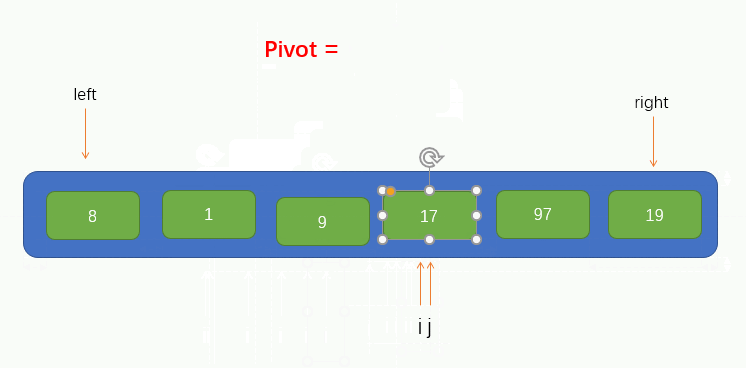
At this point, we can take the first element of the array as the base point pivot of this traversal. At the same time, we will introduce two pointers, i and j, pointing to left and right respectively, as shown in the figure

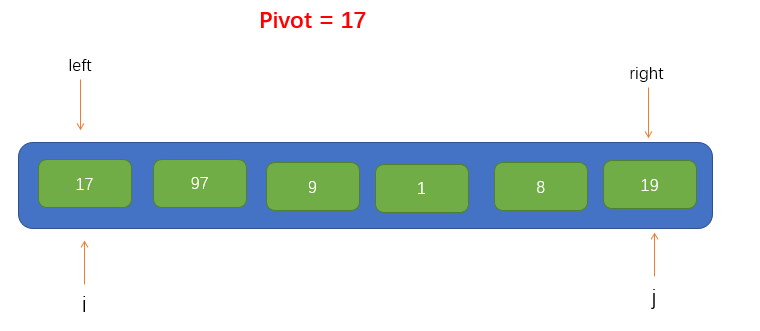
Next, we can traverse. Here, we call the traversal process pit filling method, because now we have taken the first value of the array as pivot, so we can assume that there are no elements at this position, leaving a pit, and we need to fill in other elements. Therefore, we should start from pointer j to the right to find a value smaller than pivot. If it is found, fill the found value into the pit. However, it should be noted that pointer j cannot find the left of pointer i, that is, it stops moving when pointer j coincides with pointer i.

The process is shown in the figure below:

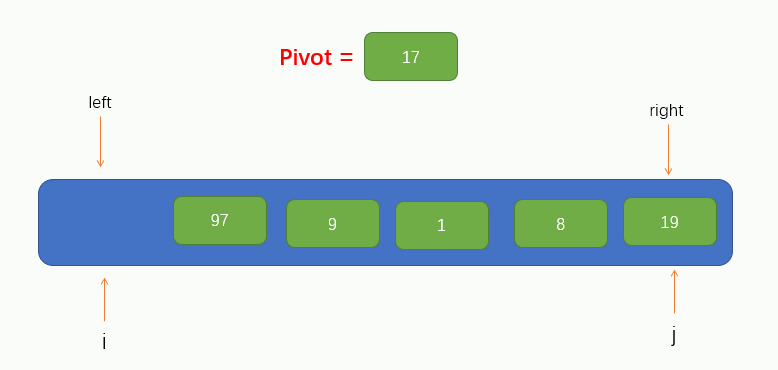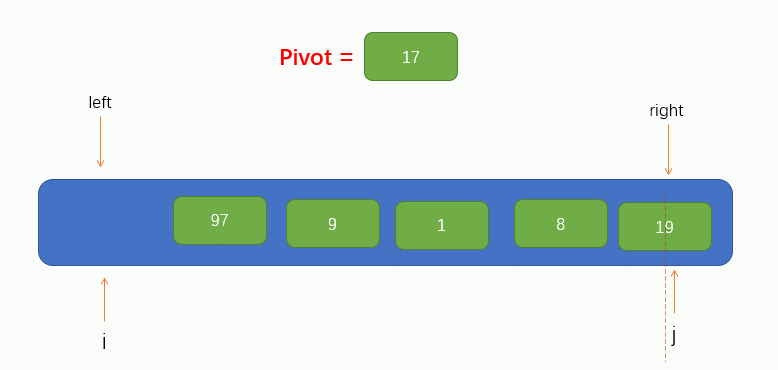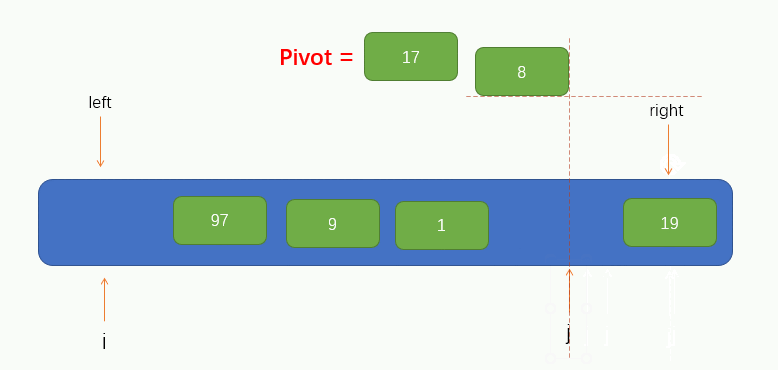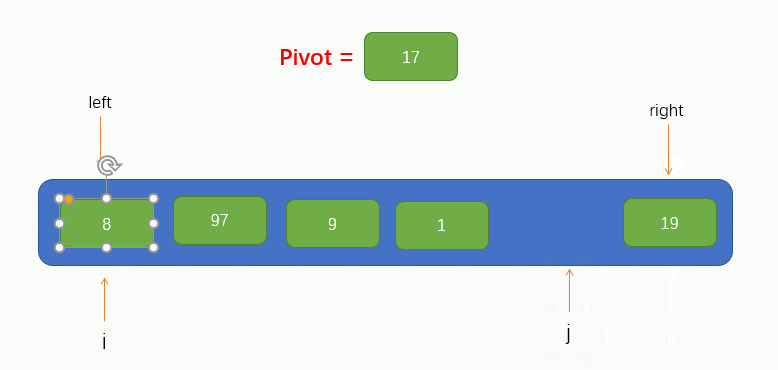
At this time, we can see that the pointer j finds a value 8 less than pivot and fills the found value into the pit. At this time, a pit is left at the position pointed by the pointer j, and other elements are needed to fill the pit. Therefore, we need to make the pointer i find a value greater than pivot to the right and fill the value into the pit. Similarly, Pointer i cannot find the right side of pointer j, that is, it stops moving when pointer i coincides with pointer j.

The process is shown in the figure below:

Pointer i finds a value 97 greater than pivot and fills it into the pit. At this time, a pit is left at the position where pointer i is located. Therefore, we want pointer j to find a value less than pivot to the left and fill it into the pit. The process is shown in the figure:

Then, the pointer i has to find a value greater than pivot to the right, but it is not found after moving two positions, and at this time, the pointer i and pointer j coincide. At this time, we only need to fill the pivot into the pit to realize that all elements on the left of the pivot are smaller than it, and all elements on the right are larger than it, as shown in the figure:

The next operation is to perform the above series of operations on all elements on the left and all elements on the right of the pivot, so as to realize quick sorting. In this example, the number of elements in the left and right areas is less than or equal to 3, so it is convenient to directly compare these values with each other. The process is as follows:

After understanding the implementation idea of quick sort, let's implement it with code

function quickSort(arr) {

    // Two data are exchanged

    function exchange(v1, v2) {

        let temp = arr[v1]

        arr[v1] = arr[v2]

        arr[v2] = temp

    }

    

    // Find a relatively suitable element and put it at the position where the array index is 0 as the base point pivot

    function init(left, right) {

        let center = Math.floor((left + right) / 2)



        // Compare the sizes of the left, center and right indexes from small to large

        if(arr[left] > arr[right]) exchange(left, right)

        if(arr[center] > arr[right]) exchange(center, right)

        if(arr[left] > arr[center]) exchange(left, center)



        // Judge whether the array length is greater than 3. If it is less than 3, the array has been sorted and no processing is required

        if(right - left > 2) exchange(left, center)

    }



    function quick(left, right) {

        init(left, right)

        // If the array length is less than or equal to 2, there is no need to do anything, because the init function has been sorted

        if(right - left <= 2) return;

        

        // Create pointers i and j to left and right, respectively

        let i = left

        let j = right

        // Take the first element of the array area as the base point pivot

        let pivot = arr[i]



        // Continuously let the pointers i and j find the appropriate value to fill the pit until the two pointers coincide

        while(i < j) {

            // Pointer j keeps looking to the left for a value less than pivot, but pointer j cannot find the left of pointer i

            while(arr[j] > pivot && j > i) {

                j --

            }

            // Fill the found value less than pivot into the pit pointed to by pointer i

            arr[i] = arr[j]



            // Pointer i keeps looking to the right for a value greater than pivot, but pointer i cannot find the right of pointer j

            while(arr[i] < pivot && i < j) {

                i ++

            }

            // Fill the found value greater than pivot into the pit pointed by pointer j

            arr[j] = arr[i]

        }



        // Fill the pivot into the pit where pointer i and pointer j point together

        arr[i] = pivot



        // Quickly arrange all elements on the left of pivot at this time

        quick(left, i - 1)