Data structure and algorithm learning note tree

Data structure and algorithm learning notes (7) tree

Previous review

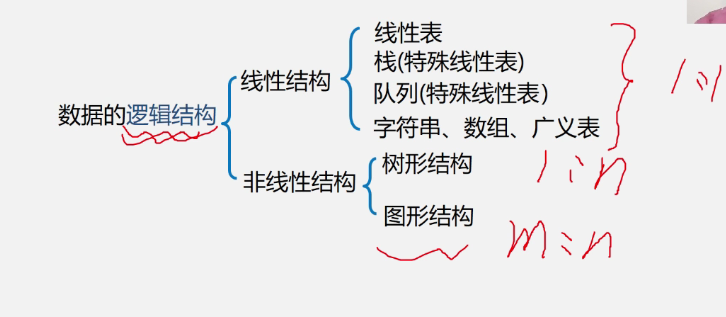
1, Definition of tree and binary tree

1. Trees

Definition of tree

Recursive nested definition

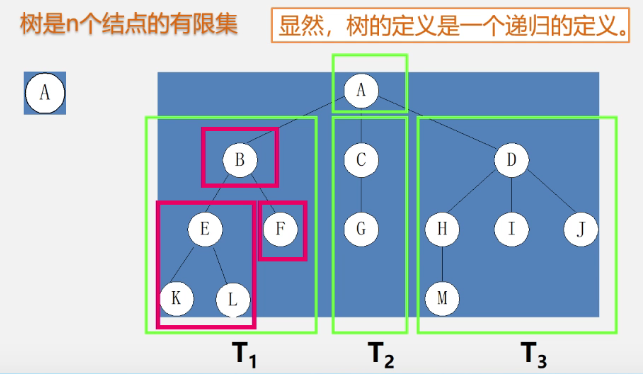
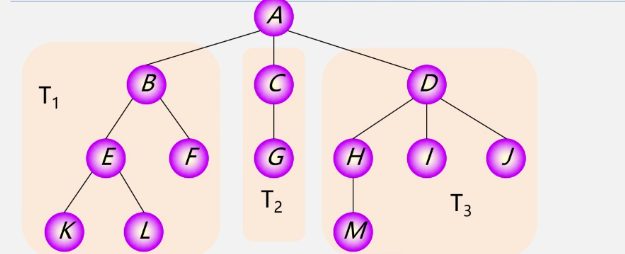
Other representations of trees

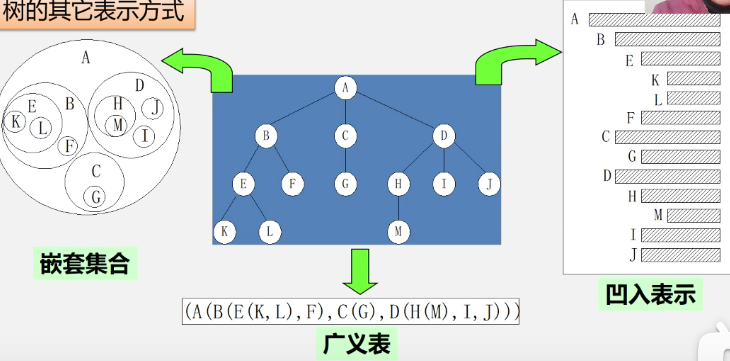
It's a bit like this markdown syntax:

A
B
- E
  - K
  - L
- F
C
- G
D
- H
  - M
- I
- J

Basic terms of trees

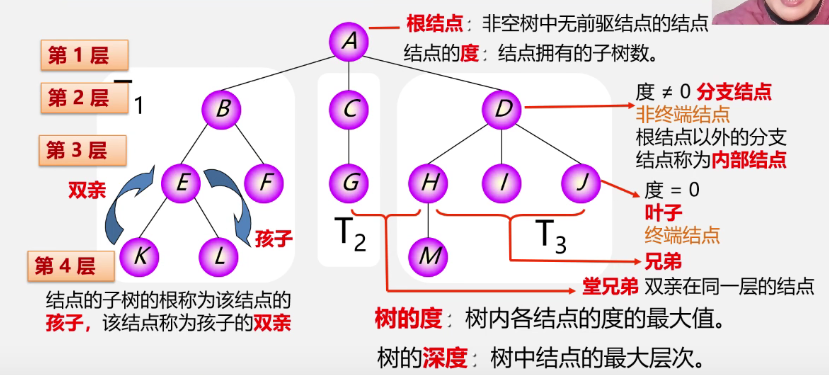
The degree of a node is also the number of branches and the number of successors

- Ordered tree: the subtrees of nodes in the tree are ordered from left to right (the leftmost is the first child)
- Unordered tree: the subtrees of the nodes in the tree have no order
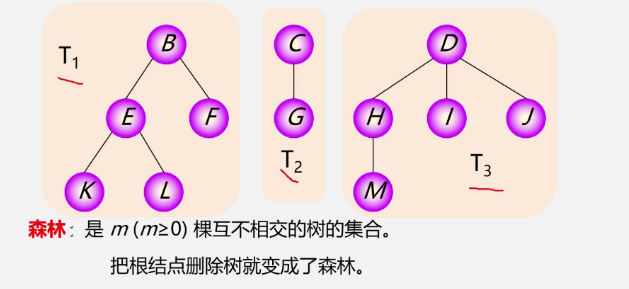
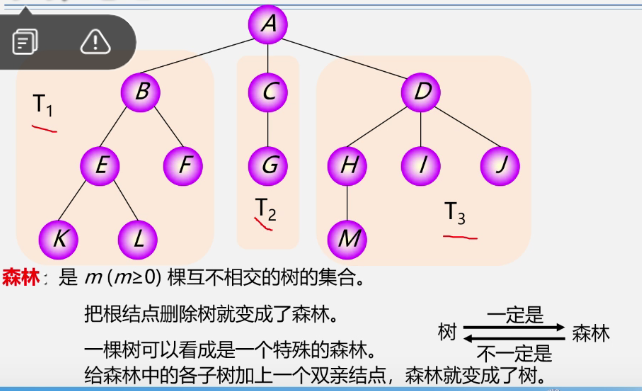
- Forest: a collection of m(m ≥ 0) disjoint trees
  
  Tree to forest:

Comparison between tree structure and linear structure

2. Binary tree

Definition of binary tree

The difference between binary tree and tree

Binary tree and tree are two concepts. Binary tree is not a special case of tree

example
Although they are two concepts, the basic terms related to trees are applicable to binary trees

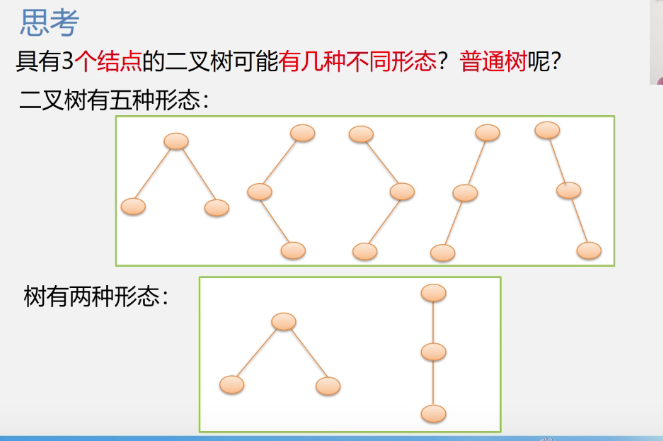
Basic form of binary tree

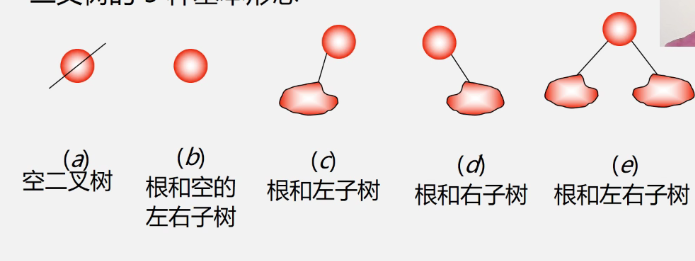
3. Abstract data type definition of tree and binary tree

Tree:

Mainly learn the abstract data type definition of binary tree
- There are many basic operations. The following are the main ones:

2, Properties and storage structure of binary tree

1. Properties of binary tree

① Binary tree properties 1, 2, 3

Number of nodes per layer
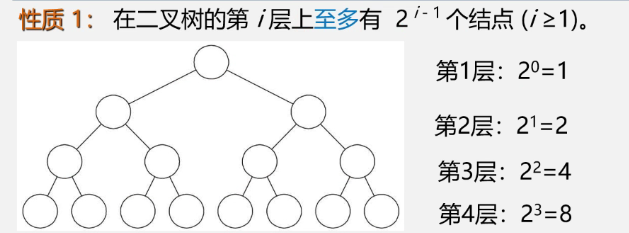
- There is at least one node on layer i
Total number of nodes
Relationship between the number of leaves and the number of nodes with degree 2

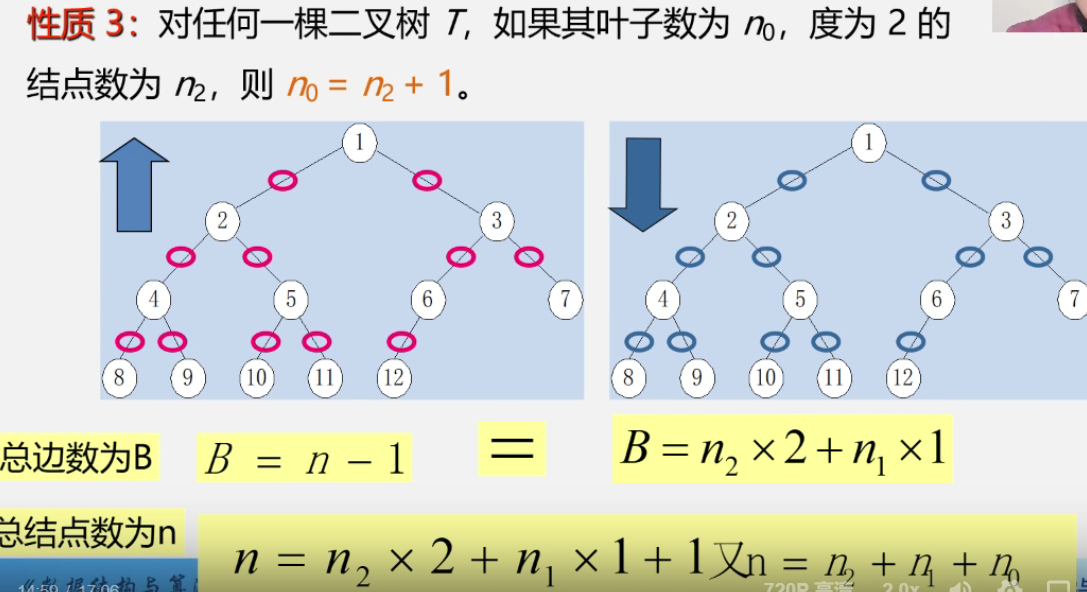
n represents the total number of nodes

n 1 n_1 n1 represents a node with a degree of 1
- 🤩 Top down and then bottom up thinking

② Two special forms of binary trees: full binary tree and complete binary tree

Definition and characteristics

Full binary tree

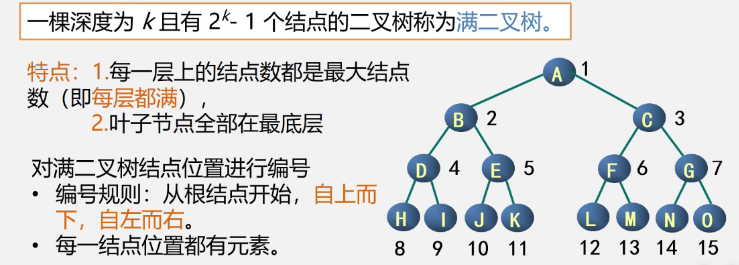
Complete binary tree
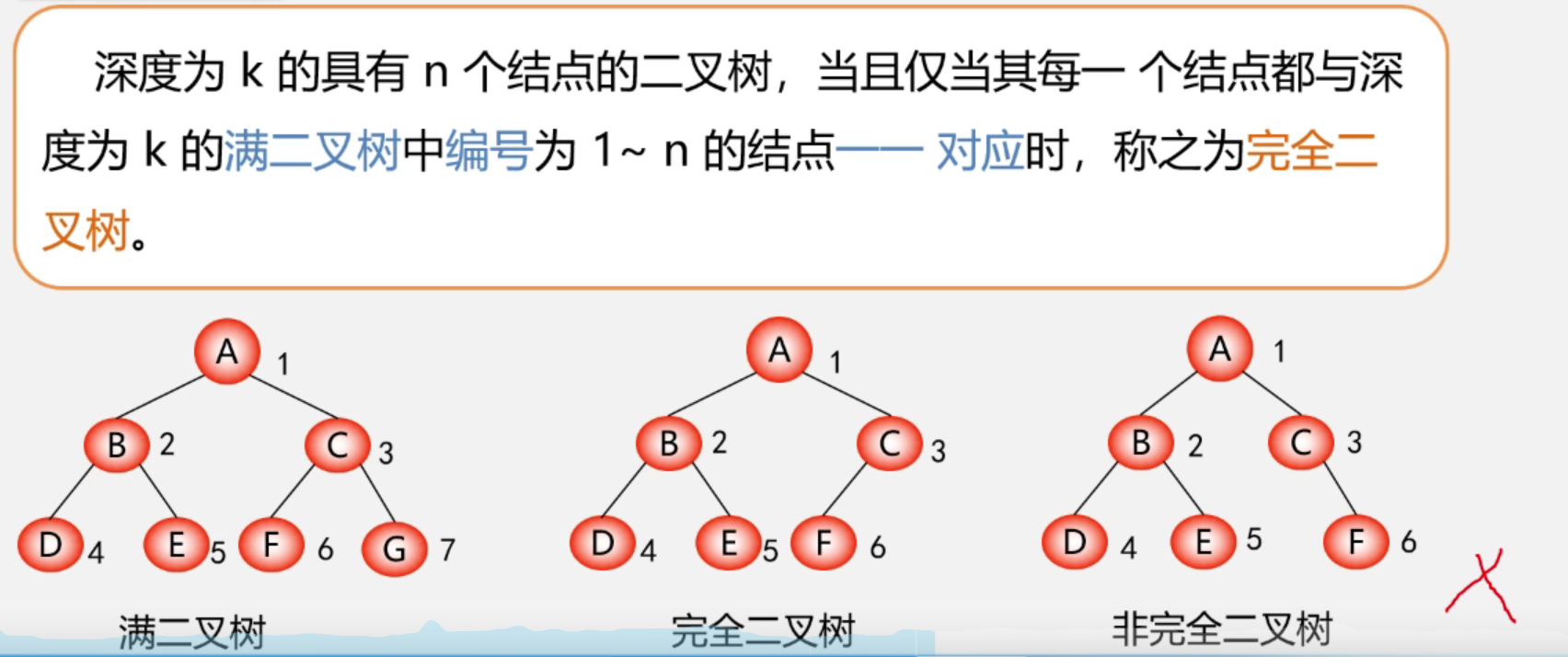
- Judgment skills
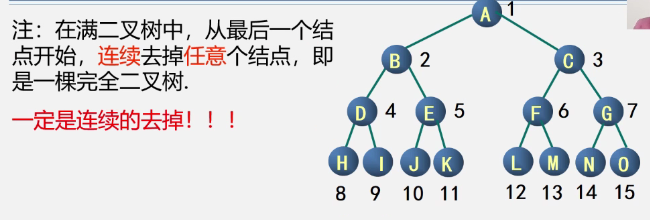
- characteristic
[external chain picture transfer failed. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-qtpivbor-1637761025234)( https://cdn.jsdelivr.net/gh/xin007-kong/picture_new/img/20210928093038.png )]

Relationship between the two

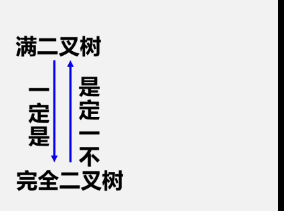
③ Properties 4 and 5 of binary tree (two properties of complete binary tree)

Property 4: depth of complete binary tree

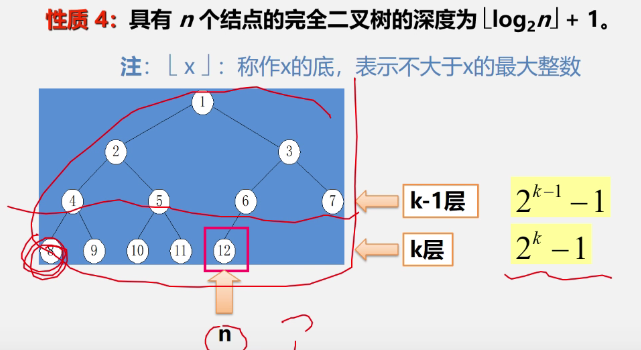
Property 5: relationship between node numbers
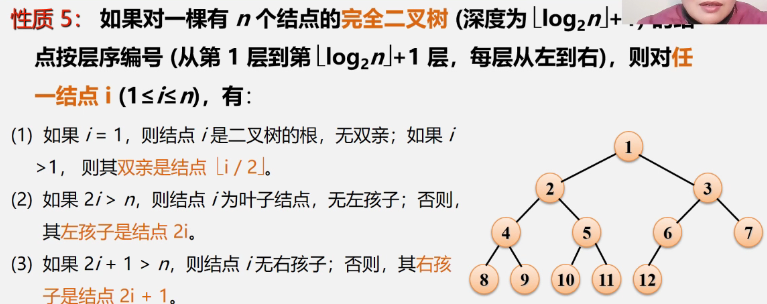
- Property 5 shows the relationship between parent node numbers and child node numbers in a complete binary tree
  
  Proof: mathematical induction

Judge complete binary tree: with the help of queue

https://www.bilibili.com/video/BV1QP4y1h7qH?from=search&seid=13048496972823229128&spm_id_from=333.337.0.0

2. Storage structure of binary tree

[external link picture transfer failed. The source station may have anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-lwsp7ijn-1637761025237)( https://cdn.jsdelivr.net/gh/xin007-kong/picture_new/img/20211005081221.png )]

① Sequential storage

Implementation: according to the node level number of the full binary tree, the data elements in the binary tree are stored in turn
For example:

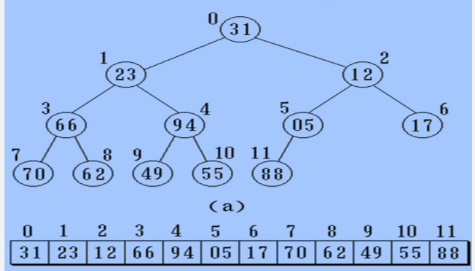
First from top to bottom, then from left to right
type definition
```
#define MAXTSIZE 100
typedef TElemType SqBiTree[MAXTSIZE];
SqBiTree bt;
```
The above SqBiTree is a data type, and the defined variable type is texttype [maxsize]

That is, the bt above is an array of texttype with maxsize elements
Look at an example
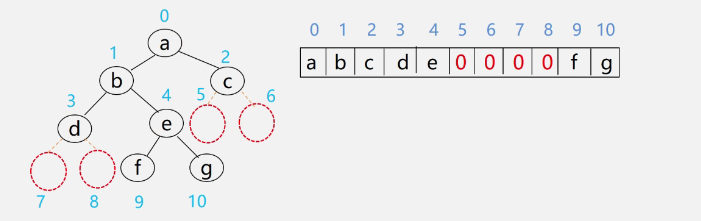
Characteristics of binary tree sequential storage

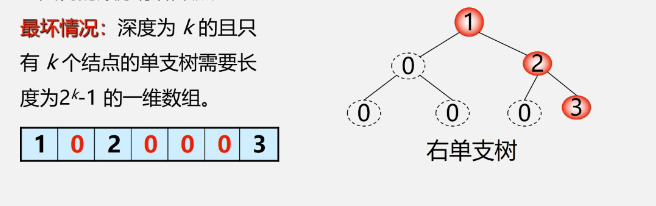
② Chain storage

Binary linked list

Characteristics of binary tree nodes

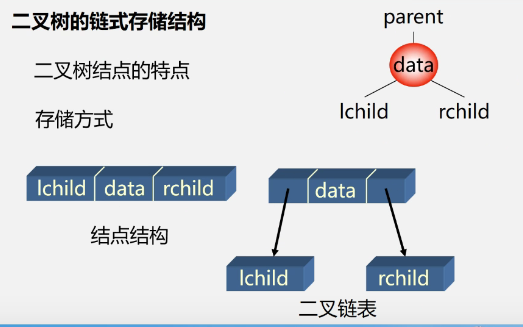
Storage structure definition

typedef struct BiNode{
	TElemType	data;
	struct BiNode	*lchild,*rchild;	//Left and right child pointers
}BiNode,*BiTree;

Look at an example

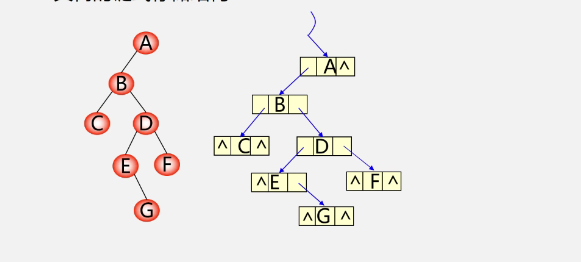
Number of empty finger fields
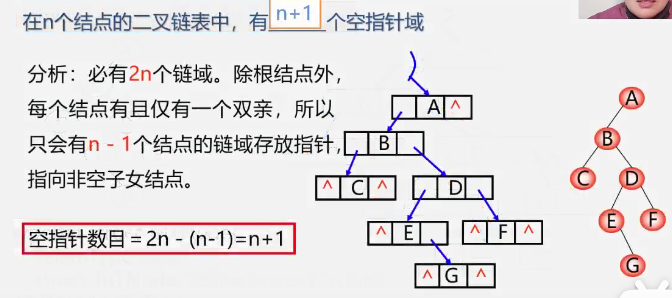
- Each node has a connection to its parents, except the root node
  - Therefore, only the chain domain of n-1 nodes will store pointers to non empty child nodes

Trigeminal linked list

Sometimes you need to find a precursor

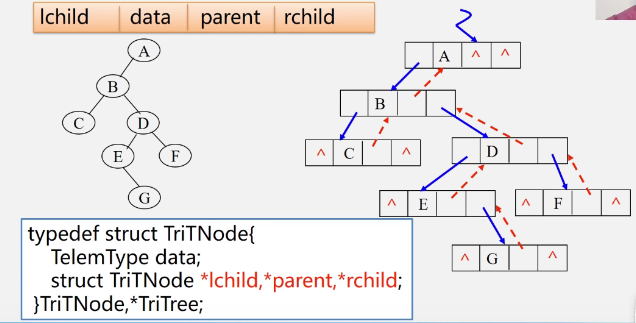
3, Traversing binary tree and clue binary tree

1. Overview of traversal method

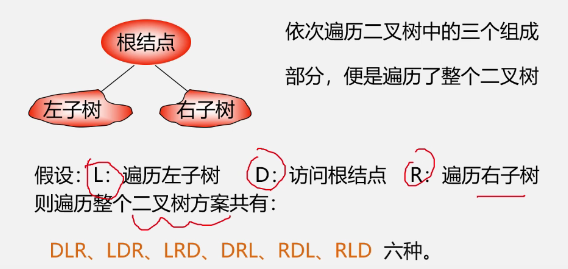
Focus on DLR, LDR and LRD

According to the recursive definition of binary tree, traversing left subtree and right subtree can be "recursive" as traversing binary tree

Operation definition of preordered traversal of binary tree

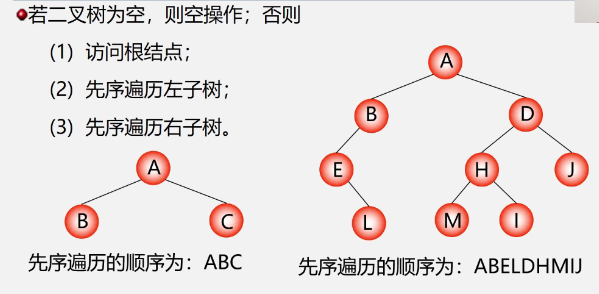
Operation definition of traversing binary tree in middle order

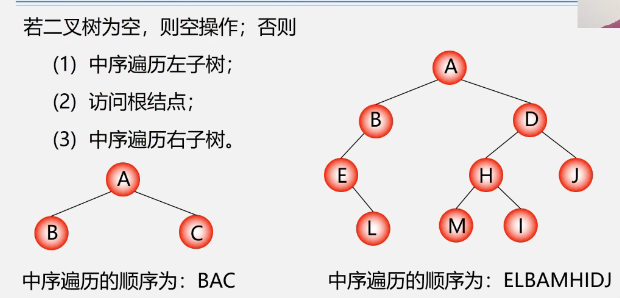
Operation definition of post order traversal of binary tree

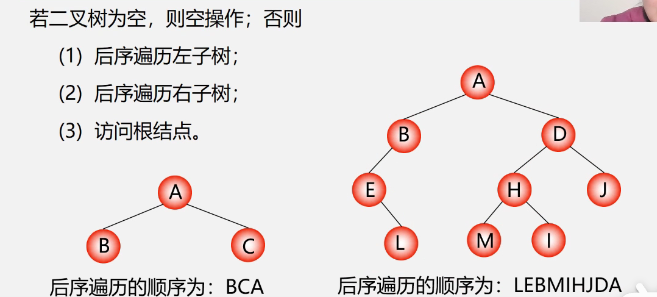
example

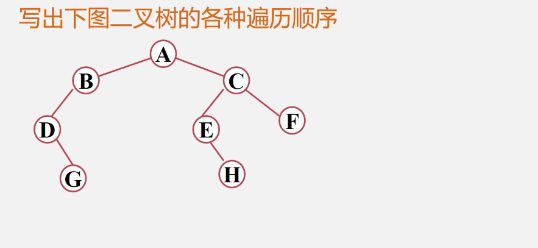
Preamble: ABDGCEHF
Middle order: DGBAEHCF
Later: GDBHEFCA

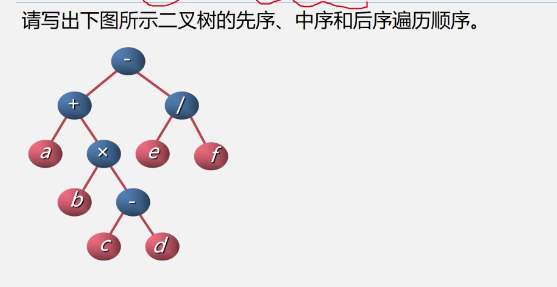
Precedence: - + a × b-cd/ef
Middle order: a+b × c-d-e/f
Later: abcd- ×+ ef/-

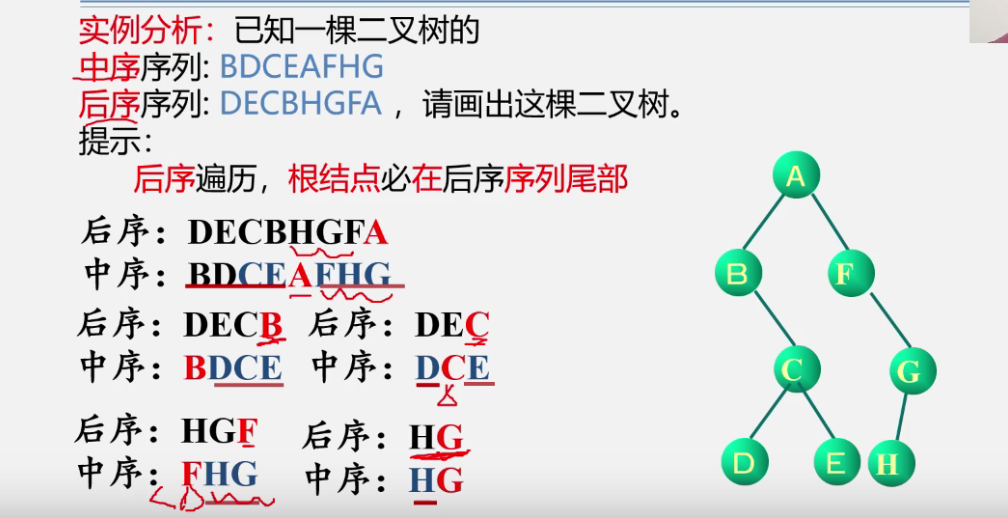
2. Determine the binary tree according to the traversal sequence

If the values of each node in the binary tree are different, the pre order sequence, middle order sequence and post order sequence of binary tree nodes are unique
The unique binary tree can be determined by the pre order sequence and middle order sequence of the binary tree, or by the post order sequence and middle order sequence of the binary tree
- example
  
  [the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (IMG hgendyck-163776102558)( https://cdn.jsdelivr.net/gh/xin007-kong/picture_new/img/20211005094048.png )]
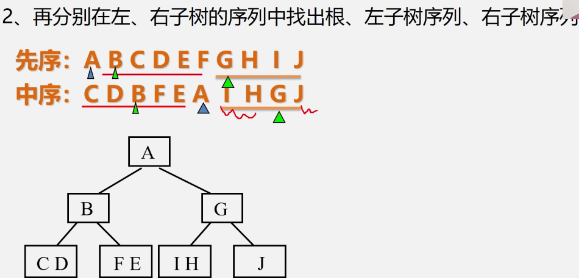
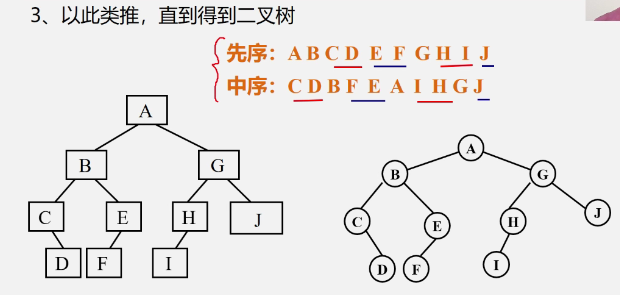
- example

3. Implementation of traversal method of binary tree

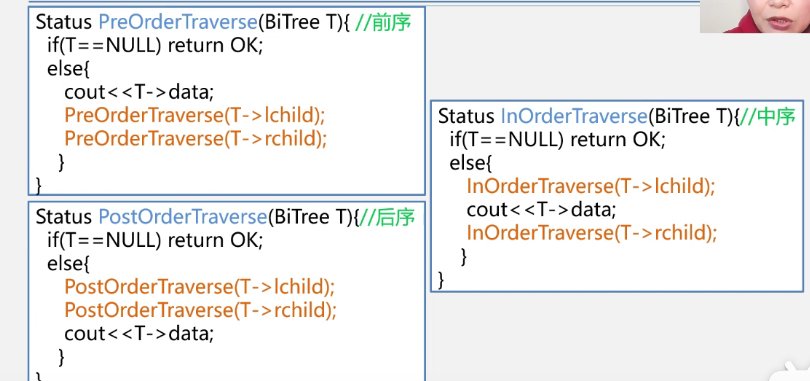
Preorder traversal recursive algorithm

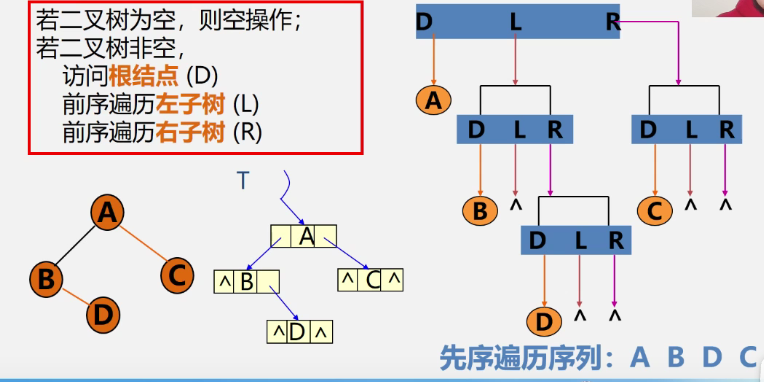
Status PreOrderTraverse(BiTree T){
	if(T==NULL)	return OK;	//Empty binary tree
	else{
		visit(T);	//Access root node
		PreOrderTraverse(T->lchild);	//Recursive traversal of left subtree
		PreOrderTraverse(T->rchild);	//Recursive traversal of right subtree
	}
}

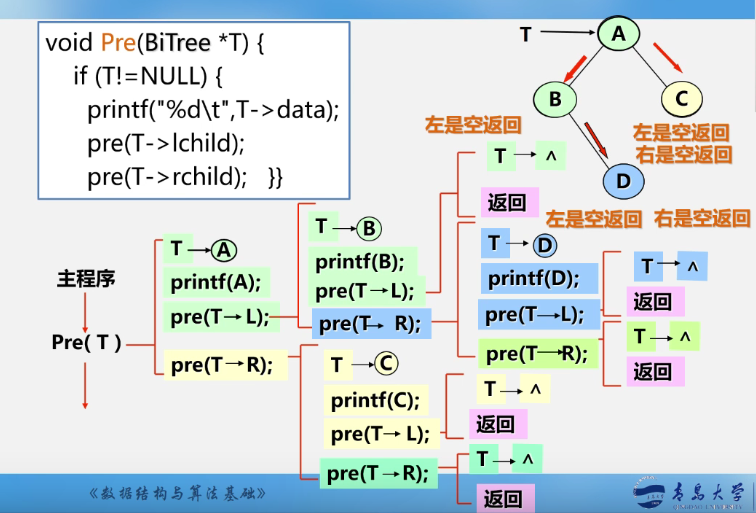
Preorder sequence

ABDC

Middle order traversal recursive algorithm

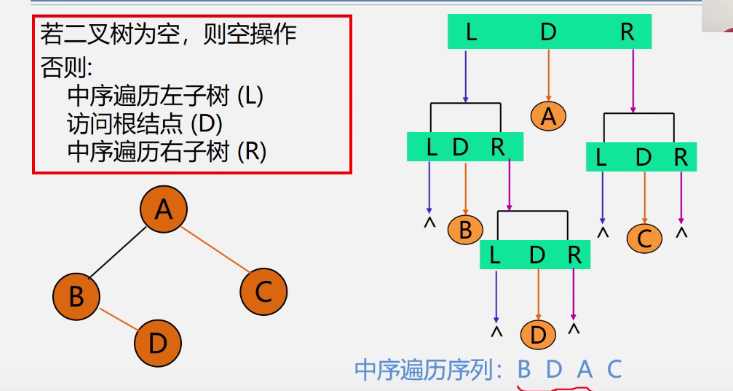
Status InOrderTraverse(BiTree T){
	if(T==NULL)	return OK;	//Empty binary tree
	else{
		InOrderTraverse(T->lchild);	//Recursive traversal of left subtree
		visit(T);	//Access root node
		InOrderTraverse(T-rchild);	//Recursive traversal of right subtree
	}
}

Postorder traversal recursive algorithm

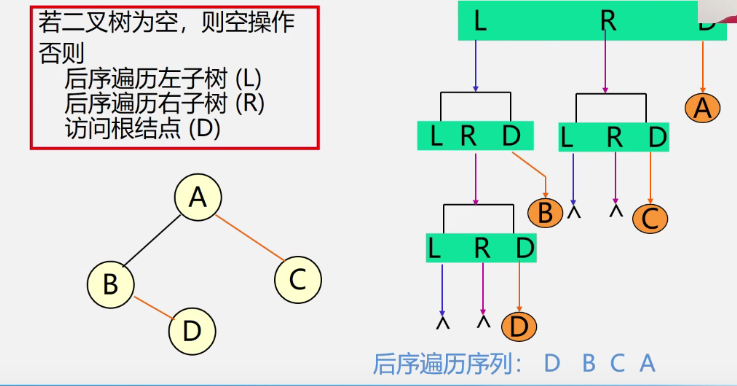
Status PostOrderTraverse(BiTree T){
	if(T==NULL)	return OK;	//Empty binary tree
	else{
		PostOrderTraverse(T->lchild);	//Recursive traversal of left subtree
		PostOrderTraverse(T-rchild);	//Recursive traversal of right subtree
		visit(T);	//Access root node
		
	}
}

Comparative analysis of three recursive traversal algorithms

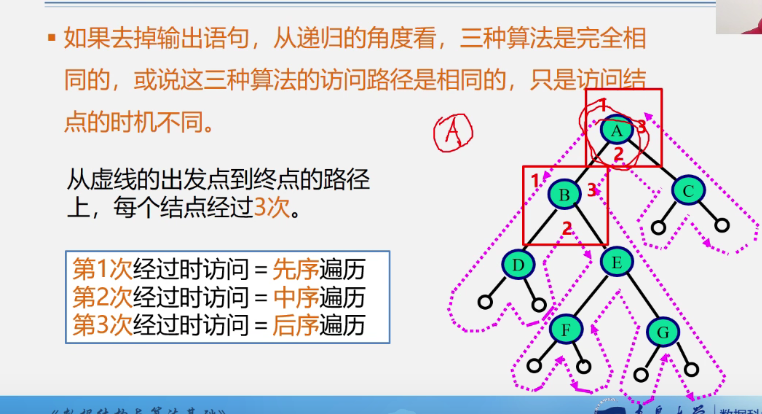
Space is stack

Middle order traversal non recursive algorithm

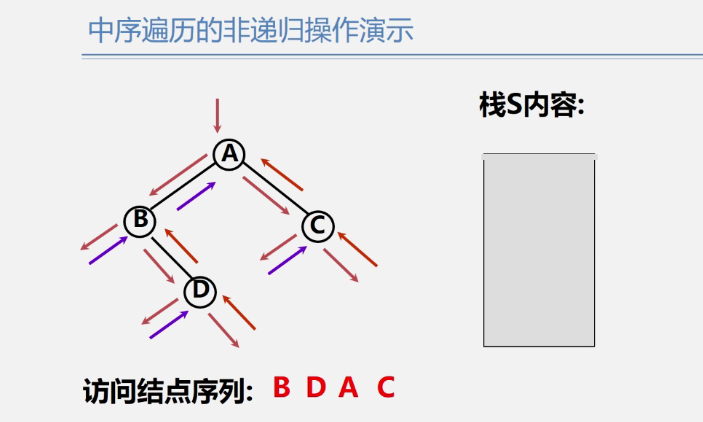
Status InOrderTraverse(BiTree T){
	BiTree p;
	InitStack(S);
	p=T;	//Point to root node
	while(p||!StackEmpty(S)){
		if(p){
			Push(S,p);
			p=p->child;
		}
		else{
			Pop(S,p);
			printf("%c",q->data);
			p=q->child;
		}
		return OK;
	}
}

Hierarchical traversal algorithm of binary tree

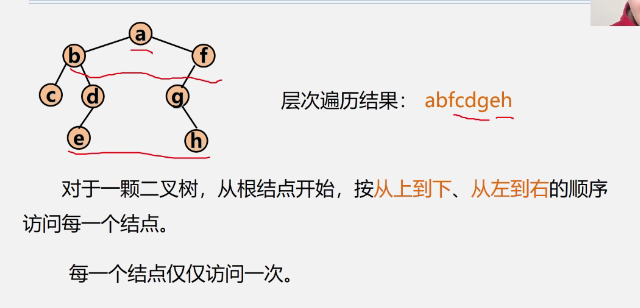
Algorithm idea

Algorithm description

Use sequential loop queue

Queue types are defined as follows:

typedef struct{
	BTNode data[MaxSize];	//Store elements in the queue
	int front, rear;		//Head and tail pointer
}SqQueue;				//Sequential loop queue type

Binary tree hierarchy traversal algorithm:

void LevelOrder(BTNode *b){
	BTNode *p;
	SqQueue *qu;	//Initialize queue
	enQueue(qu,b);	//The root node pointer enters the queue
	while(!QueueEmpty(qu)){		//Loop if the queue is not empty
		deQueue(qu,p);	//Outgoing node p
		printf("%c",p->data);	//Access node p
		if(p->lchild!=NULL)
			enQueue(qu,p->lchild);	//When there are left children, let them join the team
		if(p->rchild!=NULL)
			enQueue(qu,p->rchild);	//When there are right children, let them join the team
	}
}

4. Application of binary tree traversal algorithm

Algorithm for establishing binary tree

The binary linked list of binary tree is established by traversing the sequence in advance

The tree established according to a pre sequence is not unique, such as:

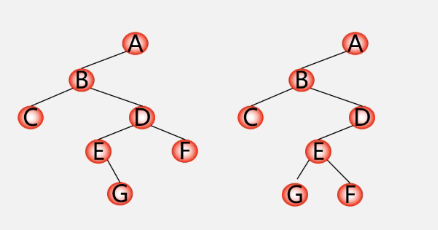
To avoid duplication, you can add empty nodes and use # instead

Algorithm description

Status CreateBiTree(BiTree &T){
	scanf(&ch);
	if(ch=="#") T=NULL;
	else{
		if(!(T=(BiTNode*)malloc(sizeof(BiTNode))))
		{	//T=new BiTNode;
			exit(OVERFLOW);	
		}
        T->data = ch;	//Generate root node
        CreateBiTree(T->lchild);	//Construct left subtree
        CreateBiTree(T->rchild);	//Construct right subtree
	}
    return OK;
}

Duplicate binary tree

Algorithm idea

Algorithm description

int Copy(BiTree T, BiTree &NewT){
	if(T==NULL){	//If it is an empty tree, return 0
		NewT=NULL;
		return 0;
	}
	else{
		NewT=new BiTNode;
		NewT->data=T->data;
		Copy(T->lChild,NewT->lchild);
		Copy(T->rchild,NewT->rchild);
	}
}

Calculate the depth of the binary tree

Algorithmic thought

Algorithm description

int Depth(BiTree T){
	if(T==NULL)	return 0;
	else{
		m=Depth(T->lchild);
		n=Depth(T->rchild);
		if(m>n)	
			return (m+1);
		else 
			return (n+1);
	}
}

Calculate the total number of binary tree nodes

Algorithmic thought

Plus 1 is the root node

Algorithm description

int NodeCount(BiTree T){
	if(T==NULL)
		return 0;
	else
		return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
}

Calculate the number of leaf nodes of binary tree

Algorithmic thought

Algorithm description

int LeafCount(BiTree T){
	if(T==NULL)	//If it is an empty tree, return 0
		return 0;
	if(T->lchild == NULL && T->rchild == NULL)
		return 1;	//If it is a leaf node, return 1
	else
		return LeafCount(T->lchild) + LeafCount(T->rchild);
}

5. Clue binary tree

why
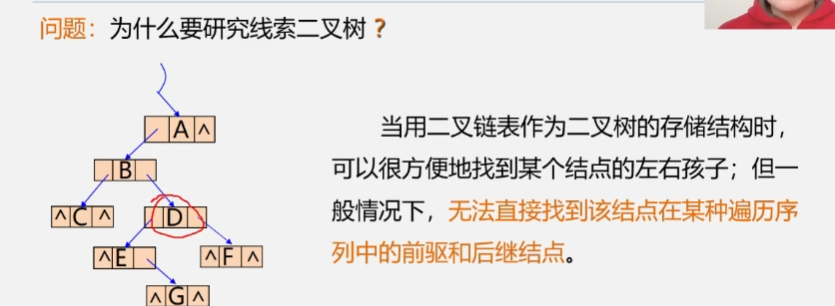
- Possible solutions
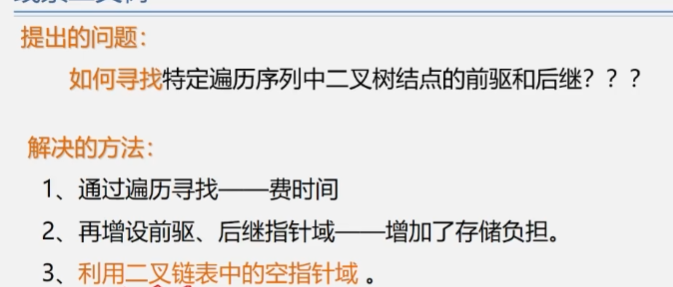
- Review the empty finger field
  
  [external chain picture transfer failed. The source station may have anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-lofyc38f-163776102579)( https://cdn.jsdelivr.net/gh/xin007-kong/picture_new/img/20211008083920.png )]
- Empty finger needle field using binary linked list
what
- The process of turning a binary tree into a clue binary tree in a certain ergodic order is called cueing
- example

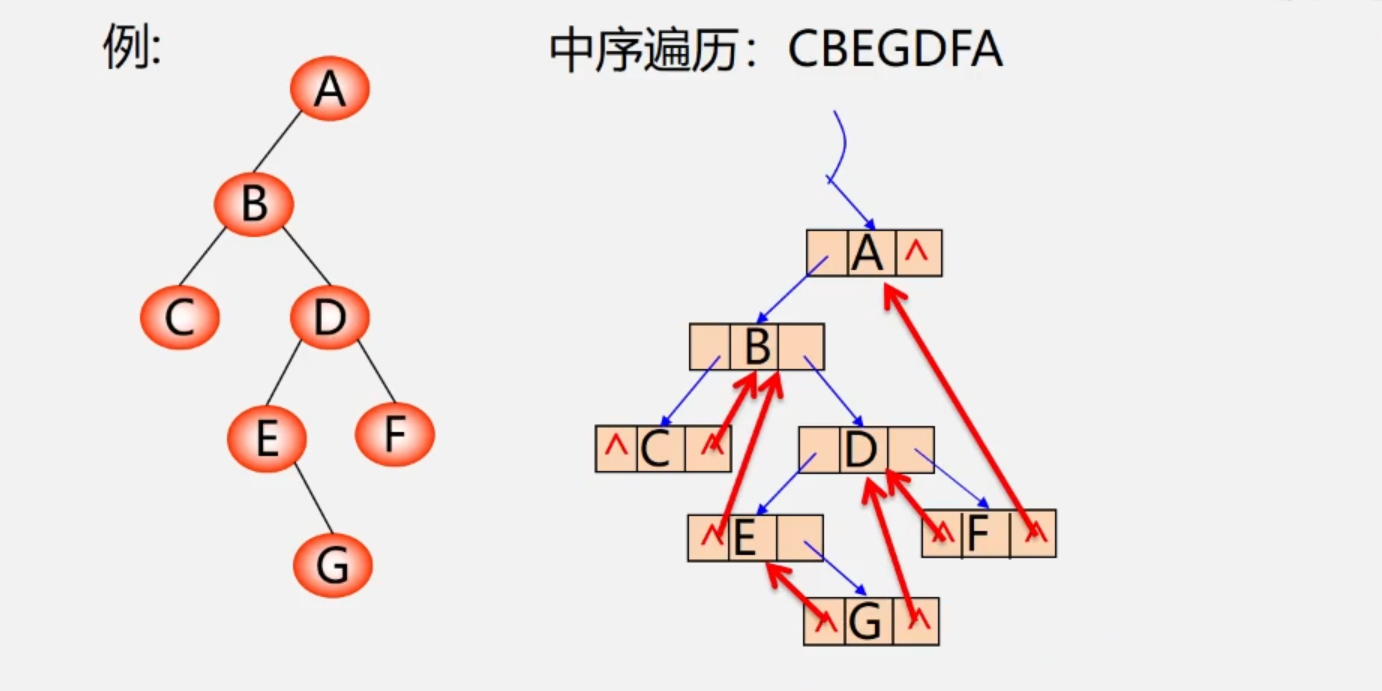
Node structure

typedef struct BiThrNode{
	int data;
	int ltag,rtag;
	struct BiThrNode *lchild,*rchild;
}BiThrNode, *BiThrTree;

Storage of clue binary tree

Preordered clue binary tree

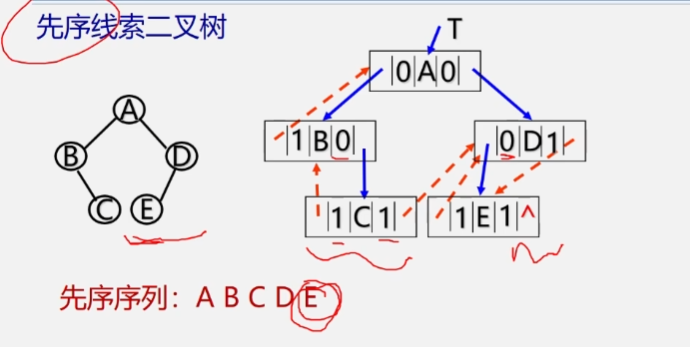
Middle order clue binary tree

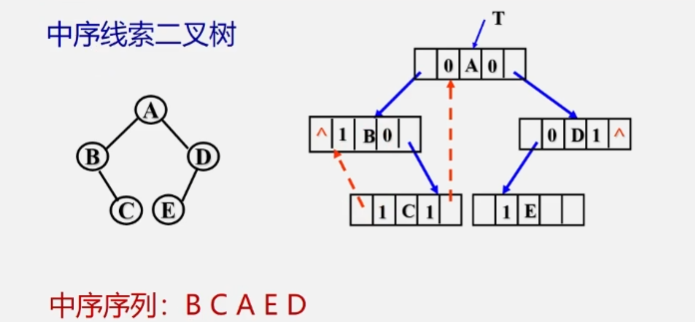
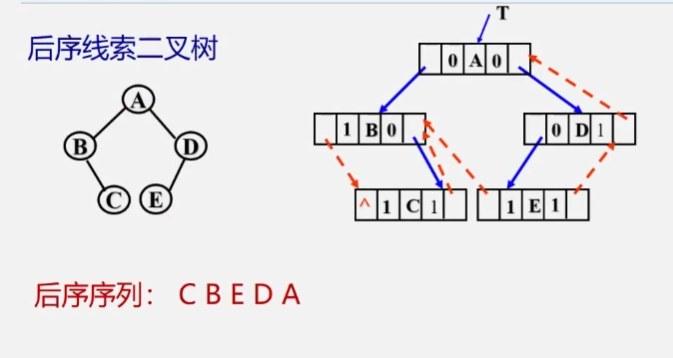
Post ordered clue binary tree

Add head node

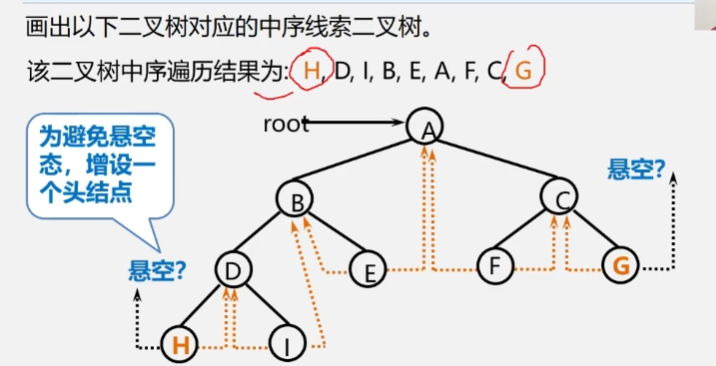
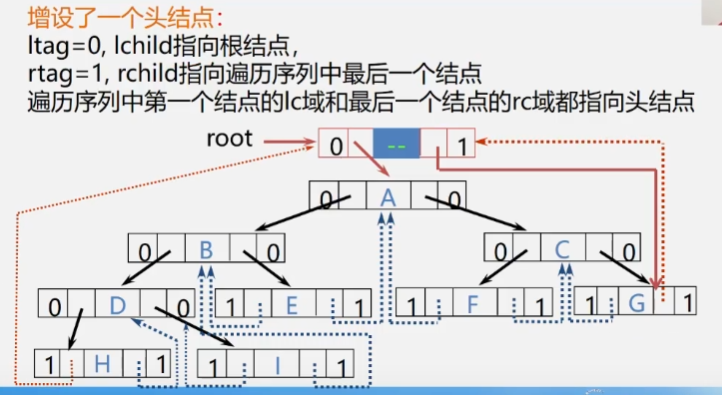
4, Trees and forests

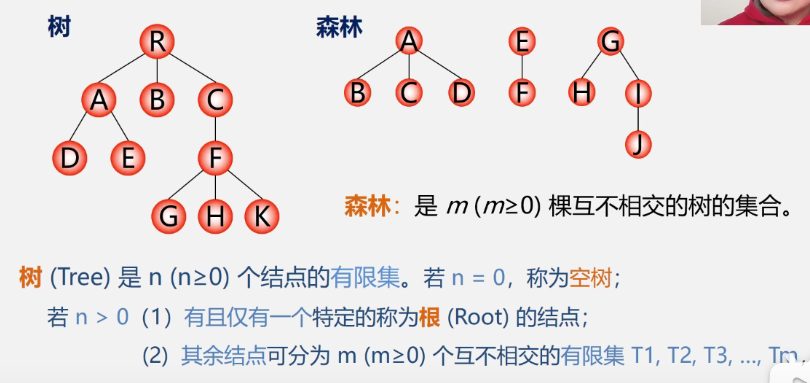
1. Storage structure of tree

Parental representation

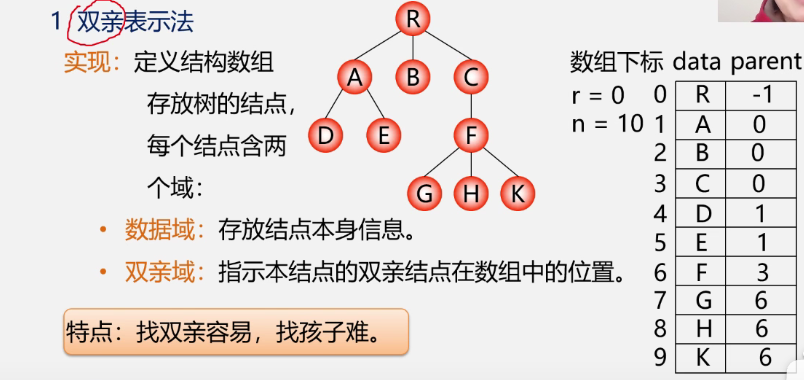
C language type description

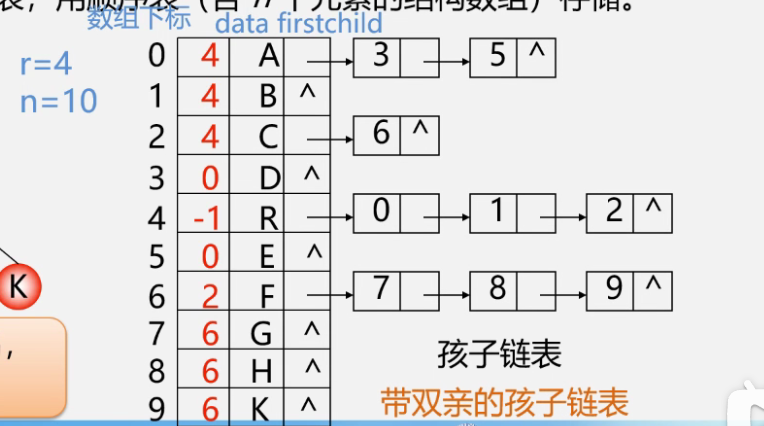
Child list

C language type description
Add more data fields

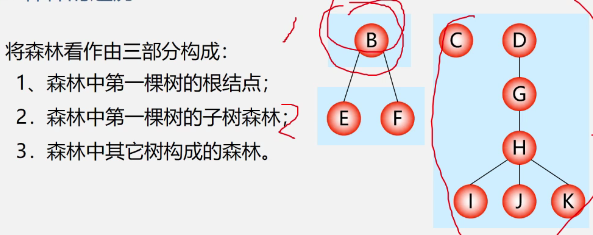
Child brother representation (binary tree representation, binary linked list representation)

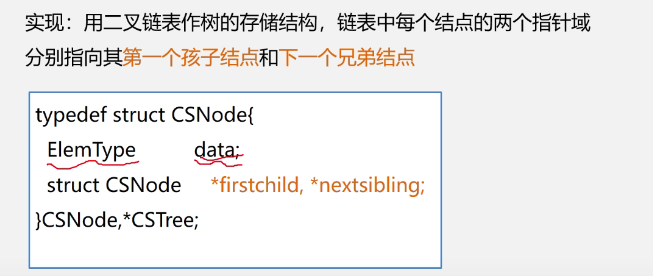
example

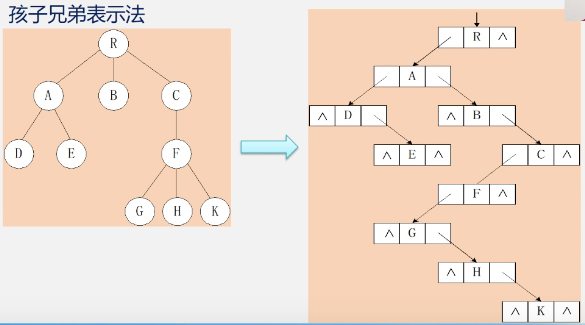
2. Transformation between tree and binary tree

Tree to binary tree

example
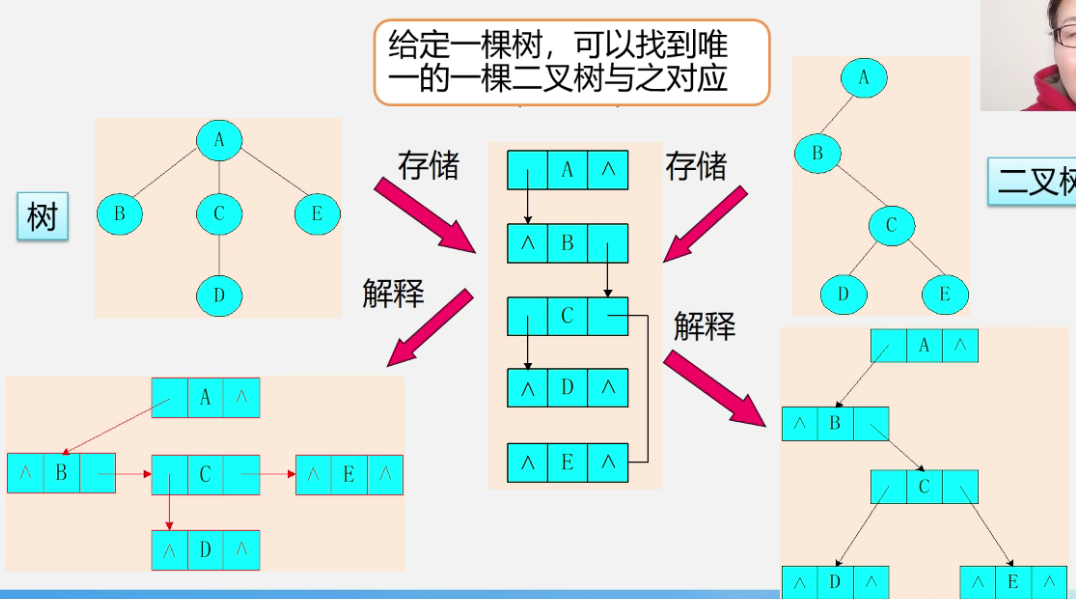
law
example

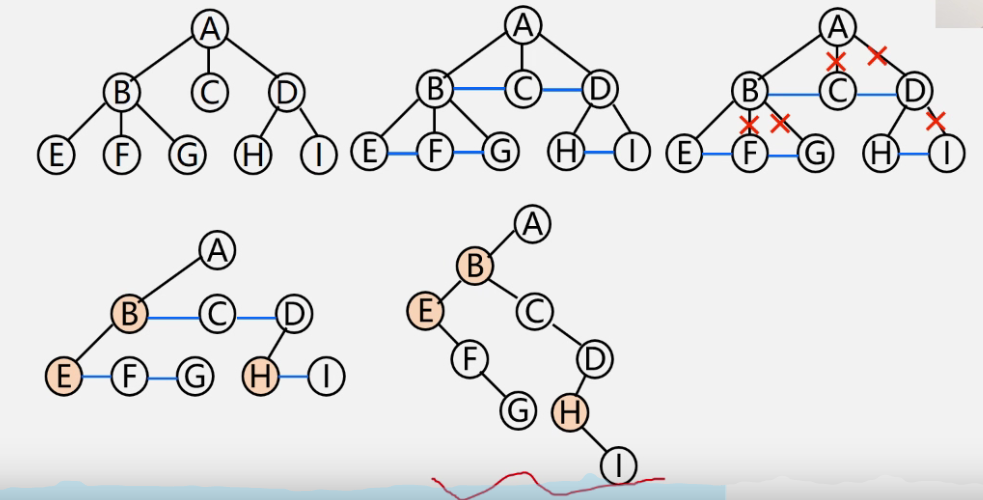
Binary tree to tree

example

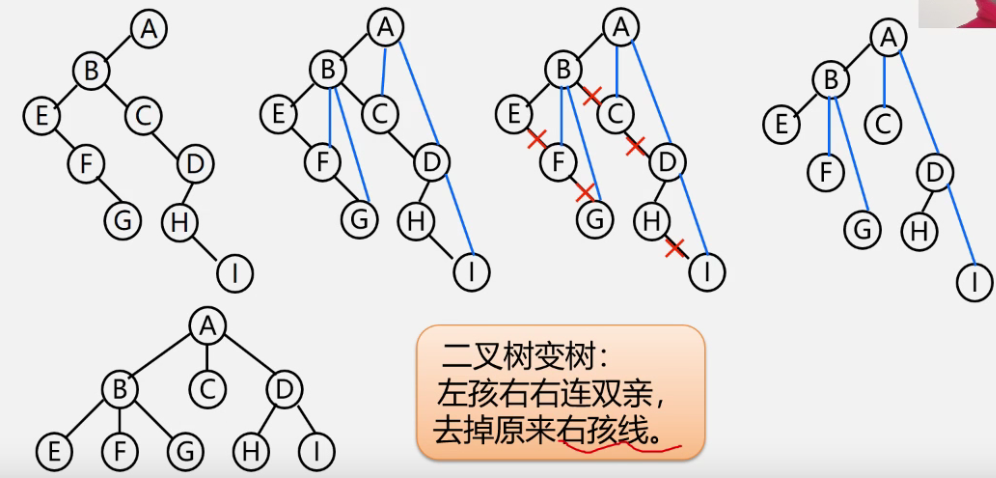
3. Transformation between forest and binary tree (relationship between binary tree and multiple trees)

Forest to binary tree

example

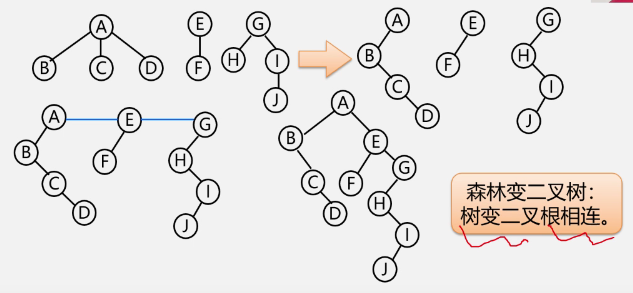
Binary tree into forest

example

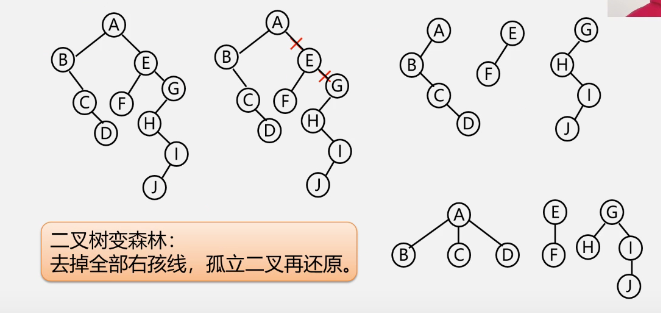
4. Traversal of trees and forests

Tree traversal (three ways)

Forest traversal

Preorder traversal
Medium order traversal
example

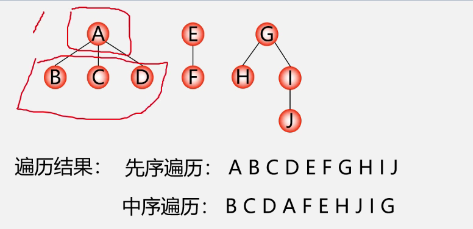
5, Huffman tree

1. Introduction

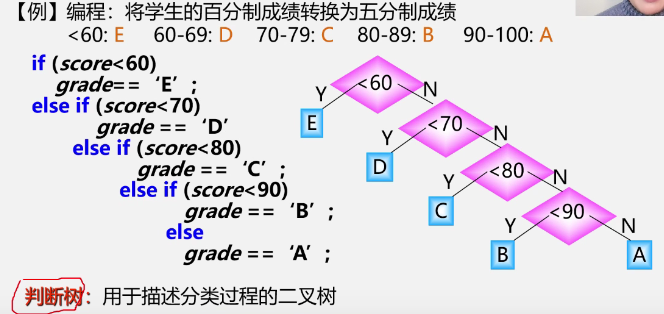
optimization
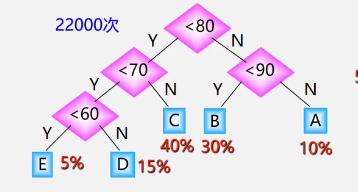
Huffman tree

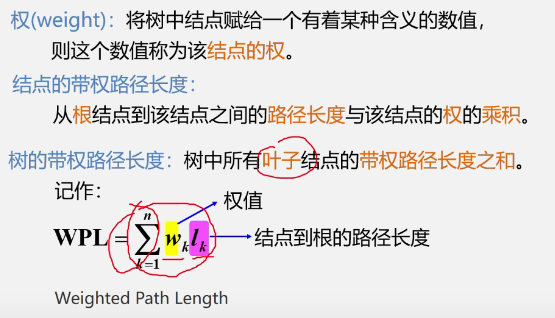
2. Basic concepts

Path, path length, weight

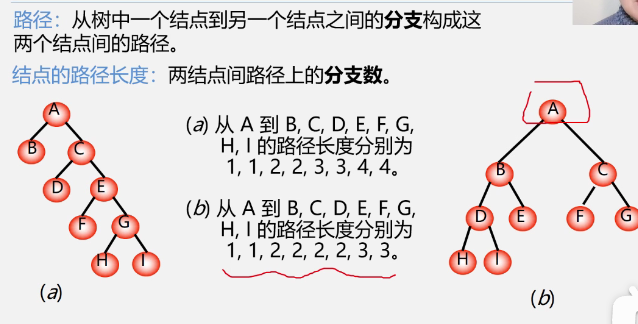
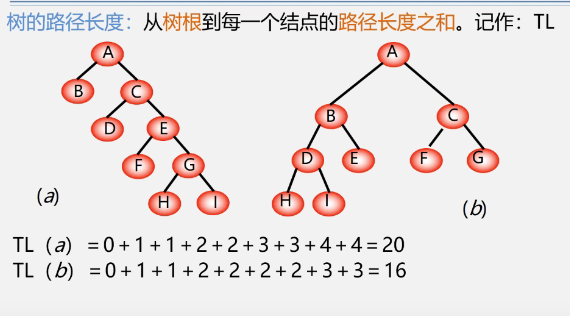
In the binary tree with the same number of nodes, the complete binary tree is the binary tree with the shortest path length

Huffman tree

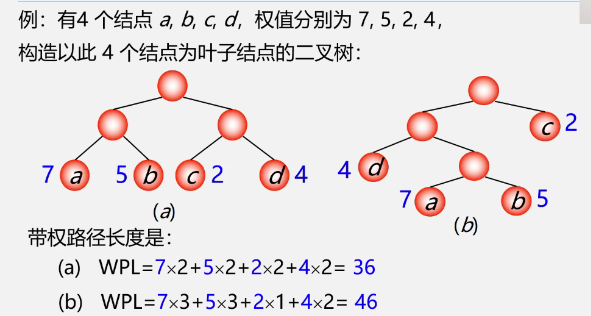
example

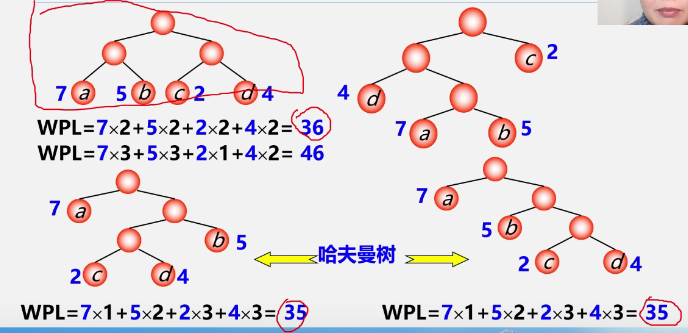
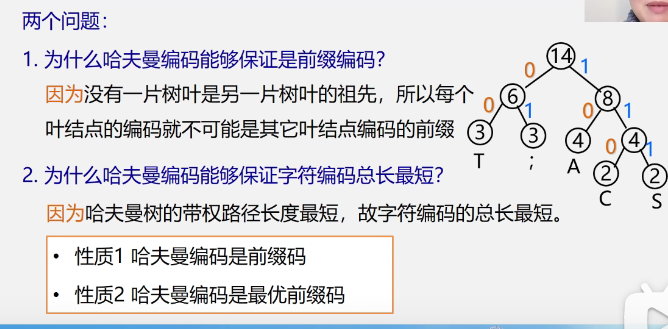
Characteristics of Huffman tree

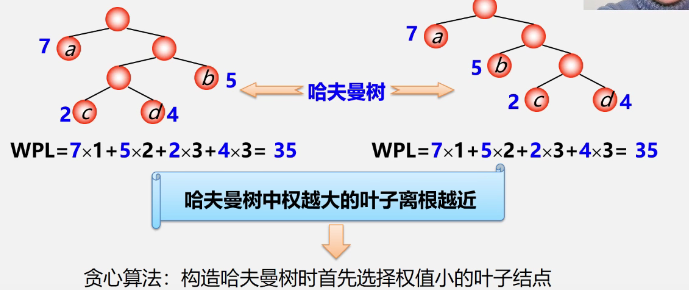
A full binary tree is not necessarily an optimal binary tree (Huffman tree)
The more powerful the leaf in the Huffman tree, the closer it is to the root
Huffman trees with the same weighted nodes are not unique

3. Construction algorithm of Huffman tree

C language implementation:

https://tyrantlucifer.com/44.html

Huffman algorithm (method of constructing Huffman tree)

example
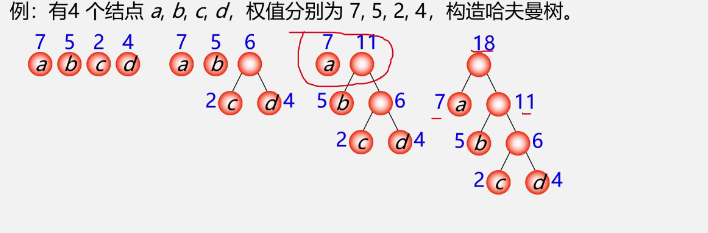
example

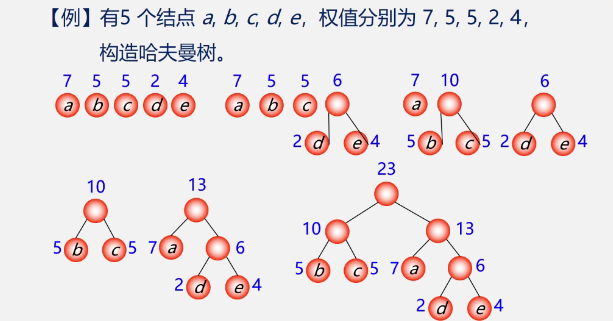
Characteristics of Huffman algorithm

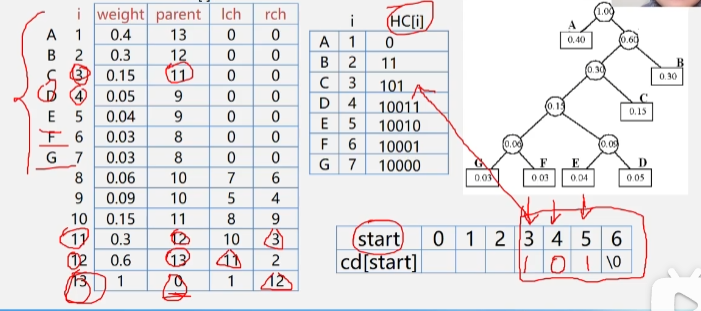
Implementation of Huffman tree construction algorithm

Sequential storage structure
example

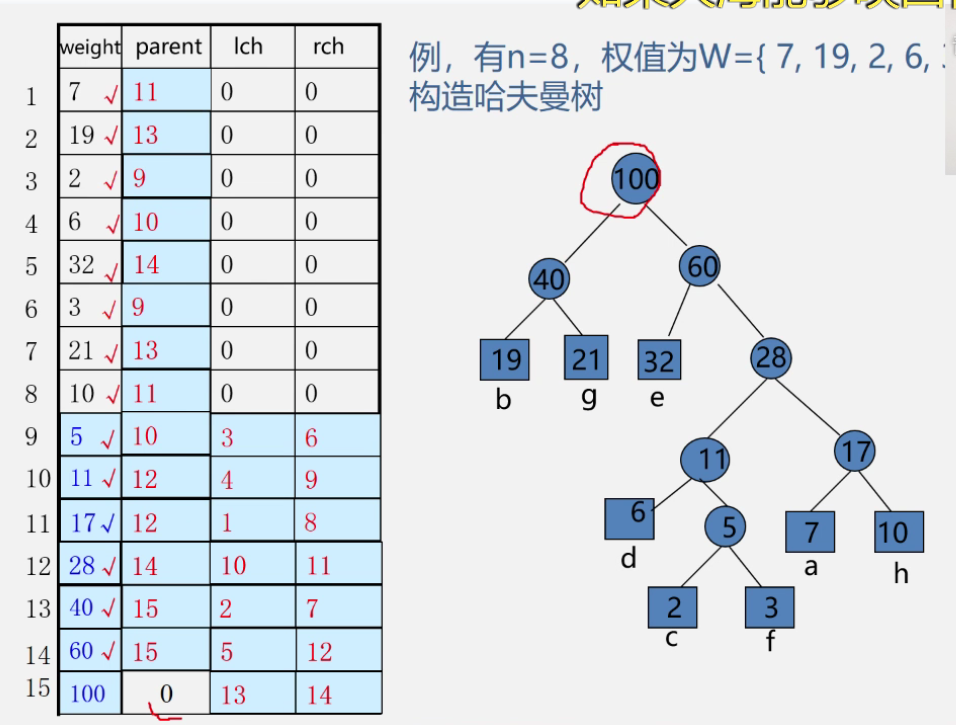
Algorithm implementation

code implementation

void CreatHuffmanTree(HuffmanTree HT,int n){//Constructing Huffman tree -- Huffman algorithm
	if(n<=1) return;
	m=2*n-1;	//The array has 2n-1 elements in total
	HT = new HTNode[m+1];	//Cell 0 is not used, HT[m] represents the root node
	for(i=1;i<=m;++i){	//Set lch, rch and parent of 2n-1 elements to 0
		HT[i].lch=0;
		HT[i].rch=0;
		HT[i].parent=0;
	}
	for(i=1;i<=n;++i)
		cin>>HT[i].weight;//Enter the weight value of the first n elements
    //After initialization, let's start building Huffman tree
    for(i=n+1;i<=m;i++){	//Merging to produce n-1 nodes -- Constructing Huffman tree
        Select(HT,i-1,s1,s2);	//In HT[k](1 ≤ K ≤ i-1), select two nodes whose parent domain is 0 and whose weight is the smallest, and return their sequence numbers s1 and s2 in HT
        HT[s1].parent=i;
        HT[s2].parent=i;	//Indicates that S1 and S2 are deleted from F
        HT[i].lch=s1;
        HT[i].rch=s2;	//S1 and S2 are the left and right children of i
        HT[i].weight=HT[s1].weight+HT[s2].weight;	//The weight of i is the sum of the weight of left and right children
        
    }
    
}

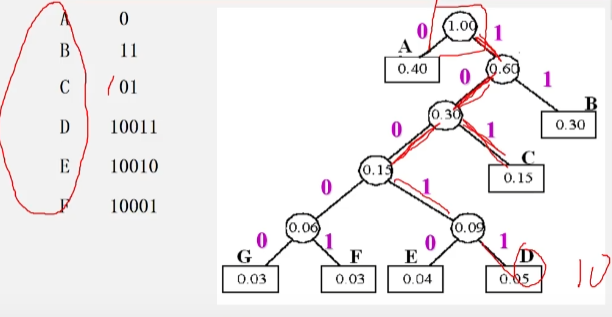
example
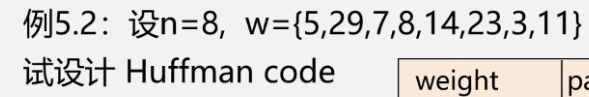
- initialization
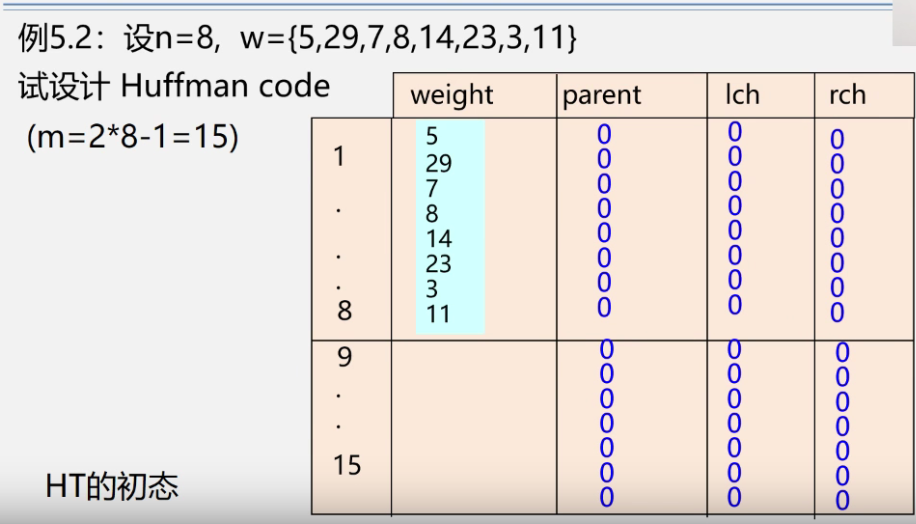
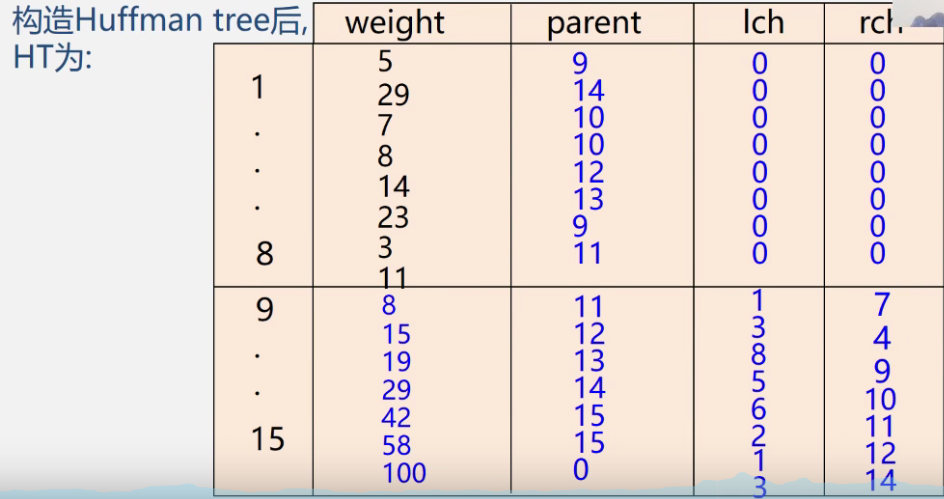
- Constructing Huffman tree

Application of Huffman tree -- Huffman coding

introduce

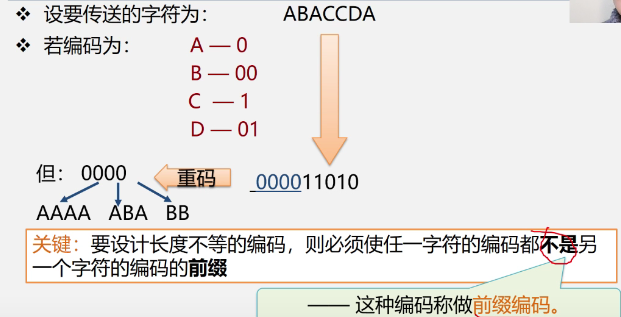
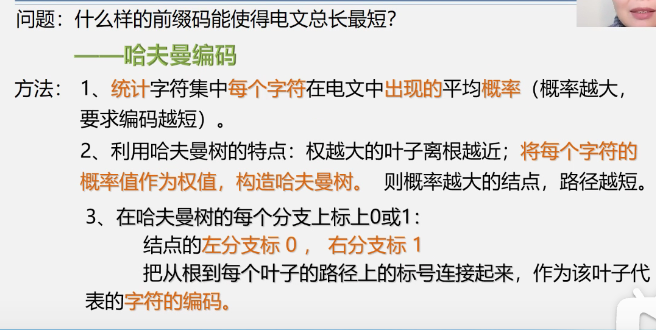
example

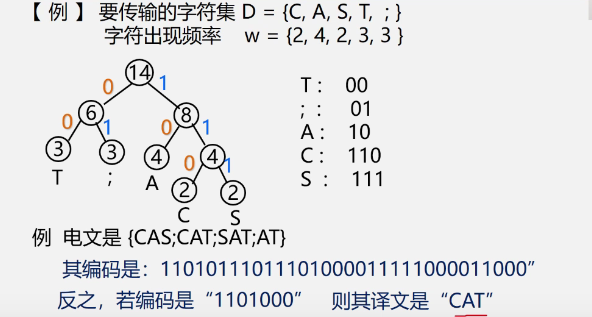
Properties of Huffman coding

Example 54

Implementation of Huffman coding algorithm

example
Algorithm description

4. Application of Huffman tree

Encoding and decoding of files

introduce

code

decode

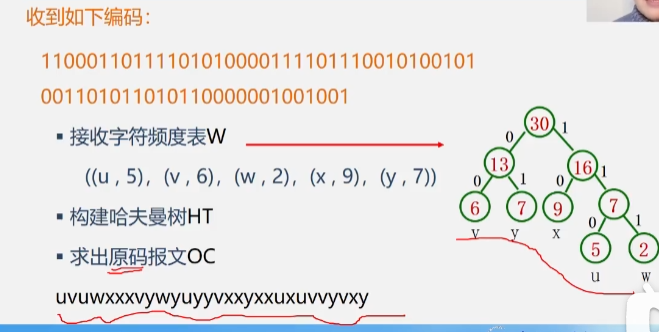
7, Partial code implementation

Solve the random code of vscode terminal: https://www.cnblogs.com/stu-jyj3621/p/12815080.html

The previous notes are pseudo code

Code implementation reference of this part:

Qingdao University MOOC: Data structure and algorithm practice

Great tutorial!

Supplementary review: C + + template, STL

#include <iostream>
#include <vector>
using namespace std;

//The vector vector is also a template

int main()
{
   vector<int> v;
   v.push_back(123);
   v.push_back(4);

   for (auto x : v) //For every element x in v
   {
       cout << x << endl;
   }
   cout << endl;
   // return 0;
}

Episode: mentality burst

Tap the code into the tutorial and find that auto is wrong

I searched the expected primary expression before '}' token for a long time, but I couldn't find it. Another search method: VSCODE auto reported an error, and finally found it 😭 https://bbs.csdn.net/topics/392167864?page=1

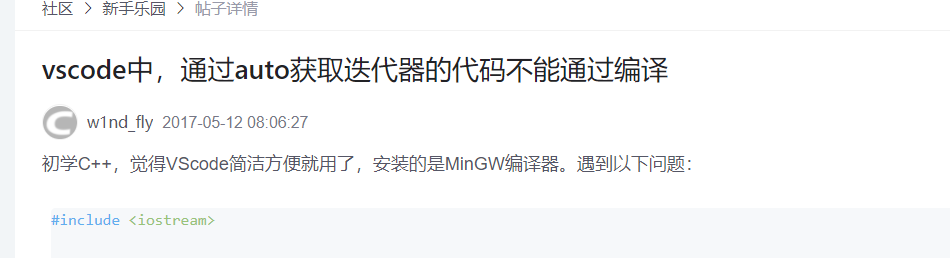And found one https://blog.csdn.net/weixin_42292229/article/details/113767569

But the link above doesn't solve my problem

In order to solve the auto error report, toss for a long time

First solve it in dev:

The first reference: https://blog.csdn.net/u011500062/article/details/44628441 , the following error will be reported
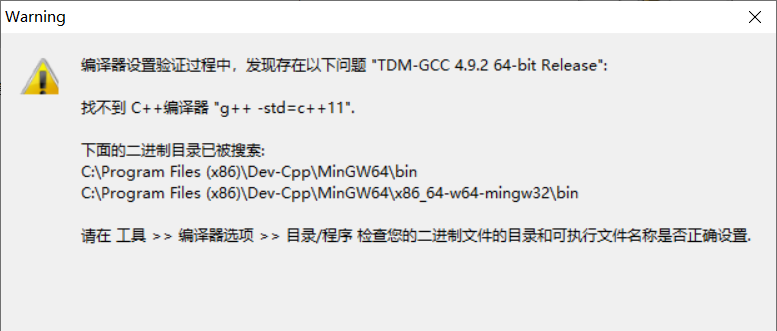
Finally solved this problem 😭

https://blog.csdn.net/Ljnoit/article/details/108153775

vscode... Gave up 😅😅😅… Checked for more than an hour

Searching the Internet for various methods is still useless

You can't change C++17 to 11 directly 😅

Use dev directly 😅

Press the object into the container

Create a class first

#include <iostream>
#include <vector>
using namespace std;

//The vector vector is also a template
class Stu{
private:
		string id;
		int score;
public:
	//Construction method
		Stu(string id,int score){
			this->id = id;
			this->score = score;
		} 
		friend ostream& operator << (ostream &o,const Stu& s);
		
}; 
ostream& operator << (ostream&o,const Stu& s){
	o <<"("<<s.id<<","<<s.score<<")";
	
} 
int main()
{
  Stu s("007",99);
  
  cout<<s<<endl;
}

Object push into container

#include <iostream>
#include <vector>
using namespace std;

//The vector vector is also a template
class Stu{
private:
		string id;
		int score;
public:
	//Construction method
		Stu(string id,int score){
			this->id = id;
			this->score = score;
		} 
		friend ostream& operator << (ostream &o,const Stu& s);
		
}; 
ostream& operator << (ostream&o,const Stu& s){
	o <<"("<<s.id<<","<<s.score<<")";
	
} 
int main()
{
//  Stu s("007",99);
//  
//  cout<<s<<endl;
	vector<Stu> v;
	//First Stu s("007",99); Then v.push_back(s); This is equivalent to copying, which is a little inefficient
	//It can be constructed in the container,
	v.emplace_back("S007",99);
	for(auto x:v)
	{
		cout<<x<<endl;
	 } 
	 return 0;
}

Chain implementation of tree and binary tree (C + +)

Construction tree

c + + structure template

#include <iostream>
using namespace std;
template <class Elem>
//typedef is C-style, and the template of C + + is used here
struct BinNode
{
    Elem data;
    BinNode<Elem> *left;
    BinNode<Elem> *right;
    //structure
    BinNode(Elem x)
    {
    	data = x;
		left = right = NULL; 
    }
};
//Write a binary tree with a class template 
template<class Elem> 
class BinTree{
protected:
	BinNode<Elem> *root;//Pointer to the root node
public:
	BinTree() {root = NULL;}//Construct empty tree
	BinTree(Elem r){
		root = new BinNode<Elem>(r);//Construct root node 
		
	}
	//Destructor
	~BinTree() {
	}
	
};
int main()
{
    BinTree<int> bt(11); 
    return 0;
}

Traversal tree

Preorder traversal

#include <iostream>
using namespace std;
template <class Elem>
//typedef is C-style, and the template of C + + is used here
struct BinNode
{
    Elem data;
    BinNode<Elem> *left;
    BinNode<Elem> *right;
    //structure
    BinNode(Elem x)
    {
    	data = x;
		left = right = NULL; 
    }
};
//Write a binary tree with a class template 
template<class Elem> 
class BinTree{
protected:
	BinNode<Elem> *root;//Pointer to the root node
	 
	void rpreprint(BinNode<Elem> *r)//Recursive print preorder traversal 
	{
		if(r==NULL)	return ;//Null pointer call returns immediately
		cout<< r->data <<" ";
		rpreprint(r->left);
		rpreprint(r->right);
	 } 
public:
	BinTree() {root = NULL;}//Construct empty tree
	BinTree(Elem r){
		root = new BinNode<Elem>(r);//Construct root node 
		
	}
	//Preorder traversal
	void preprint(){
		rpreprint(root); 
		cout << endl; 
	} 
	//Destructor
	~BinTree() {
	}
	
};
int main()
{
    BinTree<int> bt(11); 
    bt.preprint(); 
    return 0;
}

//structure
BinNode(Elem x)
{
	data = x;
	left = right = NULL; 
}

};
//Write a binary tree with a class template
template
class BinTree{
protected:
BinNode *root;// Pointer to the root node
public:
BinTree() {root = NULL;} / / construct an empty tree
BinTree(Elem r){
root = new BinNode ®;// Construct root node

}
//Destructor
~BinTree() {
}

};
int main()
{
BinTree bt(11);
return 0;
}

#### Traversal tree

- Preorder traversal

~~~c
#include <iostream>
using namespace std;
template <class Elem>
//typedef is C-style, and the template of C + + is used here
struct BinNode
{
    Elem data;
    BinNode<Elem> *left;
    BinNode<Elem> *right;
    //structure
    BinNode(Elem x)
    {
    	data = x;
		left = right = NULL; 
    }
};
//Write a binary tree with a class template 
template<class Elem> 
class BinTree{
protected:
	BinNode<Elem> *root;//Pointer to the root node
	 
	void rpreprint(BinNode<Elem> *r)//Recursive print preorder traversal 
	{
		if(r==NULL)	return ;//Null pointer call returns immediately
		cout<< r->data <<" ";
		rpreprint(r->left);
		rpreprint(r->right);
	 } 
public:
	BinTree() {root = NULL;}//Construct empty tree
	BinTree(Elem r){
		root = new BinNode<Elem>(r);//Construct root node 
		
	}
	//Preorder traversal
	void preprint(){
		rpreprint(root); 
		cout << endl; 
	} 
	//Destructor
	~BinTree() {
	}
	
};
int main()
{
    BinTree<int> bt(11); 
    bt.preprint(); 
    return 0;
}

Keywords: C C++ data structure tree STL

Added by caedo on Thu, 25 Nov 2021 00:59:12 +0200

Programming VIP

Data structure and algorithm learning note tree

Data structure and algorithm learning notes (7) tree

1, Definition of tree and binary tree

1. Trees

Definition of tree

Basic terms of trees

Comparison between tree structure and linear structure

2. Binary tree

Definition of binary tree

The difference between binary tree and tree

Basic form of binary tree

3. Abstract data type definition of tree and binary tree

2, Properties and storage structure of binary tree

1. Properties of binary tree

① Binary tree properties 1, 2, 3

② Two special forms of binary trees: full binary tree and complete binary tree

Definition and characteristics

Relationship between the two

③ Properties 4 and 5 of binary tree (two properties of complete binary tree)

2. Storage structure of binary tree

① Sequential storage

② Chain storage

Binary linked list

Trigeminal linked list

3, Traversing binary tree and clue binary tree

1. Overview of traversal method

Operation definition of preordered traversal of binary tree

Operation definition of traversing binary tree in middle order

Operation definition of post order traversal of binary tree

example

2. Determine the binary tree according to the traversal sequence

3. Implementation of traversal method of binary tree

Preorder traversal recursive algorithm

Middle order traversal recursive algorithm

Postorder traversal recursive algorithm

Comparative analysis of three recursive traversal algorithms

Middle order traversal non recursive algorithm

Hierarchical traversal algorithm of binary tree

4. Application of binary tree traversal algorithm

Algorithm for establishing binary tree

The binary linked list of binary tree is established by traversing the sequence in advance

Duplicate binary tree

Calculate the depth of the binary tree

Calculate the total number of binary tree nodes

Calculate the number of leaf nodes of binary tree

5. Clue binary tree

Storage of clue binary tree

Preordered clue binary tree

Middle order clue binary tree

Post ordered clue binary tree

Add head node

4, Trees and forests

1. Storage structure of tree

Parental representation

Child list

Child brother representation (binary tree representation, binary linked list representation)

2. Transformation between tree and binary tree

Tree to binary tree

Binary tree to tree

3. Transformation between forest and binary tree (relationship between binary tree and multiple trees)

Forest to binary tree

Binary tree into forest

4. Traversal of trees and forests

Tree traversal (three ways)

Forest traversal

5, Huffman tree

1. Introduction

2. Basic concepts

Path, path length, weight

Huffman tree

Characteristics of Huffman tree

3. Construction algorithm of Huffman tree

Huffman algorithm (method of constructing Huffman tree)

Characteristics of Huffman algorithm

Implementation of Huffman tree construction algorithm

Application of Huffman tree -- Huffman coding

Properties of Huffman coding

Implementation of Huffman coding algorithm

4. Application of Huffman tree