Tip: after the article is written, the directory can be generated automatically. Please refer to the help document on the right for how to generate it

summary

I have seen such a saying before that language is only a tool, and algorithm is the soul of programming. Indeed, the status of algorithms in computer science is really important. In the written interview of many large companies, the investigation of algorithm mastery occupies a large part. Whether for the interview or the improvement of their programming ability, it is necessary to take time to study common algorithms. ***

Algorithm Introduction
Algorithm refers to the accurate and complete description of the problem-solving scheme. It is a series of clear instructions to solve the problem. The algorithm represents the strategy mechanism to solve the problem in a systematic way. There may be different algorithms for solving the same problem. In order to measure the advantages and disadvantages of an algorithm, two concepts of spatial complexity and time complexity are proposed.

• Time complexity

In general, the number of times the basic operation in the algorithm is repeated is a function f(n) of the problem scale n, and the time measurement of the algorithm is recorded as * * T(n) = O(f(n)) * *, which means that with the increase of the problem scale n, the growth rate of the algorithm execution time is the same as that of f(n), which is called the asymptotic time complexity of the algorithm, or time complexity for short. Here we need to focus on understanding this growth rate.

• Spatial complexity

Space complexity is a measure of the amount of storage space temporarily occupied by an algorithm during operation, which is recorded as S(n)=O(f(n)). The advantages and disadvantages of an algorithm are mainly measured from two aspects: the execution time and the storage space occupied by the algorithm.

1, Search algorithm

Search and sorting are the most basic and important two kinds of algorithms. It is very important to master these two kinds of algorithms and analyze the performance of these algorithms. These two kinds of algorithms mainly include binary search, quick sort, merge sort and so on.

Search of sequential storage structure

Sequential search is also called linear search. Its process is: compare with the given keyword one by one from the first or last element of the lookup table. If the keyword of a record is equal to the given value, the lookup is successful. Otherwise, If the keyword and given value of the first (last) record are not equal, it indicates that there is no record in the table and the search is unsuccessful. Its disadvantage is low efficiency.

/**
 * Sequential search
 * 
 * @param a
 *            array
 * @param key
 *            Keywords to be found
 * @return Keyword subscript
 */
public static int sequentialSearch(int[] a, int key) {
	for (int i = 0; i < a.length; i++) {
		if (a[i] == key)
			return i;
	}
	return -1;
}

This code is very simple, which is to check whether there is a keyword key in array A. when you need to find records with complex table structure, you only need to define array A and keyword key as the table structure and data type you need.

Sequential table lookup optimization

/**
 * Sequential search
 * 
 * @param a
 *            array
 * @param key
 *            Keywords to be found
 * @return Keyword subscript
 */
public static int sequentialSearch(int[] a, int key) {
	for (int i = 0; i < a.length; i++) {
		if (a[i] == key)
			return i;
	}
	return -1;
}

This kind of "sentry" placed at the end of the search direction eliminates the small skill of judging whether the search position crosses the boundary after each comparison in the search process. It seems to be little different from the original, but when the total data is large, the efficiency is greatly improved. It is a very good coding skill. Of course, "sentry" does not have to start in the array, but also at the end.

Search of chain storage structure

Linked list traversal

Half search (binary search)

Binary search technology, also known as binary search. Its premise is that the records in the linear table must be in order of key codes (usually from small to large), and the linear table must be stored in order. The basic idea of half search is: in the ordered table, take the intermediate record as the comparison object. If the given value is equal to the keyword of the intermediate record, the search is successful; If the given value is less than the keyword of the intermediate record, continue to search in the left half of the intermediate record; If the given value is greater than the keyword of the intermediate record, continue to search in the right half of the intermediate record. Repeat the above process until the search is successful or there is no record in all search areas and the search fails.

/**
 * Half search
 * 
 * @param a
 *            array
 * @param key
 *            Keywords to be found
 * @return Returns a half subscript, - 1 indicates that the keyword does not exist
 */
public static int binarySearch(int[] a, int key) {
	int low, mid, high;
	low = 0;// Minimum subscript
	high = a.length - 1;// Maximum subscript
	while (low <= high) {
		mid = (high + low) / 2;// Half subscript
		if (key > a[mid]) {
			low = mid + 1; // If the keyword is greater than the half value, the minimum subscript is adjusted to the next digit of the half subscript
		} else if (key < a[mid]) {
			high = mid - 1;// If the keyword is smaller than the half value, the maximum subscript is adjusted to the previous digit of the half subscript
		} else {
			return mid; // When key == a[mid], the half subscript is returned
		}
	}
	return -1;

The algorithm is easy to understand, and we can also feel its efficiency is very high. But how high is it? The key is the time complexity analysis of this algorithm.

First, we draw the search process of the array into a binary tree. If the search keyword is not an intermediate record, half search is equivalent to dividing the static ordered search table into two subtrees, that is, the search result only needs to find half of the data records, which is equal to half the workload, and then continue to half search. Of course, the efficiency is very high.

According to the property 4 of binary tree, the depth of complete binary tree with n nodes is [log2n]+1. Here, although it is determined that the binary tree is not a complete binary tree by half search, it can be concluded from the same derivation that the worst case is to find the keyword or the number of search failures is [log2n]+1, and the best case is 1.
Therefore, the time complexity of our halved algorithm is O(logn), which is obviously much better than the O(n) time complexity of sequential search.
However, since the precondition of folding primary lookup is that ordered tables need to be stored in order, for static lookup tables, they will not change after one sorting. Such an algorithm has been better. However, for data sets that require frequent insert or delete operations, maintaining orderly sorting will bring a lot of workload, so it is not recommended.

Other search algorithms

java implementation of common search algorithms

2, Sorting algorithm

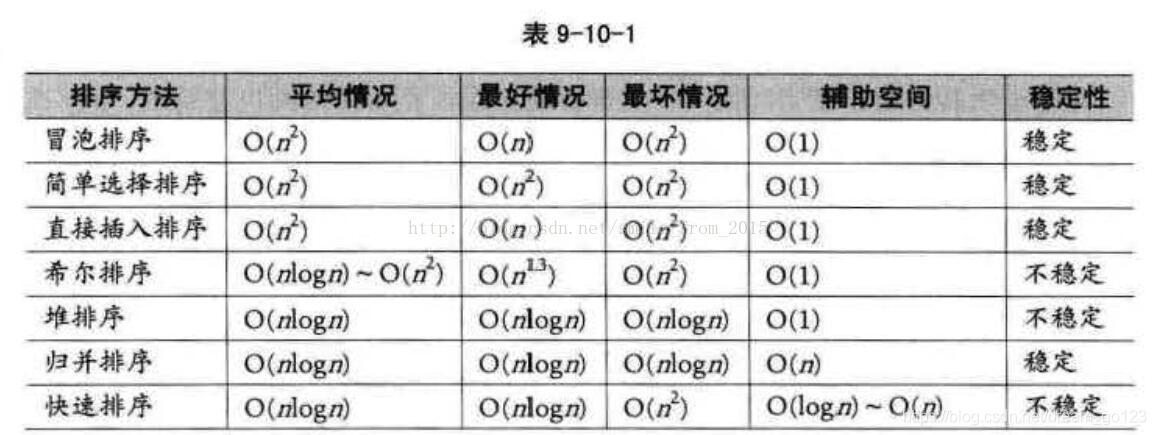
Sorting spatiotemporal complex stability summary

Simple selection sort

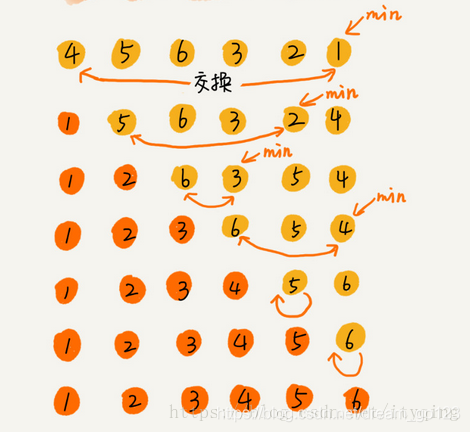
The basic idea of selective sorting is to select the record with the smallest keyword in n-i+1(i=1,2,..., n-1) records as the ith record of the ordered sequence. We first introduce the simple selection sorting method.
Simple selection sort is to select the record with the smallest keyword from n-i + 1 records through the comparison between n - i keywords, and exchange it with the I (1 < = I < = n) record.
Select sort to divide the array into sorted and unordered intervals. The initial sorted interval is empty. Each time, the smallest element selected from the unordered interval is inserted at the end of the sorted interval until the unordered interval is empty.

public class SelectionSort {

	public static void selectionSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		for (int i = 0; i < arr.length - 1; i++) {
			int minIndex = i;
			for (int j = i + 1; j < arr.length; j++) {
				minIndex = arr[j] < arr[minIndex] ? j : minIndex;
			}
			swap(arr, i, minIndex);
		}
	}

	public static void swap(int[] arr, int i, int j) {
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}
}

Bubble sorting

Bubble sorting only operates on two adjacent data. Each bubbling operation will compare two adjacent elements to see whether they meet the size relationship requirements. If not, let them be interchanged.

public class BubbleSort {

	public static void bubbleSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		for (int e = arr.length - 1; e > 0; e--) {
			for (int i = 0; i < e; i++) {
				if (arr[i] > arr[i + 1]) {
					swap(arr, i, i + 1);
				}
			}
		}
	}

	public static void swap(int[] arr, int i, int j) {
		arr[i] = arr[i] ^ arr[j];
		arr[j] = arr[i] ^ arr[j];
		arr[i] = arr[i] ^ arr[j];
	}
}

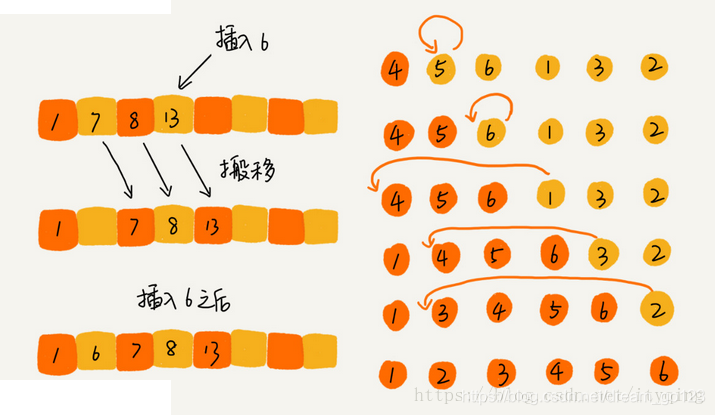
Insert sort

Insert sort divides the array data into sorted intervals and unordered intervals. The initial sorted interval has only one element, the first element of the array. Take out an element from the unordered interval and insert it into the appropriate position of the sorted interval until the unordered interval is empty.

public class InsertionSort {

	public static void insertionSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		for (int i = 1; i < arr.length; i++) {
			for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
				swap(arr, j, j + 1);
			}
		}
	}

	public static void swap(int[] arr, int i, int j) {
		arr[i] = arr[i] ^ arr[j];
		arr[j] = arr[i] ^ arr[j];
		arr[i] = arr[i] ^ arr[j];
	}
}

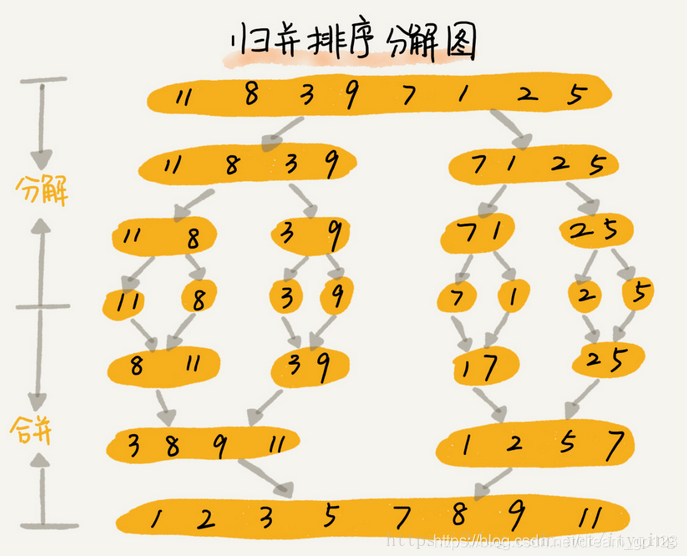
Merge sort

If you want to sort an array, we first divide the array into two parts from the middle, then sort the two parts respectively, and then merge the two parts in order, so that the whole array is in order.

public class MergeSort {

	public static void mergeSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		mergeSort(arr, 0, arr.length - 1);
	}

	public static void mergeSort(int[] arr, int l, int r) {
		if (l == r) {
			return;
		}
		int mid = l + ((r - l) >> 1);
		mergeSort(arr, l, mid);
		mergeSort(arr, mid + 1, r);
		merge(arr, l, mid, r);
	}

	public static void merge(int[] arr, int l, int m, int r) {
		int[] help = new int[r - l + 1];
		int i = 0;
		int p1 = l;
		int p2 = m + 1;
		while (p1 <= m && p2 <= r) {
			help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
		}
		while (p1 <= m) {
			help[i++] = arr[p1++];
		}
		while (p2 <= r) {
			help[i++] = arr[p2++];
		}
		for (i = 0; i < help.length; i++) {
			arr[l + i] = help[i];
		}
	}
}

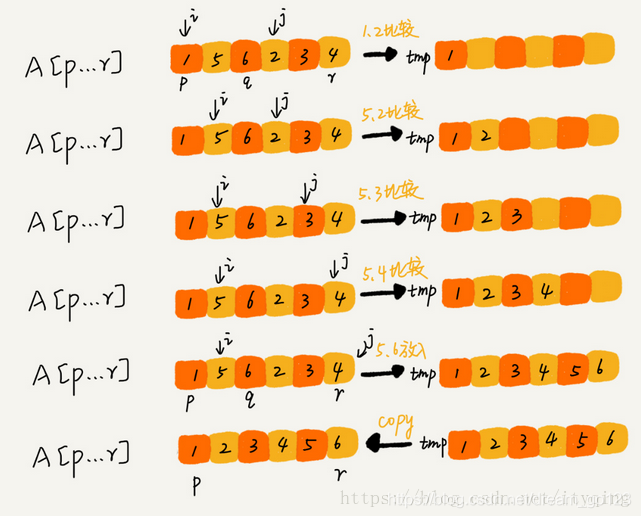
Heap sort

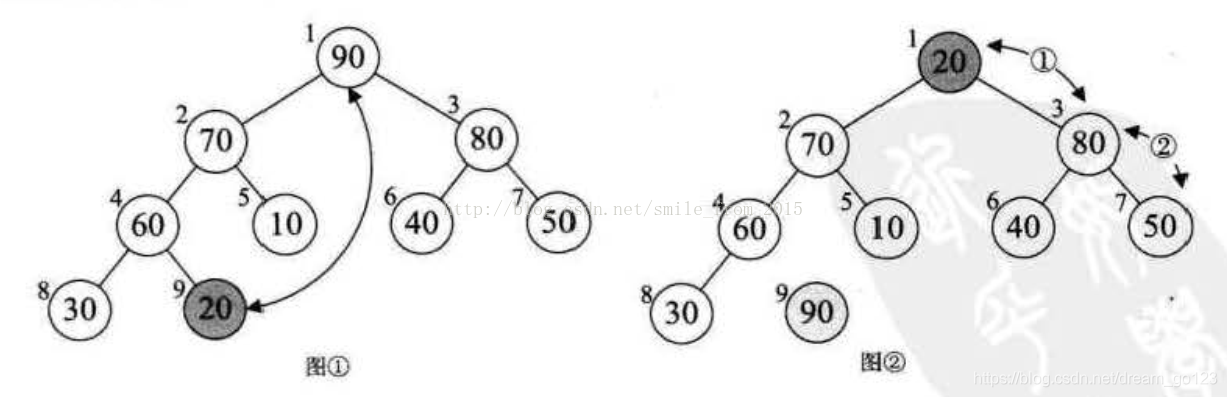
Heap sort is a sort method using heap (assuming large top heap). Its basic idea is to construct the sequence to be sorted into a large top heap. At this time, the maximum value of the whole sequence is the root node at the top of the heap. Move it away (in fact, it is exchanged with the end element of the heap array, which is the maximum value). Then reconstruct the remaining n - 1 sequences into a heap, so as to find the sub - small value in the n elements. If you execute it repeatedly, you can get an ordered sequence.

For example, as shown in figure 9-7-4, figure ① is a large top heap, 90 is the maximum value, and 90 is interchanged with 20 (tail element), as shown in figure ②. At this time, 90 becomes the last element of the whole heap sequence, and 20 is adjusted so that nodes other than 90 continue to meet the definition of large top heap (all nodes are greater than or equal to their children), as shown in figure ③, Then consider swapping 30 with 80

public class HeapSort {

	public static void heapSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		for (int i = 0; i < arr.length; i++) { // Convert to large root pile
			heapInsert(arr, i);
		}
		int size = arr.length;
		swap(arr, 0, --size);
		while (size > 0) {
			heapify(arr, 0, size);
			swap(arr, 0, --size);
		}
	}

	public static void heapInsert(int[] arr, int index) {
		while (arr[index] > arr[(index - 1) / 2]) { // Compare size with parent node
			swap(arr, index, (index - 1) /2);
			index = (index - 1)/2 ;
		}
	}

	public static void heapify(int[] arr, int index, int size) {
		int left = index * 2 + 1;
		while (left < size) {
			int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
			largest = arr[largest] > arr[index] ? largest : index;
			if (largest == index) {
				break;
			}
			swap(arr, largest, index);
			index = largest;
			left = index * 2 + 1;
		}
	}

	public static void swap(int[] arr, int i, int j) {
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}
}

Quick sort

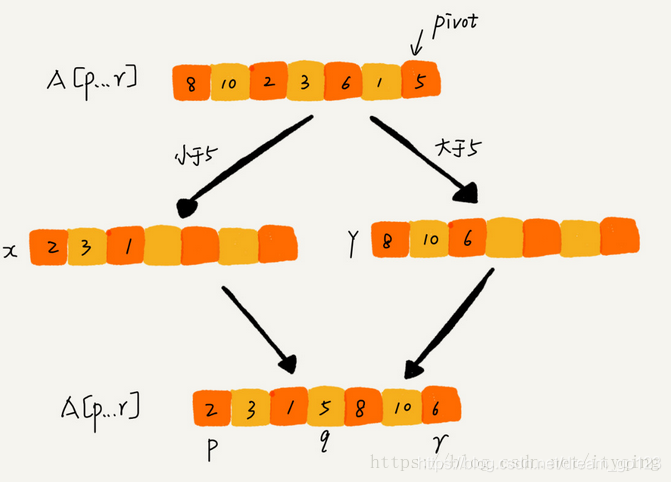
Idea of fast sorting: if we want to sort a group of data with subscripts from P to R in the array, we choose any data from P to r as the pivot (partition point)- We traverse the data between P and R, put those less than pivot on the left, those greater than pivot on the right, and pivot in the middle. After this step, the data from array p to R is divided into three parts. The front p to q-1 is less than pivot, the middle is pivot, and the rear q+1 to R is greater than pivot.

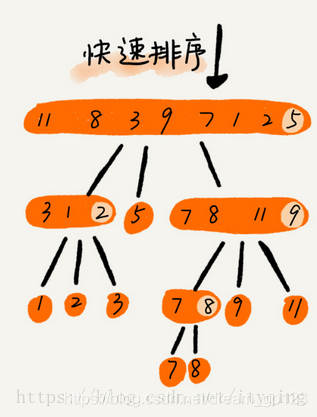
The idea of divide and rule

public class QuickSort {

	public static void quickSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		quickSort(arr, 0, arr.length - 1);
	}

	public static void quickSort(int[] arr, int l, int r) {
		if (l < r) {
			swap(arr, l + (int) (Math.random() * (r - l + 1)), r);  // Random last reference value
			int[] p = partition(arr, l, r);
			quickSort(arr, l, p[0] - 1);
			quickSort(arr, p[1] + 1, r);
		}
	}

	public static int[] partition(int[] arr, int l, int r) {
		int less = l - 1;
		int more = r;
		while (l < more) {
			if (arr[l] < arr[r]) {
				swap(arr, ++less, l++);
			} else if (arr[l] > arr[r]) {
				swap(arr, --more, l);
			} else {
				l++;
			}
		}
		swap(arr, more, r);
		return new int[] { less + 1, more };
	}

	public static void swap(int[] arr, int i, int j) {
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}
}

Sort comparator

package class03;

import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.TreeSet;

public class Code03_Comparator {

	public static class Student {
		public String name;
		public int id;
		public int age;

		public Student(String name, int id, int age) {
			this.name = name;
			this.id = id;
			this.age = age;
		}
	}

	public static class IdAscendingComparator implements Comparator<Student> {

		@Override
		public int compare(Student o1, Student o2) {
			return o1.id - o2.id;
		}

	}

	public static class IdDescendingComparator implements Comparator<Student> {

		@Override
		public int compare(Student o1, Student o2) {
			return o2.id - o1.id;
		}

	}

	public static class AgeAscendingComparator implements Comparator<Student> {

		@Override
		public int compare(Student o1, Student o2) {
			return o1.age - o2.age;
		}

	}

	public static class AgeDescendingComparator implements Comparator<Student> {

		@Override
		public int compare(Student o1, Student o2) {
			return o2.age - o1.age;
		}

	}

	public static void printStudents(Student[] students) {
		for (Student student : students) {
			System.out.println("Name : " + student.name + ", Id : " + student.id + ", Age : " + student.age);
		}
	}

	public static void printArray(Integer[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	public static class MyComp implements Comparator<Integer> {

		@Override
		public int compare(Integer o1, Integer o2) {
			return o2 - o1;
		}

	}

	public static void main(String[] args) {
		Student student1 = new Student("A", 2, 23);
		Student student2 = new Student("B", 3, 21);
		Student student3 = new Student("C", 1, 22);

		Student[] students = new Student[] { student1, student2, student3 };

		Arrays.sort(students, new IdAscendingComparator());
		printStudents(students);
		System.out.println("===========================");

		Arrays.sort(students, new IdDescendingComparator());
		printStudents(students);
		System.out.println("===========================");

		Arrays.sort(students, new AgeAscendingComparator());
		printStudents(students);
		System.out.println("===========================");

		Arrays.sort(students, new AgeDescendingComparator());
		printStudents(students);
		System.out.println("===========================");
		System.out.println("===========================");
		System.out.println("===========================");
		System.out.println("===========================");

		PriorityQueue<Student> maxHeapBasedAge = new PriorityQueue<>(new AgeDescendingComparator());
		maxHeapBasedAge.add(student1);
		maxHeapBasedAge.add(student2);
		maxHeapBasedAge.add(student3);
		while (!maxHeapBasedAge.isEmpty()) {
			Student student = maxHeapBasedAge.poll();
			System.out.println("Name : " + student.name + ", Id : " + student.id + ", Age : " + student.age);
		}
		System.out.println("===========================");

		PriorityQueue<Student> minHeapBasedId = new PriorityQueue<>(new IdAscendingComparator());
		minHeapBasedId.add(student1);
		minHeapBasedId.add(student2);
		minHeapBasedId.add(student3);
		while (!minHeapBasedId.isEmpty()) {
			Student student = minHeapBasedId.poll();
			System.out.println("Name : " + student.name + ", Id : " + student.id + ", Age : " + student.age);
		}
		System.out.println("===========================");
		System.out.println("===========================");
		System.out.println("===========================");

		TreeSet<Student> treeAgeDescending = new TreeSet<>(new AgeDescendingComparator());
		treeAgeDescending.add(student1);
		treeAgeDescending.add(student2);
		treeAgeDescending.add(student3);

		Student studentFirst = treeAgeDescending.first();
		System.out.println("Name : " + studentFirst.name + ", Id : " + studentFirst.id + ", Age : " + studentFirst.age);

		Student studentLast = treeAgeDescending.last();
		System.out.println("Name : " + studentLast.name + ", Id : " + studentLast.id + ", Age : " + studentLast.age);
		System.out.println("===========================");

	}

}

reference resources:
Summary of common data structures and algorithms (Part 2)
java implementation of common search algorithms