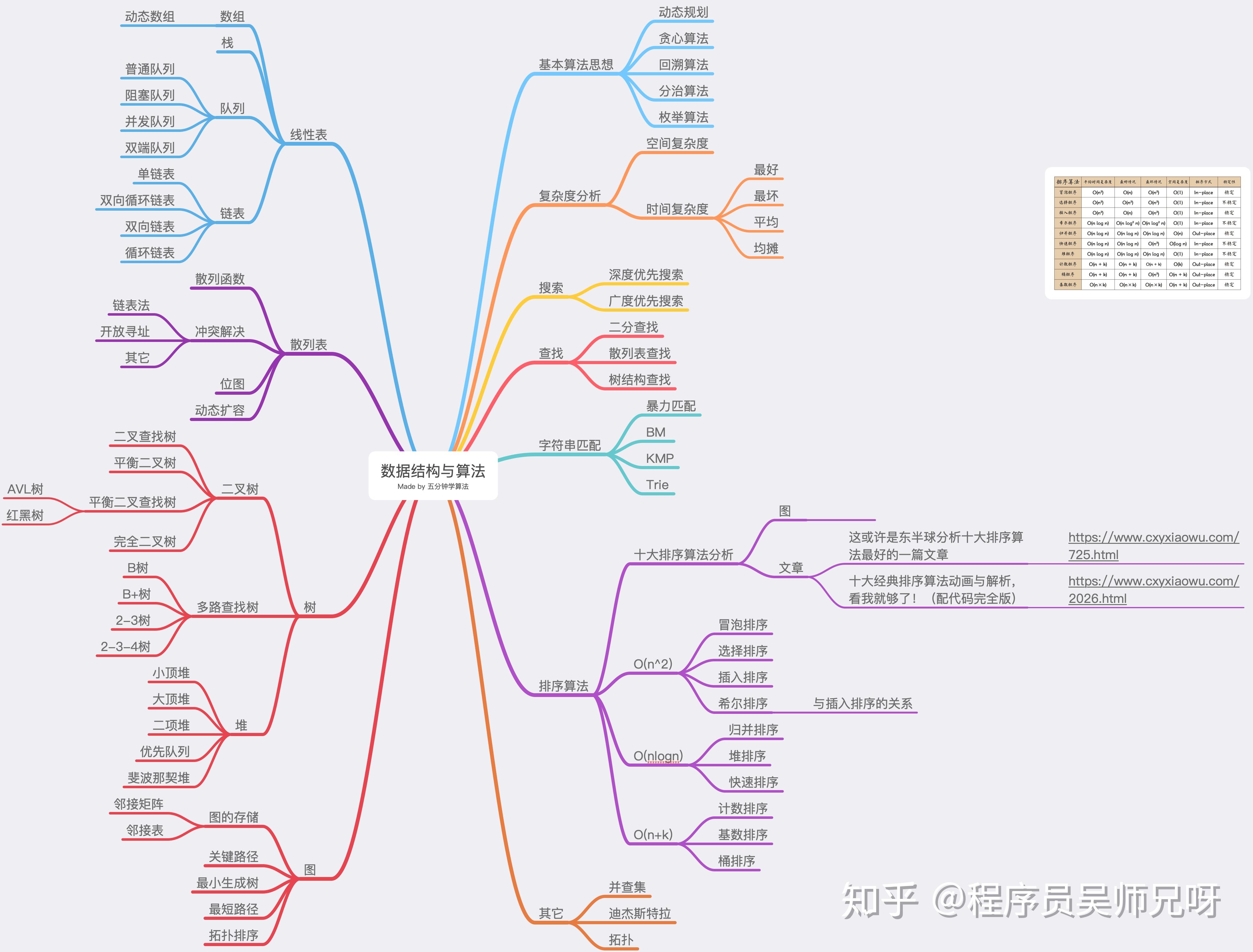
Data structure and algorithm architecture.
1, Time complexity and space complexity
1. What are time complexity and space complexity
How to distinguish the quality of an algorithm, if executed in the program, will be disturbed by various factors, so the concepts of time complexity and space complexity are introduced.
The complexity of this algorithm is that it takes a lot of time to execute.
The asymptotic time complexity of the algorithm: t (n) = O (f (n)) ---- > large o representation.
2. Time complexity
For example, our algorithm needs to be executed many times, so what is its expression? Take the highest order item.
- For example, the most basic line of code is O (1);
- If the calculation time in an algorithm is the same, it must be that the more times it takes, the longer it takes, and it increases linearly. For example, if it takes 1 minute to eat chicken legs every time, it executes n times, and the time is n minutes, so its time complexity is O (n);
- If you calculate the sum of 1 to 100, the calculated expression is (1 + n) * n/2 – > that is, 0.5n ² + 0.5n, ignoring the power of N, then its time complexity is O (n ²)
- For another example, if a rope is 16cm long and the remaining half is cut off each time, then how long will there be 1cm left? Then logarithms need to be used. At this time, the time complexity is O (log16)
3. Spatial complexity
Space complexity does not need to be understood too deeply, but it is important to know that it does not describe how much memory is used, but rather compare the memory changes.
- For example, a variable = 1, and then + + assignment is performed on it every time. The variable is still one, but the memory occupation will not change with constant assignment, so it is still 1
- Another example is a for loop. Each time a new variable is created, its space complexity must be n
- If it is a two-dimensional array and assigned with a double-layer for loop, its space complexity is n ²
2, Array
1. Introduction
Array is one of the most basic data structures. It can store a limited number of elements (fixed length) and can be added, deleted, modified and queried
2. Code implementation
public class MyArray {
//Define an array
int[] elements;
//Initialize array
public MyArray(){
elements = new int[0];
}
//Gets the length of the array
public int size(){
return elements.length;
}
//Add an element to the end of the array
public void add(int ele){
int[] newArr = new int[elements.length + 1];
for (int i = 0;i < elements.length;i++){
newArr[i] = elements[i];
}
newArr[elements.length] = ele;
elements = newArr;
}
//Method of traversing array
public void arrayShow(){
System.out.println(Arrays.toString(elements));
}
//Delete an element
public void delete(int index){
if (index < 0 || index > elements.length - 1){
throw new RuntimeException("Incorrect incoming subscript");
}
int[] newArr = new int[elements.length - 1];
for (int i = 0;i < newArr.length;i++){
if (i < index){
newArr[i] = elements[i];
}else{
newArr[i] = elements[i + 1];
}
}
elements = newArr;
}
//Extract the element at the specified location
public int get(int index){
if (index < 0 || index > elements.length -1){
throw new RuntimeException("The incoming subscript is incorrect and the element cannot be read");
}
return elements[index];
}
//Inserts an element into the specified location
public void insert(int index,int ele){
int[] newArr = new int[elements.length + 1];
for (int i = 0;i < newArr.length;i++){
if (i < index){
newArr[i] = elements[i];
}else{
newArr[i + 1] = elements[i];
}
}
//Insert new element
newArr[index] = ele;
//Replace array
elements = newArr;
}
//Replace one of the elements
public void update(int index,int ele){
if (index < 0 || index > elements.length - 1){
throw new RuntimeException("The passed in subscript is incorrect. The array cannot be modified");
}
elements[index] = ele;
}
//Linear search
public int search(int target){
for (int i = 0;i < elements.length;i++){
if (elements[i] == target){
return i;
}
}
//Corresponding element not found
return -1;
}
}
Test array:
public class TestMyArray {
public static void main(String[] args) {
MyArray myArray = new MyArray();
myArray.add(2);
myArray.add(11);
myArray.add(15);
myArray.add(7);
myArray.add(14);
myArray.add(3);
myArray.add(8);
myArray.delete(2);
myArray.arrayShow();
}
}
3, Queue
1. Introduction
- Queue is a sequential list, which can be realized by array or linked list.
- Follow the principle of first in, first out. That is, the data stored in the queue should be taken out first. After the deposit, it shall be taken out
2. Code implementation
public class MyQueue {
//Create an array
int[] elements;
//Construction method
public MyQueue(){
elements = new int[0];
}
//Add element to queue
public void addQueue(int ele){
int[] newArr = new int[elements.length + 1];
for (int i = 0;i < elements.length;i++){
newArr[i] = elements[i];
}
newArr[elements.length] = ele;
elements = newArr;
}
//Fetch element from queue
public int getQueue(){
int ele = elements[0];
int[] newArr = new int[elements.length - 1];
for (int i = 0;i < newArr.length;i++){
newArr[i] = elements[i + 1];
}
elements = newArr;
return ele;
}
//Judge whether the queue is empty
public boolean isEmpty(){
return elements.length == 0;
}
//Query all elements
public void show(){
for (int i = 0;i < elements.length;i++){
System.out.println("Current queue No" + (i + 1) + "The first element is:" + elements[i]);
}
}
}
Testing.
public class TestMyQueue {
public static void main(String[] args) {
MyQueue mq = new MyQueue();
System.out.println("Is the queue empty:" + mq.isEmpty());
mq.addQueue(10);
System.out.println("Is the queue empty:" + mq.isEmpty());
mq.addQueue(12);
mq.addQueue(8);
mq.addQueue(15);
mq.addQueue(22);
mq.addQueue(113);
mq.show();
}
}
4, Linked list
1. Introduction
- Linked list is stored in the form of nodes, which is chain storage
- Each node contains data field and next field: point to the next node
- The nodes of the linked list are not necessarily stored continuously
2. One way linked list code implementation
public class SingleLinkedListDemo {
public static void main(String[] args) {
//Test
//Create node first
HeroNode hero1 = new HeroNode(1, "Song Jiang", "Timely rain");
HeroNode hero2 = new HeroNode(2, "Lu Junyi", "Jade Unicorn");
HeroNode hero3 = new HeroNode(3, "Wu Yong", "Zhiduoxing");
HeroNode hero4 = new HeroNode(4, "Lin Chong", "Leopard head");
//Create a linked list to
SingleLinkedList singleLinkedList = new SingleLinkedList();
//join
singleLinkedList.add(hero1);
singleLinkedList.add(hero4);
singleLinkedList.add(hero2);
singleLinkedList.add(hero3);
// Test the reverse function of the single linked list
System.out.println("The original linked list~~");
singleLinkedList.list();
// System.out.println("reverse single linked list ~ ~);
// reversetList(singleLinkedList.getHead());
// singleLinkedList.list();
System.out.println("Print single linked list in reverse order, The structure of the linked list has not been changed~~");
reversePrint(singleLinkedList.getHead());
/*
//Add in order of number
singleLinkedList.addByOrder(hero1);
singleLinkedList.addByOrder(hero4);
singleLinkedList.addByOrder(hero2);
singleLinkedList.addByOrder(hero3);
//Show one
singleLinkedList.list();
//Code for testing and modifying nodes
HeroNode newHeroNode = new HeroNode(2, "Xiao Lu "," Yu Qilin ~ ~ ");
singleLinkedList.update(newHeroNode);
System.out.println("Modified linked list ~ ~ ");
singleLinkedList.list();
//Delete a node
singleLinkedList.del(1);
singleLinkedList.del(4);
System.out.println("Deleted linked list ~ ~ ");
singleLinkedList.list();
//Test to find the number of effective nodes in the single linked list
System.out.println("Number of valid nodes = "+ getlength (singlelinkedlist. Gethead()); / / 2
//Test to see if you get the penultimate node
HeroNode res = findLastIndexNode(singleLinkedList.getHead(), 3);
System.out.println("res=" + res);
*/
}
//Mode 2:
//You can use the data structure of stack to press each node into the stack, and then use the first in and last out characteristics of stack to realize the effect of reverse order printing
public static void reversePrint(HeroNode head) {
if(head.next == null) {
return;//Empty linked list, cannot print
}
//To create a stack, press each node into the stack
Stack<HeroNode> stack = new Stack<HeroNode>();
HeroNode cur = head.next;
//Push all nodes of the linked list onto the stack
while(cur != null) {
stack.push(cur);
cur = cur.next; //cur moves backward so that the next node can be pushed in
}
//Print the nodes in the stack and pop them out of the stack
while (stack.size() > 0) {
System.out.println(stack.pop()); //stack is characterized by first in and last out
}
}
//Reverse single linked list
public static void reversetList(HeroNode head) {
//If the current linked list is empty or there is only one node, there is no need to reverse and return directly
if(head.next == null || head.next.next == null) {
return ;
}
//Define an auxiliary pointer (variable) to help us traverse the original linked list
HeroNode cur = head.next;
HeroNode next = null;// Points to the next node of the current node [cur]
HeroNode reverseHead = new HeroNode(0, "", "");
//Traverse the original linked list. Every time you traverse a node, take it out and put it at the front of the new linked list reverseHead
//Use your head
while(cur != null) {
next = cur.next;//First save the next node of the current node temporarily, because it needs to be used later
cur.next = reverseHead.next;//Point the next node of cur to the front of the new linked list
reverseHead.next = cur; //Connect cur to the new linked list
cur = next;//Move cur back
}
//Put head Next points to reversehead Next, realize the inversion of single linked list
head.next = reverseHead.next;
}
//Find the penultimate node in the single lin k ed list [Sina interview question]
//thinking
//1. Write a method to receive the head node and an index at the same time
//2. index indicates the penultimate node
//3. Traverse the linked list from beginning to end to get the total length of the linked list getLength
//4. After getting the size, we can get it by traversing the first size index in the linked list
//5. If it is found, the node will be returned; otherwise, nulll will be returned
public static HeroNode findLastIndexNode(HeroNode head, int index) {
//Judge if the linked list is empty, return null
if(head.next == null) {
return null;//Can't find
}
//The first traversal obtains the length of the linked list (number of nodes)
int size = getLength(head);
//The second time we traverse the size index position is the K-th node from the bottom
//First do an index check
if(index <=0 || index > size) {
return null;
}
//Defined to the auxiliary variable, the for loop locates the index of the reciprocal
HeroNode cur = head.next; //3 // 3 - 1 = 2
for(int i =0; i< size - index; i++) {
cur = cur.next;
}
return cur;
}
//Method: obtain the number of nodes in the single linked list (if it is the linked list of the leading node, the head node shall not be counted)
/**
*
* @param head Head node of linked list
* @return Returns the number of valid nodes
*/
public static int getLength(HeroNode head) {
if(head.next == null) { //Empty linked list
return 0;
}
int length = 0;
//Define an auxiliary variable. Here we do not have a statistical header node
HeroNode cur = head.next;
while(cur != null) {
length++;
cur = cur.next; //ergodic
}
return length;
}
}
//Define SingleLinkedList to manage our heroes
class SingleLinkedList {
//First initialize a head node. The head node does not move and does not store specific data
private HeroNode head = new HeroNode(0, "", "");
//Return header node
public HeroNode getHead() {
return head;
}
//Add node to one-way linked list
//Train of thought, when the numbering sequence is not considered
//1. Find the last node of the current linked list
//2. Point the next of the last node to the new node
public void add(HeroNode heroNode) {
//Because the head node cannot be moved, we need an auxiliary traversal temp
HeroNode temp = head;
//Traverse the linked list to find the last
while(true) {
//Find the end of the linked list
if(temp.next == null) {//
break;
}
//If the last is not found, move temp back
temp = temp.next;
}
//When exiting the while loop, temp points to the end of the linked list
//Point the next of the last node to the new node
temp.next = heroNode;
}
//The second way is to insert the hero into the specified position according to the ranking when adding the hero
//(if there is this ranking, the addition fails and a prompt is given)
public void addByOrder(HeroNode heroNode) {
//Because the head node cannot be moved, we still use an auxiliary pointer (variable) to help find the added position
//Because of the single linked list, because the temp we are looking for is the previous node in the add location, otherwise it cannot be inserted
HeroNode temp = head;
boolean flag = false; // Whether the number added by flag flag exists. The default is false
while(true) {
if(temp.next == null) {//Note that temp is at the end of the linked list
break; //
}
if(temp.next.no > heroNode.no) { //If the location is found, insert it after temp
break;
} else if (temp.next.no == heroNode.no) {//Indicates that the number of the heroNode you want to add already exists
flag = true; //Description number exists
break;
}
temp = temp.next; //Move back and traverse the current linked list
}
//Judge the value of flag
if(flag) { //Cannot add, description number exists
System.out.printf("The number of the hero to insert %d It already exists, Can't join\n", heroNode.no);
} else {
//Insert it into the linked list, after temp
heroNode.next = temp.next;
temp.next = heroNode;
}
}
//Modify the node information according to the no number, that is, the no number cannot be changed
//explain
//1. Modify according to the no of newHeroNode
public void update(HeroNode newHeroNode) {
//Judge whether it is empty
if(head.next == null) {
System.out.println("The linked list is empty~");
return;
}
//Find the node to be modified and number it according to no
//Define an auxiliary variable
HeroNode temp = head.next;
boolean flag = false; //Indicates whether the node is found
while(true) {
if (temp == null) {
break; //The linked list has been traversed
}
if(temp.no == newHeroNode.no) {
//find
flag = true;
break;
}
temp = temp.next;
}
//Judge whether to find the node to be modified according to the flag
if(flag) {
temp.name = newHeroNode.name;
temp.nickname = newHeroNode.nickname;
} else { //Can't find
System.out.printf("No number found %d The node cannot be modified\n", newHeroNode.no);
}
}
//Delete node
//thinking
//1. The head cannot be moved, so we need a temp auxiliary node to find the previous node of the node to be deleted
//2. Explain that when we compare, it is temp next. Comparison between NO and no of the node to be deleted
public void del(int no) {
HeroNode temp = head;
boolean flag = false; // Flag whether the node to be deleted is found
while(true) {
if(temp.next == null) { //It has reached the end of the linked list
break;
}
if(temp.next.no == no) {
//Found the previous node temp of the node to be deleted
flag = true;
break;
}
temp = temp.next; //temp backward, traversal
}
//Judge flag
if(flag) { //find
//Can delete
temp.next = temp.next.next;
}else {
System.out.printf("To delete %d Node does not exist\n", no);
}
}
//Display linked list [traversal]
public void list() {
//Judge whether the linked list is empty
if(head.next == null) {
System.out.println("The linked list is empty");
return;
}
//Because the head node cannot be moved, we need an auxiliary variable to traverse
HeroNode temp = head.next;
while(true) {
//Judge whether to reach the end of the linked list
if(temp == null) {
break;
}
//Output node information
System.out.println(temp);
//Move temp backward. Be careful
temp = temp.next;
}
}
}
//Define a HeroNode. Each HeroNode object is a node
class HeroNode {
public int no;
public String name;
public String nickname;
public HeroNode next; //Point to next node
//constructor
public HeroNode(int no, String name, String nickname) {
this.no = no;
this.name = name;
this.nickname = nickname;
}
//To display the method, we re toString
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + ", nickname=" + nickname + "]";
}
}
3. Code implementation of bidirectional linked list
public class DoubleLinkedListDemo {
public static void main(String[] args) {
// test
System.out.println("Test of bidirectional linked list");
// Create node first
HeroNode2 hero1 = new HeroNode2(1, "Song Jiang", "Timely rain");
HeroNode2 hero2 = new HeroNode2(2, "Lu Junyi", "Jade Unicorn");
HeroNode2 hero3 = new HeroNode2(3, "Wu Yong", "Zhiduoxing");
HeroNode2 hero4 = new HeroNode2(4, "Lin Chong", "Leopard head");
// Create a two-way linked list
DoubleLinkedList doubleLinkedList = new DoubleLinkedList();
doubleLinkedList.add(hero1);
doubleLinkedList.add(hero2);
doubleLinkedList.add(hero3);
doubleLinkedList.add(hero4);
doubleLinkedList.list();
// modify
HeroNode2 newHeroNode = new HeroNode2(4, "Gongsun Sheng", "Ru Yunlong");
doubleLinkedList.update(newHeroNode);
System.out.println("Modified linked list");
doubleLinkedList.list();
// delete
doubleLinkedList.del(3);
System.out.println("Linked list after deletion~~");
doubleLinkedList.list();
}
}
// Create a class of two-way linked list
class DoubleLinkedList {
// First initialize a head node. The head node does not move and does not store specific data
private HeroNode2 head = new HeroNode2(0, "", "");
// Return header node
public HeroNode2 getHead() {
return head;
}
// Method of traversing bidirectional linked list
// Display linked list [traversal]
public void list() {
// Determine whether the linked list is empty
if (head.next == null) {
System.out.println("The linked list is empty");
return;
}
// Because the head node cannot be moved, we need an auxiliary variable to traverse
HeroNode2 temp = head.next;
while (true) {
// Judge whether to reach the end of the linked list
if (temp == null) {
break;
}
// Output node information
System.out.println(temp);
// Move temp backward. Be careful
temp = temp.next;
}
}
// Add a node to the end of the bidirectional linked list
public void add(HeroNode2 heroNode) {
// Because the head node cannot be moved, we need an auxiliary traversal temp
HeroNode2 temp = head;
// Traverse the linked list to find the last
while (true) {
// Find the end of the linked list
if (temp.next == null) {//
break;
}
// If the last is not found, move temp back
temp = temp.next;
}
// When exiting the while loop, temp points to the end of the linked list
// Form a two-way linked list
temp.next = heroNode;
heroNode.pre = temp;
}
// When modifying the content of a node, you can see that the node content modification of the two-way linked list is the same as that of the one-way linked list
// Only the node type is changed to HeroNode2
public void update(HeroNode2 newHeroNode) {
// Judge whether it is empty
if (head.next == null) {
System.out.println("The linked list is empty~");
return;
}
// Find the node to be modified and number it according to no
// Define an auxiliary variable
HeroNode2 temp = head.next;
boolean flag = false; // Indicates whether the node is found
while (true) {
if (temp == null) {
break; // The linked list has been traversed
}
if (temp.no == newHeroNode.no) {
// find
flag = true;
break;
}
temp = temp.next;
}
// Judge whether to find the node to be modified according to the flag
if (flag) {
temp.name = newHeroNode.name;
temp.nickname = newHeroNode.nickname;
} else { // Can't find
System.out.printf("No number found %d The node cannot be modified\n", newHeroNode.no);
}
}
// Delete a node from the two-way linked list,
// explain
// 1 for a two-way linked list, we can directly find the node to be deleted
// 2. After finding it, delete it by yourself
public void del(int no) {
// Judge whether the current linked list is empty
if (head.next == null) {// Empty linked list
System.out.println("The linked list is empty and cannot be deleted");
return;
}
HeroNode2 temp = head.next; // Auxiliary variable (pointer)
boolean flag = false; // Flag whether the node to be deleted is found
while (true) {
if (temp == null) { // It has reached the end of the linked list
break;
}
if (temp.no == no) {
// Found the previous node temp of the node to be deleted
flag = true;
break;
}
temp = temp.next; // temp backward, traversal
}
// Judge flag
if (flag) { // find
// Can delete
// temp.next = temp.next.next; [one way linked list]
temp.pre.next = temp.next;
// What's wrong with our code here?
// If it is the last node, you do not need to execute the following sentence, otherwise a null pointer will appear
if (temp.next != null) {
temp.next.pre = temp.pre;
}
} else {
System.out.printf("To delete %d Node does not exist\n", no);
}
}
}
// Define HeroNode2. Each HeroNode object is a node
class HeroNode2 {
public int no;
public String name;
public String nickname;
public HeroNode2 next; // Point to the next node, which is null by default
public HeroNode2 pre; // Point to the previous node, which is null by default
// constructor
public HeroNode2(int no, String name, String nickname) {
this.no = no;
this.name = name;
this.nickname = nickname;
}
// To display the method, we re toString
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + ", nickname=" + nickname + "]";
}
}
5, Stack
1. Introduction
-
A stack is an ordered list of Filo first in last out.
-
Stack is a special linear table that restricts the insertion and deletion of elements in a linear table to the same end of the linear table. The end that allows insertion and deletion is the changing end
It is called the top of the stack, and the other end is the fixed end, which is called the bottom of the stack.
-
According to the definition of stack, the first element put into the stack is at the bottom of the stack, the last element put into the stack is at the top of the stack, while the deleted element is just the opposite. The last element put into the stack is deleted first, and the first element is deleted last
2. Code implementation
public class MyStack {
//Use arrays to store stacks
private int[] elements;
//Construction method
public MyStack(){
elements = new int[0];
}
//Get array length
public int size(){
return elements.length;
}
//Push in element
public void push(int ele){
//Create a new array
int[] newArr = new int[elements.length + 1];
//Add the original array element to the new array
for (int i = 0;i < elements.length;i++){
newArr[i] = elements[i];
}
//Add new element to new array
newArr[elements.length] = ele;
//The new array is assigned to the old array
elements = newArr;
}
//Take out the top element of the stack
public int pop(){
//Throw exception if stack is empty
if (elements.length == 0){
throw new RuntimeException("No data in stack,Cannot eject element");
}
//New array
int[] newArr = new int[elements.length - 1];
//Put elements into a new array
for (int i = 0;i < newArr.length;i++){
newArr[i] = elements[i];
}
//Take out the top element of the stack first
int ele = elements[elements.length - 1];
//Assign to the original array
elements = newArr;
//Return stack top element
return ele;
}
//View stack top element
public int showPeek(){
//Throw exception if stack is empty
if (elements.length == 0){
throw new RuntimeException("No data in stack,Cannot view stack top element");
}
return elements[elements.length - 1];
}
//Determine whether the stack is empty
public boolean isEmpty(){
return elements.length == 0;
}
}
Testing.
public class TestMyStack {
public static void main(String[] args) {
MyStack myStack = new MyStack();
myStack.push(10);
myStack.push(20);
myStack.push(30);
System.out.println(myStack.isEmpty());
System.out.println(myStack.showPeek());
System.out.println(myStack.pop());
System.out.println(myStack.showPeek());
System.out.println(myStack.pop());
System.out.println(myStack.showPeek());
System.out.println(myStack.pop());
System.out.println(myStack.isEmpty());
}
}
6, Recursion
1. Introduction
Recursion is a method that calls itself and passes in different variables each time Recursion helps programmers solve complex problems and makes code concise.
2. Common code implementation
public class TestRecursive {
public static void main(String[] args) {
show(10);
}
public static void show(int i){
if (i > 0){
System.out.println(i);
show(--i);
}
}
}
3. Implementation of Hanoi Tower problem
public class TestHanoi {
public static void main(String[] args) {
hanoi(3,'A','B','C');
}
/**
* Hanoi Tower completion logic
* @param n How many plates are there altogether
* @param start Starting position
* @param middle Conversion position
* @param end Target location
*/
public static void hanoi(int n,char start,char middle,char end){
if (n == 1){
System.out.println("Remove the first plate from the" + start + "Move to" + end);
}
else{
//Remove all the plates on the last one
hanoi(n - 1,start,end,middle);
System.out.println("The first" + n + "A plate from" + start + "Move to" + end);
hanoi(n-1,middle,start,end);
}
}
}
4. Implementation of Fibonacci sequence problem
public class TestFebonacci {
public static void main(String[] args) {
System.out.println(febonacci(8));
}
public static int febonacci(int i) {
if (i == 1 || i == 2){
return 1;
}
return febonacci(i - 1) + febonacci(i - 2);
}
}
7, Tree
1. Introduction
Tree is a nonlinear data structure. It is a set with hierarchical relationship composed of n (n > = 0) finite nodes. It is called a tree because it looks like an upside down tree, that is, it has its roots up and its leaves down.
- Root node: the root node has no precursor node.
- Except for the root node, the other nodes are divided into a subtree with a structure similar to that of the tree. The root node of each subtree has and has only one precursor, which can have 0 or more successors.
- Therefore, the tree is recursively defined.
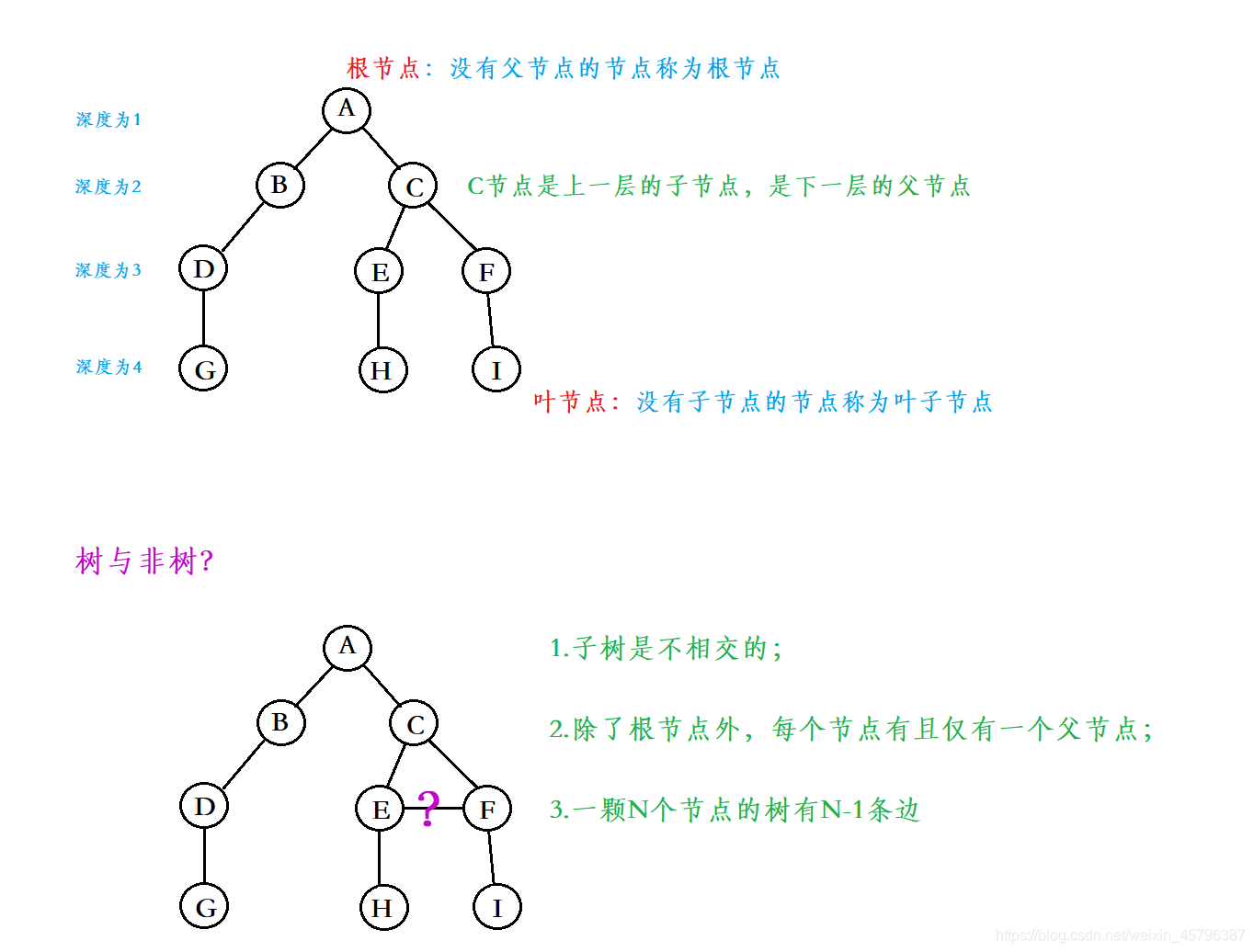
2. Several common concepts
- Degree of node: the number of subtrees contained in a node is called the degree of the node; As shown in the figure above: A is 2
- Leaf node: a node with a degree of 0 is called a leaf node; As shown in the figure above, nodes G, H and I are leaf nodes
- Non terminal node or branch node: a node whose degree is not 0; As shown in the figure above, nodes B, D, C, E and F are branch nodes
- Parent node or parent node: if a node contains child nodes, this node is called the parent node of its child nodes; As shown in the figure above: A is the parent node of B
- Child node or child node: the root node of the subtree contained in a node is called the child node of the node; As shown in the figure above: B is the child node of A
- Sibling node: nodes with the same parent node are called sibling nodes; As shown in the figure above: B and C are sibling nodes
- Tree degree: the degree of the largest node in a tree is called the degree of the tree; As shown in the figure above: the degree of the tree is 2
- Hierarchy of nodes: defined from the root, the root is the first layer, and the child nodes of the root are the second layer, and so on;
- Height or depth of tree: the maximum level of nodes in the tree; As shown in the figure above: the height of the tree is 4
- Cousin node: nodes with parents on the same layer are cousins to each other; As shown in the figure above, H and I are brother nodes of each other
- Ancestor of a node: all nodes from the root to the branch through which the node passes; As shown in the figure above: A is the ancestor of all nodes
- Descendant: any node in the subtree with a node as the root is called the descendant of the node. As shown in the figure above: all nodes are descendants of A
- Forest: a collection of m disjoint trees is called forest;
3. Binary tree
3.1 introduction
A binary tree is a finite set of nodes. The set is either empty or composed of a root node plus two binary trees called left subtree and right subtree.
Characteristics of binary tree:
- Each node has at most two subtrees, that is, the binary tree does not have nodes with a degree greater than 2.
- The subtree of a binary tree can be divided into left and right, and the order of its subtrees cannot be reversed.
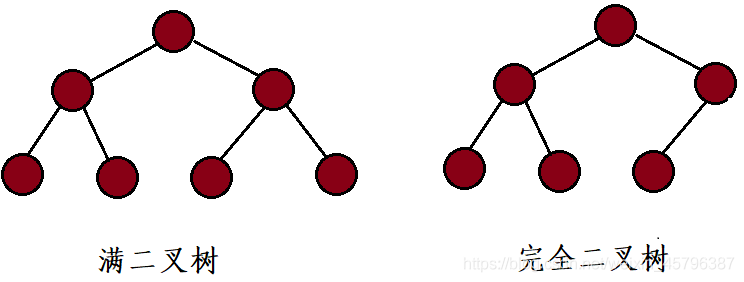
3.2 storage structure
There are two kinds of sequential storage structures: one is the sequential tree structure, and the other is the sequential tree structure.
3.3 linked storage binary tree
Code implementation:
Create node code:
public class TreeNode {
//Node three elements
private Integer value;
private TreeNode leftNode;
private TreeNode rightNode;
//Initializing a node requires assigning a value to it
public TreeNode(Integer value) {
this.value = value;
}
//Assign values to elements
public void setLeftNode(TreeNode leftNode) {
this.leftNode = leftNode;
}
public void setRightNode(TreeNode rightNode) {
this.rightNode = rightNode;
}
public Integer getValue() {
return value;
}
public void setValue(Integer value) {
this.value = value;
}
//Preorder traversal
public void frontShow(){
System.out.println(value);
if (leftNode != null){
leftNode.frontShow();
}
if (rightNode != null){
rightNode.frontShow();
}
}
//Middle order traversal
public void midShow(){
if (leftNode != null){
leftNode.midShow();
}
System.out.println(value);
if (rightNode != null){
rightNode.midShow();
}
}
//Postorder traversal
public void afterShow(){
if (leftNode != null){
leftNode.afterShow();
}
if (rightNode != null){
rightNode.afterShow();
}
System.out.println(value);
}
//Preorder search
public TreeNode frontSearch(int num){
TreeNode target = null;
if (value == num){
return this;
}else{
if (leftNode != null){
target = leftNode.frontSearch(num);
}
if (target != null){
return target;
}
if (rightNode != null){
target = rightNode.frontSearch(num);
}
}
return target;
}
@Override
public String toString() {
return "TreeNode{" +
"value=" + value +
", leftNode=" + leftNode +
", rightNode=" + rightNode +
'}';
}
//Delete subtree
public void delete(int num){
TreeNode parent = this;
if (parent.leftNode != null && parent.leftNode.value == num){
parent.leftNode = null;
return;
}
if (parent.rightNode != null && parent.rightNode.value == null){
parent.rightNode = null;
return;
}
parent = leftNode;
if (parent != null){
leftNode.delete(num);
};
parent = rightNode;
if (parent != null){
rightNode.delete(num);
}
}
}
Code for creating binary tree:
public class BinaryTree {
TreeNode root;
//The root node of the binary tree should be set
public TreeNode getRoot() {
return root;
}
public void setRoot(TreeNode root) {
this.root = root;
}
public void frontShow(){
root.frontShow();
}
public void midShow(){
root.midShow();
}
public void afterShow(){
root.afterShow();
}
public TreeNode frontSearch(int num){
return root.frontSearch(num);
}
public void delete(int num){
root.delete(num);
}
}
Test:
public class TestBinaryTree {
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
TreeNode node_01_01 = new TreeNode(1);
//The tree has a root node set
tree.setRoot(node_01_01);
TreeNode node_02_02 = new TreeNode(2);
TreeNode node_02_03 = new TreeNode(3);
node_01_01.setLeftNode(node_02_02);
node_01_01.setRightNode(node_02_03);
TreeNode node_03_04 = new TreeNode(4);
TreeNode node_03_05 = new TreeNode(5);
TreeNode node_03_06 = new TreeNode(6);
TreeNode node_03_07 = new TreeNode(7);
node_02_02.setLeftNode(node_03_04);
node_02_02.setRightNode(node_03_05);
node_02_03.setLeftNode(node_03_06);
node_02_03.setRightNode(node_03_07);
TreeNode node_04_08 = new TreeNode(8);
TreeNode node_04_09 = new TreeNode(9);
TreeNode node_04_10 = new TreeNode(10);
TreeNode node_04_11 = new TreeNode(11);
TreeNode node_04_12 = new TreeNode(12);
TreeNode node_04_13 = new TreeNode(13);
TreeNode node_04_14 = new TreeNode(14);
TreeNode node_04_15 = new TreeNode(15);
node_03_04.setLeftNode(node_04_08);
node_03_04.setRightNode(node_04_09);
node_03_05.setLeftNode(node_04_10);
node_03_05.setRightNode(node_04_11);
node_03_06.setLeftNode(node_04_12);
node_03_06.setRightNode(node_04_13);
node_03_07.setLeftNode(node_04_14);
node_03_07.setRightNode(node_04_15);
tree.delete(5);
tree.frontShow();
}
}
3.4 sequential storage binary tree
In fact, every binary tree can be transformed into an array, and an array can also be transformed into a binary tree. However, only the case of complete binary tree is generally considered, because in other cases, there may be null values in the middle of the array.
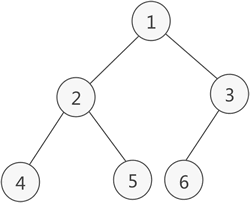
The above binary tree can be changed into the following array:

In this way, the subscript can be inferred from the above binary tree:
- If the parent node subscript is n, its left child node subscript (2n+1)
- If the subscript of the parent node is n, its right child node subscript (2n+2)
- If the child node subscript is n, its parent node subscript is (n-1)/2
Code implementation:
public class ArrayBinaryTree {
int[] data;
public ArrayBinaryTree(int[] data) {
this.data = data;
}
public void frontShow(){
frontShow(0);
}
public void frontShow(int index){
if (data == null || data.length == 0){
return;
}
//First traverse the contents of the current node
System.out.println(data[index]);
if (2*index + 1 < data.length){
frontShow(2*index + 1);
}
if (2*index + 2 < data.length){
frontShow(2*index + 2);
}
}
}
Output the value of the corresponding subscript:
public class TestArrayBinaryTree {
public static void main(String[] args) {
int[] array = new int[]{1,2,3,5,7,11,14,145};
ArrayBinaryTree tree = new ArrayBinaryTree(array);
tree.frontShow(7);
}
}
4. Clue binary tree
Node:
public class ThreadedNode {
//Weight of node
int value;
//Left son
ThreadedNode leftNode;
//Right son
ThreadedNode rightNode;
//Identify pointer type
int leftType;
int rightType;
public ThreadedNode(int value) {
this.value=value;
}
//Set left son
public void setLeftNode(ThreadedNode leftNode) {
this.leftNode = leftNode;
}
//Set right son
public void setRightNode(ThreadedNode rightNode) {
this.rightNode = rightNode;
}
//Preorder traversal
public void frontShow() {
//First traverse the contents of the current node
System.out.println(value);
//Left node
if(leftNode!=null) {
leftNode.frontShow();
}
//Right node
if(rightNode!=null) {
rightNode.frontShow();
}
}
//Middle order traversal
public void midShow() {
//Left child node
if(leftNode!=null) {
leftNode.midShow();
}
//Current node
System.out.println(value);
//Right child node
if(rightNode!=null) {
rightNode.midShow();
}
}
//Postorder traversal
public void afterShow() {
//Left child node
if(leftNode!=null) {
leftNode.afterShow();
}
//Right child node
if(rightNode!=null) {
rightNode.afterShow();
}
//Current node
System.out.println(value);
}
//Preorder search
public ThreadedNode frontSearch(int i) {
ThreadedNode target=null;
//Compare the values of the current node
if(this.value==i) {
return this;
//The value of the current node is not the node to find
}else {
//Find left son
if(leftNode!=null) {
//It may or may not be found. If not, the target is still null
target = leftNode.frontSearch(i);
}
//If it is not empty, it indicates that it has been found in the left son
if(target!=null) {
return target;
}
//Find right son
if(rightNode!=null) {
target=rightNode.frontSearch(i);
}
}
return target;
}
//Delete a subtree
public void delete(int i) {
ThreadedNode parent = this;
//Judge left son
if(parent.leftNode!=null&&parent.leftNode.value==i) {
parent.leftNode=null;
return;
}
//Judge right son
if(parent.rightNode!=null&&parent.rightNode.value==i) {
parent.rightNode=null;
return;
}
//Recursively check and delete the left column
parent=leftNode;
if(parent!=null) {
parent.delete(i);
}
//Recursively check and delete the right son
parent=rightNode;
if(parent!=null) {
parent.delete(i);
}
}
}
Implementation code of tree:
public class ThreadedBinaryTree {
ThreadedNode root;
//Precursor node for temporary storage
ThreadedNode pre=null;
//Traversal clue binary tree
public void threadIterate() {
//Used to temporarily store the current traversal node
ThreadedNode node = root;
while(node!=null) {
//Loop to find the first node
while(node.leftType==0) {
node=node.leftNode;
}
//Print the value of the current node
System.out.println(node.value);
//If the right pointer of the current node points to the successor node, the successor node may also have successor nodes
while(node.rightType==1) {
node=node.rightNode;
System.out.println(node.value);
}
//Replace traversed nodes
node=node.rightNode;
}
}
//Set root node
public void setRoot(ThreadedNode root) {
this.root = root;
}
//Medium order cued binary tree
public void threadNodes() {
threadNodes(root);
}
public void threadNodes(ThreadedNode node) {
//If the current node is null, it will be returned directly
if(node==null) {
return;
}
//Processing left subtree
threadNodes(node.leftNode);
//Processing precursor nodes
if(node.leftNode==null){
//Make the left pointer of the current node point to the predecessor node
node.leftNode=pre;
//Change the type of the left pointer of the current node
node.leftType=1;
}
//Handle the right pointer of the precursor. If the right pointer of the precursor node is null (there is no lower right subtree)
if(pre!=null&&pre.rightNode==null) {
//Let the right pointer of the predecessor node point to the current node
pre.rightNode=node;
//Change the right pointer type of the precursor node
pre.rightType=1;
}
//Each time a node is processed, the current node is the precursor node of the next node
pre=node;
//Processing right subtree
threadNodes(node.rightNode);
}
//Get root node
public ThreadedNode getRoot() {
return root;
}
//Preorder traversal
public void frontShow() {
if(root!=null) {
root.frontShow();
}
}
//Middle order traversal
public void midShow() {
if(root!=null) {
root.midShow();
}
}
//Postorder traversal
public void afterShow() {
if(root!=null) {
root.afterShow();
}
}
//Preorder search
public ThreadedNode frontSearch(int i) {
return root.frontSearch(i);
}
//Delete subtree
public void delete(int i) {
if(root.value==i) {
root=null;
}else {
root.delete(i);
}
}
}
Test:
public class TestThreadedBinaryTree {
public static void main(String[] args) {
//Create a tree
ThreadedBinaryTree binTree = new ThreadedBinaryTree();
//Create a root node
ThreadedNode root = new ThreadedNode(1);
//Assign root node to tree
binTree.setRoot(root);
//Create a left node
ThreadedNode rootL = new ThreadedNode(2);
//Set the newly created node as the child of the root node
root.setLeftNode(rootL);
//Create a right node
ThreadedNode rootR = new ThreadedNode(3);
//Set the newly created node as the child of the root node
root.setRightNode(rootR);
//Create two child nodes for the left node of the second layer
rootL.setLeftNode(new ThreadedNode(4));
ThreadedNode fiveNode = new ThreadedNode(5);
rootL.setRightNode(fiveNode);
//Create two child nodes for the right node of the second layer
rootR.setLeftNode(new ThreadedNode(6));
rootR.setRightNode(new ThreadedNode(7));
//Middle order traversal tree
binTree.midShow();
System.out.println("===============");
//Middle front cable binary tree
binTree.threadNodes();
binTree.threadIterate();
}
}
5. Huffman tree
5.1 introduction
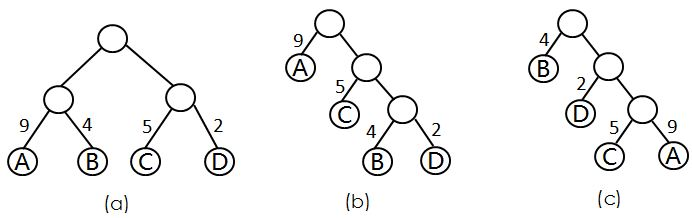
Weighted path of leaf node: as shown in the above figure, the line segment on each node (A/B/C/D) has a number, which is the weight. The weighted path is the weight of several such line segments.
For example, the weighted path of a in figure (a) is 9 × 2 = 18, the weighted path of B is 4 × 2 = 8.
Weighted path length of tree WPL: it is the sum of weighted paths of all leaf nodes of a tree.
Then calculate:
(a) WPL in Figure: 9 × 2 + 4 × 2 + 5 × 2 + 2 × 2 = 40
(b) WPL in Figure: 9 × 1 + 5 × 2 + 4 × 3 + 2 × 3 = 37
(c) WPL in the figure: 4 × 1 + 2 × 2 + 5 × 3 +9 × 3 =50
When trying to build a tree with n nodes (all leaf nodes and each has its own weight), if the weighted path length (WPL) of the tree is the smallest, the tree is called "optimal binary tree", sometimes called "Huffman tree" or "Huffman tree". That is, b is the Huffman tree.
5.2 theoretical realization
For a given n nodes with respective weights, there is an effective way to build Huffman tree:
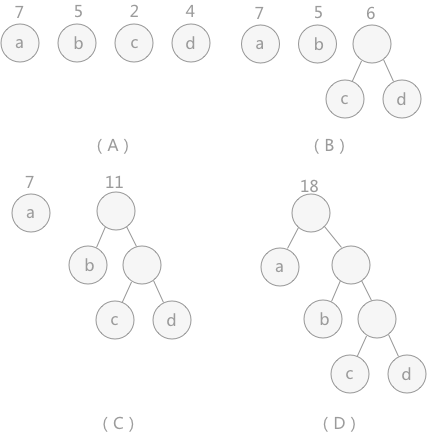
- The two smallest weights are selected from the n weights, and the corresponding two nodes form a new binary tree, and the weight of the root node of the new binary tree is the sum of the weight of the left and right children;
- Delete the two smallest weights from the original n weights, and add the new weights to the ranks of n – 2 weights, and so on;
- Repeat 1 and 2 until all nodes form a binary tree, which is the Huffman tree.
5.3 code implementation
Create node:
public class Node implements Comparable<Node> {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
@Override
public int compareTo(Node o) {
return -(this.value - o.value);
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
}
Huffman tree:
public class TestHuffmanTree {
public static void main(String[] args) {
int[] arr = {3,7,8,29,5,11,23,14};
Node node = createHuffmanTree(arr);
System.out.println(node);
}
//Create Huffman tree
public static Node createHuffmanTree(int[] arr) {
//First, use all the elements in the array to create several binary trees (only one node)
List<Node> nodes = new ArrayList<>();
for(int value:arr) {
nodes.add(new Node(value));
}
//Cyclic processing,
while(nodes.size()>1) {
//sort
Collections.sort(nodes);
//Take out the two binary trees with the smallest weight
//Take out the binary tree with the smallest weight
Node left = nodes.get(nodes.size()-1);
//Take out the binary tree with the smallest weight
Node right = nodes.get(nodes.size()-2);
//Create a new binary tree
Node parent = new Node(left.value+right.value);
//Remove the two binary trees
nodes.remove(left);
nodes.remove(right);
//Put it into the original binary tree set
nodes.add(parent);
}
return nodes.get(0);
}
}
5.4 Huffman coding
For example, to pass a statement like can you can a can as a can canner can a can
If we directly encode each word according to the previous coding form, we will see a very large binary bytecode.
Here's what happens first:
99 97 110 32 121 111 117 32 99 97 110 32 97 32 99 97 110 32 97 115 32 97 32 99 97 110 32 99 97 110 110 101 114 32 99 97 110 32 97 32 99 97 110 46
Then it becomes like this: the total length is 396
01100011 01100001 01101110 00100000 01111001 01101111 01110101 00100000 01100011 01100001 01101110 00100000 01100001 00100000 01100011 01100001 01101110 00100000 01100001 01110011 00100000 01100001 00100000 01100011 01100001 01101110 00100000 01100011 01100001 01101110 01101110 01100101 01110010 00100000 01100011 01100001 01101110 00100000 01100001 00100000 01100011 01100001 01101110 00101110
There is too much storage in this way. It's hard to eat memory.
Then some people think it's better to change the way:
First record the number of times each letter appears: R: 1 s: 1 u: 1 E: 1 y: 1 1 o: 1 C: 7 n: 8 space: 11 a:11
Then we can solve this problem by representing the most letters with smaller numbers and the less letters with larger numbers.
For example, according to this logic: 0=a,1 = space, 10 = n, 11 = C, 100 = O, 101 =, 110=y,111=e,1000=u,1001=s,1010=r
Then it becomes this form: 11 0 10 1 110 100 11010111001010011
The actual bytecode has no spaces: 11010111010011010111001010011
In this way, there is another question. How to break a sentence? Is the first one 1, 11 or 110?
At this time, Huffman tree can be used to store. As shown below:
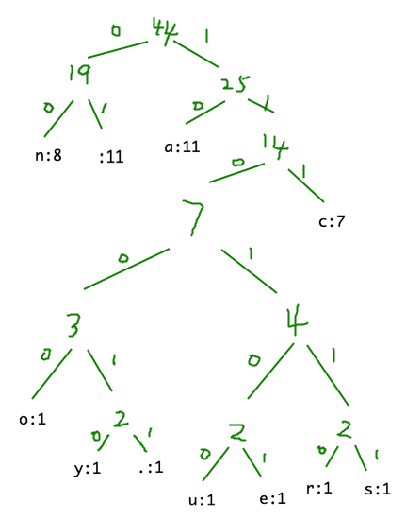
Then the code of each character can be stored according to the above weight.

This ensures the uniqueness of the data.
The saved character codes are as follows:
111 10 00 01 110010 11000 110100 01 111 10 00 01 10 01 111 10 00 01 10 110111 01 10 01 111 10 00 01 111 10 00 00 110101 110110 01 111 10 00 01 10 01 111 10 00 110011
Remove the space: the total length is 122
11110000111001011000110100011111000011001111100001101101110110011111000011111000001101011101100111110000110011111000110011
From 396 to 122, it can be seen that there is a lot of compression.
Code implementation:
It should be divided into the following steps:
-
Count the number of characters and sort
-
Create Huffman tree
-
Create Huffman coding table
-
code
Create node:
public class Node implements Comparable<Node> {
Byte data;
int weight;
Node left;
Node right;
public Node(Byte data,int weight) {
this.data=data;
this.weight=weight;
}
@Override
public String toString() {
return "Node [data=" + data + ", weight=" + weight + "]";
}
@Override
public int compareTo(Node o) {
return o.weight-this.weight;
}
}
Create Huffman tree:
public class TestHuffmanCode {
public static void main(String[] args) {
// String msg="can you can a can as a can canner can a can.";
// byte[] bytes = msg.getBytes();
// //Huffman coding compression
// byte[] b = huffmanZip(bytes);
// //Decoding using Huffman coding
// byte[] newBytes = decode(huffCodes,b);
// System.out.println(new String(newBytes));
String src="1.bmp";
String dst="2.zip";
// try {
// zipFile(src, dst);
// } catch (IOException e) {
// e.printStackTrace();
// }
try {
unZip("2.zip", "3.bmp");
} catch (Exception e) {
e.printStackTrace();
}
}
/**
* File decompression
* @param src
* @param dst
* @throws Exception
*/
public static void unZip(String src,String dst) throws Exception {
//Create an input stream
InputStream is = new FileInputStream("2.zip");
ObjectInputStream ois = new ObjectInputStream(is);
//Read byte array
byte[] b = (byte[]) ois.readObject();
//Read Huffman coding table
Map<Byte, String> codes = (Map<Byte, String>) ois.readObject();
ois.close();
is.close();
//decode
byte[] bytes = decode(codes, b);
//Create an output stream
OutputStream os = new FileOutputStream(dst);
//Write data
os.write(bytes);
os.close();
}
/**
* Compressed file
* @param src
* @param dst
* @throws IOException
*/
public static void zipFile(String src,String dst) throws IOException {
//Create an input stream
InputStream is = new FileInputStream(src);
//Create a byte array with the same size as the file pointed to by the input stream
byte[] b = new byte[is.available()];
//Read file contents
is.read(b);
is.close();
//Coding using Huffman coding
byte[] byteZip = huffmanZip(b);
//Output stream
OutputStream os = new FileOutputStream(dst);
ObjectOutputStream oos = new ObjectOutputStream(os);
//Write the compressed byte array to the file
oos.writeObject(byteZip);
//Write Huffman coding table to file
oos.writeObject(huffCodes);
oos.close();
os.close();
}
/**
* Decode using the specified Huffman encoding table
* @param huffCodes2
* @param b
* @return
*/
private static byte[] decode(Map<Byte, String> huffCodes, byte[] bytes) {
StringBuilder sb = new StringBuilder();
//Convert byte array into a binary string
for(int i=0;i<bytes.length;i++) {
byte b = bytes[i];
//Is it the last one.
boolean flag = (i==bytes.length-1);
sb.append(byteToBitStr(!flag,b));
}
//Decode the string according to the specified Huffman encoding
//Exchange the key value pairs encoded by Huffman
Map<String, Byte> map = new HashMap<>();
for(Map.Entry<Byte, String> entry:huffCodes.entrySet()) {
map.put(entry.getValue(), entry.getKey());
}
//Create a collection for storing byte s
List<Byte> list = new ArrayList<>();
//Processing string
for(int i=0;i<sb.length();) {
int count=1;
boolean flag = true;
Byte b=null;
//Intercept a byte
while(flag) {
String key = sb.substring(i, i+count);
b = map.get(key);
if(b==null) {
count++;
}else {
flag=false;
}
}
list.add(b);
i+=count;
}
//Convert a set to an array
byte[] b = new byte[list.size()];
for(int i=0;i<b.length;i++) {
b[i]=list.get(i);
}
return b;
}
private static String byteToBitStr(boolean flag,byte b) {
int temp=b;
if(flag) {
temp|=256;
}
String str = Integer.toBinaryString(temp);
if(flag) {
return str.substring(str.length()-8);
}else {
return str;
}
}
/**
* Method of Huffman coding compression
* @param bytes
* @return
*/
private static byte[] huffmanZip(byte[] bytes) {
//First count the number of occurrences of each byte and put it into a collection
List<Node> nodes = getNodes(bytes);
//Create a Huffman tree
Node tree = createHuffmanTree(nodes);
//Create a Huffman coding table
Map<Byte, String> huffCodes = getCodes(tree);
//code
byte[] b = zip(bytes,huffCodes);
return b;
}
/**
* Huffman coding
* @param bytes
* @param huffCodes2
* @return
*/
private static byte[] zip(byte[] bytes, Map<Byte, String> huffCodes) {
StringBuilder sb = new StringBuilder();
//The byte array to be compressed is processed into a binary string
for(byte b:bytes) {
sb.append(huffCodes.get(b));
}
//Define length
int len;
if(sb.length()%8==0) {
len=sb.length()/8;
}else {
len=sb.length()/8+1;
}
//Used to store compressed byte s
byte[] by = new byte[len];
//Record the location of the new byte
int index = 0;
for(int i=0;i<sb.length();i+=8) {
String strByte;
if(i+8>sb.length()) {
strByte = sb.substring(i);
}else {
strByte = sb.substring(i, i+8);
}
byte byt = (byte)Integer.parseInt(strByte, 2);
by[index]=byt;
index++;
}
return by;
}
//Path for temporary storage
static StringBuilder sb = new StringBuilder();
//Huffman code for storage
static Map<Byte, String> huffCodes = new HashMap<>();
/**
* Get Huffman code according to Huffman tree
* @param tree
* @return
*/
private static Map<Byte, String> getCodes(Node tree) {
if(tree==null) {
return null;
}
getCodes(tree.left,"0",sb);
getCodes(tree.right,"1",sb);
return huffCodes;
}
private static void getCodes(Node node, String code, StringBuilder sb) {
StringBuilder sb2 = new StringBuilder(sb);
sb2.append(code);
if(node.data==null) {
getCodes(node.left, "0", sb2);
getCodes(node.right, "1", sb2);
}else {
huffCodes.put(node.data, sb2.toString());
}
}
/**
* Create Huffman tree
* @param nodes
* @return
*/
private static Node createHuffmanTree(List<Node> nodes) {
while(nodes.size()>1) {
//sort
Collections.sort(nodes);
//Take out the two binary trees with the lowest weight
Node left = nodes.get(nodes.size()-1);
Node right = nodes.get(nodes.size()-2);
//Create a new binary tree
Node parent = new Node(null, left.weight+right.weight);
//Set the two binary trees taken out before as the subtree of the newly created binary tree
parent.left=left;
parent.right=right;
//Delete the two binary trees taken out in front
nodes.remove(left);
nodes.remove(right);
//Put the newly created binary tree into the collection
nodes.add(parent);
}
return nodes.get(0);
}
/**
* Convert byte array to node set
* @param bytes
* @return
*/
private static List<Node> getNodes(byte[] bytes) {
List<Node> nodes = new ArrayList<>();
//Store how many times each byte appears.
Map<Byte, Integer> counts = new HashMap<>();
//Count the number of occurrences of each byte
for(byte b:bytes) {
Integer count = counts.get(b);
if(count==null) {
counts.put(b, 1);
}else {
counts.put(b, count+1);
}
}
//Turn each key value pair into a node object
for(Map.Entry<Byte, Integer> entry:counts.entrySet()) {
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
}
6. Binary sort tree
6.1 introduction
It has the following characteristics:
- In a binary sort tree, if the root node has a left subtree, the values of all nodes on the left subtree are less than the values of the root node;
- If the root of all nodes in the subtree has a right value, then the root of all nodes in the subtree has a binary value;
- The left and right subtrees of a binary sort tree are also required to be binary sort trees;
6.2 code implementation
Node:
public class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value=value;
}
/**
* Add node to subtree
* @param node
*/
public void add(Node node) {
if(node==null) {
return;
}
//Judge whether the value of the incoming node is larger or smaller than the value of the root node of the current subtree
//The added node has a smaller value than the current node
if(node.value<this.value) {
//If the left node is empty
if(this.left==null) {
this.left=node;
//If not empty
}else {
this.left.add(node);
}
}else {
if(this.right==null) {
this.right=node;
}else {
this.right.add(node);
}
}
}
/**
* Middle order traversal
* @param node
*/
public void midShow(Node node) {
if(node==null) {
return;
}
midShow(node.left);
System.out.println(node.value);
midShow(node.right);
}
/**
* Find node
* @param value2
*/
public Node search(int value) {
if(this.value==value) {
return this;
}else if(value<this.value) {
if(left==null) {
return null;
}
return left.search(value);
}else{
if(right==null) {
return null;
}
return right.search(value);
}
}
/**
* Search parent node
* @param value
* @return
*/
public Node searchParent(int value) {
if((this.left!=null&&this.left.value==value)||(this.right!=null&&this.right.value==value)) {
return this;
}else {
if(this.value>value&&this.left!=null) {
return this.left.searchParent(value);
}else if(this.value<value&&this.right!=null){
return this.right.searchParent(value);
}
return null;
}
}
}
Binary sort tree:
public class BinarySortTree {
Node root;
/**
* Adding nodes to a binary sort tree
* @param node
*/
public void add(Node node){
//If it's an empty tree
if(root==null) {
root=node;
}else {
root.add(node);
}
}
/**
* Middle order traverses the binary sort tree in the order from small to large
*/
public void midShow() {
if(root!=null) {
root.midShow(root);
}
}
/**
* Node lookup
* @param value
* @return
*/
public Node search(int value) {
if(root==null) {
return null;
}else {
return root.search(value);
}
}
/**
* Delete node
* @param value
*/
public void delete(int value) {
if(root==null) {
return;
}else {
//Find this node
Node target = search(value);
//Without this node
if(target==null) {
return;
}
//Find his parent node
Node parent = searchParent(value);
//The node to be deleted is a leaf node
if(target.left==null&&target.right==null) {
//The node to be deleted is the left child of the parent node
if(parent.left.value==value) {
parent.left=null;
//The node to be deleted is the right child of the parent node
}else {
parent.right=null;
}
//The node to be deleted has two child nodes
}else if(target.left!=null&&target.right!=null) {
//Delete the node with the smallest value in the right subtree and get the value of the node
int min = deleteMin(target.right);
//Replace the value in the target node
target.value=min;
//The node to be deleted has a left or right child node
}else {
//Left child node
if(target.left!=null) {
//The node to be deleted is the left child of the parent node
if(parent.left.value==value) {
parent.left=target.left;
//The node to be deleted is the right child of the parent node
}else {
parent.right=target.left;
}
//Right child node
}else {
//The node to be deleted is the left child of the parent node
if(parent.left.value==value) {
parent.left=target.right;
//The node to be deleted is the right child of the parent node
}else {
parent.right=target.right;
}
}
}
}
}
/**
* Delete the smallest node in a tree
* @param right
* @return
*/
private int deleteMin(Node node) {
Node target = node;
//Recursive left finding
while(target.left!=null) {
target=target.left;
}
//Delete the smallest node
delete(target.value);
return target.value;
}
/**
* Search parent node
* @param value
* @return
*/
public Node searchParent(int value) {
if(root==null) {
return null;
}else {
return root.searchParent(value);
}
}
}
Test:
public class TestBinarySortTree {
public static void main(String[] args) {
int[] arr = new int[] {7,3,10,12,5,1,9};
//Create a binary sort tree
BinarySortTree bst = new BinarySortTree();
//Cyclic addition
for(int i:arr) {
bst.add(new Node(i));
}
//View values in the tree
bst.midShow();
System.out.println("-----");
//lookup
// Node node = bst.search(10);
// System.out.println(node.value);
//
// Node node2 = bst.search(20);
// System.out.println(node2);
// //Test find parent node
// Node p1 = bst.searchParent(12);
// System.out.println(p1.value);
// System.out.println("-----");
//Delete leaf node
// bst.delete(5);
// bst.midShow();
// System.out.println("===");
//Delete a node that has only one child node
// bst.delete(3);
// bst.midShow();
//Delete a node with two child nodes
bst.delete(3);
System.out.println("----");
bst.midShow();
}
}
7. AVL tree (balanced binary tree)
7.1 introduction
Balanced Binary Tree, also known as AVL tree (different from AVL algorithm), has the following properties: it is an empty tree or the absolute value of the height difference between its left and right subtrees does not exceed 1, and both the left and right subtrees are a Balanced Binary Tree. This scheme solves the problem that the binary search tree degenerates into a linked list, and maintains the time complexity of insertion, search and deletion at O(logN) in the best and worst cases. However, frequent rotation will sacrifice the time of O(logN) for insertion and deletion, but it is much more stable in time than binary search tree.

7.2 implementation of rotation code
public class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value=value;
}
/**
* Returns the height of the current node
* @return
*/
public int height() {
return Math.max(left==null?0:left.height(), right==null?0:right.height())+1;
}
/**
* Gets the height of the left subtree
* @return
*/
public int leftHeight() {
if(left==null) {
return 0;
}
return left.height();
}
/**
* Gets the height of the right subtree
* @return
*/
public int rightHeight() {
if(right==null) {
return 0;
}
return right.height();
}
/**
* Add node to subtree
* @param node
*/
public void add(Node node) {
if(node==null) {
return;
}
//Judge whether the value of the incoming node is larger or smaller than the value of the root node of the current subtree
//The added node has a smaller value than the current node
if(node.value<this.value) {
//If the left node is empty
if(this.left==null) {
this.left=node;
//If not empty
}else {
this.left.add(node);
}
}else {
if(this.right==null) {
this.right=node;
}else {
this.right.add(node);
}
}
//Query balance
//Rotate right
if(leftHeight()-rightHeight()>=2) {
//Double rotation
if(left!=null&&left.leftHeight()<left.rightHeight()) {
//Rotate left first
left.leftRotate();
//Rotate right again
rightRotate();
//Single rotation
}else {
rightRotate();
}
}
//Left rotation
if(leftHeight()-rightHeight()<=-2) {
//Double rotation
if(right!=null&&right.rightHeight()<right.leftHeight()) {
right.rightRotate();
leftRotate();
//Single rotation
}else {
leftRotate();
}
}
}
/**
* Left rotation
*/
private void leftRotate() {
Node newLeft = new Node(value);
newLeft.left=left;
newLeft.right=right.left;
value=right.value;
right=right.right;
left=newLeft;
}
/**
* Right rotation
*/
private void rightRotate() {
//Create a new node with a value equal to the value of the current node
Node newRight = new Node(value);
//Set the right subtree of the new node to the right subtree of the current node
newRight.right=right;
//Set the left subtree of the new node as the right subtree of the left subtree of the current node
newRight.left=left.right;
//Replace the value of the current node with the value of the left child node
value=left.value;
//Set the left subtree of the current node as the left subtree of the left subtree
left=left.left;
//Set the right subtree of the current node as the new node
right=newRight;
}
/**
* Middle order traversal
* @param node
*/
public void midShow(Node node) {
if(node==null) {
return;
}
midShow(node.left);
System.out.println(node.value);
midShow(node.right);
}
/**
* Find node
* @param value2
*/
public Node search(int value) {
if(this.value==value) {
return this;
}else if(value<this.value) {
if(left==null) {
return null;
}
return left.search(value);
}else{
if(right==null) {
return null;
}
return right.search(value);
}
}
/**
* Search parent node
* @param value
* @return
*/
public Node searchParent(int value) {
if((this.left!=null&&this.left.value==value)||(this.right!=null&&this.right.value==value)) {
return this;
}else {
if(this.value>value&&this.left!=null) {
return this.left.searchParent(value);
}else if(this.value<value&&this.right!=null){
return this.right.searchParent(value);
}
return null;
}
}
}
balanced binary tree
public class BinarySortTree {
Node root;
/**
* Adding nodes to a binary sort tree
* @param node
*/
public void add(Node node){
//If it's an empty tree
if(root==null) {
root=node;
}else {
root.add(node);
}
}
/**
* Middle order traverses the binary sort tree in the order from small to large
*/
public void midShow() {
if(root!=null) {
root.midShow(root);
}
}
/**
* Node lookup
* @param value
* @return
*/
public Node search(int value) {
if(root==null) {
return null;
}else {
return root.search(value);
}
}
/**
* Delete node
* @param value
*/
public void delete(int value) {
if(root==null) {
return;
}else {
//Find this node
Node target = search(value);
//Without this node
if(target==null) {
return;
}
//Find his parent node
Node parent = searchParent(value);
//The node to be deleted is a leaf node
if(target.left==null&&target.right==null) {
//The node to be deleted is the left child of the parent node
if(parent.left.value==value) {
parent.left=null;
//The node to be deleted is the right child of the parent node
}else {
parent.right=null;
}
//The node to be deleted has two child nodes
}else if(target.left!=null&&target.right!=null) {
//Delete the node with the smallest value in the right subtree and get the value of the node
int min = deleteMin(target.right);
//Replace the value in the target node
target.value=min;
//The node to be deleted has a left or right child node
}else {
//Left child node
if(target.left!=null) {
//The node to be deleted is the left child of the parent node
if(parent.left.value==value) {
parent.left=target.left;
//The node to be deleted is the right child of the parent node
}else {
parent.right=target.left;
}
//Right child node
}else {
//The node to be deleted is the left child of the parent node
if(parent.left.value==value) {
parent.left=target.right;
//The node to be deleted is the right child of the parent node
}else {
parent.right=target.right;
}
}
}
}
}
/**
* Delete the smallest node in a tree
* @param right
* @return
*/
private int deleteMin(Node node) {
Node target = node;
//Recursive left finding
while(target.left!=null) {
target=target.left;
}
//Delete the smallest node
delete(target.value);
return target.value;
}
/**
* Search parent node
* @param value
* @return
*/
public Node searchParent(int value) {
if(root==null) {
return null;
}else {
return root.searchParent(value);
}
}
}
Test:
public class TestBinarySortTree {
public static void main(String[] args) {
// int[] arr = new int[] {8,9,6,7,5,4};
int[] arr = new int[] {8,9,5,4,6,7};
//Create a binary sort tree
BinarySortTree bst = new BinarySortTree();
//Cyclic addition
for(int i:arr) {
bst.add(new Node(i));
}
//View height
System.out.println(bst.root.height());
//
System.out.println(bst.root.value);
}
}
8. Multiple lookup tree
8.1 computer storage
Memory storage is much faster than disk storage.
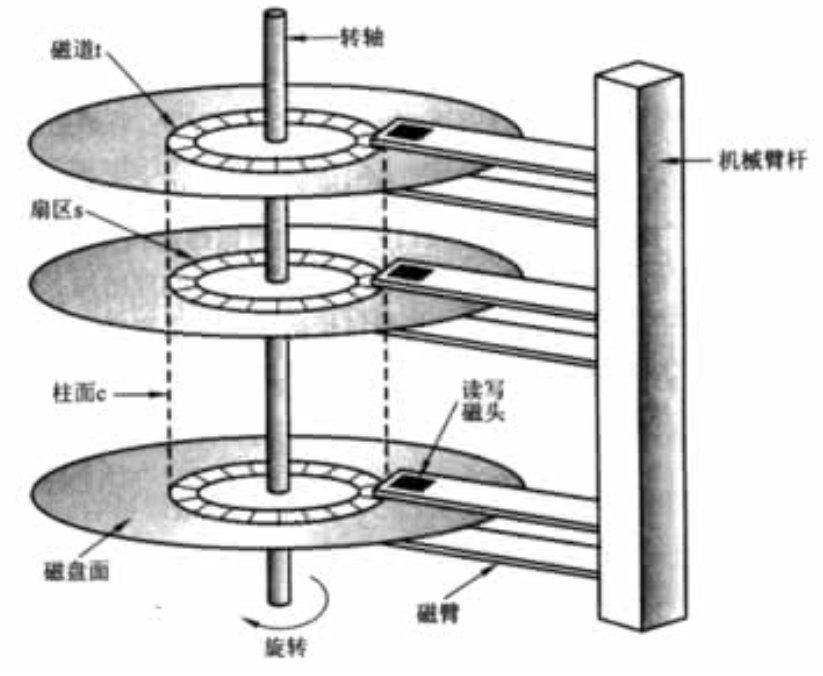
There are circles of tracks on the disk. We use the magnetic arm to read and write. This is obviously much slower. Moreover, because the disk reading is relatively slow, the disk will reduce the IO operation of the disk. It will pre read part of the data into the memory in advance. This part of the data is not read on demand, but read a certain length of data. Maybe this part of the data can be used immediately or not. The length of the preview is generally an integral multiple of the page.
Then look again. If you read a binary tree, you will first read part of it into memory, but due to the limited memory, you will read part of the data into disk. A node of a binary tree is a page. In this way, each read IO operation actually accesses only one node.
In this way, it is better to use multi-channel search tree.
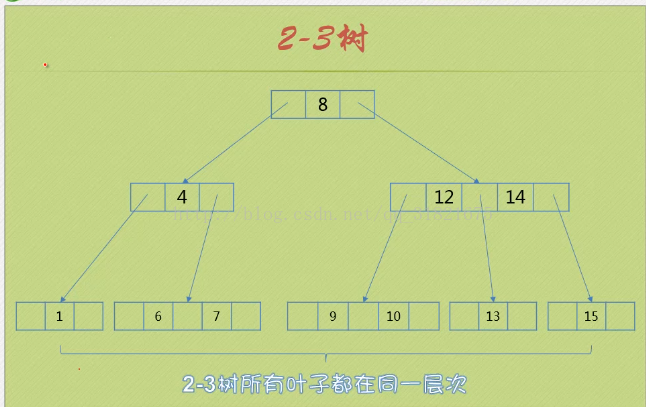
8.2-3 tree
2-3 tree is the simplest B-tree (or tree) structure. Each non leaf node has two or three children, and all leaves are on the same layer.
2-3 tree lookup element 5:
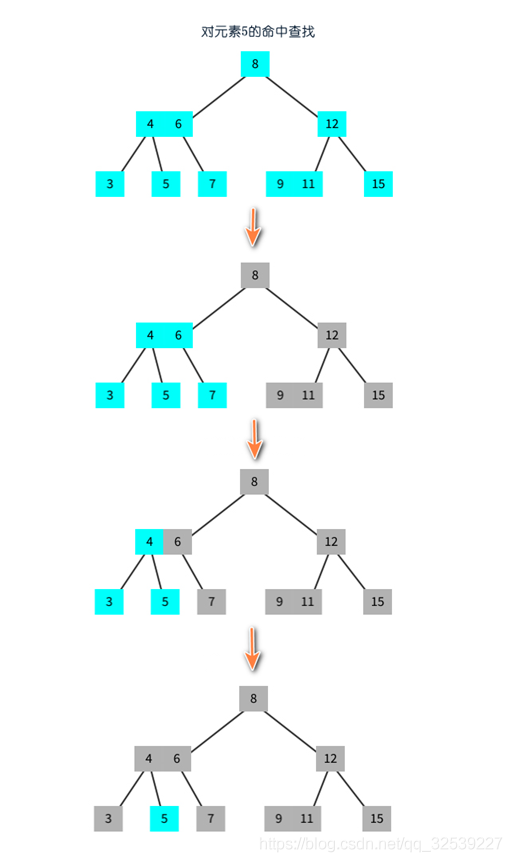
2-3 where data is added to an element in the tree:
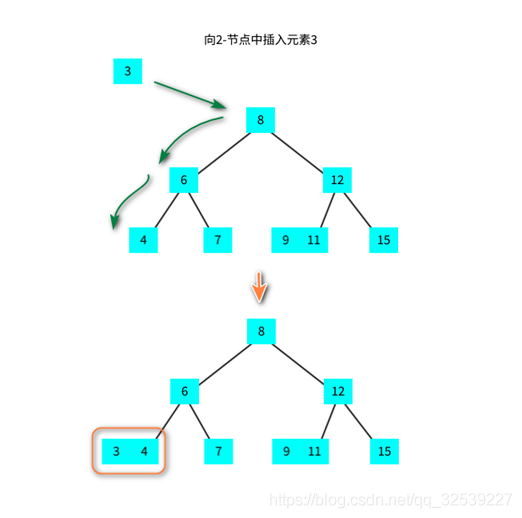
2-3 add data to the two elements of the tree:
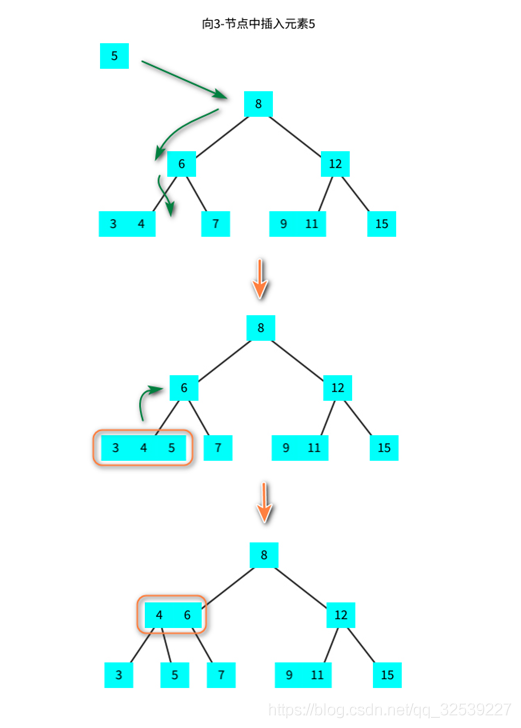
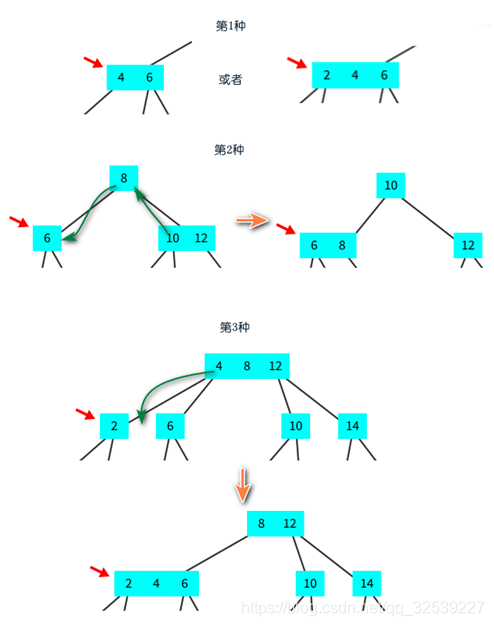
2-3 another case of adding elements to a tree:
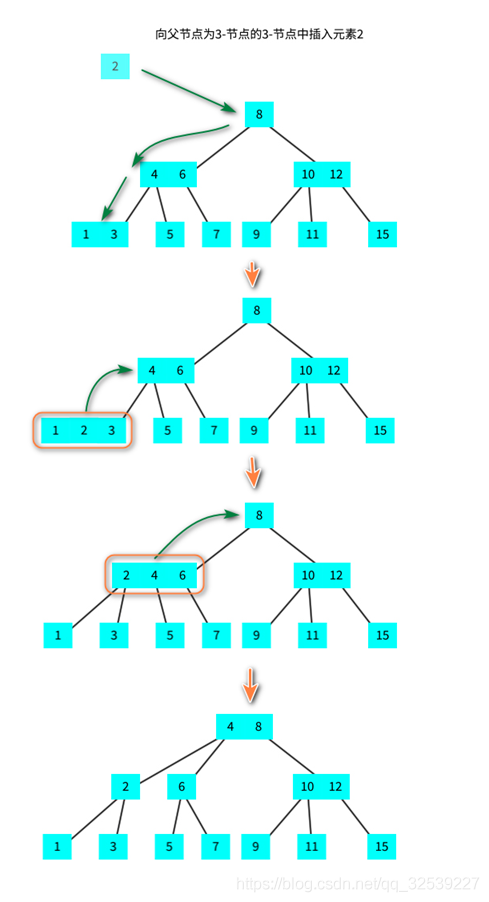
2-3 delete elements from tree:
8.3 B-tree and B + tree
B tree is basically similar to two or three trees.
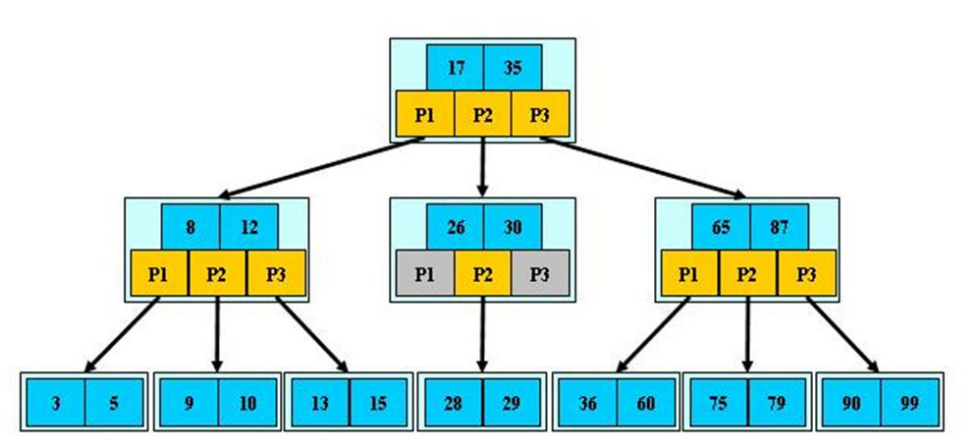
8, Hash table (hash table)
1. Introduction
It is a data structure accessed directly according to the key value. That is, it accesses records by mapping key values to a location in the table to speed up the search. This mapping function is called hash function, and the array storing records is called hash table.
2. Code implementation
Student information
public class StuInfo {
private int age;
private int count;
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
public int getCount() {
return count;
}
public void setCount(int count) {
this.count = count;
}
/**
* Hash function
*/
public int hashCode() {
return age;
}
public StuInfo(int age, int count) {
super();
this.age = age;
this.count = count;
}
public StuInfo(int age) {
super();
this.age = age;
}
@Override
public String toString() {
return "StuInfo [age=" + age + ", count=" + count + "]";
}
}
Hash table:
public class HashTable {
private StuInfo[] data = new StuInfo[100];
/**
* Add an element to the hash table
* @param stuInfo
*/
public void put(StuInfo stuInfo) {
//Call the hash function to get the storage location
int index = stuInfo.hashCode();
//Add element
data[index]=stuInfo;
}
public StuInfo get(StuInfo stuInfo) {
return data[stuInfo.hashCode()];
}
@Override
public String toString() {
return "HashTable [data=" + Arrays.toString(data) + "]";
}
}
Test:
public class TestHashTable {
public static void main(String[] args) {
StuInfo s1 = new StuInfo(16, 3);
StuInfo s2 = new StuInfo(17, 11);
StuInfo s3 = new StuInfo(18, 23);
StuInfo s4 = new StuInfo(19, 24);
StuInfo s5 = new StuInfo(20, 9);
HashTable ht = new HashTable();
ht.put(s1);
ht.put(s2);
ht.put(s3);
ht.put(s4);
ht.put(s5);
System.out.println(ht);
//Target data you want to obtain
StuInfo target = new StuInfo(18);
StuInfo info = ht.get(target);
System.out.println(info);
}
}
3. Address conflict problem
3.1 open address method
After a hash conflict occurs, find the next free unit in a certain order and put the conflicting elements into.
3.1.1 linear exploration method
Start from the conflicting cell and check whether the next cell is empty in turn. If the last cell is still empty, judge from the beginning of the table in turn. This is done until an idle unit is encountered or all units have been explored.
3.2.2 square probe method
Add 12,22,32,..., n2 from the conflicting unit until an idle unit is encountered.
3.2 chain address method
The elements with the same hash value form a linked list, and the head is placed in the hash table. Generally, if the length of the linked list exceeds 8, it will become a red black tree, and if the length is less than 6, it will become a linked list.
3.3 rehashifa
Construct multiple different hash functions at the same time, Hi = RHi(key) i= 1,2,3... k; When H1 = RH1(key) conflicts, H2 = RH2(key) is used for calculation until the conflict no longer occurs. This method is not easy to produce aggregation, but increases the calculation time.
9, Figure
1. Introduction
When we need to represent many to many relationships, the previous trees and linked lists are not suitable. Graphs are used at this time.
A graph is a data structure in which a node can have zero or more adjacent elements. The connection between two nodes is called an edge. Nodes can also be called vertices.
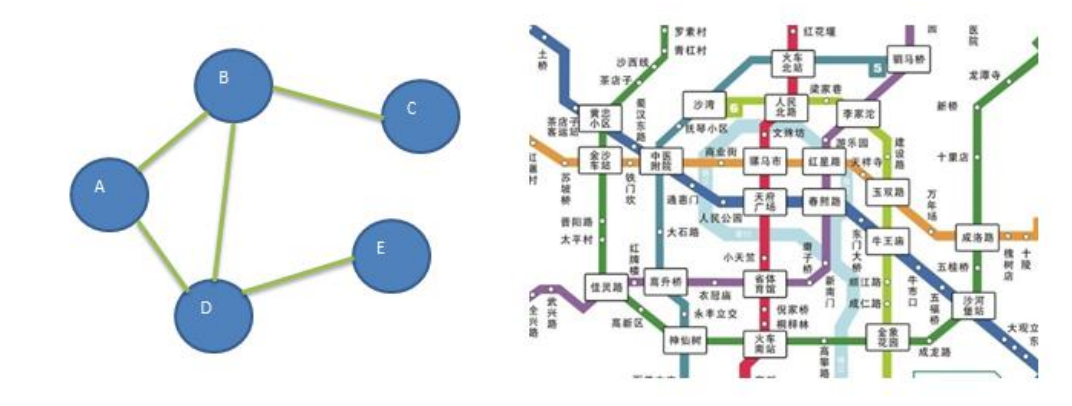
If there is an arrow, it is a directed graph, and if there is no arrow, it is an undirected graph.
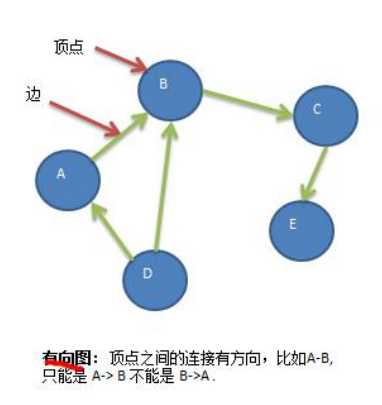
The graph with weights is a weighted graph.
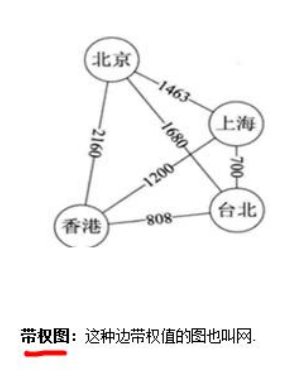
2. Code implementation
public class Vertex {
private String value;
public boolean visited;
public String getValue() {
return value;
}
public void setValue(String value) {
this.value = value;
}
public Vertex(String value) {
super();
this.value = value;
}
@Override
public String toString() {
return value;
}
}
Figure structure:
public class Graph {
private Vertex[] vertex;
private int currentSize;
public int[][] adjMat;
private MyStack stack = new MyStack();
//Subscript of current traversal
private int currentIndex;
public Graph(int size) {
vertex=new Vertex[size];
adjMat=new int[size][size];
}
/**
* Add a vertex to the graph
* @param v
*/
public void addVertex(Vertex v) {
vertex[currentSize++]=v;
}
public void addEdge(String v1,String v2) {
//Find the subscript of two vertices
int index1=0;
for(int i=0;i<vertex.length;i++) {
if(vertex[i].getValue().equals(v1)) {
index1=i;
break;
}
}
int index2=0;
for(int i=0;i<vertex.length;i++) {
if(vertex[i].getValue().equals(v2)) {
index2=i;
break;
}
}
adjMat[index1][index2]=1;
adjMat[index2][index1]=1;
}
/**
* Depth first search algorithm traversal graph
*/
public void dfs() {
//Mark the 0th vertex as accessed
vertex[0].visited=true;
//Subscript the 0 th vertex.
stack.push(0);
//Print vertex values
System.out.println(vertex[0].getValue());
//ergodic
out:while(!stack.isEmpty()) {
for(int i=currentIndex+1;i<vertex.length;i++) {
//If it is connected to the next traversal element
if(adjMat[currentIndex][i]==1&&vertex[i].visited==false) {
//Push the next element onto the stack
stack.push(i);
vertex[i].visited=true;
System.out.println(vertex[i].getValue());
continue out;
}
}
//Pop up stack top element
stack.pop();
//Modify the current position to the position of the top element of the stack
if(!stack.isEmpty()) {
currentIndex=stack.peek();
}
}
}
}
Test:
public class TestGraph {
public static void main(String[] args) {
Vertex v1 = new Vertex("A");
Vertex v2 = new Vertex("B");
Vertex v3 = new Vertex("C");
Vertex v4 = new Vertex("D");
Vertex v5 = new Vertex("E");
Graph g = new Graph(5);
g.addVertex(v1);
g.addVertex(v2);
g.addVertex(v3);
g.addVertex(v4);
g.addVertex(v5);
//Add edge
g.addEdge("A", "C");
g.addEdge("B", "C");
g.addEdge("A", "B");
g.addEdge("B", "D");
g.addEdge("B", "E");
for(int[] a:g.adjMat) {
System.out.println(Arrays.toString(a));
}
//Depth first traversal
g.dfs();
}
}
10, Sorting algorithm
0. Sorting algorithm classification
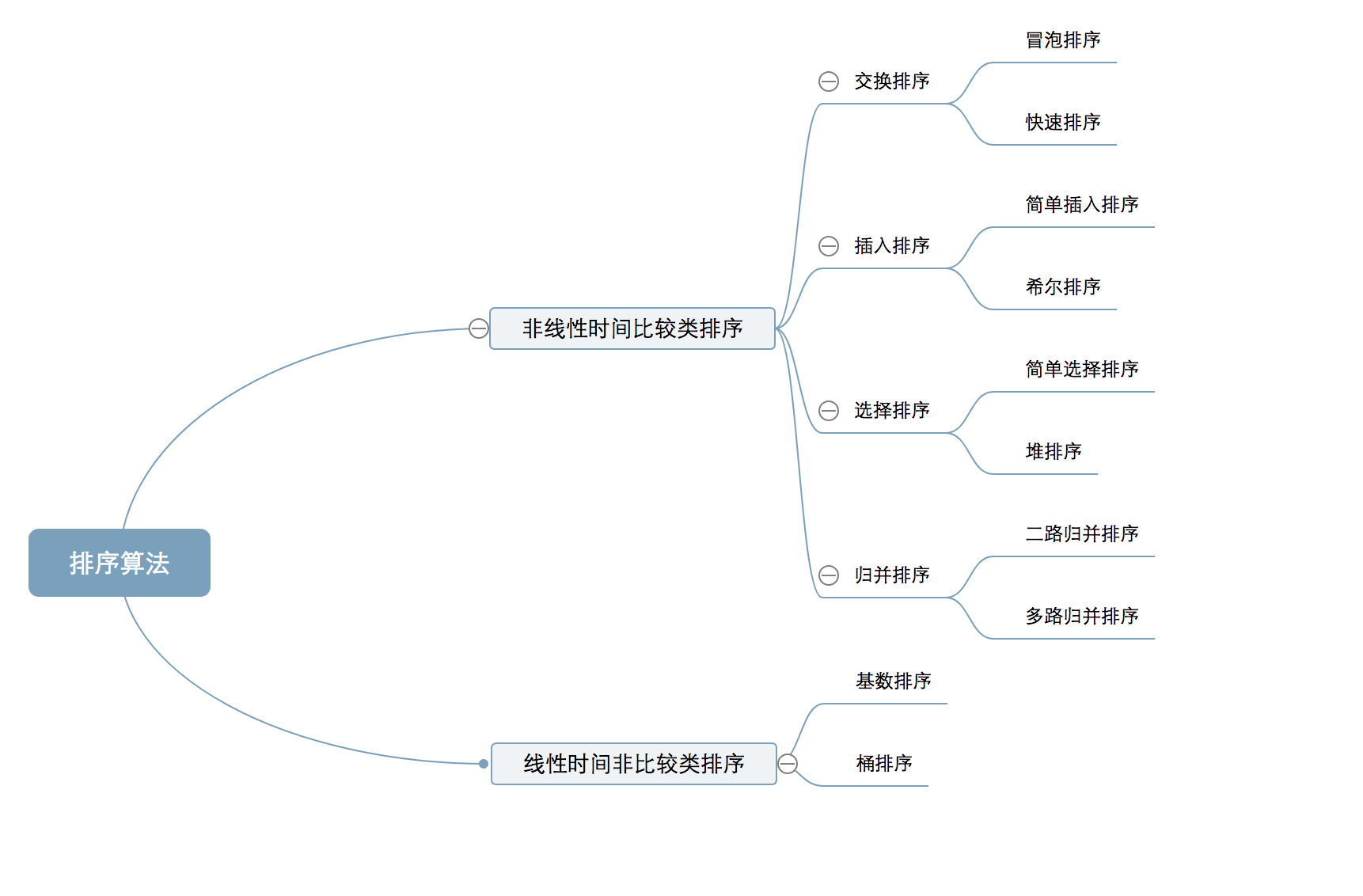
1. Bubble sorting
1.1 schematic diagram
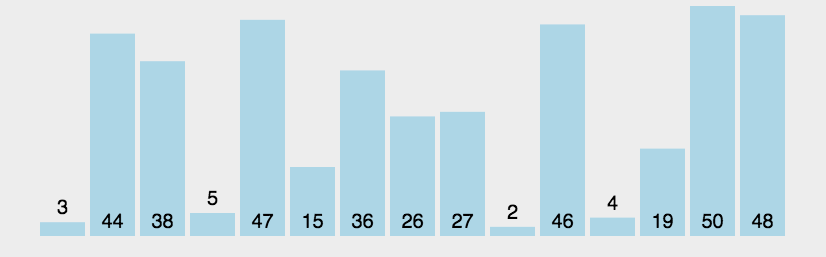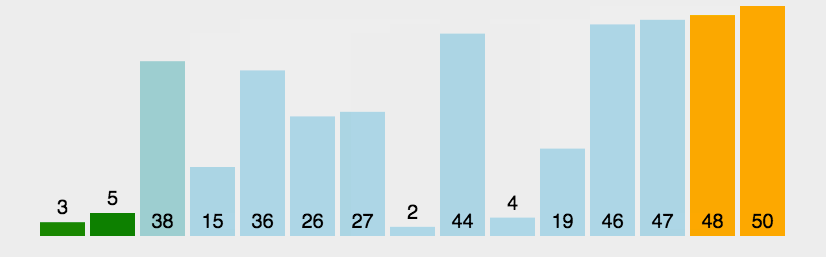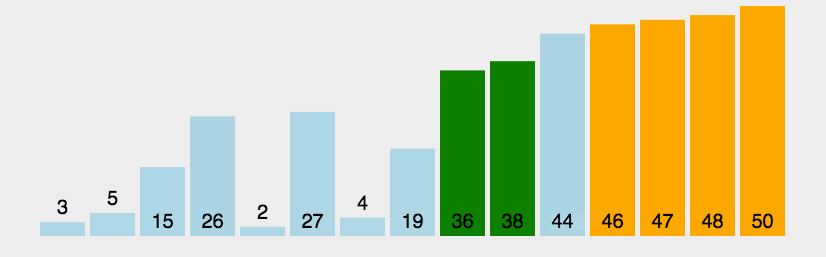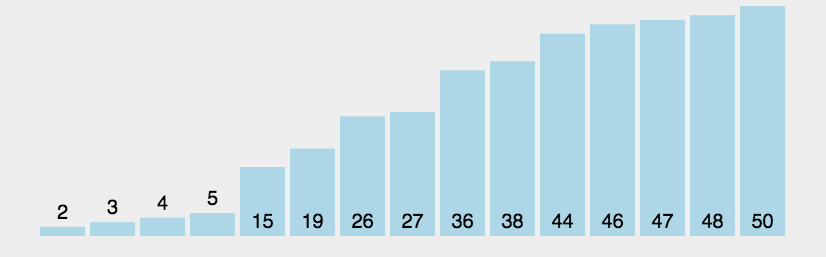
1.2 code implementation
public class BubbleSort {
public static void main(String[] args) {
int[] arr = new int[]{10,6,2,14,5,7,15,4,1,3};
bubbleSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void bubbleSort(int[] arr){
for (int i = 0;i < arr.length;i++){
for (int j = 0;j < arr.length - 1 - i;j++){
if (arr[j] > arr[j+1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
}
2. Selective sorting method
2.1 schematic diagram
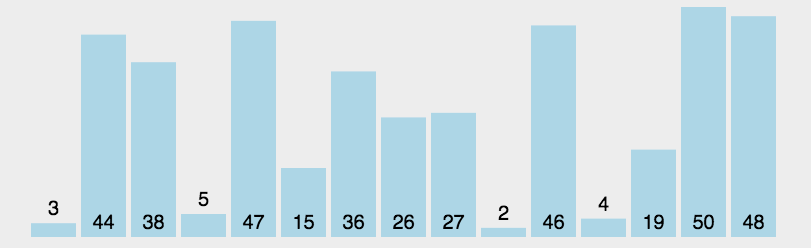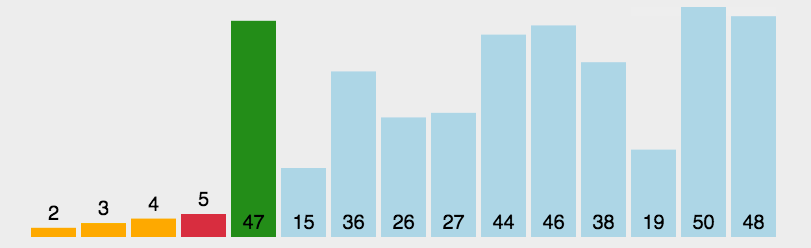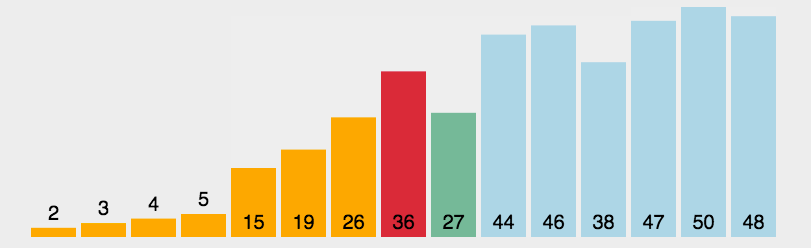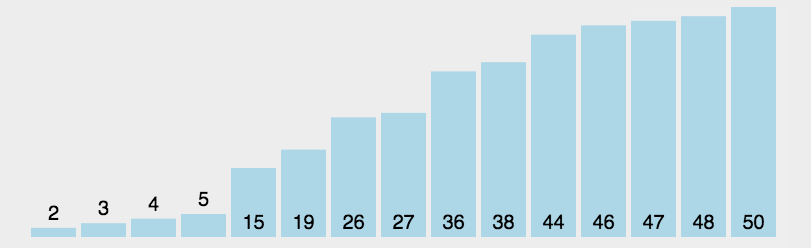
2.2 code implementation
public class SelectSort {
public static void main(String[] args) {
int[] elements = new int[]{10,5,15,2,6,4,14,11,1,101,23};
selectSort(elements);
System.out.println(Arrays.toString(elements));
}
public static void selectSort(int[] ele){
for(int i = 0;i < ele.length;i++){
int minIndex = i;
for (int j = i + 1;j < ele.length;j++){
if (ele[minIndex] > ele[j]){
minIndex = j;
}
}
if (minIndex != i){
int temp = ele[i];
ele[i] = ele[minIndex];
ele[minIndex] = temp;
}
}
}
}
3. Quick sorting method
3.1 schematic diagram
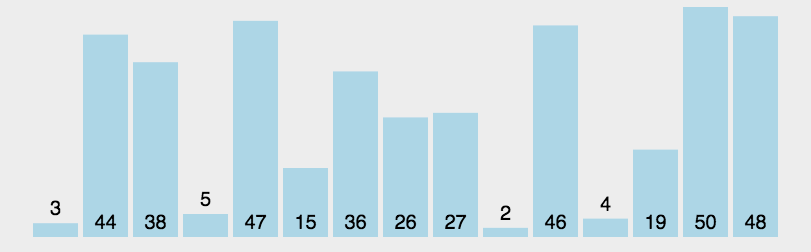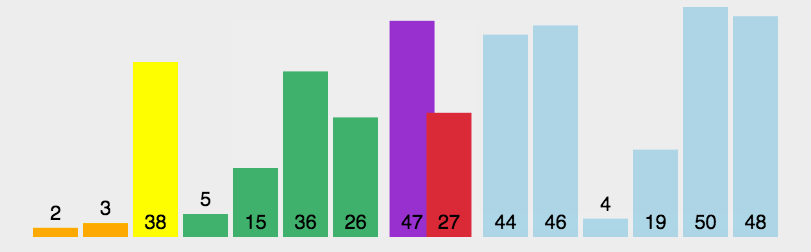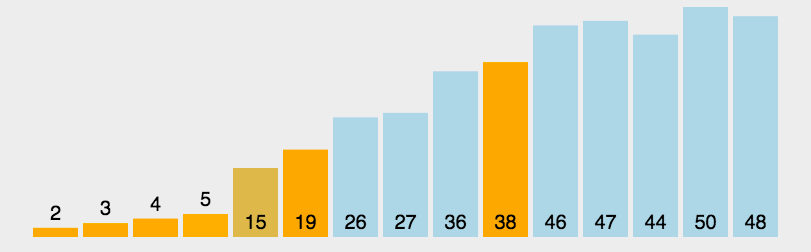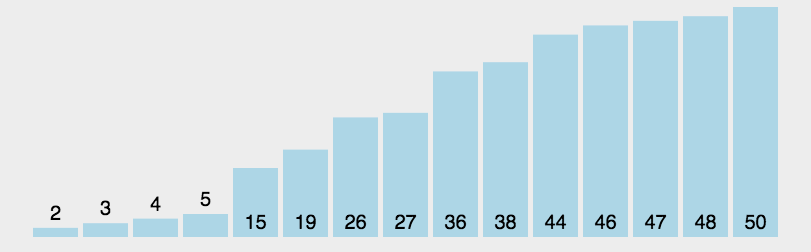
3.2 code implementation
public class QuickSort {
public static void main(String[] args) {
int[] arr = new int[]{10,2,5,16,3,7,17,8,4,25,-11,223,100};
quickSort(arr,0,arr.length-1);
System.out.println(Arrays.toString(arr));
}
public static void quickSort(int[] arr,int start,int end){
if (start < end){
//Define a standard value
int standard = arr[start];
//Define two starting Subscripts
int low = start;
int high = end;
//Cycle
while (low < high){
//When the right value is larger than the standard value, keep moving the high subscript
while(low < high && arr[high] >= standard){
high--;
}
//When it is found that it is smaller than the standard value, change the value directly
arr[low] = arr[high];
while(low < high && arr[low] <= standard){
low++;
}
arr[high] = arr[low];
}
//After the cycle is finished, low = high, then assign a value to arr[low]
arr[low] = standard;
quickSort(arr,start,low);
quickSort(arr,low+1,end);
}
}
}
4. Insert sort
4.1 schematic diagram
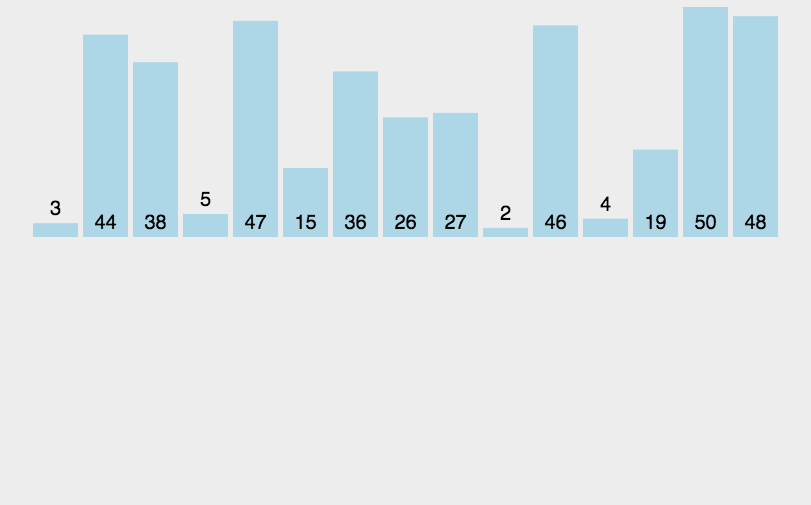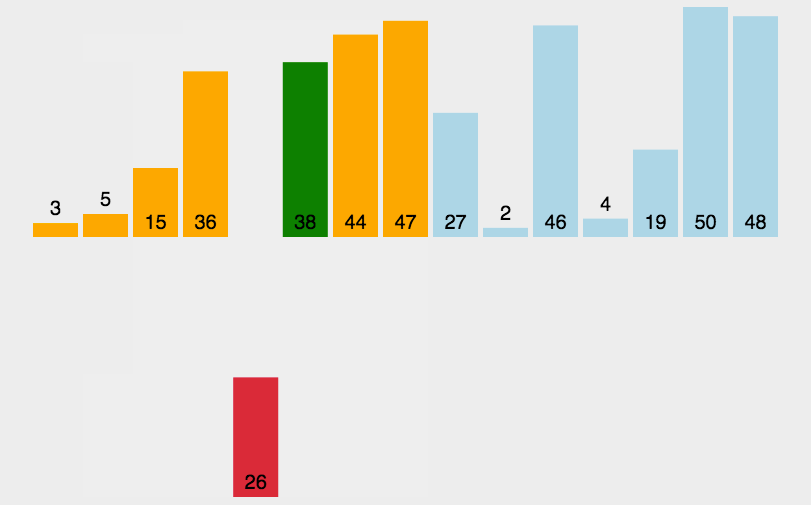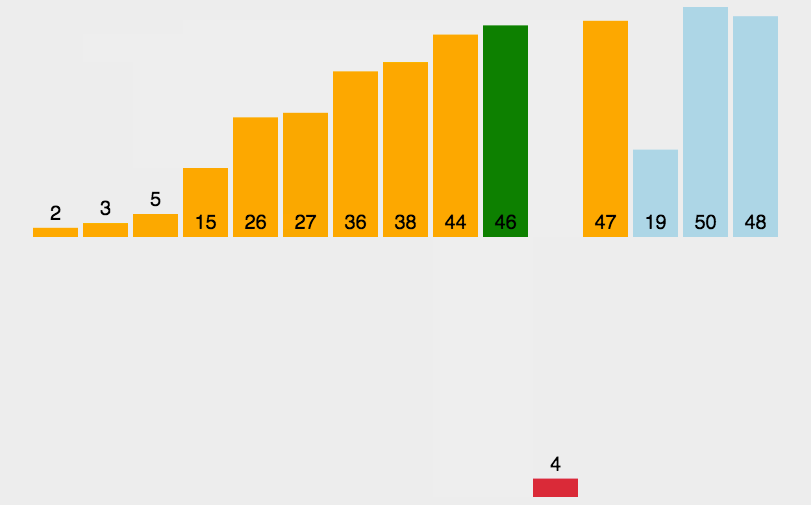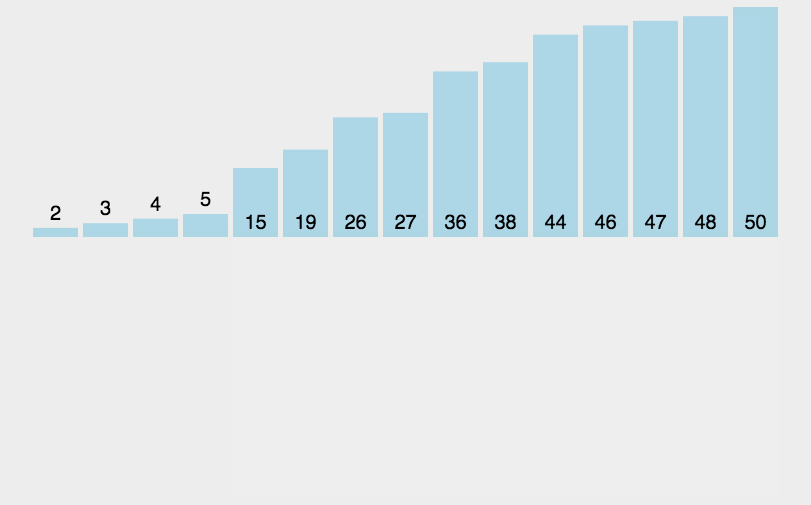
4.2 code implementation
public class InsertSort {
public static void main(String[] args) {
int[] array = new int[]{11,5,2,16,7,3,10,3,1};
insertSort(array);
System.out.println(Arrays.toString(array));
}
/**
* Insert sort logic
* @param array Array to sort
*/
public static void insertSort(int[] array){
//Number of outer ring control cycles
for (int i = 1;i < array.length;i++){
//If this number is smaller than the previous number
if (array[i] < array[i-1]){
//Assign this value to a temporary variable first
int temp = array[i];
//Then assign the subscript of a quadratic cycle
int j;
//Loop forward from the previous position of the current subscript until an element smaller than it is found
for (j = i - 1;j >= 0 && array[j] > temp;j--){
array[j+1] = array[j];
}
array[j+1] = temp;
}
}
}
}
5. Merge sort
5.1 schematic diagram
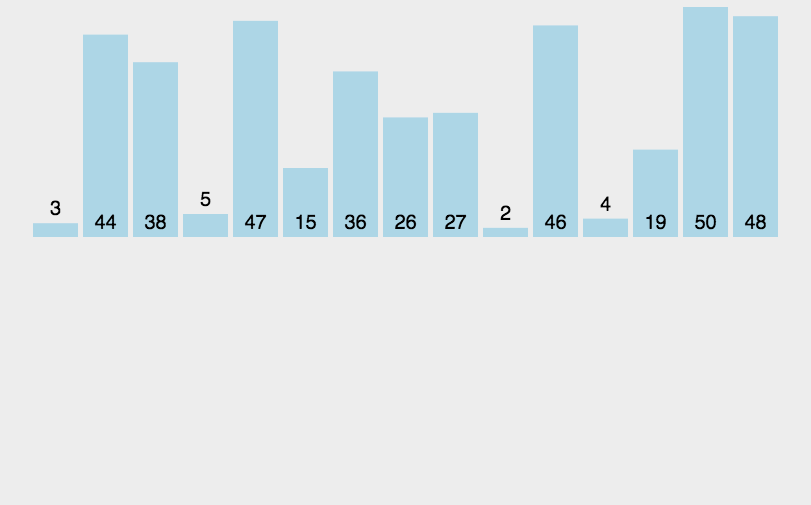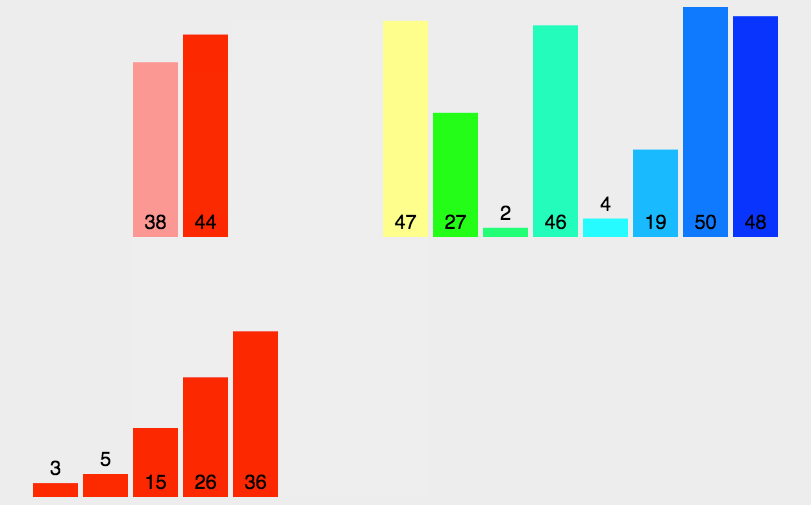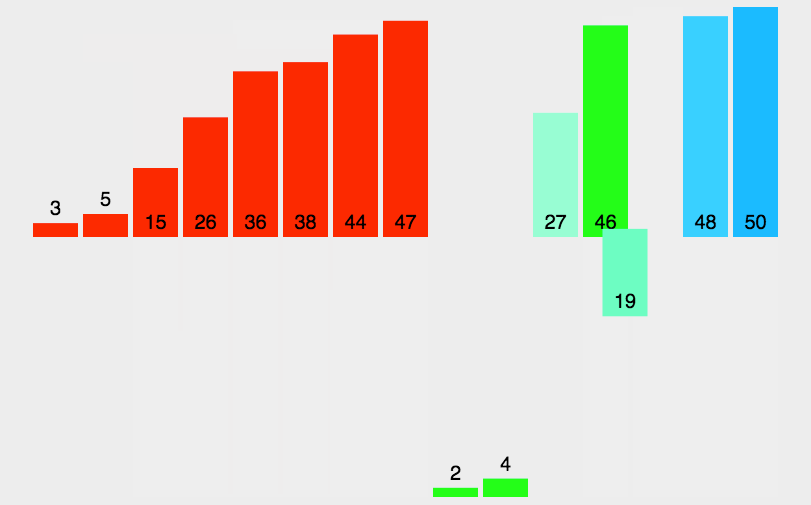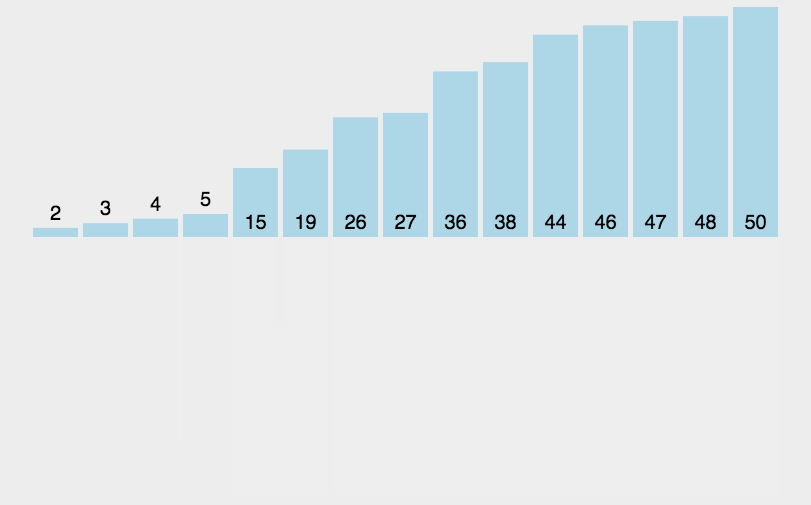
5.2 code implementation
public class MergeSort {
public static void main(String[] args) {
int[] arr = new int[]{11,5,8,18,2,5,3,9,6,13,7};
mergeSort(arr,0,arr.length-1);
System.out.println(Arrays.toString(arr));
}
/**
* Merge sort
* @param arr
* @param low
* @param high
*/
public static void mergeSort(int[] arr,int low,int high){
int middle = (low + high)/2;
if (low < high){
mergeSort(arr,low,middle);
mergeSort(arr,middle+1,high);
merge(arr,low,middle,high);
}
}
/**
* Merging logic
* @param arr
* @param low
* @param middle
* @param high
*/
public static void merge(int[] arr,int low,int middle,int high){
//Create a temporary array for placing elements
int[] temp = new int[high-low+1];
//Record the initial value of the first array
int i = low;
//Record the initial value of the second array
int j = middle + 1;
//You also need a subscript to record the location of the new array
int index = 0;
//Loop. If both arrays are not finished, continue the loop
while(i <= middle && j <= high){
if (arr[i] <= arr[j]){
temp[index] = arr[i];
i++;
}else{
temp[index] = arr[j];
j++;
}
index++;
}
//When a cycle is finished, follow this cycle. If it is not finished, continue to add value
while(i <= middle){
temp[index] = arr[i];
i++;
index++;
}
while(j <= high){
temp[index] = arr[j];
j++;
index++;
}
//Move the value in temp into the original array
for (int k = 0;k < temp.length;k++){
arr[k+low] = temp[k];
}
}
}
6. Hill sort
6.1 schematic diagram
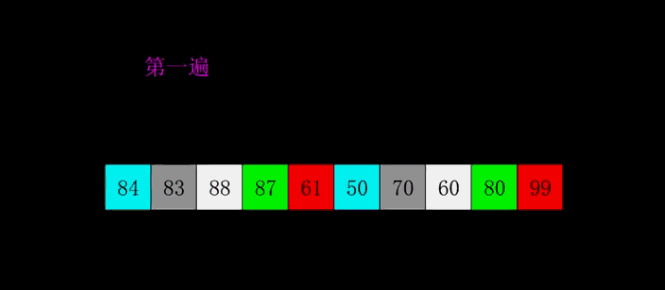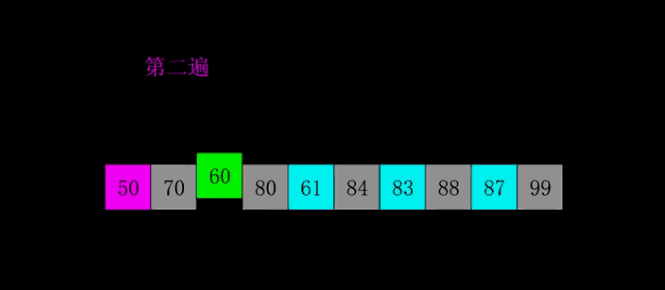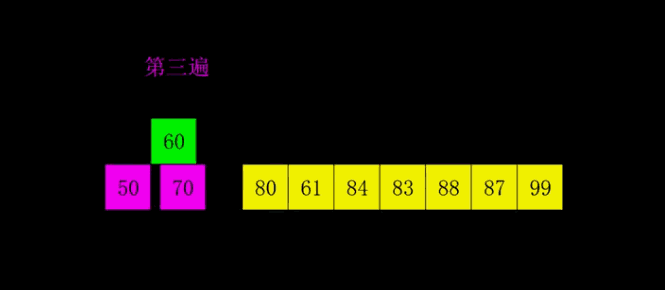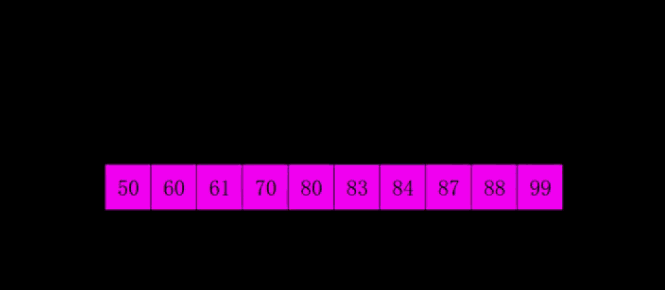
6.2 code implementation
public class ShellSort {
public static void main(String[] args) {
int[] arr = new int[] {11,6,5,16,2,9,1,25,5,0};
System.out.println(Arrays.toString(arr));
shellSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void shellSort(int[] arr) {
int k = 1;
// Traverse all steps
for (int d = arr.length / 2; d > 0; d /= 2) {
// Traverse all existing elements
for (int i = d; i < arr.length; i++) {
// Traverse all elements in this group
for (int j = i - d; j >= 0; j -= d) {
// If the current element is larger than the element after adding the step size
if (arr[j] > arr[j + d]) {
int temp = arr[j];
arr[j] = arr[j + d];
arr[j + d] = temp;
}
}
}
System.out.println("The first" + k + "Secondary sorting result:" + Arrays.toString(arr));
k++;
}
}
}
7. Cardinality sort
7.1 schematic diagram

7.2 code implementation
public class RadixSort {
public static void main(String[] args) {
int[] arr = new int[] {23,6,189,45,9,287,56,1,798,34,65,652,5};
radixSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void radixSort(int[] arr){
//The largest number stored in the array
int max = Integer.MIN_VALUE;
for (int i = 0;i < arr.length;i++){
if (arr[i] > max){
max = arr[i];
}
}
//Look at the maximum number
int maxLength = (max+"").length();
//Create an array of these numbers
int[][] temp = new int[10][arr.length];
//You also need an array to store how many cells there are in each cell
int[] counts = new int[10];
//The outermost loop determines how many times to cycle
for (int i = 0,n = 1;i < maxLength;i++,n*=10){
//The inner loop traverses each number
for (int j = 0;j < arr.length;j++){
//Calculate remainder
int ys = arr[j]/n % 10;
temp[ys][counts[ys]] = arr[j];
counts[ys]++;
}
//Array subscript
int index = 0;
//Take out the elements and traverse each column
for (int k = 0;k < counts.length;k++){
//If this column is not 0
if (counts[k] != 0){
//So let's see how many elements there are. How many times
for (int l = 0;l < counts[k];l++){
arr[index] = temp[k][l];
index++;
}
counts[k] = 0;
}
}
}
}
}
8. Bucket sorting
8.1 schematic diagram

8.2 code implementation
public class BottleSort {
public static void main(String[] args) {
int[] x = {20,12,44,145,111,22,102,122,3,14,292,15,8};
int[] sorted = bucketSort(x, 500);
for (int i = 0; i < sorted.length; i++)
{
if (sorted[i] > 0)
System.out.println(sorted[i]);
}
}
public static int[] bucketSort(int[] nums, int maxNum){
int[] sorted = new int[maxNum+1];
for(int i=0; i<nums.length; i++){
sorted[nums[i]] = nums[i];//Put the data in the corresponding index position
}
return sorted;
}
}
9. Heap sort
9.1 schematic diagram

9.2 code implementation
public class HeapSort {
public static void main(String[] args) {
int[] arr = new int[] {9,6,8,7,0,1,10,4,2};
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void heapSort(int[] arr) {
//The start position is the last non leaf node, that is, the parent node of the last node
int start = (arr.length-1)/2;
//Adjust to large top pile
for(int i=start;i>=0;i--) {
maxHeap(arr, arr.length, i);
}
//First swap the position of the 0th in the array and the last number in the heap, and then treat the previous as a large top heap
for(int i=arr.length-1;i>0;i--) {
int temp = arr[0];
arr[0]=arr[i];
arr[i]=temp;
maxHeap(arr, i, 0);
}
}
public static void maxHeap(int[] arr,int size,int index) {
//Left child node
int leftNode = 2*index+1;
//Right child node
int rightNode = 2*index+2;
int max = index;
//Compare with the two child nodes to find the largest node
if(leftNode<size&&arr[leftNode]>arr[max]) {
max=leftNode;
}
if(rightNode<size&&arr[rightNode]>arr[max]) {
max=rightNode;
}
//change of position
if(max!=index) {
int temp=arr[index];
arr[index]=arr[max];
arr[max]=temp;
//After switching positions, the previously arranged heap may be destroyed. Therefore, the previously arranged heap needs to be readjusted
maxHeap(arr, size, max);
}
}
}