1: Binary search

Binary search algorithm (non recursive) Introduction

(1) Previously, we talked about the binary search algorithm, which uses the recursive method. Next, we will explain the non recursive method of the binary search algorithm

(2) The binary search method is only suitable for searching from an ordered sequence of numbers (such as numbers and letters), sorting the sequence and then searching

(3) The running time of binary search method is logarithmic time O(log2n), that is, only log2n steps are required to find the required target location at most. Assuming that 30 targets are found from the queue (100 numbers, i.e. n=100) of [0 ~ 99], the number of search steps is log2100, that is, 7 times at most (2 ^ 6 < 100 < 2 ^ 7)

Binary search algorithm (non recursive) code implementation

Requirements: the array {1,3,8,10,11,67100} is programmed to realize binary search, which is required to be completed by non recursive method

package binarySearchNoRecur;

/**
 * Binary search non recursive
 */
public class BinarySearchNoRecur {
    public static void main(String[] args) {
        //test
        int [] arr ={1,3,8,10,11,67,100};
        int index = binarySearch(arr,-8);
        System.out.println("index="+index);
    }

    /**
     * Non recursive implementation of binary search
     * @param arr Array to find
     * @param target Number of to find
     * @return The subscript - 1 of the number found indicates that it is not found
     */
    public static int binarySearch(int[] arr ,int target){

        int left = 0; //start
        int right = arr.length -1; //end
        while(left <= right){ //Description continue to find
            int mid = (left + right) / 2;
            if (arr[mid] == target){
                return mid;
            }else if ( arr[mid] > target){
                right = mid -1; //You need to look to the left
            }else {
                left = mid + 1; //You need to look to the right
            }
        }
        return -1;
    }
}

2: Divide and conquer algorithm

Introduction to divide and conquer algorithm

(1) Divide and conquer is a very important algorithm The literal explanation is "divide and rule", which is to divide a complex problem into two or more identical or similar subproblems, and then divide the subproblem into smaller subproblems Until the end, the subproblem can be solved simply and directly, and the solution of the original problem is the combination of the solutions of the subproblem This technique is the basis of many efficient algorithms Incoming sorting algorithm (fast sorting, merging sorting), Fourier transform

(2) Divide and conquer algorithm can solve some classical problems

Binary search

Large integer multiplication

Chess and card coverage

Merge sort

Quick sort

Linear time selection

Closest point pair problem

Cycling schedule

Hanoi

Basic steps of divide and conquer algorithm

Divide and conquer has three steps on each layer of recursion:

(1) Decomposition: decompose the original problem into several small-scale, independent subproblems with the same form as the original problem

(2) Solution: if the subproblem is small and easy to be solved, solve it directly, otherwise solve each subproblem recursively

(3) Merge: merge the solutions of each sub problem into the solutions of the original problem

The divide and conquer algorithm design mode is as follows:

Where | P | represents the scale of problem p; n0 is a threshold, which means that when the scale of problem P does not exceed n0, the problem is easy to be solved directly, and there is no need to continue decomposition. ADHOC(P) is the basic sub algorithm of the divide and conquer method, which is used to directly solve small-scale problem P. Therefore, when the scale of P does not exceed n0, it is directly solved by the algorithm ADHOC(P). The algorithm MERGE(y1,y2.yk) is the merging sub algorithm in the divide and conquer method, which is used to solve the sub problems P1 and P2 of P The corresponding solutions Y1, Y2, YK is merged into the solution of P.
 

Best practice of divide and conquer algorithm - Hanoi Tower

>Legend of the tower of Hanoi
Hanoi Tower: the problem of Hanoi Tower (also known as Hanoi Tower) is an educational toy derived from an ancient Indian legend. When Brahma created the world, he made three diamond pillars. On one pillar, 64 gold discs were stacked in order of size from bottom to top. Brahma ordered Brahman to rearrange the disk on another column in order of size from below. It is also stipulated that the disc cannot be enlarged on the small disc, and only one disc can be moved between the three columns at a time.
If every second, how long does it take? It takes more than 584.554 billion years to remove these gold pieces, and the life expectancy of the solar system is said to be tens of billions of years. After 584.554 billion years, all life on earth, including Vatican pagodas and temples, has long been extinguished.

Analysis of Hanoi tower game

(1) If there is a disk, a - > C

If we have n > = 2, we can always regard it as two disks 1 Bottom disk, 2 top disk

(1) First put the top plate a - > B

(2) Put the lowest disk a - > C

(3) Remove all trays of Tower B from B - > C

Code implementation:

package dac;

/**
 * Divide and conquer algorithm -- Hanoi Tower problem
 */
public class hannuota {
    public static void main(String[] args) {
        hanoiTower(5,'A','B','C');

    }

    //Moving method of Hanoi Tower
    //Using divide and conquer algorithm
    public static void hanoiTower(int num, char a, char b, char c){
        //If there is only one disk
        if (num == 1){
            System.out.println("1st disk from"+ a + "->" + c);
        }else {
            //If we have n > = 2, we can always regard it as two disks 1 The bottom disk 2 All disks above
            //1. First put all the uppermost disks a - > b, and c will be used during the movement
            hanoiTower(num -1, a, c, b);
            //2. Turn the bottom plate A-C
            System.out.println("The first" + num + "Disk from" + a + "->" +c );
            //3. Move all trays of Tower B from B - > C to a
            hanoiTower(num -1, b, a, c);
        }
    }
}

III dynamic programming algorithm

Application scenario - Knapsack Problem

Backpack problem. There is a backpack with a capacity of 4 pounds. There are the following items

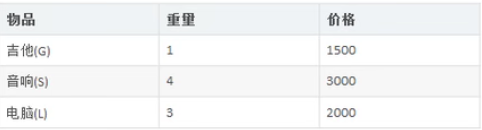
(1) The goal to be achieved is to maximize the total value of the backpack and not exceed the weight

(2) The items required to be loaded cannot be repeated

Introduction to dynamic programming algorithm

(1) The core idea of dynamic programming algorithm is to divide large problems into small problems to solve, so as to obtain the optimal solution step by step
(2) Dynamic programming algorithm is similar to divide and conquer algorithm. Its basic idea is to decompose the problem to be solved into several subproblems. First solve the subproblems, and then get the solution of the original problem from the solutions of these subproblems.
(3) Different from the divide and conquer method, the sub problems obtained by decomposition are often not independent of each other. (that is, the solution of the next sub stage is based on the solution of the previous sub stage for further solution)
(4) Dynamic programming can be advanced step by step by filling in tables to obtain the optimal solution
 

Dynamic specification algorithm best practice - Knapsack Problem

Train of thought analysis and illustration

(3) Knapsack problem only refers to a given capacity knapsack, several items with certain value and weight, how to select items to put into the knapsack, and how to use the items with the greatest value It is divided into 01 backpack and complete backpack (complete backpack means that there are unlimited items available for each item)

(4) The problem here belongs to 01 knapsack, that is, each item can be placed at most, and infinite knapsack can be transformed into 01 knapsack

(5) The main idea of the algorithm is solved by dynamic programming. The ith item traversed each time is calculated according to w[i] and v[i]
Determine whether the item needs to be put into the backpack. That is, for a given n items, let v [], w[i] be the value and weight of the ith item respectively, and c be the capacity of the backpack. Let v[i][i] represent the maximum value that can be loaded into the backpack with capacity j in the first I items. Then we have the following results:

(1) v[i][0]=v[0][j]=0;    Indicates that the first row and the first column of the filled table are zero (2) When w [i] > J: v[i][j]=v[i-1][j] When the capacity of the newly added goods is greater than the capacity of the current backpack, the loading strategy of the previous cell is directly used (3) When J > = w [i]: v[i][j]=max{v[i-1][j],v[i]+v][i-1][j-w[i]]} When the newly added commodity capacity to be added is less than the capacity of the current backpack; Loading method: v[i-1][j]: This is the maximum value of the last cell loaded v[i]: indicates the value of the current commodity v[i-1][j-w[i]]: load I-1 commodities into the remaining space

graphic

 

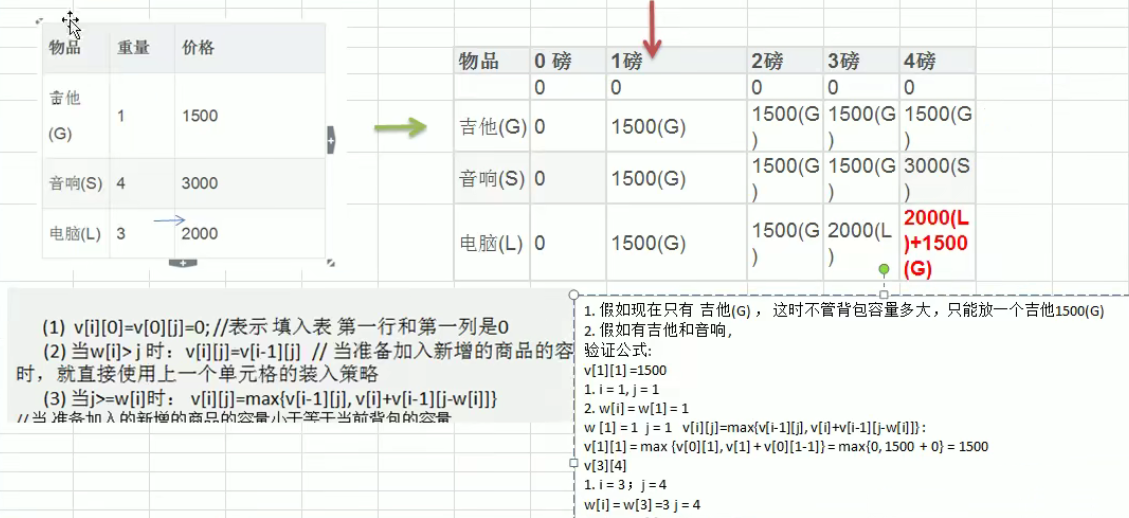
code implementation

package dynamic;

/**
 * Dynamic programming -- knapsack problem
 */
public class KnapsackProblem {
    public static void main(String[] args) {
        int[] w = {1, 4, 3};//Weight of articles
        int[] val = {1500, 3000, 2000}; //Value of goods
        int m = 4; //Backpack Capacity
        int n = val.length; //Number of items


        //Create a 2D array
        //v[i][j] represents the maximum value of the backpack with capacity of j in the first I items
        int[][] v = new int[n + 1][m + 1];
        //In order to record the placement of goods, we set up a two-dimensional array
        int[][] path = new int[n + 1][m + 1];

        //Initialize the first row and first column, which can not be processed in this program. The default is 0
        for (int i = 0; i < v.length; i++) {
            v[i][0] = 0; //Set the first column to 0
        }
        for (int i = 0; i < v[0].length; i++) {
            v[0][i] = 0;//Set the first row to 0
        }


        //The dynamic programming is processed according to the formula obtained above
        for (int i = 1; i < v.length; i++) { //Do not process the first row
            for (int j = 1; j < v[0].length; j++) { //Do not process the first column
                //formula
                if (w[i - 1] > j) { //Because our program I starts from 1, w[i] in the original formula is modified to w[i-1]
                    v[i][j] = v[i - 1][j];
                } else {
                    //explain
                    //Because our i starts from 1, the formula needs to be adjusted as follows
                    //v[i][j] = Math.max(v[i - 1][j], val[i - 1] + v[i - 1][j - w[i - 1]]);
                    //In order to record the goods stored in the backpack, we can't use the formula directly. We need to use if else to reflect the formula
                    if (v[i - 1][j] < val[i - 1] + v[i - 1][j - w[i - 1]]) {
                        v[i][j] = val[i - 1] + v[i - 1][j - w[i - 1]];
                        //Accumulate the current situation to path
                        path[i][j] = 1;
                    } else {
                        v[i][j] = v[i - 1][j];
                    }
                }
            }
        }


        //Output v to see the current situation
        for (int i = 0; i < v.length; i++) {
            for (int j = 0; j < v[i].length; j++) {
                System.out.print(v[i][j] + " ");
            }
            System.out.println();
        }
        //What we put in at the end of the output is the goods
        //Traversal path
//        for (int i = 0 ;i <path.length; i++){
//            for (int j=0 ;j<path[i].length; j++){
//                if(path[i][j]==1){
//                    System.out.println("put the% d item into the backpack \ n"+ i);
//                }
//            }
//        }

        //final result
        int i = path.length - 1; //Maximum subscript of row
        int j = path[0].length - 1;//Maximum subscript of column
        while (i > 0 && j > 0) {
            if (path[i][j] == 1) {
                System.out.printf("The first%d Put items into the backpack\n", i);
                j -= w[i - 1];
            }
            i--;
        }

    }
}

4: KMP algorithm

Application scenario - string matching problem

String matching problem:
(1) There is a string str1 = "Silicon Valley still Silicon Valley, you still Silicon Valley, you still Silicon Valley, you still Silicon Valley, you still silicon hello", and a substring str2 = "still Silicon Valley, you still silicon you"
(2) Now it is necessary to determine whether str1 contains str2. If it exists, it will return to the position where it first appears. If not,
Returns - 1
 

Violence matching algorithm

If we use the idea of violent matching and assume that str1 is now matched to position i and substring str2 is matched to position j, there are:+
(1) If the current character matches successfully (i.e. str1[i]== str2[li]), I + +, j + +, and continue to match the next character
(2) If mismatch (i.e. str1[i]! = str2[li]), let i=i-(j- 1), j=0. It is equivalent to I backtracking and J being set to 0 every time a match fails.
(3) If violence is used to solve the problem, there will be a lot of backtracking. Only move one bit at a time. If it doesn't match, move to the next bit and judge. It wastes a lot of time. (not feasible!)
(4) Violent matching algorithm implementation

code implementation
 

package kmp;

/**
 * Violent matching
 */
public class ViolenceMatch {

    public static void main(String[] args) {
        //Test violence matching algorithm
        String str1 = "Silicon valley still Silicon Valley you still Silicon Valley you still Silicon Valley you still Silicon Valley you still silicon hello";
        String str2 = "Shang Silicon Valley you Shang Silicon Valley you";
        int index = violenceMatch(str1, str2);
        System.out.println("index=" + index);
    }

    //Implementation of violence matching algorithm
    public static int violenceMatch(String str1, String str2) {
        char[] s1 = str1.toCharArray();
        char[] s2 = str2.toCharArray();

        int s1Len = s1.length;
        int s2Len = s2.length;

        int i = 0; //The i index points to s1
        int j = 0; //The j index points to s2
        while (i < s1Len && j < s2Len) { //Ensure that the matching does not exceed the limit

            if (s1[i] == s2[j]) { //Match successful
                i++;
                j++;
            } else { //No match succeeded
                i = i - (j - 1);
                j = 0;
            }
        }
        //Judge whether the match is successful
        if (j == s2Len) {
            return i - j;
        } else {
            return -1;
        }
    }
}

Introduction to KMP algorithm

(1) KMP is a classical algorithm to solve whether the pattern string has appeared in the text string, and if so, the earliest position
(2) Knuth Morris Pratt string search algorithm, referred to as "KMP algorithm" for short, is often used to find the occurrence position of a pattern string P in a text string S. This algorithm was jointly published by dopad Knuth, Vaughan Pratt and James H. Morris in 1977, so the algorithm was named after the surnames of these three people
(3) The KMP algorithm uses the previously judged information to save the length of the longest common subsequence in the pattern string through a next array. During each backtracking, the previous matching position is found through the next array, saving a lot of calculation time
(4) References: https://www.cnblogs.com/ZuoAndFutureGirl/p/9028287.html
 

Best application of KMP algorithm - string matching problem

>String matching problem:
(1) There is a string STR1 = "BBC abcdab abcdabde", and a substring str2="ABCDABD"
(2) Now it is necessary to determine whether str1 contains str2. If it exists, it returns the position where it first appears. If not, it returns - 1
(3) Requirements: KMP algorithm is used to complete judgment, and simple violent matching algorithm cannot be used

code implementation

package kmp;

import java.util.Arrays;

/**
 * KMP algorithm
 */
public class KMPAlgorithm {

    public static void main(String[] args) {

        String str1 = "BBC ABCDAB ABCDABCDABDE";
        String str2 = "ABCDABD";
        //String str2 = "BBC";

        int[] next = kmpNext("ABCDABD");
        System.out.println("next=" + Arrays.toString(next));

        int index = kmpSearch(str1, str2, next);
        System.out.println("index" + index);
    }


    /**
     * Write our kmp search algorithm
     *
     * @param str1 Source string
     * @param str2 String to search
     * @param next The partial matching table is the partial matching corresponding to the string
     * @return If it is - 1, there is no match. Otherwise, the first matching position is returned
     */
    public static int kmpSearch(String str1, String str2, int[] next) {
        //ergodic
        for (int i = 0, j = 0; i < str1.length(); i++) {

            //STR1. Needs to be processed charAt(i)!=  str2. Charat (j), to adjust the size of j
            //Core points of KMP algorithm
            while (j > 0 && str1.charAt(i) != str2.charAt(j)) {
                j = next[j - 1];
            }
            if (str1.charAt(i) == str2.charAt(j)) {
                j++;
            }
            if (j == str2.length()) {
                //eureka
                return i - j + 1;
            }
        }
        return -1;

    }

    //Gets the partial matching value table of a string (string)
    public static int[] kmpNext(String dest) {
        //Create a next array to hold some matching values
        int[] next = new int[dest.length()];
        next[0] = 0; //If the string length is 1, the matching value is 0
        for (int i = 1, j = 0; i < dest.length(); i++) {
            //When dest charAt(i)!= dest. Charat (J), we need to get a new j from next[j-1]
            //Until we found out when dest charAt(i)==dest. Charat (J) is established before exiting
            //This is the core of kmp algorithm
            while (j > 0 && dest.charAt(i) != dest.charAt(j)) {
                j = next[j - 1];

            }
            //When dest charAt(i)==dest. When charat (J) is satisfied, the partial matching value is + 1
            if (dest.charAt(i) == dest.charAt(j)) {
                j++;
            }
            next[i] = j;
        }
        return next;

    }
}

5: Greedy algorithm

Application scenario - set coverage problem

It is assumed that there are the following broadcasting stations that need to pay and the areas that can be covered by the broadcasting station signal How to select the least number of broadcasting stations so that all regions can receive signals

Introduction to greedy algorithm

(1) Greedy algorithm (greedy algorithm) refers to the algorithm that takes the best or optimal (i.e. the most favorable) choice in each step when solving the problem, so as to lead to the best or optimal result

(2) The results obtained by greedy algorithm are not necessarily the optimal results (sometimes the optimal solution), but they are relatively approximate (close) to the optimal results

Best application of greedy algorithm - set coverage

Train of thought analysis:
How to find the set of broadcasting stations covering all regions? It is implemented by exhaustive method to list the set of each possible broadcasting station, which is called power set. Assuming that there are n broadcasting stations in total, there are 2-1 broadcasting stations in total. It is assumed that 10 subsets can be calculated per second, as shown in the figure: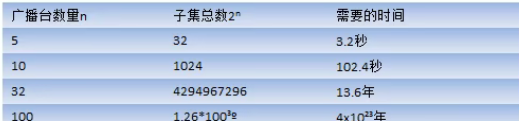

Train of thought analysis:
>Greedy algorithm with high efficiency:
At present, there is no algorithm that can quickly calculate the prepared value. Using greedy algorithm, we can get a very close solution with high efficiency. In terms of policy, the minimum set covering all regions is required:
(1) Traverse all radio stations and find a station that covers the most uncovered areas (this station may contain some covered areas, but it doesn't matter)
(2) Add the radio station to a collection (such as ArrayList) and try to remove the areas covered by the radio station in the next comparison.
(3) Repeat step 1 until all areas are covered

Analysis diagram

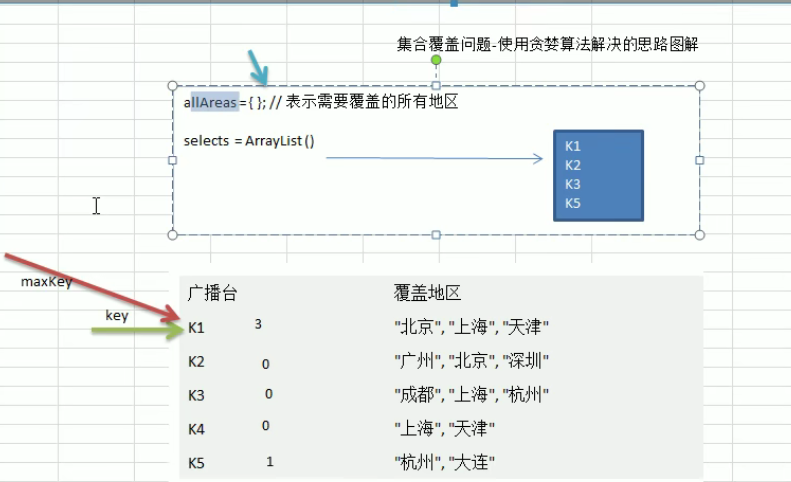
Code implementation:

package greedy;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;

public class GreedyAlgorithm {
    public static void main(String[] args) {
        //Create radio stations and put them into Map for management
        HashMap<String, HashSet> broadcats = new HashMap<String, HashSet>();
        //Put each radio station into broadcasts
        HashSet<String> hashSet1 = new HashSet<>();
        hashSet1.add("Beijing");
        hashSet1.add("Shanghai");
        hashSet1.add("Tianjin");

        HashSet<String> hashSet2 = new HashSet<>();
        hashSet2.add("Guangzhou");
        hashSet2.add("Beijing");
        hashSet2.add("Shenzhen");


        HashSet<String> hashSet3 = new HashSet<>();
        hashSet3.add("Chengdu");
        hashSet3.add("Shanghai");
        hashSet3.add("Hangzhou");

        HashSet<String> hashSet4 = new HashSet<>();
        hashSet4.add("Shanghai");
        hashSet4.add("Tianjin");

        HashSet<String> hashSet5 = new HashSet<>();
        hashSet5.add("Hangzhou");
        hashSet5.add("Dalian");

        //Add to map
        broadcats.put("K1", hashSet1);
        broadcats.put("K2", hashSet2);
        broadcats.put("K3", hashSet3);
        broadcats.put("K4", hashSet4);
        broadcats.put("K5", hashSet5);

        //allAreas stores all regions
        HashSet<String> allAreas = new HashSet<>();
        allAreas.add("Beijing");
        allAreas.add("Shanghai");
        allAreas.add("Tianjin");
        allAreas.add("Guangzhou");
        allAreas.add("Shenzhen");
        allAreas.add("Chengdu");
        allAreas.add("Hangzhou");
        allAreas.add("Dalian");

        //Create an ArrayList to store the selected radio station collection
        ArrayList<String> selects = new ArrayList<>();

        //Define a temporary set to store the intersection of radio coverage area and non coverage area during traversal
        HashSet<String> tempSet = new HashSet<>();

        //Define maxKey and save it in one traversal process. It can cover the radio station key corresponding to the largest uncovered area
        String maxKey = null;
        //If maxKye is not null, it will be added to the selections
        while (allAreas.size() != 0) { //If allAreas is not 0, it means that all regions have not been covered
            //Each while operation requires
            maxKey = null;

            //Traverse the broadcasts and take out the key
            for (String key : broadcats.keySet()) {
                //Every time
                tempSet.clear();
                //The area that this key can cover at present
                HashSet<String> areas = broadcats.get(key);
                tempSet.addAll(areas);
                //Find the intersection of tempSet and allAreas set, and the intersection will be assigned to tempSet
                tempSet.retainAll(allAreas);
                //If the current collection contains more uncovered regions than the collection region pointed to by the maxKey
                //You need to reset the maxKey
                //It reflects the characteristics of greedy algorithm
                if (tempSet.size() > 0 && (maxKey == null || tempSet.size() > broadcats.get(maxKey).size())) {
                    maxKey = key;
                }
            }
            //maxKey != null, you should add maxkey to selections
            if (maxKey != null) {
                selects.add(maxKey);
                //Remove the area covered by the radio station pointed to by maKey from allAreas
                allAreas.removeAll(broadcats.get(maxKey));
            }

        }
        System.out.println("The selection result is" + selects);//k1 k2 k3 k5
    }
}

Greedy algorithm considerations and details

(1) The results obtained by greedy algorithm are not necessarily the optimal results (sometimes the optimal solution), but they are relatively approximate (close) to the optimal solution
(2) For example, the algorithm in the above question selects K1, K2, K3 and K5, which covers all regions
(3) However, we found that K2, K3, K4 and K5 can also cover all regions. If the use cost of K2 is lower than K1, then
Well, K1,K2,K3,K5 in our last question satisfy the condition, but they are not optimal