Basic part of tree structure
1, Binary tree
1. Why do you need a tree data structure
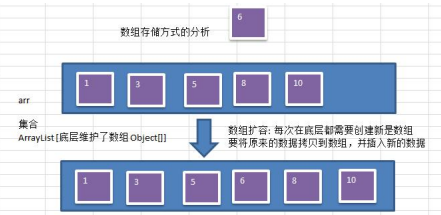
1.1 analysis of array storage mode
Advantages: it is fast to access elements by subscript. For ordered arrays, binary search can also be used to improve the retrieval speed.
Disadvantages: if a specific value is to be retrieved, or the inserted value (in a certain order) will move as a whole, which is inefficient [schematic]
Draw the operation diagram:
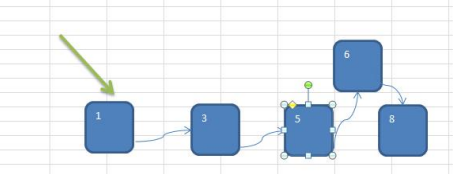
1.2 analysis of chain storage mode
Advantages: the array storage method is optimized to a certain extent (for example, if you insert a numeric node, you only need to link the inserted node to the linked list, and the deletion efficiency is also very good).
Disadvantages: when retrieving, the efficiency is still low, for example (to retrieve a value, you need to traverse from the beginning of the node)
Operation diagram:
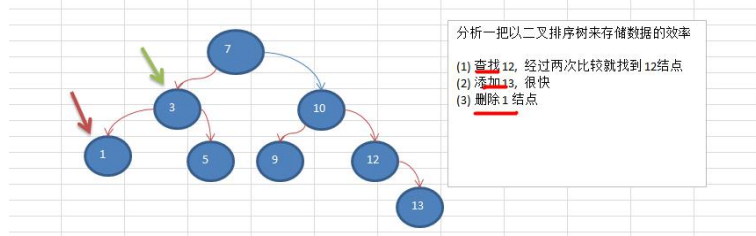
1.3 analysis of tree storage mode
It can improve the efficiency of data storage and reading. For example, using binary sort tree can not only ensure the speed of data retrieval, but also ensure the speed of data insertion, deletion and modification.
Case: [7, 3, 10, 1, 5, 9, 12]
2. Schematic diagram of tree
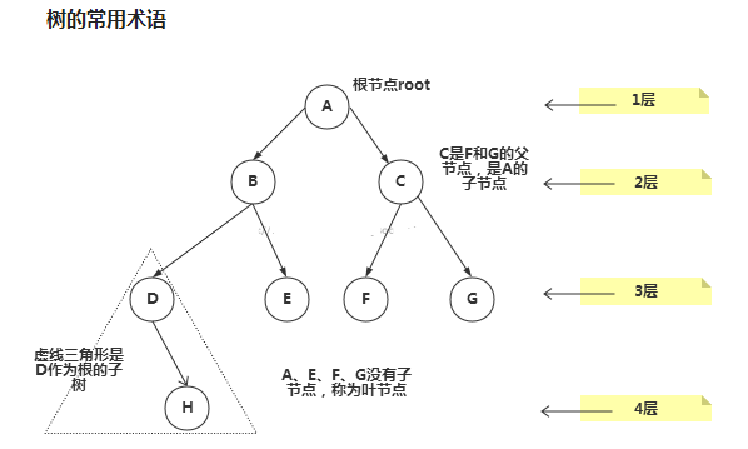
Common terms for trees(Understand in combination with schematic diagram): 1.node 2.Root node 3.Parent node 4.Child node 5.Leaf node (Nodes without child nodes) 6.Weight of node(Node value) 7.route(from root Node finds the route of the node) 8.layer 9.subtree 10.Tree height(Max layers ) 11.forest :Many subtrees form a forest
3. Concept of binary tree
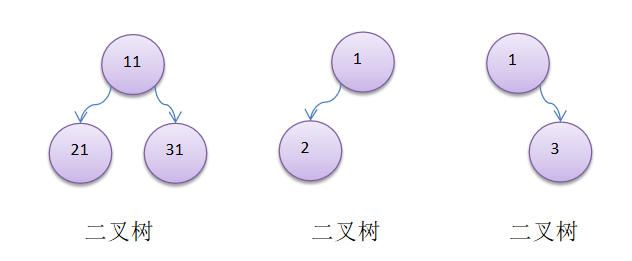
- There are many kinds of trees, and each node can only have two child nodes at most. One form is called binary tree.
- The child nodes of binary tree are divided into left node and right node
- Sketch Map
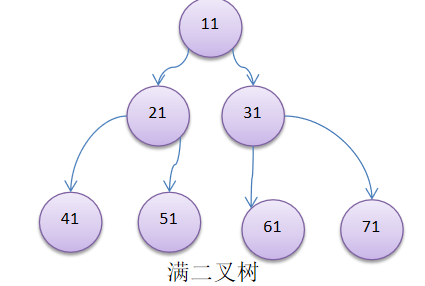
- If all leaf nodes of the binary tree are in the last layer, and the total number of nodes = 2 ^ n - 1, n is the number of layers, then we call it a full binary tree.
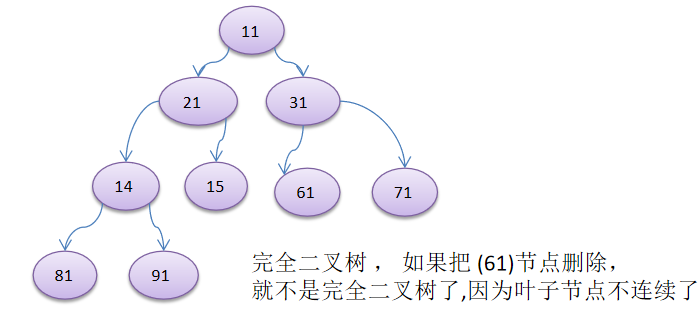
- If all leaf nodes of the binary tree are in the last or penultimate layer, and the leaf nodes of the last layer are continuous on the left and the leaf nodes of the penultimate layer are continuous on the right, we call it a complete binary tree
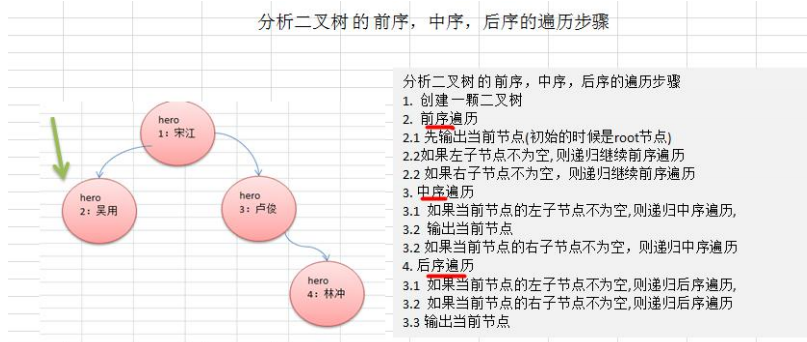
4. Description of binary tree traversal
Use preorder, inorder and postorder to traverse the following binary tree
- Preorder traversal: first output the parent node, and then traverse the left and right subtrees
-
Middle order traversal: first traverse the left subtree, then output the parent node, and then traverse the right subtree
-
Post order traversal: first traverse the left subtree, then traverse the right subtree, and finally output the parent node
-
Summary: see the order of output parent nodes to determine whether it is pre order, middle order or post order
4.1 application examples of binary tree traversal (pre order, middle order and post order)
code implementation
//Method of writing preorder traversal
public void preOrder() {
System.out.println(this); //Output parent node first
//Recursive pre order traversal to the left subtree
if(this.left != null) {
this.left.preOrder();
}
//Recursive right subtree preorder traversal
if(this.right != null) {
this.right.preOrder();
}
}
//Medium order traversal
public void infixOrder() {
//Recursive traversal to the middle order of the left subtree
if(this.left != null) {
this.left.infixOrder();
}
//Output parent node
System.out.println(this);
//Recursive traversal in right subtree
if(this.right != null) {
this.right.infixOrder();
}
}
//Postorder traversal
public void postOrder() {
if(this.left != null) {
this.left.postOrder();
}
if(this.right != null) {
this.right.postOrder();
}
System.out.println(this);
}
test
public class BinaryTreeDemo {
public static void main(String[] args) {
//First you need to create a binary tree
BinaryTree binaryTree = new BinaryTree();
//Create required nodes
HeroNode root = new HeroNode(1, "Song Jiang");
HeroNode node2 = new HeroNode(2, "Wu Yong");
HeroNode node3 = new HeroNode(3, "Lu Junyi");
HeroNode node4 = new HeroNode(4, "Lin Chong");
HeroNode node5 = new HeroNode(5, "Guan Sheng");
//Note: we first create the binary tree manually, and then we learn to create the binary tree recursively
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
//test
System.out.println("Preorder traversal"); // 1,2,3,5,4
binaryTree.preOrder();
//test
System.out.println("Medium order traversal");
binaryTree.infixOrder(); // 2,1,5,3,4
System.out.println("Postorder traversal");
binaryTree.postOrder(); // 2,5,4,3,1
}
}
//Define BinaryTree binary tree
class BinaryTree {
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
//Preorder traversal
public void preOrder() {
if(this.root != null) {
this.root.preOrder();
}else {
System.out.println("Binary tree is empty and cannot be traversed");
}
}
//Medium order traversal
public void infixOrder() {
if(this.root != null) {
this.root.infixOrder();
}else {
System.out.println("Binary tree is empty and cannot be traversed");
}
}
//Postorder traversal
public void postOrder() {
if(this.root != null) {
this.root.postOrder();
}else {
System.out.println("Binary tree is empty and cannot be traversed");
}
}
}
//Create the HeroNode node first
class HeroNode {
private int no;
private String name;
private HeroNode left; //Default null
private HeroNode right; //Default null
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
//Method of writing preorder traversal
public void preOrder() {
System.out.println(this); //Output parent node first
//Recursive pre order traversal to the left subtree
if(this.left != null) {
this.left.preOrder();
}
//Recursive right subtree preorder traversal
if(this.right != null) {
this.right.preOrder();
}
}
//Medium order traversal
public void infixOrder() {
//Recursive traversal to the middle order of the left subtree
if(this.left != null) {
this.left.infixOrder();
}
//Output parent node
System.out.println(this);
//Recursive traversal in right subtree
if(this.right != null) {
this.right.infixOrder();
}
}
//Postorder traversal
public void postOrder() {
if(this.left != null) {
this.left.postOrder();
}
if(this.right != null) {
this.right.postOrder();
}
System.out.println(this);
}
}
5. Binary tree - find the specified node
requirement
- Please write pre order search, middle order search and post order search methods.
- Three search methods are used to find the node with heroNO = 5
- And analyze various search methods, and compare how many times
- Train of thought analysis diagram
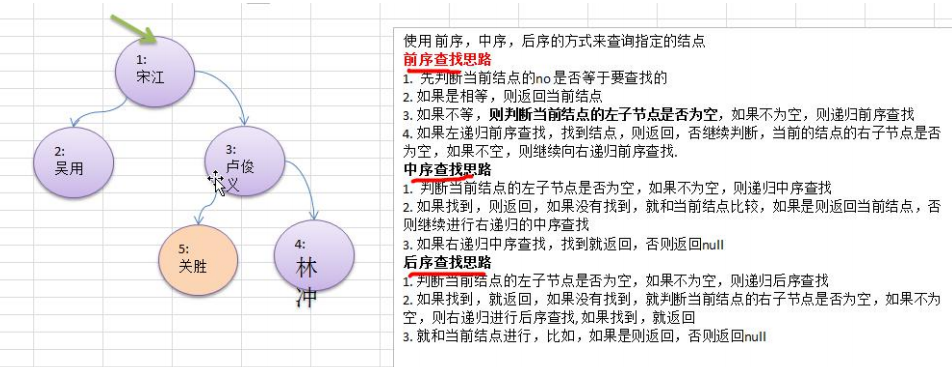
- code implementation
//Preorder traversal search
/**
*
* @param no Find no
* @return If found, the Node is returned. If not found, null is returned
*/
public HeroNode preOrderSearch(int no) {
System.out.println("Enter preorder traversal");
//Compare whether the current node is
if(this.no == no) {
return this;
}
//1. Judge whether the left child node of the current node is empty. If not, recursive preorder search
//2. If the left recursive preamble finds a node, it returns
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if(resNode != null) {//That means we found the left subtree
return resNode;
}
//1. Left recursive preorder search. If a node is found, it returns. Continue to judge whether or not,
//2. Whether the right child node of the current node is empty. If it is not empty, continue to search in the right recursive preamble
if(this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
//Middle order traversal search
public HeroNode infixOrderSearch(int no) {
//Judge whether the left child node of the current node is empty. If it is not empty, search in recursive middle order
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("Enter middle order search");
//If found, it returns. If not found, it is compared with the current node. If yes, it returns the current node
if(this.no == no) {
return this;
}
//Otherwise, continue the middle order search of right recursion
if(this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
//Postorder traversal search
public HeroNode postOrderSearch(int no) {
//Judge whether the left child node of the current node is empty. If it is not empty, it will be searched recursively
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if(resNode != null) {//Description found in the left subtree
return resNode;
}
//If the left subtree is not found, the right subtree recursively performs a post order traversal search
if(this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("Enter post order search");
//If the left and right subtrees are not found, compare the current node
if(this.no == no) {
return this;
}
return resNode;
}
test
public class BinaryTreeDemo {
public static void main(String[] args) {
//First you need to create a binary tree
BinaryTree binaryTree = new BinaryTree();
//Create required nodes
HeroNode root = new HeroNode(1, "Song Jiang");
HeroNode node2 = new HeroNode(2, "Wu Yong");
HeroNode node3 = new HeroNode(3, "Lu Junyi");
HeroNode node4 = new HeroNode(4, "Lin Chong");
HeroNode node5 = new HeroNode(5, "Guan Sheng");
//Note: we first create the binary tree manually, and then we learn to create the binary tree recursively
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
//Preorder traversal
//Number of preorder traversals: 4
System.out.println("Preorder traversal mode~~~");
HeroNode resNode = binaryTree.preOrderSearch(5);
if (resNode != null) {
System.out.printf("Yes, the information is no=%d name=%s", resNode.getNo(), resNode.getName());
} else {
System.out.printf("Can't find no = %d Hero of", 5);
}
//Middle order traversal search
//Middle order traversal 3 times
System.out.println("Middle order traversal mode~~~");
HeroNode resNode = binaryTree.infixOrderSearch(5);
if (resNode != null) {
System.out.printf("Yes, the information is no=%d name=%s", resNode.getNo(), resNode.getName());
} else {
System.out.printf("Can't find no = %d Hero of", 5);
}
//Post order traversal search
//The number of subsequent traversal lookups is 2
System.out.println("postorder traversal ~~~");
HeroNode resNode = binaryTree.postOrderSearch(5);
if (resNode != null) {
System.out.printf("Yes, the information is no=%d name=%s", resNode.getNo(), resNode.getName());
} else {
System.out.printf("Can't find no = %d Hero of", 5);
}
}
}
//Define BinaryTree
class BinaryTree {
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
//Preorder traversal
public HeroNode preOrderSearch(int no) {
if(root != null) {
return root.preOrderSearch(no);
} else {
return null;
}
}
//Medium order traversal
public HeroNode infixOrderSearch(int no) {
if(root != null) {
return root.infixOrderSearch(no);
}else {
return null;
}
}
//Postorder traversal
public HeroNode postOrderSearch(int no) {
if(root != null) {
return this.root.postOrderSearch(no);
}else {
return null;
}
}
}
//Create the HeroNode node first
class HeroNode {
private int no;
private String name;
private HeroNode left; //Default null
private HeroNode right; //Default null
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
//Preorder traversal search
/**
*
* @param no Find no
* @return If found, the Node is returned. If not found, null is returned
*/
public HeroNode preOrderSearch(int no) {
System.out.println("Enter preorder traversal");
//Compare whether the current node is
if(this.no == no) {
return this;
}
//1. Judge whether the left child node of the current node is empty. If not, recursive preorder search
//2. If the left recursive preamble finds a node, it returns
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if(resNode != null) {//That means we found the left subtree
return resNode;
}
//1. Left recursive preorder search. If a node is found, it returns. Continue to judge whether or not,
//2. Whether the right child node of the current node is empty. If it is not empty, continue to search in the right recursive preamble
if(this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
//Middle order traversal search
public HeroNode infixOrderSearch(int no) {
//Judge whether the left child node of the current node is empty. If it is not empty, search in recursive middle order
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("Enter middle order search");
//If found, it returns. If not found, it is compared with the current node. If yes, it returns the current node
if(this.no == no) {
return this;
}
//Otherwise, continue the middle order search of right recursion
if(this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
//Postorder traversal search
public HeroNode postOrderSearch(int no) {
//Judge whether the left child node of the current node is empty. If it is not empty, it will be searched recursively
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if(resNode != null) {//Description found in the left subtree
return resNode;
}
//If the left subtree is not found, the right subtree recursively performs a post order traversal search
if(this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("Enter post order search");
//If the left and right subtrees are not found, compare the current node
if(this.no == no) {
return this;
}
return resNode;
}
}
6. Binary tree - delete node
requirement
-
If the deleted node is a leaf node, delete the node
-
If the deleted node is a non leaf node, the subtree is deleted
-
Test, delete No. 5 leaf node and No. 3 subtree
-
Complete deletion thought analysis
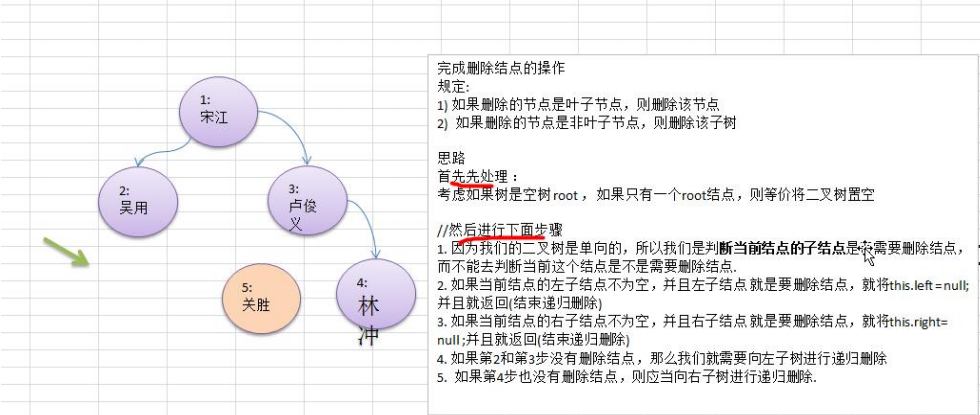
- code implementation
//Delete Vertex
public void delNode(int no) {
if(root != null) {
//If there is only one root node, judge whether root is to delete the node immediately
if(root.getNo() == no) {
root = null;
} else {
//Recursive deletion
root.delNode(no);
}
}else{
System.out.println("The tree is empty and cannot be deleted~");
}
}
//Recursively delete nodes
//1. If the deleted node is a leaf node, delete the node
//2. If the deleted node is a non leaf node, delete the subtree
public void delNode(int no) {
//thinking
/*
* 1. Because our binary tree is unidirectional, we judge whether the child node of the current node needs to be deleted, but not whether the current node needs to be deleted
2. If the left child node of the current node is not empty and the left child node is to delete the node, set this left = null; And return (end recursive deletion)
3. If the right child node of the current node is not empty and the right child node is to delete the node, set this right= null ; And return (end recursive deletion)
4. If the node is not deleted in steps 2 and 3, we need to delete it recursively to the left subtree
5. If the node is not deleted in step 4, it should be deleted recursively to the right subtree
*/
//2. If the left child node of the current node is not empty and the left child node is to delete the node, set this left = null; And return (end recursive deletion)
if(this.left != null && this.left.no == no) {
this.left = null;
return;
}
//3. If the right child node of the current node is not empty and the right child node is to delete the node, set this right= null ; And return (end recursive deletion)
if(this.right != null && this.right.no == no) {
this.right = null;
return;
}
//4. We need to delete recursively to the left subtree
if(this.left != null) {
this.left.delNode(no);
}
//5. The right subtree should be deleted recursively
if(this.right != null) {
this.right.delNode(no);
}
}
Complete test
public class BinaryTreeDemo {
public static void main(String[] args) {
//First you need to create a binary tree
BinaryTree binaryTree = new BinaryTree();
//Create required nodes
HeroNode root = new HeroNode(1, "Song Jiang");
HeroNode node2 = new HeroNode(2, "Wu Yong");
HeroNode node3 = new HeroNode(3, "Lu Junyi");
HeroNode node4 = new HeroNode(4, "Lin Chong");
HeroNode node5 = new HeroNode(5, "Guan Sheng");
//Note: we first create the binary tree manually, and then we learn to create the binary tree recursively
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
//Test a delete node
System.out.println("Before deletion,Preorder traversal");
binaryTree.preOrder(); // 1,2,3,5,4
binaryTree.delNode(5);
//binaryTree.delNode(3);
System.out.println("After deletion, the preamble traverses");
binaryTree.preOrder(); // 1,2,3,4
}
}
//Define BinaryTree
class BinaryTree {
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
//Delete Vertex
public void delNode(int no) {
if(root != null) {
//If there is only one root node, judge whether root is to delete the node immediately
if(root.getNo() == no) {
root = null;
} else {
//Recursive deletion
root.delNode(no);
}
}else{
System.out.println("The tree is empty and cannot be deleted~");
}
}
//Preorder traversal
public void preOrder() {
if(this.root != null) {
this.root.preOrder();
}else {
System.out.println("Binary tree is empty and cannot be traversed");
}
}
}
//Create the HeroNode node first
class HeroNode {
private int no;
private String name;
private HeroNode left; //Default null
private HeroNode right; //Default null
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
//Recursively delete nodes
//1. If the deleted node is a leaf node, delete the node
//2. If the deleted node is a non leaf node, delete the subtree
public void delNode(int no) {
//thinking
/*
* 1. Because our binary tree is unidirectional, we judge whether the child node of the current node needs to be deleted, but not whether the current node needs to be deleted
2. If the left child node of the current node is not empty and the left child node is to delete the node, set this left = null; And return (end recursive deletion)
3. If the right child node of the current node is not empty and the right child node is to delete the node, set this right= null ; And return (end recursive deletion)
4. If the node is not deleted in steps 2 and 3, we need to delete it recursively to the left subtree
5. If the node is not deleted in step 4, it should be deleted recursively to the right subtree
*/
//2. If the left child node of the current node is not empty and the left child node is to delete the node, set this left = null; And return (end recursive deletion)
if(this.left != null && this.left.no == no) {
this.left = null;
return;
}
//3. If the right child node of the current node is not empty and the right child node is to delete the node, set this right= null ; And return (end recursive deletion)
if(this.right != null && this.right.no == no) {
this.right = null;
return;
}
//4. We need to delete recursively to the left subtree
if(this.left != null) {
this.left.delNode(no);
}
//5. The right subtree should be deleted recursively
if(this.right != null) {
this.right.delNode(no);
}
}
//Method of writing preorder traversal
public void preOrder() {
System.out.println(this); //Output parent node first
//Recursive pre order traversal to the left subtree
if(this.left != null) {
this.left.preOrder();
}
//Recursive right subtree preorder traversal
if(this.right != null) {
this.right.preOrder();
}
}
}
6.1 thinking questions (after class exercises)
- If the node to be deleted is a non leaf node, now we don't want to delete the subtree with the non leaf node as the root node. We need to specify the rules if they are as follows:
- If the non leaf node A has only one child node B, the child node B replaces node A
- If the non leaf node A has A left child node B and A right child node C, let the left child node B replace node A.
//Recursively delete nodes
public void delNode1(int no) {
//2. If the left child node of the current node is not empty and the left child node is to delete the node, set this left = null; And return (end recursive deletion)
if(this.left != null && this.left.no == no) {
//Delete directly for leaf node
if(this.left.left == null && this.left.right == null) {
this.left = null;
//Only one child node is directly replaced
} else if(this.left.left != null && this.left.right == null) {
this.left = this.left.left;
}else if(this.left.left == null && this.left.right != null) {
this.left = this.left.right;
//There are two nodes, the left node is replaced, and the right node is inserted into the rightmost leaf node of the left node
}else if(this.left.left != null && this.left.right != null) {
HeroNode temp = this.left.right;
this.left = this.left.left;
HeroNode temp1 = this.left;
while (temp1.right != null){
temp1 = temp1.right;
}
temp1.right = temp;
}
return;
}
//3. If the right child node of the current node is not empty and the right child node is to delete the node, set this right= null ; And return (end recursive deletion)
if(this.right != null && this.right.no == no) {
//Delete directly for leaf node
if(this.right.left == null && this.right.right == null) {
this.right = null;
//Only one child node is directly replaced
} else if(this.right.left != null && this.right.right == null) {
this.right = this.right.left;
}else if(this.right.left == null && this.right.right != null) {
this.right = this.right.right;
//There are two nodes, the left node is replaced, and the right node is inserted into the rightmost leaf node of the left node
}else if(this.right.left != null && this.right.right != null) {
HeroNode temp = this.right.right;
this.right = this.right.left;
HeroNode temp1 = this.right;
while (temp1.right != null){
temp1 = temp1.right;
}
temp1.right = temp;
}
return;
}
//4. We need to delete recursively to the left subtree
if(this.left != null) {
this.left.delNode1(no);
}
//5. The right subtree should be deleted recursively
if(this.right != null) {
this.right.delNode1(no);
}
}
2, Sequential storage binary tree
1. The concept of sequential storage binary tree
1.1 basic description
From the perspective of data storage, array storage mode and tree storage mode can be converted to each other, that is, array can be converted into tree and tree can also be converted into array. See the following diagram.
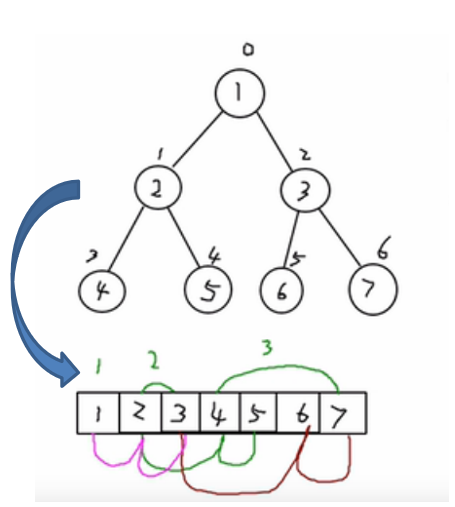
2. Features of sequential storage binary tree:
- Sequential binary trees usually only consider complete binary trees
- The left child node of the nth element is 2 * n + 1
- The right child node of the nth element is 2 * n + 2
- The parent node of the nth element is (n-1) / 2
- n: indicates the number of elements in the binary tree (starting with 0, as shown in the figure)
3. Sequential storage binary tree traversal
Requirements: give you an array {1,2,3,4,5,6,7}, which is required to be traversed in the way of binary tree preorder traversal. The result of preorder traversal should be
1,2,4,5,3,6,7
3.1 code implementation:
public class ArrBinaryTreeDemo {
public static void main(String[] args) {
int[] arr = { 1, 2, 3, 4, 5, 6, 7 };
//Create an ArrBinaryTree
ArrBinaryTree arrBinaryTree = new ArrBinaryTree(arr);
arrBinaryTree.preOrder(); // 1,2,4,5,3,6,7
}
}
//Write an ArrayBinaryTree to realize the traversal of sequential storage binary tree
class ArrBinaryTree {
private int[] arr;//An array that stores data nodes
public ArrBinaryTree(int[] arr) {
this.arr = arr;
}
//Reload preOrder
public void preOrder() {
this.preOrder(0);
}
//Write a method to complete the preorder traversal of the sequential storage binary tree
/**
*
* @param index Subscript of array
*/
public void preOrder(int index) {
//If the array is empty, or arr.length = 0
if(arr == null || arr.length == 0) {
System.out.println("The array is empty and cannot be traversed in the order before the binary tree");
}
//Output the current element
System.out.println(arr[index]);
//Left recursive traversal
if((index * 2 + 1) < arr.length) {
preOrder(2 * index + 1 );
}
//Right recursive traversal
if((index * 2 + 2) < arr.length) {
preOrder(2 * index + 2);
}
}
}
3.2 after class exercises
Complete the code of traversing the array in binary tree order and post order
//Overload postorder public void postOrder() { this.postOrder(0); System.out.println(); } // Write a method to complete the post order traversal of the sequential storage binary tree /** * * @ Subscript of param index array */ public void postOrder(int index) { // If the array is empty, or arr.length = 0 if(arr == null || arr.length == 0) { System.out.println("the array is empty and cannot be traversed according to the previous order of the binary tree"); } // Left recursive traversal if(index * 2 + 1 < arr.length){ postOrder(index * 2 + 1); } // Right recursive traversal if(index * 2 + 2 < arr.length){ postOrder(index * 2 + 2); } // Output the current element System.out.print(arr[index] + " "); } // Overload infixorder public void infixOrder() { this.infixOrder(0); System.out.println(); } // Write a method to complete the middle order traversal of the sequential storage binary tree /** * * @ Subscript of param index array */ public void infixOrder(int index) { // If the array is empty, or arr.length = 0 if(arr == null || arr.length == 0) { System.out.println("the array is empty and cannot be traversed according to the previous order of the binary tree"); } // Left recursive traversal if((index * 2 + 1) < arr.length) { infixOrder(2 * index + 1 ); } // Output the current element System.out.print(arr[index] + " "); // Right recursive traversal if((index * 2 + 2) < arr.length) { infixOrder(2 * index + 2); } }
4. Sequential storage of binary tree application examples
The heap sorting in the eight sorting algorithms will use the sequential storage binary tree.
3, Cued binary tree
3.1 let's look at one question first
The sequence {1,3,6,8,10,14} is constructed into a binary tree n+1=7
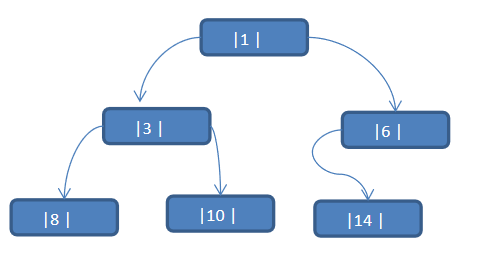
Problem analysis:
- When we traverse the above binary tree in middle order, the sequence is {8, 3, 10, 1, 6, 14}
- However, the left and right pointers of nodes 6, 8, 10 and 14 are not fully utilized
- What if we want to make full use of the left and right pointers of each node so that each node can point to its own front and rear nodes?
- Solution - clue binary tree
3.2 basic introduction to clue binary tree
- The binary list of N nodes contains n+1 [Formula 2n-(n-1)=n+1] empty finger needle fields. The null pointer field in the binary list is used to store pointers to the precursor and successor nodes of the node in a certain traversal order (this additional pointer is called "clue")
- This binary linked list with clues is called clue linked list, and the corresponding binary tree is called threaded binary tree. According to the different properties of clues, clue binary trees can be divided into three types: pre order clue binary trees, middle order clue binary trees and post order clue binary trees
- The previous node of a node is called the precursor node
- The next node of a node is called the successor node
3.3 application cases of clue binary tree
Application case description: apply the following binary tree to the middle order clue binary tree. The sequence traversed in middle order is {8, 3, 10, 1, 14, 6}
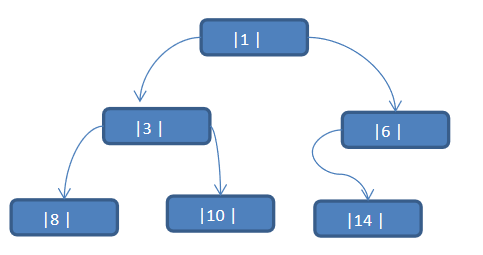
3.3.1 train of thought analysis:
Results of medium order traversal: {8, 3, 10, 1, 14, 6}
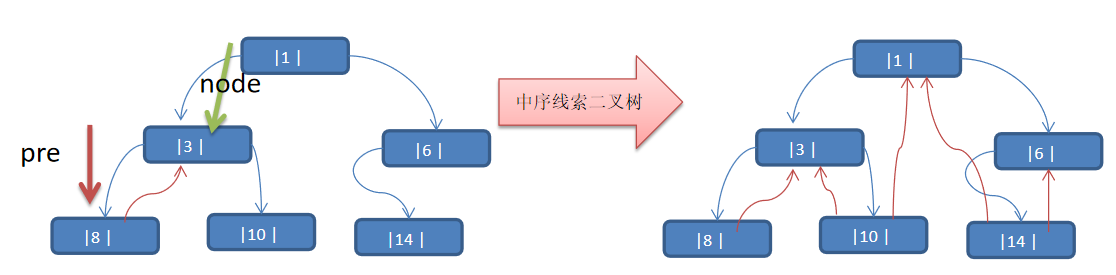
3.3.2 Description:
After cueing the binary tree, the attributes left and right of the Node are as follows:
- Left refers to the left subtree or the precursor node For example, ① node left points to the left subtree, while ⑩ node left points to the precursor node
- Right refers to the right subtree or the successor node. For example, ① node right refers to the right subtree, while ⑩ node right refers to the successor node
3.3.3 code implementation
//Write the method of medium order cueing of binary tree /** * * @ param node is the node that needs cueing at present */ public void threadedNodes(HeroNode node) { // If node==null, it cannot be threaded if(node==null) { return; } // (1) Cue left subtree first threadedNodes(node.getLeft()); // (2) Cue current node [difficult] // Handle the precursor node of the current node // Understand with 8 nodes // 8 nodes Left = null, 8 nodes leftType = 1 if(node.getLeft() == null) { // Let the left pointer of the current node point to the predecessor node node.setLeft(pre); // Modify the type of the left pointer of the current node to point to the predecessor node node.setLeftType(1); } // Processing successor nodes if (pre != null && pre.getRight() == null) { // Let the right pointer of the predecessor node point to the current node pre.setRight(node); // Modify the right pointer type of the precursor node pre.setRightType(1); } //!!! After each node is processed, the current node is the precursor node of the next node pre = node; // (3) Online right subtree threadedNodes(node.getRight()); }
test
public class ThreadedBinaryTreeDemo { public static void main(String[] args) { //Test the function of a medium order clue binary tree HeroNode root = new HeroNode(1, "tom"); HeroNode node2 = new HeroNode(3, "jack"); HeroNode node3 = new HeroNode(6, "smith"); HeroNode node4 = new HeroNode(8, "mary"); HeroNode node5 = new HeroNode(10, "king"); HeroNode node6 = new HeroNode(14, "dim"); // Binary tree, we will create it recursively later. Now it is simple to create it manually root.setLeft(node2); root.setRight(node3); node2.setLeft(node4); node2.setRight(node5); node3.setLeft(node6); // Sequential cueing in testing ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree(); threadedBinaryTree.setRoot(root); threadedBinaryTree.threadedNodes(); // Test: test with node 10 HeroNode leftNode = node5.getLeft(); HeroNode rightNode = node5.getRight(); System. out. Println ("the precursor node of node 10 is =" + leftnode)// three System. out. Println ("the successor node of node 10 is =" + rightnode)// one }}// Define threadedbinarytree, a binary tree class ThreadedBinaryTree that implements the cue function{ private HeroNode root; // In order to realize cueing, you need to create a pointer to the precursor node pointing to the current node // In recursive cueing, pre always retains the previous node private HeroNode pre = null; public void setRoot(HeroNode root) { this.root = root; } // Overload a threadednodes method public void threadedNodes() { this.threadedNodes(root); } // Write the method of medium order cueing of binary tree /** * * @ param node is the node that needs cueing at present */ public void threadedNodes(HeroNode node) { // If node==null, it cannot be threaded if(node==null) { return; } // (1) Cue left subtree first threadedNodes(node.getLeft()); // (2) Cue current node [difficult] // Handle the precursor node of the current node // Understand with 8 nodes // 8 nodes Left = null, 8 nodes leftType = 1 if(node.getLeft() == null) { // Let the left pointer of the current node point to the predecessor node node.setLeft(pre); // Modify the type of the left pointer of the current node to point to the predecessor node node.setLeftType(1); } // Processing successor nodes if (pre != null && pre.getRight() == null) { // Let the right pointer of the predecessor node point to the current node pre.setRight(node); // Modify the right pointer type of the precursor node pre.setRightType(1); } //!!! After each node is processed, the current node is the precursor node of the next node pre = node; // (3) Online right subtree threadedNodes(node.getRight()); }}// Create the heronode node class first{ private int no; private String name; private HeroNode left; // Default null private HeroNode right; // Default null // explain // 1. If leftType == 0, it refers to the left subtree; if 1, it refers to the precursor node // 2. If rightType == 0, it means pointing to the right subtree; if 1, it means pointing to the successor node private int leftType; private int rightType; public int getLeftType() { return leftType; } public void setLeftType(int leftType) { this.leftType = leftType; } public int getRightType() { return rightType; } public void setRightType(int rightType) { this.rightType = rightType; } public HeroNode(int no, String name) { this.no = no; this.name = name; } public int getNo() { return no; } public void setNo(int no) { this.no = no; } public String getName() { return name; } public void setName(String name) { this.name = name; } public HeroNode getLeft() { return left; } public void setLeft(HeroNode left) { this.left = left; } public HeroNode getRight() { return right; } public void setRight(HeroNode right) { this.right = right; } @ Override public String toString() { return "HeroNode [no=" + no + ", name=" + name + "]"; } }
3.4 traversing threaded binary tree
- Description: traverse the previously ordered threaded binary tree
- Analysis: because the direction of each node changes after cueing, the original traversal method cannot be used. At this time, a new method needs to be used to traverse the cued binary tree. Each node can be traversed by linear method, so there is no need to use recursive method, which also improves the efficiency of traversal. The order of traversal should be consistent with that of middle order traversal.
- code:
//Method of traversing cued binary tree public void threadedList() { // Define a variable to store the currently traversed node, starting from root HeroNode node = root; while(node != null) { // Loop to find the node with leftType==1, and the first to find is 8 nodes // The following changes with traversal, because when leftType==1, it indicates that the node is threaded // Effective nodes after processing while(node.getLeftType() == 0) { node = node.getLeft(); } // Print the current node System.out.println(node); // If the right pointer of the current node points to the subsequent node, it will be output all the time while(node.getRightType() == 1) { // Gets the successor node of the current node node = node.getRight(); System.out.println(node); } // Replace this traversal node node = node.getRight(); } }
Homework after class: write pre order clue binary tree and post order clue binary tree. Their analysis ideas are similar
Preordered cued binary tree
public void preThreadedNodes() { this.preThreadedNodes(root); }//Write a method for preorder cueing of binary tree public void preThreadedNodes(HeroNode node) { // If node==null, it cannot be threaded if(node==null) { return; } // Handle the precursor node of the current node // Understand with 8 nodes // 8 nodes Left = null, 8 nodes leftType = 1 if(node.getLeft() == null) { // Let the left pointer of the current node point to the predecessor node node.setLeft(pre); // Modify the type of the left pointer of the current node to point to the predecessor node node.setLeftType(1); } // Processing successor nodes if (pre != null && pre.getRight() == null) { // Let the right pointer of the predecessor node point to the current node pre.setRight(node); // Modify the right pointer type of the precursor node pre.setRightType(1); } //!!! After each node is processed, the current node is the precursor node of the next node pre = node; if(node.getLeftType() == 0) { preThreadedNodes(node.getLeft()); } if(node.getRightType() == 0) { preThreadedNodes(node.getRight()); } }// Method of traversing cued binary tree public void preThreadedList() { // Define a variable to store the currently traversed node, starting from root HeroNode node = root; while(node != null) { while(node.getLeftType() == 0) { // Print the current node System.out.println(node); node = node.getLeft(); } // Print the current node System.out.println(node); node = node.getRight(); } }
Post ordered cued binary tree
public void postThreadedNodes(HeroNode node) { if(node == null) return; if(node.getLeftType() == 0){ postThreadedNodes(node.getLeft()); } if(node.getRightType() == 0){ postThreadedNodes(node.getRight()); } if(node.getLeft() == null){ node.setLeft(pre); node.setLeftType(1); } if(pre != null && pre.getRight() == null){ pre.setRight(node); pre.setRightType(1); } pre = node; } public void postThreadedList() { HeroNode node = root; while (node != null && node.getLeftType() == 0){ node = node.getLeft(); } HeroNode pre = null; while (node != null){ if(node.getRightType() == 1){ System.out.println(node); pre = node; node = node.getRight(); }else { if(node.getRight() == pre){ System.out.println(node); if(node == root){ return; } pre = node; node = node.getParent(); }else { node = node.getRight(); while (node != null && node.getLeftType() == 0){ node = node.getLeft(); } } } } }