Data structure and algorithm

statement:Main sources of notes data structure and algorithm[Qingdao University-Wang Zhuo],For review of data structures
https://www.bilibili.com/video/BV1nJ411V7bd

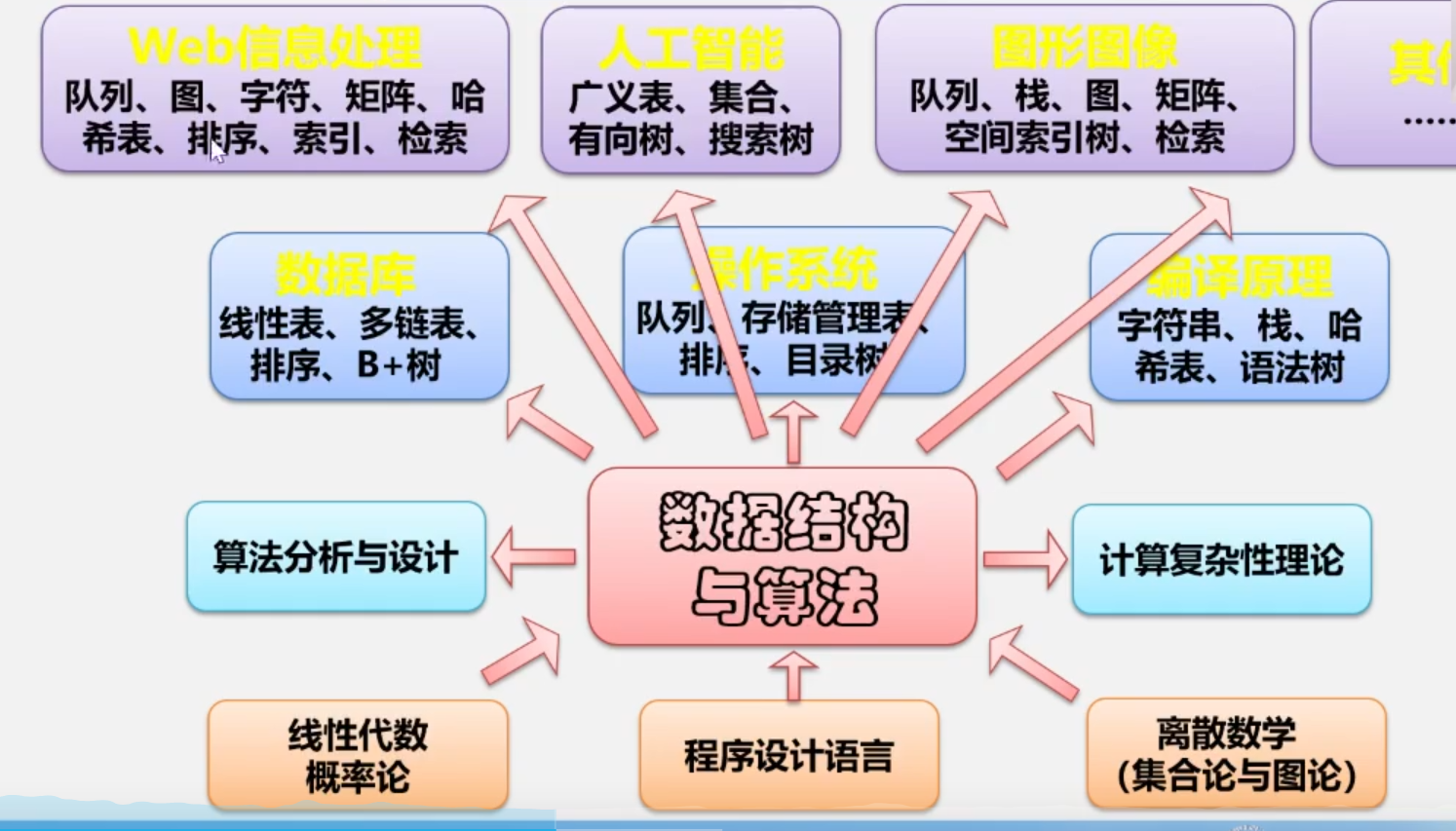
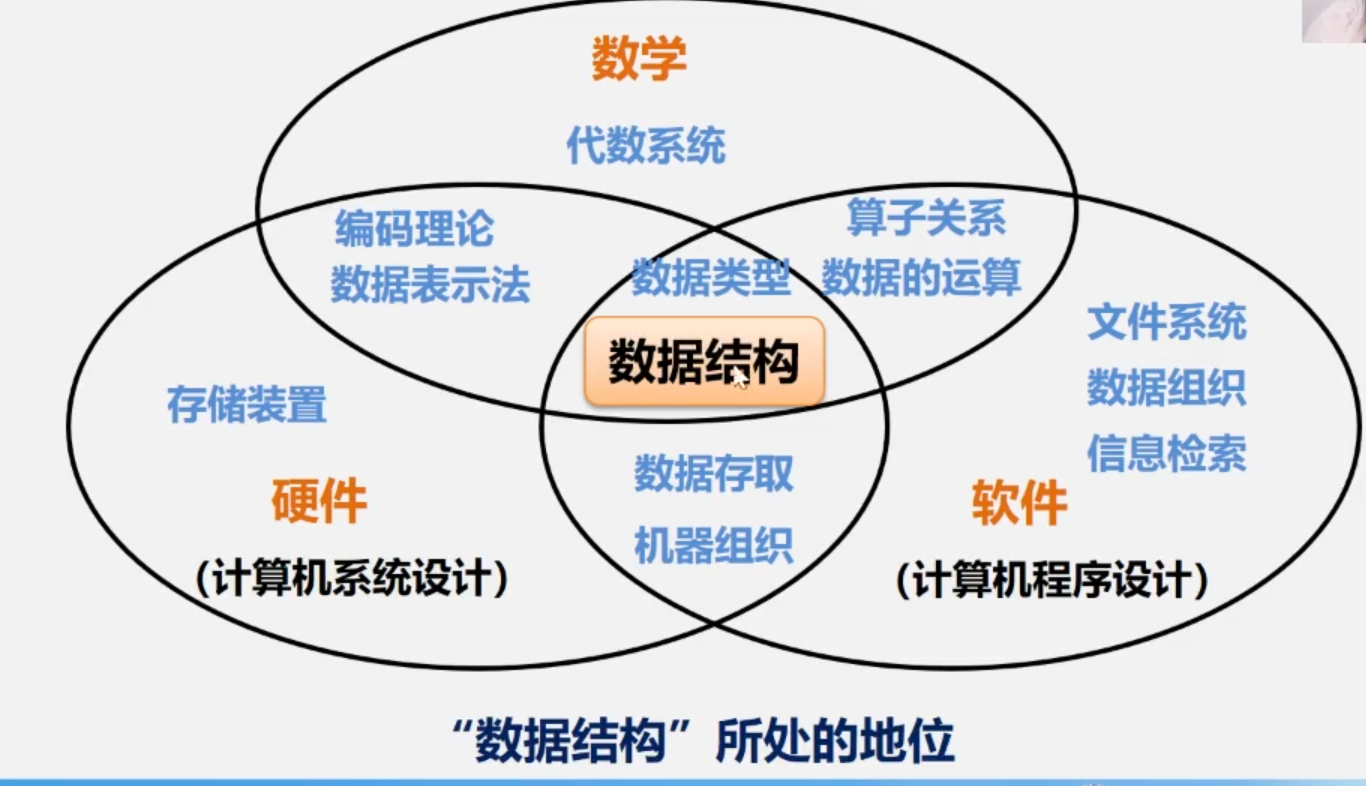
Chapter 1 basic concepts of data structure

Section I research content of data structure

Example 1 take the student management system as an example

Operation object: information of each student (student number, name, gender, native place, major, etc.)

Operation algorithm: query, insert, modify, delete

Relationship between operands: linear relationship. Data structure: linear data structure, linear table.

Example 2 man machine game problem

TicTacToe

Input the strategy into the computer and predict the development trend and even the final outcome of the chess game according to the current pattern.

Computer operation object: the state of various chess games

Computer algorithm: playing chess, deriving another pattern from one pattern.

Relationships between operands: nonlinear relationships, trees

Example 3: map navigation - find the shortest path

Operation object: information of each location and road

Computer algorithm: set up signal lights to find the set of each passable at the same time

Relationship between objects: nonlinear relationship, mesh structure

Section II basic concepts and terms

Data: a collection of symbols that can be input into and processed by a computer

• Carrier of information

• It is a symbolic representation of objective things

• It can be recognized, stored and processed by computer

include:

• Numeric data: integer, real number

• Non numerical data: text, image, graphics, sound.

Data element: the basic unit of data, which is usually considered and processed as a whole in computer programs.

Data item: the smallest indivisible unit that constitutes a data element.

Data object: a collection of data elements with the same properties and a subset of data.

Example:. 1 set of integer data objects N={0, ± 1, ± 2,...}

. 2 set of alphabetic data objects C = {'A', 'B',...}

. 3 the student status table can also be regarded as a data object

Data elements and data objects

Data element - the basic unit of data

Relationship with data: it is an individual of a collection

Data object - a collection of data elements of the same nature

The relationship with data is a subset of a set

Data structure:

Data elements do not exist in isolation. There is a certain relationship between them. The relationship between data elements is called structure.

A collection of data elements that have one or more specific relationships with each other.

In other words, a data structure is a collection of structured data elements.

Note: 1. The logical relationship between data elements is also called logical structure.

2. The representation of data elements and their relationships in computer memory (also known as image) is called the physical structure of data or the storage structure of data.

3. Data operation and implementation, that is, the operations that can be applied to data elements and the implementation of these operations on the corresponding storage structure.

Two levels of data structure:

Logical structure and physical structure

1. Logical structure:

(1) . describe the logical relationship between data elements

(2) It has nothing to do with the storage of data and is independent of the computer.

It is a mathematical model abstracted from specific problems.

2. Physical structure:

(1) The structure (storage mode) of data elements and their relationships in computer storage.

(2) . is the representation of data structure in computer.

Relationship between logical structure and storage structure:

1. Storage structure is the image of logical relationship and element.

2. Logical structure is the abstraction of data structure, and storage structure is the implementation of data structure.

Types of logical structures:

Division method I

(1) Linear structure

There is only one start and one end node, and all nodes have at most one direct precursor and one direct successor.

Example: linear table, stack, queue, string

(2) Nonlinear structure

A node may have multiple direct precursors and direct successors.

Example: tree and graph.

Division mode II - four basic logical structures

(1) Set structure: there is no relationship between data elements in the structure except that they belong to the same set.

(2) Linear structure: there is a one-to-one linear relationship between data elements in the structure.

(3) Tree structure: there is a one to many hierarchical relationship between data elements in the structure.

(4) Mesh structure: there is any many to many relationship between data elements in the structure.

Classification of storage structure:

Sequential storage structure, chain storage structure, index storage structure and hash storage structure.

(1) Sequential storage structure: a group of continuous storage units are used to store data elements in turn. The logical relationship between data elements is represented by the storage location of elements.

Note: C language uses array to realize sequential storage structure.

(2) Chained storage structure: a group of arbitrary storage units are used to store data elements, and the logical relationship between data elements is represented by pointers.

C language uses pointers to realize chain storage structure.

(3) Index storage structure: while storing node information, it also establishes additional index tables.

Each entry in the index table is called an index entry.

Keywords are those data items that can uniquely identify a node.

(4) Hash storage structure: directly calculate the storage address of the node according to the keyword of the node.

Section II basic concepts and terms (Continued)

1. When programming with high-level programming language, the data type of each variable, constant or expression in the program must be clearly stated.

Provide basic data types such as int, char, float, double, etc.

Array, structure, common body, enumeration, etc.

There are also pointer and void types

Users can also define their own data types with typedef

1.1 some of the most basic data structures can be implemented with data types, such as arrays, strings, etc

1.2 other commonly used data structures, such as stack, queue, tree, graph, etc., cannot be directly represented by data type.

2.1 data types in high-level languages clearly or implicitly specify all possible value ranges of variables and expressions during program execution, as well as the operations allowed on these value ranges.

For example, the variable i defined in C language is of type int, which is an integer representing the range [- mix,max]. Operations such as +, -, *, /,% can be performed on this integer set

Function of data type:

• Constrains the value range of a variable or constant,

• Operations that constrain variables or constants.

2. Data type

• Definition: data type is the general name of a set of values with the same nature and a set of operations on this set.
• Data type = value set + set of operations on value set.

2.1 abstract data type (ADT):

• It refers to a mathematical model and a set of operations defined on the mathematical model.

• It is defined by the user and abstracts the data model (logical structure) from the problem

• It also includes a set of abstract operations (related operations) defined on the data model

• Regardless of the specific storage structure in the computer and the specific implementation algorithm of operation

2.2 formal definition of abstract data types

2.3 the definition format of abstract data type is as follows:

ADT Abstract data type name{
    Data
        Definition of data object
        Definition of logical relationship between data elements
    Operation
        Operation 1
            initial condition 
            Operation result description
        Operation 2
            ......
        operation n
            ......
}ADT Abstract data type name

Basic operation definition format description:

• Parameter table: assignment parameters only provide input values for operations.
  • The reference parameter starts with & and returns the operation result in addition to the input value.

• Initial condition: describes the conditions that the data structure and parameters should meet before the operation is executed. If not, the operation will fail and the corresponding error message will be returned. If the initial condition is empty, it will be omitted

• Operation result: describes the change of data structure and the results to be returned after the operation is completed normally.

Section 3 representation and implementation of abstract data types

Abstract data type (ADT) definition example: Circle definition

ADT Circle{
    data object: D={r,x,y | r,x,y All are real numbers}
    Data relation: R={<r,x,y > | r Is the radius,<x,y>Is the center coordinate}
    basic operation :
    Circle(&C,r,x,y)
        Operation results: Construct a circle.
    double Area(C)
            initial condition : Circle already exists.
            Operation results: Calculate the area.
    double Circumference(C)
            initial condition : Circle already exists.
            Operation results: Calculate the perimeter.
        ......
}ADT Circle

The specific code implements Circle_1:

#include<stdio.h>

typedef struct circle{
float r;
float area;
float peri;
}*Circle;

float area(Circle c);
float peri(Circle c);

float area(Circle c){
c->area = 3.14*c->r*c->r;
return c->area;
}

float peri(Circle c){
c->peri= 2*3.14*c->r;
return c->peri;
}

void main(){
struct circle a;
printf("Please enter a radius: ");
scanf("%f",&a.r);
printf("The area of this circle is=%.2f\n",area(&a));
printf("The Perimeter of this circle is=%.2f\n",peri(&a));
}

The specific code implements Circle_2:

#include<stdio.h>
#include<assert.h>
#define PI 3.141592654

typedef struct Circle{
	float r;
	float x;
	float y;
}C;

void Circle(C* p){
	float n;
	printf("Please enter the radius:"); 
	scanf("%f",&n);
	p->r = n;
	p->x = 0;
	p->y = 0;
}

float Area(const C *p){
	assert(p != NULL);
	float ret = 0;
	float r = p->r;
	ret = PI*r*r;
	return ret;
}

float perimeter(const C *p){
	assert(p != NULL);
	float ret = 0;
	float r = p->r;
	ret = 2*PI*r;
	return ret;
}

int main(){

C c = {0};

Circle(&c);

float area = Area(&c);

float peri = perimeter(&c);

printf("The area of this circle is=%.2f\n",area);
printf("The Perimeter of this circle is=%.2f\n",peri);
return 0;
}

Abstract data type: complex implementation:

#include<stdio.h>
typedef struct
{
    float Realpart; //real part
    float Imagepart; //imaginary part
}Complex;
 
Complex Create(float x,float y)
{
    //Construct a complex number
    Complex C;
    C.Realpart=x;
    C.Imagepart=y;
    return C;
}
 
float GetReal(Complex C)
{
    //Take the real part of complex number C=x+yi
    return C.Realpart;
}
 
float GetImag(Complex C)
{
    //Take the imaginary part of complex number C=x+yi
    return C.Imagepart;
}
 
Complex Add(Complex C1,Complex C2)
{
    //Find the sum of two complex numbers C1 and C2
    Complex sum;
    sum.Realpart=C1.Realpart+C2.Realpart;
    sum.Imagepart=C1.Imagepart+C2.Imagepart;
    return sum;
}
 
Complex Sub(Complex C1,Complex C2)
{
    //Find the difference between two complex numbers C1 and C2
    Complex difference;
    difference.Realpart=C1.Realpart-C2.Realpart;
    difference.Imagepart=C1.Imagepart-C2.Imagepart;
    return difference;
}
 
int main ()
{
    float a,b,c,d;
    char e;
    Complex C1,C2,C3;
 
    //Enter a and b in the first group of complex numbers
    printf("Please enter plural C1 Real part and imaginary part of a and b((separated by spaces):");
    scanf("%f %f",&a,&b);
    C1=Create(a,b);
 
    //Enter c and d in the second set of complex numbers
    printf("Please enter plural C2 Real part and imaginary part of c and d((separated by spaces):");
    scanf("%f %f",&c,&d);
    C2=Create(c,d);
 
    //Add or subtract
    printf("Please select addition or subtraction(+/-):");
    getchar();
    scanf("%c",&e);
    if(e=='+')
        C3=Add(C1,C2);
    if(e=='-')
        C3=Sub(C1,C2);
 
    //Output results
    printf("The sum of two complex numbers/The difference is: %.2f+%.2fi",C3.Realpart,C3.Imagepart);
    return 0;
}
 

Section IV algorithm and algorithm analysis

Definition of algorithm:

A description of the methods and steps of solving a particular problem. It is a finite sequence of instructions. Each instruction represents one or more operations.

program = data structure＋algorithm
 Data structures are operated by algorithms
 The algorithm designs the program according to the data structure

1.4.1 characteristics of algorithm

1,Boundedness: an algorithm must always end after executing a finite step, and each step must be completed in a finite time./
2,Every instruction in deterministic algorithm must have exact meaning without ambiguity. Under any condition, there is only one execution path, that is, for the same input, only the same output can be obtained.
3,The feasibility algorithm is executable, and the operations described by the algorithm can be implemented by executing the basic operations that have been implemented for a limited number of times.
4,Input an algorithm has zero or more inputs/
5,output―An algorithm has one or more outputs.

1.4.2 basic criteria for algorithm design:

1. Correctness:

1,The program contains no syntax errors;
2,The program can get satisfactory results for several groups of input data;
3,The program can get satisfactory results for several groups of carefully selected, typical, harsh and difficult input data;
4,The program can get satisfactory results for the input data of - cut method.
Generally, the correctness of the third layer is used as the standard to measure whether an algorithm is qualified or not

2. Readability:

1,The algorithm is mainly for human reading and communication, followed by computer execution, so the algorithm should be easy to understand;
2,On the other hand, obscure and hard to read algorithms are easy to hide many errors and difficult to debug.

3. Robustness:

1,It means that when illegal data is input, the algorithm responds or processes appropriately, rather than producing inexplicable output results.
2,The method to deal with errors should not interrupt the execution of the program, but return a value representing the error or the nature of the error, so as to deal with it at a higher level of abstraction

4. Efficiency:

Requires minimal time and storage requirements

The efficiency of the algorithm is considered from the following two aspects:

1.Time efficiency:It refers to the time consumed by the algorithm;
2．Space efficiency:It refers to the storage space consumed in the execution of the algorithm.
Note: time efficiency and space efficiency are sometimes contradictory.

1.4.3 time complexity of algorithm:

1. Measurement of algorithm time efficiency:

The time efficiency of the algorithm can be measured by the time consumed by the execution of the program based on the algorithm on the computer.
Two measurement methods:

(1) Post statistics
The algorithm is implemented to calculate the space and space overhead.

·Disadvantages: it will take more time and energy to write a program to realize the algorithm; the experimental results depend on the computer software and hardware and other environmental factors, which mask the advantages and disadvantages of the algorithm itself
(2) Prior analysis:
An estimation method of the resources consumed by the algorithm.

• Algorithm running time = - time required for a simple operation × Number of simple operations
• That is, the sum of execution time of each statement in the algorithm is also called statement frequency
• Algorithm running time = execution times of each statement × The time required for the statement to execute once

For example, the algorithm for multiplying two n*n matrices can be described as:

for(i=1;i<=n;i++) 		//n+1 times
 
	for(j=1j<=n;j++){		// n(n+1) times

		c[i][j] == 0;       //n *n times

		for(k=0;k<n;k++)// n*n*(n+1) times
		    c[i][j]=c[i][jl+a[i][k]*b[k][j];// n*n*n times
		 }
                      
//We define the time consumed by the algorithm as the sum of the frequency of each statement in the algorithm, then the time consumption T(n) of the above algorithm is:
  //   T(n)=2n3＋ 3n2+ 2n +1

2. Time progressive complexity

If there is an auxiliary function f(n)，Make it right n When approaching infinity, T(h)/f(n)If the limit value of is a constant that is not equal to zero, it is called f(n)yes T(n)A function of the same order of magnitude T(n)=O(f(n))，call O(f(n))Is the asymptotic time complexity of the algorithm(ОIs an order of magnitude symbol)，Time complexity.

Example of square order:

×=O; y = 0;
for ( int k = 0; k < n; k++) 
 	x++;
for ( int i = o; i<n; i++ )
     for ( int j = 0;j < n; j++)
     	y++;

Cubic example:

x = 1;
for(i=1; i<n;i++)
     for(j=1;j<i;j++)
	     for(k=1;k<j;k++)
		     x++; 

Logarithmic order example:

i=1;         //(1)
while(i<=n)
i=i*2;       //(2)

If the cycle is executed once: i=1*2=2

If the cycle is executed twice:i=2*2=2^2

If the cycle is executed 3 times:i=2*2=2^3，
,
If loop execution x second: i=2^x
 Set statement②The number of executions is x Times, by cyclic conditions i< =n  
 -2x<=n :.x<=log2n

• Worst time complexity: refers to the time complexity of the algorithm in the worst case.
• Average time complexity: refers to the expected running time of the algorithm when all possible input instances occur with equal probability.
• Best time complexity: refers to the time complexity of the algorithm in the best case.

[the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-R6xyvFj6-1635853058576)(E: \. \ C.png)]

[the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-AeCEHwLW-1635853058578)(E: \. \ C.png)]

1.4.4 spatial complexity of algorithm

Space complexity: a measure of the storage space required by the algorithm,

Record as: S(n)=O(f(n))
Where n is the scale (or size) of the problem

//Algorithm 1
for(i=0;i<n/2;i++){
t = a[i];
a[i]=a[n-i-1];
a[n-i-1]=t; 
}
//Algorithm 2
for(i=0;i<n;i++)
	 b[i]=a[n-i-1];
for(i=0;i<n;i++)
     a[i]=b[i];

The space complexity of algorithm 1 is O(1)

Algorithm 2 space complexity O(n)

   //(2)

If the cycle is executed once: i=1*2=2

If the cycle is executed twice: i=2*2=2^2

If the cycle is executed 3 times: i=2*2=2^3,
,
If the cycle is executed x Times: i=2^x
Let the execution times of statement ② be x times, which is determined by the loop condition I < = n
-2x<=n :.x<=log2n

+ Worst time complexity:Refers to the time complexity of the algorithm in the worst case.
+ Average time complexity:It refers to the expected running time of the algorithm when all possible input instances occur with equal probability.
+ Best time complexity:Refers to the time complexity of the algorithm in the best case.

[External chain picture transfer...(img-R6xyvFj6-1635853058576)]



[External chain picture transfer...(img-AeCEHwLW-1635853058578)]



##### 1.4.4 spatial complexity of algorithm

Spatial complexity:A measure of the storage space required by the algorithm,

​         record as:S(n)=O(f(n))
among n Is the scale of the problem(Or size)

//Algorithm 1
for(i=0;i<n/2;i++){
t = a[i];
a[i]=a[n-i-1];
a[n-i-1]=t;
}
//Algorithm 2
for(i=0;i<n;i++)
b[i]=a[n-i-1];
for(i=0;i<n;i++)
a[i]=b[i];

The space complexity of algorithm 1 is O(1)

Algorithm 2 spatial complexity O(n)