1, Binary sort tree

1.1 definition of binary sort tree

Binary sort tree, also known as Binary Search Tree (BST), is a binary tree with the following properties:

• The keywords of all nodes on the left subtree are less than those of the root node;
• The keywords of all nodes on the right subtree are greater than those of the root node.
• The left subtree and the right subtree are each a binary sort tree;
• Left subtree node value < root node value < right subtree node value;
• Through the middle order traversal, you can get an increasing ordered sequence.
  

 // Binary sort tree storage structure
 typedef struct BSTNode{
    int key;
    struct BSTNode *lchild, *rchild;
}BSTNode, *BiTree;

1.2 searching binary sort tree

[analysis]: 1. If the tree is not empty, the value of k is compared with the root node. If it is equal, the search is successful; 2. k < root, search on the left subtree, otherwise search on the right subtree; 3. If the search is successful, the node pointer is returned; NULL if the lookup fails.

// Find the node with the value of key in the binary sort tree
BSTNode *BST_Sreach(BiTree T, int key){
    while(T!=NULL && key!=T->key){ //If the tree is empty or equal to the root node value, the loop ends
        if(key < T->key)
            T = T->lchild;  //If less than, search on the left subtree
        else
            T = T->rchild;  //If greater than, search on the right subtree
    }
    return T;
}
// Find the node with the value of key in the binary sort tree (recursive implementation)
BSTNode *BSTSreach(BiTree T, int key){ 
    if(T=NULL)
        return NULL;    // Search failed
    if(key=T->key)
        return T;       // Search succeeded
    else if(key < T->key)
        return BSTSreach(T->lchild, key);  //Look in the left subtree
    else
        return BSTSreach(T->rchild, key);  //Look in the right subtree
}

The worst space complexity O(h) required for recursive implementation of the two algorithms; Therefore, the first algorithm is better.

1.3 insertion of binary sort tree

[analysis]: 1. If the tree is empty, insert the node directly; 2. If the keyword k is less than the root node value, it is inserted into the left subtree; 3. If the keyword k is greater than the root node value, it is inserted into the right subtree.
The inserted node must be a newly added leaf node and the left child or right child of the last node accessed on the search path when the search fails.

// Insert a new node with keyword k into the binary sort tree (recursive implementation)
int BST_Insert(BiTree &T, int k){
    if(T=NULL){
        T = (BiTree)malloc(sizeof(BSTNode));
        T->key = k;
        T->lchild = T->rchild = NULL;
        return 1; //Returns 1. The insertion is successful
    }
    else if(k==T->key)
        return 0;
    else if(k<T->key)
        return BST_Insert(T->lchild,k);
    else
        return BST_Insert(T->rchild,k);
}

1.4 construction of binary sort tree

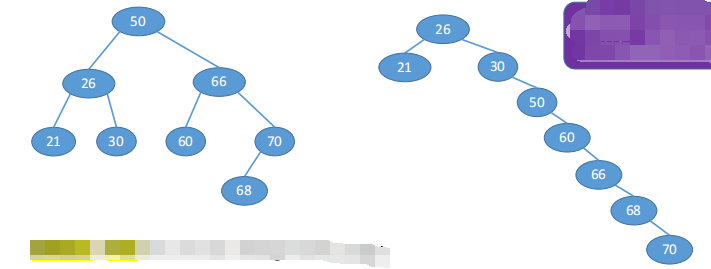
Starting from an empty tree, input the elements in turn and insert them into the appropriate position in the binary sort tree. If the keyword sequence to be searched is {45, 24, 53, 45, 12, 24}, the generated binary sort tree is shown in the figure.
[analysis]: start to make the tree empty, while cycle the insertion operation, and i count the total number of inserts

// Establish a binary sort tree according to the keyword sequence in str []
void Creat_BST(BSTree &T,int str[],int n){
    T=NULL;        //Initially, T is an empty tree
    int i=0;
    while(i<n){    // Insert each keyword into the binary sort tree in turn
        BST_Insert(T,str[i]); // Insert
        i++;
    }
}

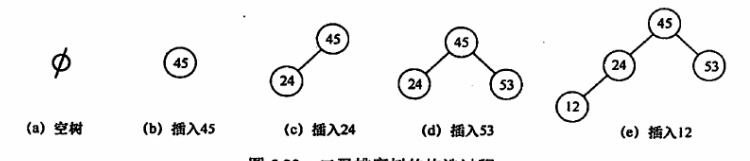
Different keyword sequences may get the same binary sort tree or different binary sort trees.

1.5 deleting binary sort tree

When deleting a node in a binary sort tree, you cannot delete all the nodes on the subtree with the node as the root. You must first remove the deleted node from the linked list storing the binary sort tree, and re link the binary linked list disconnected due to the deletion of the node, so as to ensure that the nature of the binary sort tree will not be lost. The implementation process of deletion is handled in three cases:

Search and find the target node first:

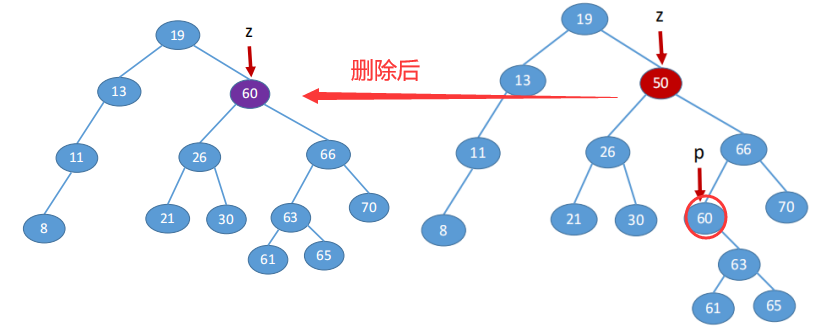
• ① If the deleted node z is a leaf node, it will be deleted directly, which will not destroy the nature of binary sort tree.
• ② If node z has only one left subtree or right subtree, let the subtree of z become the subtree of the parent node of z and replace the position of z.
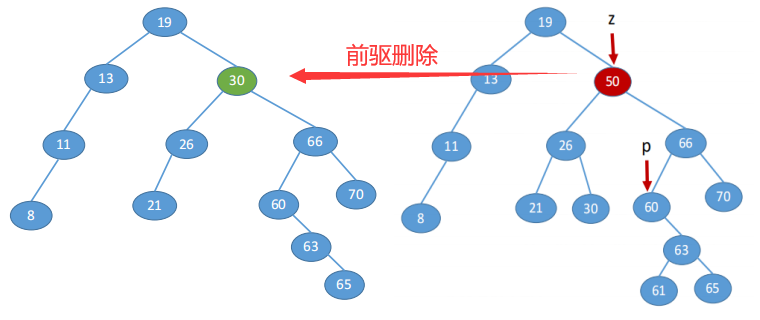
• ③ If node z has left and right subtrees, make the direct successor (or direct precursor) of z replace z, and then delete the direct successor (or direct precursor) from the binary sort tree, which is converted to the first or second case.

Successor of z: the leftmost lower node in the right subtree of z (the node must have no left subtree).

Precursor of z: the lowest right node in the left subtree of z (the node must have no right subtree)

1.6 search efficiency analysis

Search length - the number of times that keywords need to be compared in search operation is called search length, which reflects the time complexity of search operation.
The search efficiency of binary sort tree mainly depends on the height of the tree. If the absolute value of the height difference between the left and right subtrees of a binary sort tree does not exceed 1, such a binary sort tree is called a balanced binary tree, and its average search length is O(logn).

If the binary sort tree is a single branch tree with only right (left) children (similar to an ordered single linked list), its average search length is O(n). In the worst case, if the input sequence for constructing the binary sort tree is ordered, an inclined single branch tree will be formed. At this time, the performance of the binary sort tree will deteriorate significantly, and the height of the tree will increase to the number of elements n, as shown in the right figure.

Average Search Length ASL (Average Search Length)

chart(Left): ASL = (1*1 + 2*2 + 3*4 + 4*1)/8 = 2.625
 chart(right): ASL = (1*1 + 2*2 + 3*1 + 4*1 + 5*1 + 6*1+ 7*1)/8 = 3.75

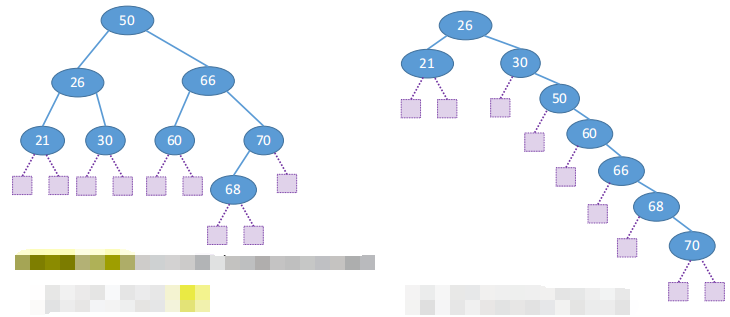
Average Search Length ASL (Average Search Length) of search failures

chart(Left): ASL = (3*7+4*2)/9 = 3.22 
chart(right): ASL = (2*3+3+4+5+6+7*2)/9 = 4.22