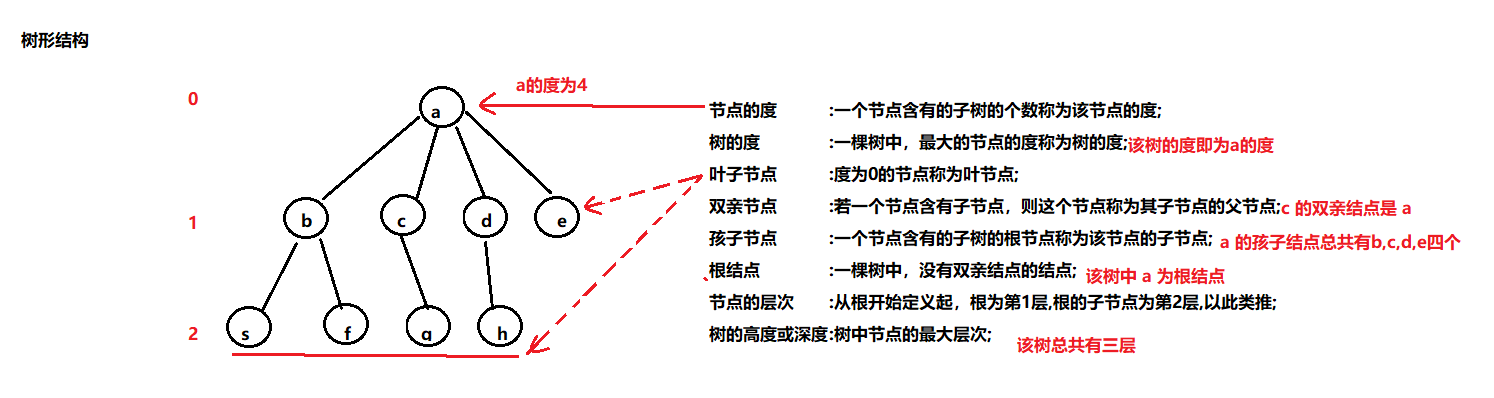
1. Tree structure: a tree is a finite set T of n (n > = 0) nodes. When n=0, it is called an empty tree; When n > 0, the set satisfies the following conditions:
(1) there must be a specific node called root, which has no direct precursor but 0 or more direct successors.
(2) the remaining n-1 nodes can be divided into m (M > = 0) disjoint finite sets, T1,T2,T3, ···· Tm, where Ti is a tree, called the subtree of the root. The definition of subtree is the same as that of tree.
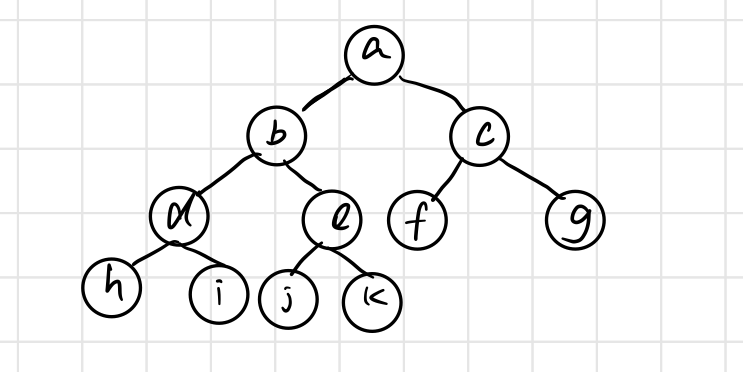
As shown in the figure:

* * some terms and related concepts about trees:

Degree of node: the number of subtrees contained in a node is called the degree of the node;
Tree degree: the degree of the largest node in a tree is called the degree of the tree;
Leaf node: a node with a degree of 0 is called a leaf node;
Parent node: if a node contains child nodes, this node is called the parent node of its child nodes;
The root of the node is called a child of the node;
Root node: a node in a tree without parent nodes;
Hierarchy of nodes: defined from the root, the root is the first layer, and the child nodes of the root are the second layer, and so on;
Height or depth of tree: the maximum level of nodes in the tree;

2. The binary tree meets the following conditions:
(1) the degree of each node shall not be greater than two;
(2) the order of each child can't be reversed.

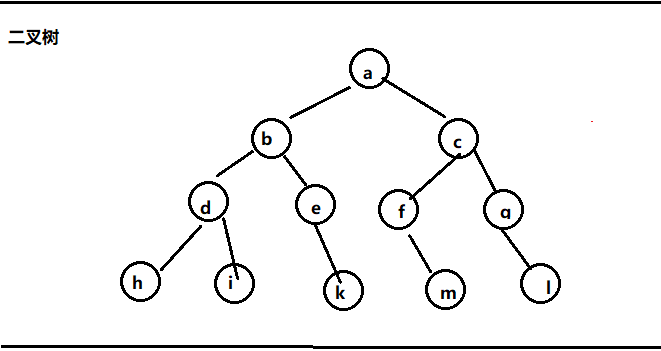
Two special binary trees:
    1. Full binary tree: a binary tree. If the number of nodes in each layer reaches the maximum, the binary tree is a full binary tree. That is, if
If the number of layers of a binary tree is K and the total number of nodes is 2k - 1, it is a full binary tree.

    2. Complete binary tree: a complete binary tree is a highly efficient data structure. A complete binary tree is derived from a full binary tree. For depth K, there is n
A binary tree with two nodes is called complete if and only if each node corresponds to the nodes numbered from 1 to n in the full binary tree with depth K
Binary tree. It should be noted that full binary tree is a special kind of complete binary tree.

 

 

Properties of binary tree:
    1. If the specified number of layers of the root node is 1, there are at most 2i-1 (I > 0) nodes on the i-th layer of - non empty = fork tree
    2. If the depth of the binary tree with only the root node is specified as 1, the maximum number of nodes of the binary tree with depth K is 2K - 1 (k > = 0)
    3. For any - tree = = fork tree, if the number of leaf nodes is n0 and the number of non leaf nodes with degree 2 is n2, there is n0= n2 + 1
    4. The depth k of a complete binary tree with n nodes is rounded on log2(n + 1)
    5. For a complete binary tree with n nodes, if all nodes are numbered from 0 from top to bottom and from left to right, the sequence number is i
The nodes are:
If I > 0, parental serial number: (i-1)/2; i=0, i is the root node number, no parent node.
If 2i+1 < n, left child serial number: 2i+1, otherwise there is no left child
If 2i+2 < n, right child serial number: 2i+2, otherwise there is no right child

Binary tree code implementation:
Node class:

public class Node <E extends Object> {
    public E val;
    public Node<E> left;   // Left child
    public Node<E> right;   // Right child
    public Node(E val){
        this.val=val;
    }
}

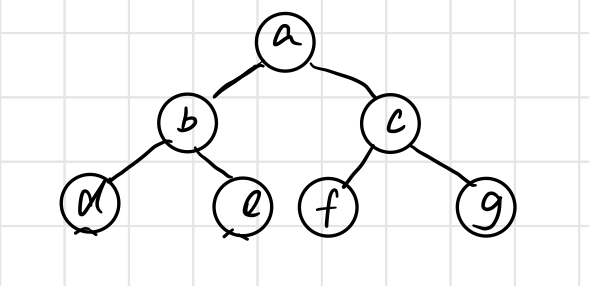
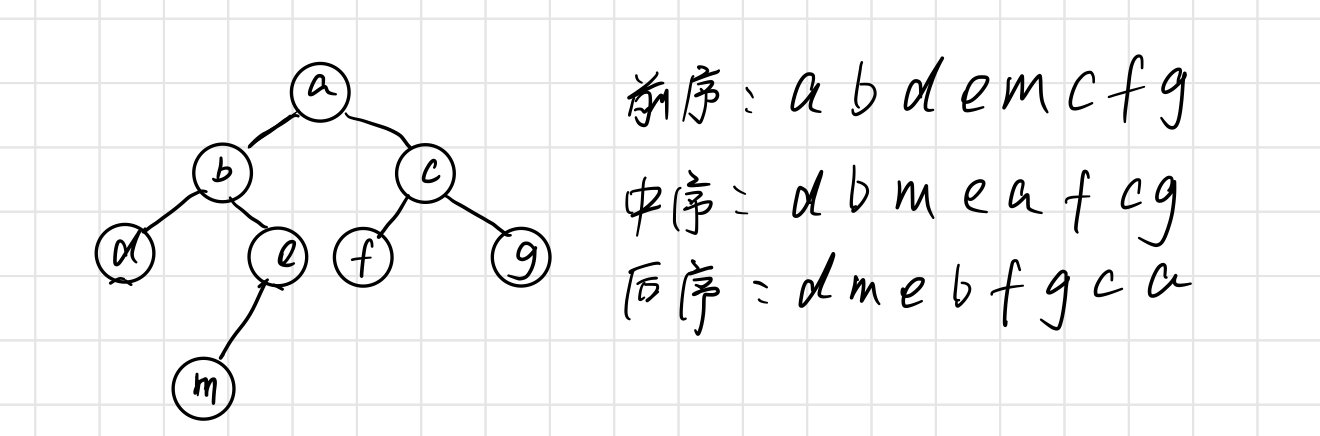
For the basic operation of binary tree, take the following binary tree as an example:

 //Build tree
    public static Node<Character> BuildTree(){
        Node<Character> n1 = new Node<>('a');
        Node<Character> n2 = new Node<>('b');
        Node<Character> n3 = new Node<>('c');
        Node<Character> n4 = new Node<>('d');
        Node<Character> n5 = new Node<>('e');
        Node<Character> n6 = new Node<>('f');
        Node<Character> n7 = new Node<>('g');
        Node<Character> n8 = new Node<>('m');
        n1.left = n2;n1.right = n3;
        n2.left = n4;n2.right = n5;
        n3.left = n6;n3.right = n7;
        n5.left = n8;
        return n1;
    }

  

1. Recursively traversing binary tree:
(1) root, left and right (previous sequence): abdemcfg

//Preorder traversal
    public static void preOrder(Node<Character> root){

        if (root != null){
            //If the certificate is empty, do nothing and exit.
            System.out.print(root.val);//Print the value of the current node.
            preOrder(root.left);//The pre order traverses the left subtree and decomposes the problem into small problems.
            preOrder(root.right);//Preorder traversal right subtree
        }
    }

The operation result is:

(2) left, root and right (middle order): dbmeafcg

//Middle order traversal
    public static void inOrder(Node<Character> root){

        if (root != null){
            //If the certificate is empty, do nothing and exit.
            inOrder(root.left);//Traverse the left subtree in middle order and decompose the problem into small problems.
            System.out.print(root.val);//Print the value of the current node.
            inOrder(root.right);//Middle order traversal right subtree
        }
    }

The operation result is:

(3) left, right and root (later order): dmebfgca

//Postorder traversal
    public static void postOrder(Node<Character> root){

        if (root != null){
            //If the certificate is empty, do nothing and exit.
            postOrder(root.left);//After traversing the left subtree, the problem is decomposed into small problems.
            postOrder(root.right);//Postorder traversal right subtree
            System.out.print(root.val);//Print the value of the current node.
        }
    }

Operation results:

Summary: when traversing a binary tree, you can see that recursion is a good choice. When we get a binary tree, we first split it into:
The structural form of left subtree + root node + right subtree. Then do the same operation for its "left subtree" and "right subtree", that is, recursion.
As for the order, it is consistent with the traversal order you choose. For example, the previous order is: root node + left subtree + right subtree.

Sequence traversal binary tree: the principle is relatively simple, that is, traversing the binary tree from top to bottom and from left to right.

//level traversal 
    public static void levelOrder(Node<Character> root){
        //We will not put null values in the queue from the beginning.
        Queue<Node<Character>> queue = new LinkedList<>();
        if (root != null){
            queue.offer(root);
        }
        //If the queue is not empty, it proves that it has not been traversed.
        while ( !queue.isEmpty() ){
            Node<Character> node = queue.poll();
            //Access current node value
            System.out.print(node.val);
            if (node.left != null){
            //If there is a left child, let the left child join the team
                queue.offer(node.left);
            }
            if (node.right != null){
            //If there is a right child, let the right child join the team
                queue.offer(node.right);
            }
        }
    }

Conclusion: sequence traversal must be related to queue, so we must think of queue when referring to sequence traversal. When traversing layer i, all nodes of this layer must be
Go through it all. Sometimes the topic will require all nodes to be classified by level. At this time, it is necessary to record the level of nodes while traversing the sequence.

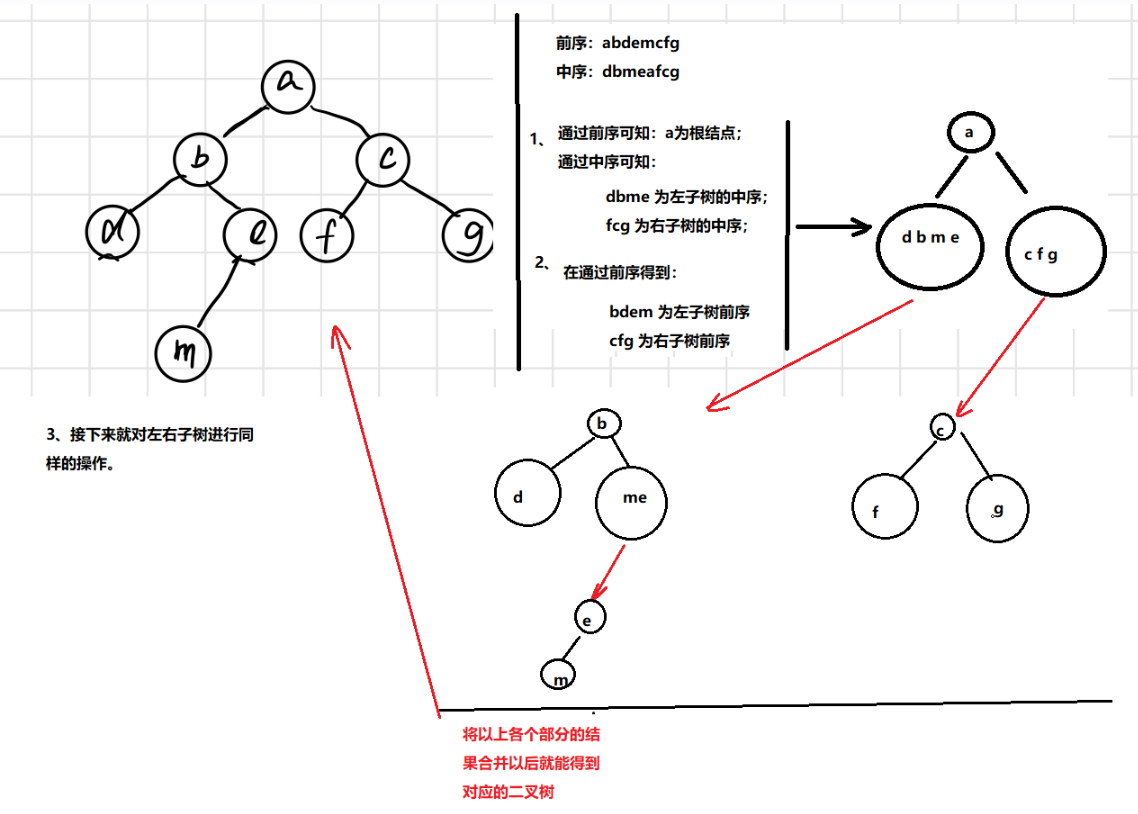
**Given a tree, we can get the first, middle and last traversal order. Suppose given a certain order, can you draw a tree?
If only one order is given, the specific structure of input cannot be determined.
However, the two cases of pre order + middle order or post order + middle order are acceptable.
Discussion preface + middle Preface:
1. Find the root node (the first element of the preamble) in the preamble.
2. Find the middle order of the left subtree and the right subtree in the middle order.
The middle order sequence of the left subtree: the front part of the root node.
The middle order sequence of the right subtree: the later part of the root node.
3. Find the pre order of the left and right subtrees in the pre order
Left subtree pre order: starting from the next position of the root node, the length is the length of the order sequence in the left subtree.
Right subtree preamble: after finding the preamble sequence of the left subtree, the rest is the preamble sequence of the right subtree.
We consider the construction process of pre order and middle order, which is a recursive process, so after we get the pre order and middle order of left subtree and right subtree,
Using the decomposition method similar to left subtree + root node + right subtree, continue to operate the left subtree and right subtree in steps 1, 2 and 3.