[data structure] Bloom Filter of initial data structure and its implementation
If you think it's helpful to you, can you point a praise or close a note to encourage the author?! Blog directory | click here first
- Premise concept
- What is a bloom filter?
- What is the function of Bloom filter?
- Defects of Bloom filter
- data structure
- Key factors
- Structural design
- code implementation
- structural morphology
- Factor calculation
- hash function
- Insert element
- Does it exist
- problem
- How much space can bloom filter save?
Premise concept
What is a bloom filter?
Bloom Filter (English: Bloom Filter) was proposed by bloom in 1970. It is actually a very long binary vector and a series of random mapping functions. Bloom Filter can be used to retrieve whether an element is in a set. Its advantage is that its spatial efficiency and query time are far higher than those of general algorithms, but its disadvantage is that it has a certain false recognition rate and deletion difficulty
What is the function of Bloom filter?
What is the function of Bloom filter? Generally speaking, the main function of Bloom filter is to "retrieve whether an element exists in it with lower spatial efficiency"
Therefore, we know that the advantage of Bloom filter is to save space, and its function is to judge whether an element exists. Combined with the actual application scenarios, what are the application scenarios of Bloom filter?
- It is recommended to remove re filtration
- For example, for a short video recommendation system, in the video feed stream scene, the requirement is that after recommending the specified content to the user, the recommended content will not appear again for a period of time, so the bloom filter can be of great use.
- Cache penetration filtering
- For example, in the Internet large concurrency scenario, in order to prevent large-scale traffic penetration from crushing RDS, many systems will use cache to resist traffic. Therefore, we can also consider using Bloom filter to record the identified external illegal requests or empty result requests in the filter, and filter them in advance in the next visit
- Blacklist system
- For example, some systems need to record millions, tens of millions or even more blacklist characters. Using the traditional hash table requires a large storage space. Then we can also use bloom filter to provide the same ability and effectively reduce the storage cost
Disadvantages of Bloom filter
We all know that bloom filter has the advantage of saving space and storage cost compared with the traditional container of "whether the retrieval element exists", especially in the field of big data. So it has only advantages and no defects?
No, the bloom filter also has two very important defects
- The false positive rate is fpp
- Does not have the ability to delete elements
What does it mean to have a certain misjudgment rate? It means that "non-existent elements may be misjudged as existence", and this probability is fpp. How to avoid and solve it?
- Firstly, there must be misjudgment. If the misjudgment cannot be accepted, the bloom filter is not suitable for use. However, we can reduce the probability according to business needs, or select the probability of misjudgment acceptable to us;
- The false positive rate (false positive rate) is affected by the number of hash functions, the size of bit groups, and the number of expected elements
- Generally, acceptable fpp is selected to build bloom filter according to business requirements, such as fpp = 0.001, misjudgment once every 1000 times
In addition, what does it mean that you don't have the ability to delete elements? According to the design of Bloom filter, an element will be calculated by multiple hash functions and get multiple different positions; Because the implementation is based on hash, there must be hash conflict, that is, the hash values of some hash functions of multiple elements may be consistent, that is, multiple elements will share some locations. If we want to delete an element, we need to reset its position to 0, but this may affect the judgment of other elements sharing the position. Therefore, to sum up, the bloom filter does not support deletion. If you want to delete it, how do you solve it?
The bloom filter cannot be solved, but it can be extended based on the bloom filter to derive removable filters, such as CBF (counting bloom filter) and Cuckoo Filter. If you want to delete, the basic configuration of the bloom filter is insufficient, and other similar data structures can be used
data structure
Key factors
- bloom filter calculate
- n is the number of elements expected to be supported by the filter
- m is the size of the filter bit group, that is, how many bits of space the filter occupies in total
- c is the average space occupied by each element
- p is the false positive probability, i.e. fpp (false positive probability)
- Number of k hash functions
Calculation formula
- m = -nlogp/(log2)^2
- c = m/n
- p = (1-[1-1/m]^kn)^k ~= (1-e^(-kn/m))^k = (1-e^(-k/(m/n))^k = (1-e^(-k/c))^k
- k = m/n * ln2 = 0.7m/n

Usually, to create a bloom filter, you need to provide the n you want to support and the expected p, and then get the rest of the best parameters through the formula
Structural design
The data structure of Bloom filter is actually quite simple. If you have known bitmap before, it will be even simpler. The bottom implementation of the whole bloom filter is based on "bit group + hash function"
Suppose that the bit group size of a bloom filter is 1000 bits, that is, 1000 bits. It consists of three hash functions
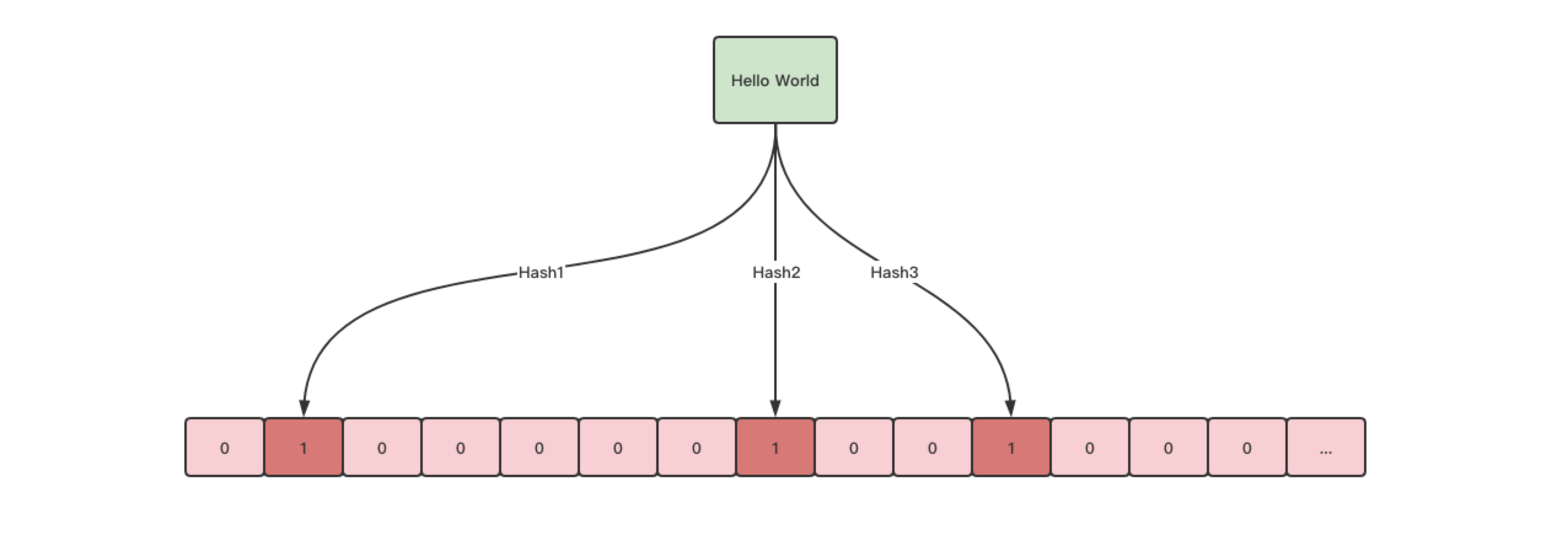
When we pass an element (Hello World) into the bloom filter, the element will be calculated through three hash functions to obtain three hash values. Finally, the hash value is mapped to the specific x bit of the bit group through modular operation and marked as 1
When we want to judge whether an element is in the bloom filter, similarly, we also pass in the element, calculate it through the hash function, and obtain the index value of the mapped bit group to judge whether the bits of these indexes are 1. If they are all 1, it means that the element already exists, but as long as one position is not 1, we think that the element does not exist
code implementation
structural morphology
The structure of Bloom filter can be mainly composed of three parts: key factor (n,m,p,k...), hash function and digit group. Therefore, if we want to implement a bloom filter, we must first build the above three parts. Here is a pseudo code, which can basically reflect the structural design of Bloom filter
public abstract class BloomFilter {
// Byte array
byte[] bytes;
// Key factors
int n;
double p;
int m;
int k;
// hash function
List<Hash> hashes;
// Insert element
public void put(byte[] bs);
// Does it exist
public boolean contains(byte[] bs);
}
- Why N and m are int instead of long? Because there is no concept of bit group in Java, we use byte array to realize bit group, and the maximum size of array is integer MAX_ Value, so n,m also use int
- In fact, it is not without the concept of bit group. It can be implemented through the BitSet provided by Java, which will be simpler. However, the purpose here is to learn, so we don't use wheels directly. In addition, there are many practices that use long arrays
Factor calculation
- The best m is calculated by (n,p)
/**
* Computes m (total bits of Bloom filter)
*/
public static int optimalNumOfBits(int n, double p) {
if (p == 0) {
p = Double.MIN_VALUE;
}
return (int) (-n * Math.log(p) / (Math.log(2) * Math.log(2)));
}
- The best k is calculated by (n,m)
/**
* Computes the optimal k
*/
public static int optimalNumOfHashFunctions(int n, int m) {
// (m / n) * log(2), but avoid truncation due to division!
return Math.max(1, (int) Math.round((double) m / n * Math.log(2)));
}
- The best p is calculated by (n,m,k)
/**
* Computes the false positive probability
* 1. p = (1 - e ^ (-kn/m))^k
*/
public static double optimalFpp(int n, int m, int k) {
// keep 5 digits after the decimal point
int point = 100000;
return (double) Math.round((point * Math.pow(1 - Math.exp((double) (-k * n) / m), k))) / point;
}
- c is calculated by (n,m)
/**
* Bits occupied each element
*/
public static double bitsOfElement(int n, int m) {
return (double) m / n;
}
- Usually, we can construct an expected bloom filter through n and p passed by the user
hash function
Hash functions can be matched with various hybrid hash algorithms. For simple implementation, I suggest murmur3 hash to achieve different hash effects by adding different seed salts
// Member variable k hash functions
private List<Hash> hashes;
// Get k index values
public int[] hashes(byte[] bs) {
int[] indexs = new int[hashes.size()];
for (int i = 0; i < hashes.size(); i++) {
//
int index = (int) ((hashes.get(i).hashToLong(bs) & Long.MAX_VALUE) % this.m);
indexs[i] = index;
}
return indexs;
}
// Hash interface
public interface Hash {
long hashToLong(byte[] bs);
}
Here is the pseudo code. The Hash interface is not implemented. murmur3 salt can be used to implement multiple Hash functions
- hashToLong is the incoming data to obtain a 64 bit hash value
- Why & long MAX_ What about value? The purpose is to make the hash value a positive number (when compared with 01111... It is naturally a positive number)
- Why% m is the total number of bits of Bloom filter, and the position in the filter is obtained through the hash value
Insert element
// Insert element & does it exist
public synchronized void put(byte[] bs) {
int[] indexs = hashes(bs);
for (int index : indexs) {
// The specific byte in which the
byte bits = (byte) (index / B);
// Specific bit
byte offset = (byte) (1 << (B_MASK - (index % B)));
bytes[index / B] = (byte) (bits | offset);
}
}
- B = 8, representing 8 bits of a byte; B_MASK is a mask, B_MASK = B - 1, for modulo operation
- First, get the index, and get the byte where the index is located through index / B
- Secondly, get the specific bit index of the byte through index% B, for example, it is equal to 2, (00100000, a byte has 8 bits, and the position of 1 is 2)
- After knowing the specific bit index through index% B, in order to change the position to 1, we need to get the offset of bit addition, that is, get 00100000 to add
- How did you get that? That is, move 00000001 left B_ Mask - (index% B) = 7 - 2 = 5 bits. After moving 5 bits left, 00100000 is obtained
- Assuming that the byte is 10000001 and we want to change the position with index 2 to 1, we can do or operation on two bytes, that is, bit addition, 10000001 | 00100000 = 10100001
- Finally, you can overwrite the bit of index
Does it exist
// Does it exist
public synchronized boolean contains(byte[] bs) {
int[] indexs = hashes(bs);
for (int index : indexs) {
byte bits = (byte) (index / B);
byte offset = (byte) (1 << (B_MASK - (index % B)));
if ((bits & offset) == 0) {
return false;
}
}
return true;
}
- Whether there is a bit operation principle is consistent with the inserted element. Just look at the insertion directly
- It should be distinguished because there are multiple hash functions, naturally there are multiple indexes. As long as one index is not 1, we think it does not exist
Pseudo code framework
In fact, it is not difficult to implement a complete bloom filter. I attach a simplified bloom filter pseudo code here. Basically, except for the selection of hash function, other logic has basic implementation, which can be used for simple reference, understanding and learning
/**
* @author SnailMann
*/
public abstract class BloomFilter {
// A byte has 8 bits
private static final int B = 8;
// B mask
private static final int B_MASK = B - 1;
// Byte array
private byte[] bytes;
// Key factors
private int n;
private int p;
private int m;
private int k;
List<Hash> hashes;
public BloomFilter(int n, int p) {
this.n = n;
this.p = p;
this.m = optimalNumOfBits(n, p);
this.k = optimalNumOfHashFunctions(this.n, this.m);
this.bytes = new byte[this.m];
}
// Insert element & does it exist
public synchronized void put(byte[] bs) {
int[] indexs = hashes(bs);
for (int index : indexs) {
// The specific byte in which the
byte bits = (byte) (index / B);
// Specific bit
byte offset = (byte) (1 << (B_MASK - (index % B)));
bytes[index / B] = (byte) (bits | offset);
}
}
public synchronized boolean contains(byte[] bs) {
int[] indexs = hashes(bs);
for (int index : indexs) {
byte bits = (byte) (index / B);
byte offset = (byte) (1 << (B_MASK - (index % B)));
if ((bits & offset) == 0) {
return false;
}
}
return true;
}
public int[] hashes(byte[] bs) {
int[] indexs = new int[hashes.size()];
for (int i = 0; i < hashes.size(); i++) {
int index = (int) ((hashes.get(i).hashToLong(bs) & Long.MAX_VALUE) % this.m);
indexs[i] = index;
}
return indexs;
}
private static int optimalNumOfHashFunctions(int n, int m) {
return Math.max(1, (int) Math.round((double) m / n * Math.log(2)));
}
private static int optimalNumOfBits(int n, double p) {
if (p == 0) {
p = Double.MIN_VALUE;
}
return (int) (-n * Math.log(p) / (Math.log(2) * Math.log(2)));
}
public interface Hash {
long hashToLong(byte[] bs);
}
}
If you need a complete and available implementation, you can refer to the relatively complete code implemented by the blogger before
problem
How much space can bloom filter save?
We all know that bloom filter can greatly save space, so how much space can it save** How to calculate this** After we learned the calculation of key factors, this is simply a small thing
We know that c = m/n, and c represents the average space occupied by each element in the bloom Filter, that is, how many bits. We assume to construct a Filter that satisfies the conditions of P = 0.001 and N = 10000

After calculation, we can know that M = 143776 and K = 10, then the average space occupied by each element is c = m/n = 14.38 bits. Usually, the type of primary key will be 32 / 64 integer or string
- Suppose that the element we want to judge is a 64 bit integer, and a 64 bit value accounts for 64 bits, so we compress nearly (64-14.38 / 64) = 63% of the space for each element
- Assuming that the element we want to judge is a 32 length string, and each string occupies 32 * 8 = 256 bits, we compress nearly 94% of the space for each element
This is the calculation method of single element space compression. If it is not intuitive enough, we can calculate it according to the total amount. Assuming n = 100000000 (100 million), p = 0.001 and c = 14.38, then m will be 1437758757 bits (171.39MB). Assuming that it is still a 32 length string, to store 100 million such characters, we need a space size of 256 * 100000000 = 25600000000 = 2.98 GB, while if we use bloom filter, we only need 171 MB
If you think this space compression is nothing more than this, then enlarge the amount of data and increase it by 10000 times. Can you smell it 💰 What's the smell of? Isn't it fragrant to save costs and give a year-end bonus?
reference material
- If you think it's helpful to you, can you point a praise or close a note to encourage the author?!
- Bloom filter supporting LRU - @ SnailMann