1. Definitions and basic terms of drawings
①. Definition of graph
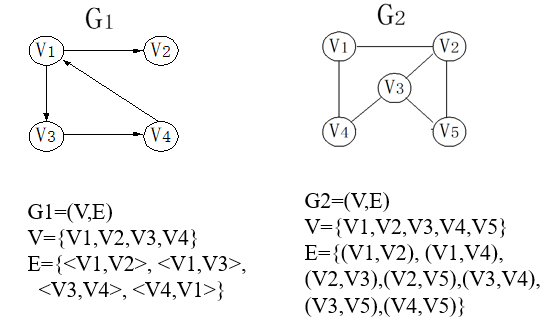
Graph G is composed of two sets V and E, marked as G=(V,E), where V is the finite nonempty set of vertices, e is the finite set of vertex pairs in V, and these vertex pairs are symmetrical as edges. V(G) and E(G) usually represent the vertex set and edge set of graph G respectively, and E(G) can be an empty set. If E(G) is empty, graph G has only vertices and no edges.
Directed graph:
Each edge has a direction, and the edge is also called an arc, such as G1
Undirected graph:
Each edge is undirected, such as G2
②. Basic terms of Graphs
Let n represent the number of vertices in the graph and e represent the number of edges
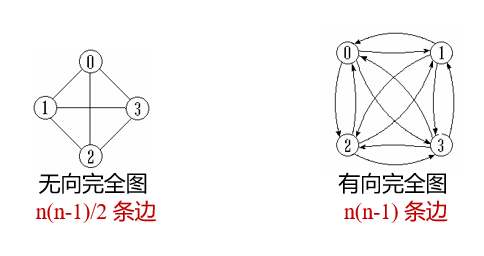
Complete graph: any two points have an edge connected
Sparse graph: if the number of edges or arcs satisfies e < n log2n, it is called sparse graph, otherwise it is called dense graph
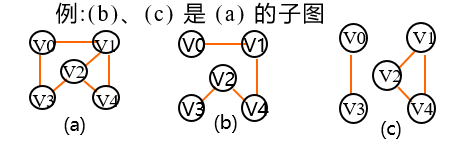
Subgraph: there are two graphs G=(V, {e}) and G1= (V1, {E1}). If V1 ⊆ V and E1 ⊆ e, G1 is said to be the subgraph of G.
Weight and net: the number of edges or arcs in a graph is called weight. Indicates the distance or cost from one vertex to another. A weighted graph is called a net.
For undirected graphs:
Adjacency point: if there is an edge a between vertex v and vertex w, vertices V and w are called adjacency points. Edge a is associated with vertices V and w.
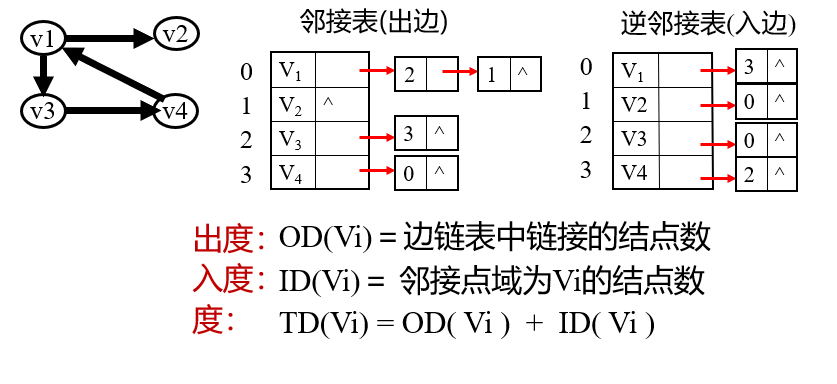
Degree: the number of edges associated with vertex v, recorded as TD(v)
For a directed graph:
< x, Y > is a directed edge (ARC),
x is the starting point (arc tail) of the directed edge, and y is the ending point (arc head) of the directed edge
The penetration of vertex v is the number of directed edges ending at V, which is recorded as ID(v)
The outgoing degree of vertex v is the number of directed edges with V as the starting point, which is recorded as OD(v)
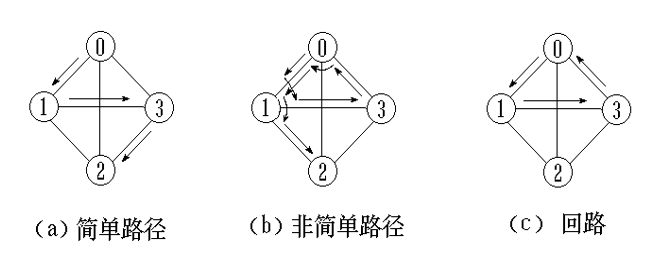
Path: a sequence of vertices formed by successive edges.
Path length: the number of edges or arcs on the path.
Simple path: a path with different vertices except that the start and end points of the path can be the same.
Simple loop (simple loop): a path with different vertices except for the same start and end points
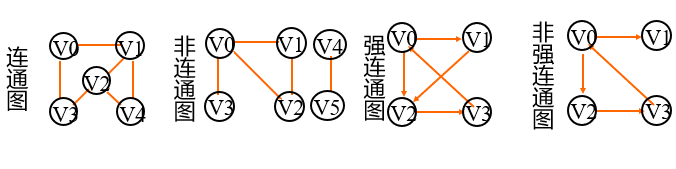
If any two vertices in an undirected graph have paths connected, the graph is called connected graph (G1); If an undirected graph is a non connected graph, each connected subgraph in the graph is called the connected component (G2) of the graph.
If there is a directed path between any two vertices in a directed graph, it is called a strongly connected graph. Otherwise, its strongly connected subgraphs are called its strongly connected components.
2. Type definition of graph
Abstract data type definition of diagram:


3. Storage structure of graph
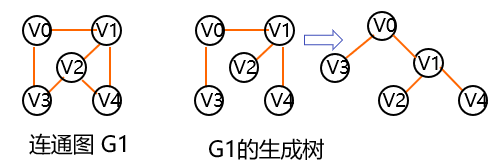
Due to the complex structure of the graph, there may be a connection between any two vertices, so the relationship between elements cannot be expressed by the physical position of data elements in the storage area, that is, the graph has no sequential storage structure, but the relationship between elements can be expressed by means of two-dimensional array, that is, adjacency matrix representation. On the other hand, because there may be a relationship between any two vertices of a graph, it is natural to use chain storage to represent a graph. There are many kinds of chain storage of graphs, including adjacency list, cross linked list and adjacency multiple list. Different storage structures should be selected according to different actual needs.
①. adjacency matrix
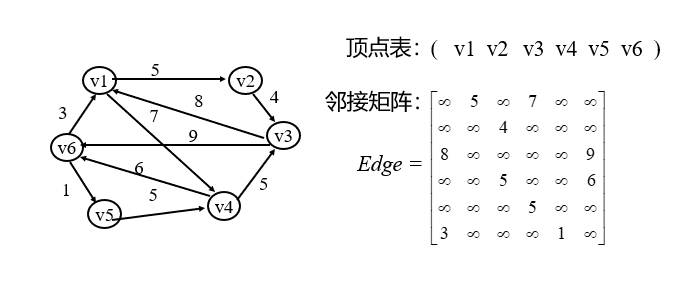
adjacency matrix
Adjacency matrix is a matrix that represents the adjacency relationship between vertices. Let g (V, E) be a graph with n vertices, then the adjacency matrix of G is an n-order square matrix with the following properties.

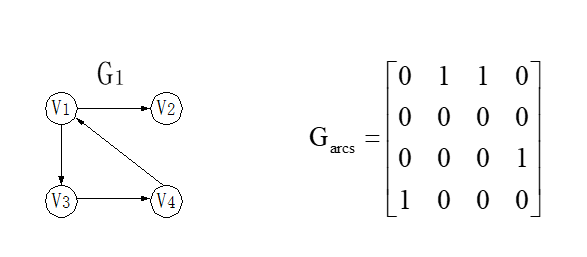
In the adjacency matrix of a directed graph,
- Meaning of line I: node v; Is the edge of the starting point (i.e. the exit edge);
- Meaning of column I: node v; Is the edge of the end point (i.e. in degree edge).
The adjacency matrix of a directed graph may be asymmetric.
- Vertex out - sum of elements in line i
- Vertex penetration - sum of elements in column i
- Degree of vertex - sum of elements in row i + sum of elements in column i
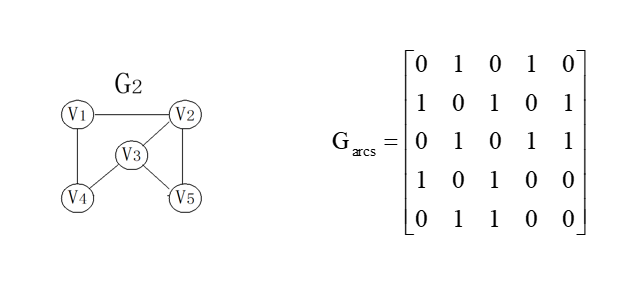
The adjacency matrix of an undirected graph is symmetric;
- Degree of vertex i = number of 1 in row I (column);
- The number of edges of the graph = half of the sum of all non-0 elements;
- In the adjacency matrix of a complete graph, the diagonal elements are 0 and the rest are 1.
If G is a net, the adjacency matrix can be defined as:
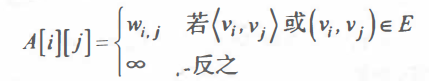
Where, WI and j represent the weight on the edge; ∞ represents the number allowed by the computer and greater than the weight on all edges.
Characteristics of adjacency matrix representation
- Advantages: it is easy to realize the operation of the diagram.
For example: find the degree of a vertex, judge whether there are edges between vertices, find the adjacent points of vertices - Disadvantages: n vertices require n*n cells to store edges; The spatial efficiency is O(n2).
It is especially a waste of space for sparse graphs.
//Storage representation of adjacency matrix of graph
#define MaxInt 32767 / / indicates the maximum value, i.e. ∞
#define MVNum 100 / / maximum number of vertices
typedef char VerTexType; //Assume that the data type of the vertex is character type
typedef int ArcType; //It is assumed that the weight type of the edge is integer
typedef struct
{
VerTexType vexs[MVNum]; //Vertex table
ArcType arcs[MVNum][MVNum]; //adjacency matrix
int vexnum, arcnum; //The current number of vertices and edges of a graph
} AMGraph;
Using adjacency matrix representation to create undirected network
- Enter the total number of vertices and edges.
- Input the information of points in turn and store it in the vertex table.
- Initialize the adjacency matrix so that each weight is initialized to a maximum value.
- Construct adjacency matrix. Input the vertex attached to each edge and its weight in turn. After determining the position of the two vertices in the graph, make the corresponding edge give corresponding weight, and make its symmetrical edge give the same weight.
Status CreateUDN(AMGraph &G)
{ //The adjacency matrix representation is used to create undirected network G
cin >> G.vexnum >> G.arcnum; //Enter the total number of vertices and edges
for (i = 0; i < G.vexnum; ++i)
cin >> G.vexs[i]; //Enter the information of the points in turn
for (i = 0; i < G.vexnum; ++i) //Initialize the adjacency matrix, and set the weights of the edges to the maximum
for (j = 0; j < G.vexnum; ++j)
G.arcs[i][j] = MaxInt;
for (k = 0; k < G.arcnum; ++k) //Construct adjacency matrix
{
cin >> v1 >> v2 >> w; //Enter the vertex and weight of an edge
i = LocateVex(G, v1);
j = LocateVex(G, v2); //Determine the position of v1 and v2 in G
G.arcs[i][j] = w; //The weight of edge < V1, V2 > is set to w
G.arcs[j][i] = G.arcs[i][j]; //Set the weight of the symmetrical edge < V2, V1 > of < V1, V2 > to w
} // for
return OK;
} // CreateUDN
The time complexity of the algorithm is O(n2).
If the weight of the above algorithm is 0, it is only necessary to initialize two adjacent edges; Second, when constructing the adjacency matrix, change the weight w to a constant value of 1. Similarly, a directed network or graph can be established by slightly modifying the algorithm.
②. Adjacency table
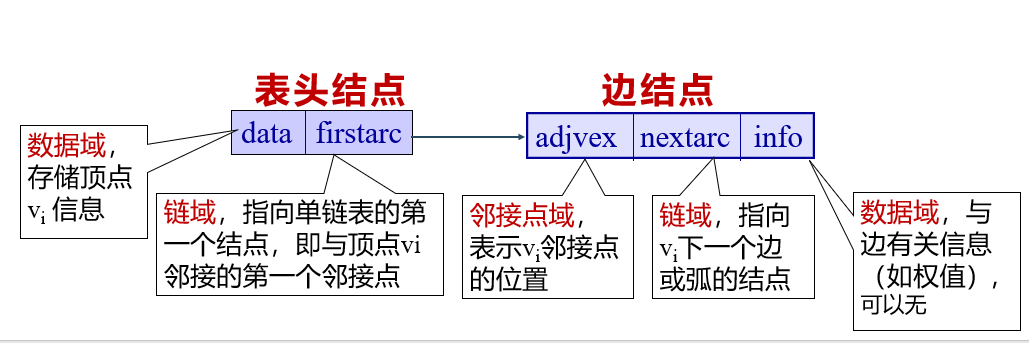
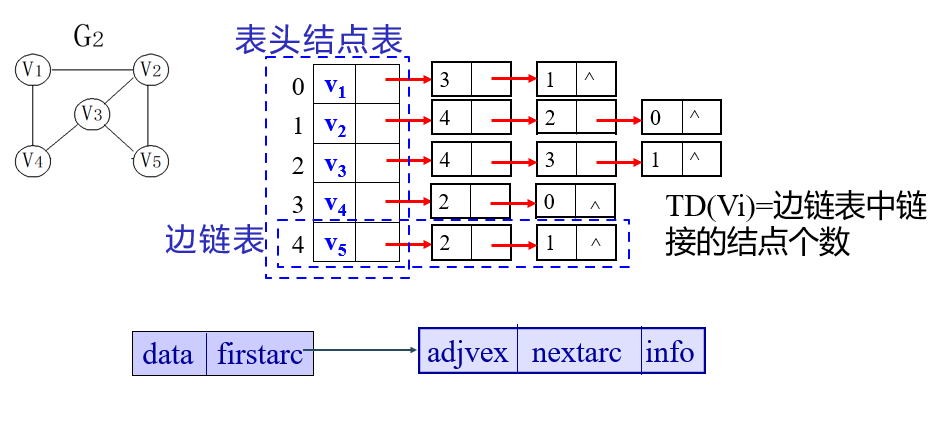
Adjacency List is a chain storage structure of graph. In the adjacency table, for each vertex v in the graph; Establish a single linked list and put the vertices adjacent to V in this linked list. The first node of each single linked list in the adjacency table stores information about vertices. This node is regarded as the header of the linked list, and the other nodes store information about edges. In this way, the adjacency table is composed of two parts: header node table and edge table.
Adjacency table representation of undirected graph
Adjacency table representation of directed graph
//Adjacency table storage representation of graph
#define MVNum 100 / / maximum number of vertices
typedef struct ArcNode
{
int adjvex; // The position of the vertex that the edge points to
struct ArcNode *nextarc; // Pointer to the next edge
OtherInfo info; // Edge related information
} ArcNode;
typedef struct VNode
{
VertexType data; // Vertex information
ArcNode *firstarc; // Points to the first edge attached to the vertex
} VNode, AdjList[MVNum]; // AdjList indicates the adjacency table type
typedef struct
{
AdjList vertices; // vertices - the complex number of vertex
int vexnum, arcnum; //The current number of vertices and edges of a graph
} ALGraph;
Using adjacency table representation to create undirected graph
- Enter the total number of vertices and sides.
- Input the information of points in turn and store it in the vertex table to initialize the pointer field of each header node to NULL.
- Create an adjacency table. Enter the two vertices attached to each edge in turn, determine the sequence numbers i and j of the two vertices, and insert the edge node into the heads of the two edge linked lists corresponding to vi and vj respectively.
Status CreateUDG(ALGraph &G)
{ //Using adjacency table representation, undirected graph G is created
cin >> G.vexnum >> G.arcnum; //Enter the number of vertices and arcs
for (i = 0; i < G.vexnum; ++i)
{ //Input each point to construct the header node table
cin >> G.vertices[i].data; //Enter vertex value
G.vertices[i].firstarc = NULL; //The pointer field of the initialization header node is NULL
}
for (k = 0; k < G.arcnum; ++k) //Input each side, construct adjacency table, head interpolation
{
cin >> v1 >> v2; //Enter the two vertices to which an edge is attached
i = LocateVex(G, v1);
j = LocateVex(G, v2);
p1 = new ArcNode; //Generate a new edge node * p1
p1->adjvex = j; //The serial number of adjacent points is j
p1->nextarc = G.vertices[i].firstarc;
G.vertices[i].firstarc = p1; //Insert the new node * p1 into the edge table header of vertex vi
p2 = new ArcNode; //Generate a new edge node * p2
p2->adjvex = i; //The serial number of adjacent points is j
p2->nextarc = G.vertices[j].firstarc; //Insert arc node into single linked list
G.vertices[j].firstarc = p2; //Insert the new node * p2 into the edge table header of vertex vj
} //Head insertion
return OK;
} // CreateUDG
The time complexity of the algorithm is O(n+e).
The establishment of adjacency list of directed graph is similar to this, but it is more simple. For each vertex pair sequence number < I, j >, it only needs to generate an edge list node with adjacent node sequence number j and insert it into the head of edge linked list of v. To create the adjacency table of the net, you can store the weight of the edge in the info field.
Comparison between adjacency matrix and adjacency table

Example 1:
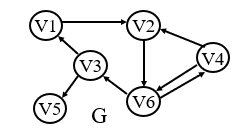
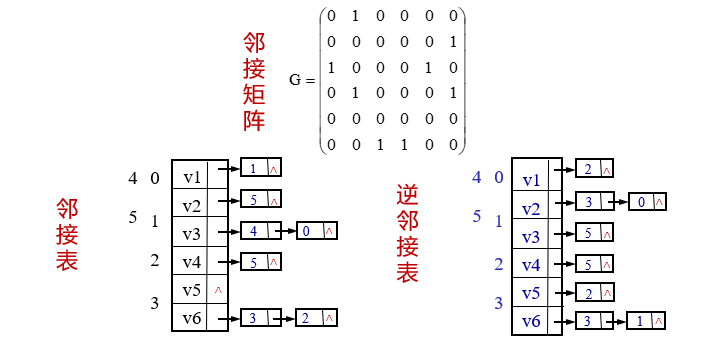
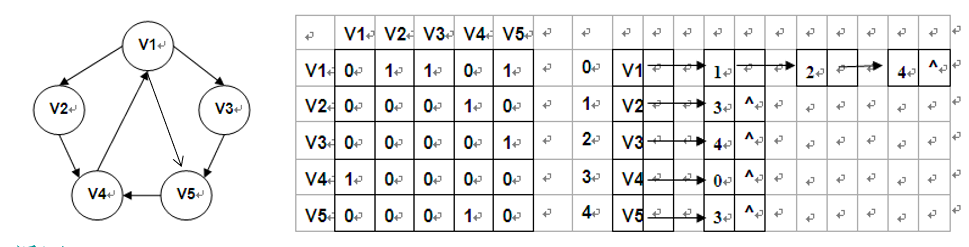
Example 2:

④. Orthogonal list
Orthogonal list is another chain storage structure of directed graph. It can be regarded as a linked list obtained by combining the adjacency list and inverse adjacency list of directed graph. In the cross linked list, there is a node corresponding to each arc in the directed graph and a node corresponding to each vertex.
There are five fields in the arc node: the tail field and the head field indicate the positions of the two vertices of the arc tail and the arc head in the graph respectively. The chain field hlink points to the next arc with the same arc head, the chain field tlink points to the next arc with the same arc tail, and the info field points to the relevant information of the arc. The arc with the same arc head is on the same linked list, and the arc with the same arc tail is also on the same linked list. Their head node is the vertex node, which is composed of three fields: the data field stores the information related to the vertex, such as the name of the vertex; firstin and firstout are two chain domains, which point to the first arc node with the vertex as the arc head or tail respectively.
| name | explain |
|---|---|
| tailvex | Indicates the position of the arc tail vertex in the graph. |
| headtex | Indicates the position of the arc head vertex in the graph. |
| hlink | Is the pointer to the next arc with the same arc head. |
| tlink | Is the pointer to the next arc with the same tail. |
| Info | Information pointing to the arc. |
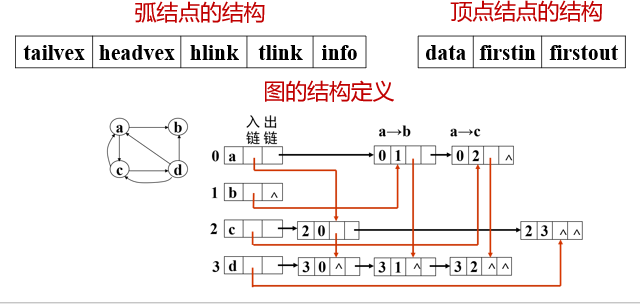
//Cross linked list storage representation of directed graph
#define MAX_VERTEX_NUM 20
typedef struct ArcBox
{
int tailvex, headvex;
struct ArcBox *hlink, *tlink;
InfoType *info;
} ArcBox;
typedef struct VexNode // ArcBox is an arc node variable
{
VertexType data;
ArcBox *firstin, *firstout;
} VexNode;
typedef struct // VexNode is a vertex variable
{
VexNode xlist[MAX_VERTEX_NUM]; // Heading direction
int vexnum, arcnum; // Current vertex number and arc number of digraph
} OLGraph;
Example:
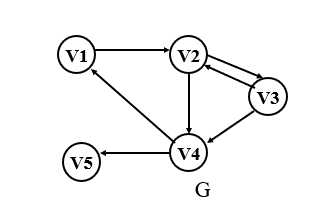
④. Adjacency multiple table
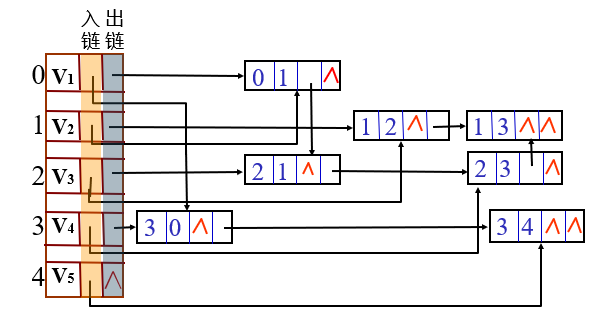
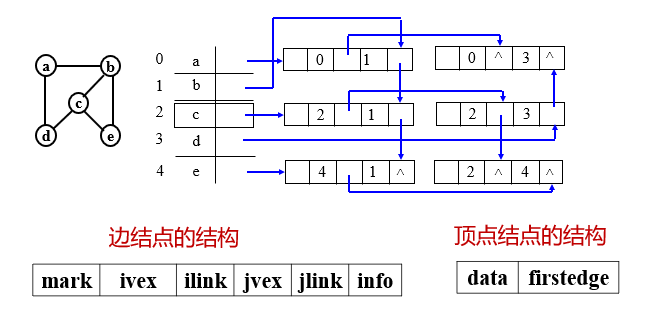
Adjacency multiple list is another chain storage structure of undirected graph. Although it is easy to obtain various information of vertices and edges when storing undirected graph with adjacency list, each edge in adjacency list has two nodes, which are in the i and j chain lists respectively, which brings inconvenience to some operations of graph. In the adjacency multiple table, each edge has only one edge node, which provides convenience for the processing of related edges.
| name | explain |
|---|---|
| mark | Is a flag field, which can be used to mark whether the edge has been searched |
| ivex and jvex | The positions of the two vertices attached to the edge in the graph; |
| ilnk | Point to the next edge attached to vertex ivex; |
| jlink | Point to the next edge attached to the vertex jvex |
| info | Is a pointer field pointing to various information related to edges. |
Example:
//Storage adjacency graph without adjacency table
#define MAX_VERTEX_NUM 20
typedef enum
{
unvisited,
viseited
} ViseitIF;
typedef struct EBox
{
VisitIf mark; //Access flag field
int ivex, jvex; //The two vertices to which the edge is attached are located in the header array
struct EBox *ilink, *jlink; //Point to the next edge attached to ivex and jvex, respectively
InfoType *info;
} Ebox;
typedef struct VexBox
{
VertexType data; //Save information about vertices
EBox *firstedge; //Points to the first edge attached to the vertex
} VexBox;
typedef struct
{
VexBox adjmulist[MAX_VERTEX_NUM]; // Header vector
int vexnum, edgenum; // Current vertex number and arc number of undirected graph
} AMLGraph;
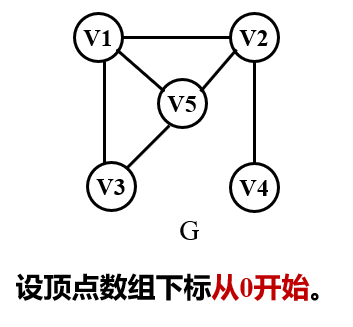
Example: draw the adjacency multiple table of undirected graph G
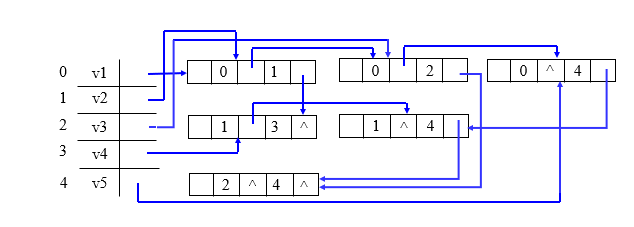

4. Traversal of Graphs
V from a vertex in the graph. To access all vertices in a graph along some edges and make each vertex accessed once and only once is called graph traversal. It is the basic operation of graph.
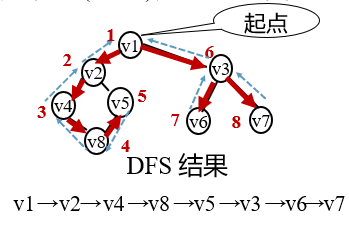
①. Depth first search
Depth First Search (DFS) traversal is similar to the prior traversal of a tree and is a generalization of the prior traversal of a tree. For a connected graph, the Depth First Search traversal process is as follows.
- Starting from a vertex v in the graph, access v.
- Find the first unreachable adjacency point of the vertex just accessed and access the vertex. Take this vertex as a new vertex and repeat this step until the vertex just accessed has no adjacent points that have not been accessed.
- Return to the vertex that has been visited and still has an unreachable adjacency point, find the next unreachable adjacency point of the vertex, and access the vertex.
- Repeat steps (2) and (3) until all vertices in the graph have been accessed and the search ends.
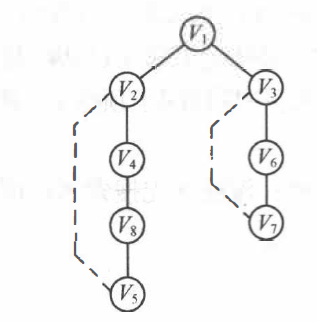
For undirected connected graphs, if the edge preservation passed by the forward operation during a depth first search is left, a depth first search spanning tree can be formed.
Implementation of depth first search traversal algorithm
Obviously, depth first search traversing a connected graph is a recursive process. In order to distinguish whether a vertex has been accessed during traversal, it is necessary to attach an access flag array visited[n], whose initial value is "false". Once a vertex is accessed, its corresponding component is set to "true".
- Starting from a vertex v in the graph, access V and collocate the value of visited[y] to true.
- Check all adjacency points w of v in turn. If the value of visited[w] is false, start from W and iterate recursively until all vertices in the graph have been accessed.
//Recursive algorithm of depth first search traversing connected graph
#include <iostream>
using namespace std;
#define MVNum 100 / / maximum number of vertices
typedef char VerTexType; //Assume that the data type of the vertex is character type
typedef int ArcType; //It is assumed that the weight type of the edge is integer
typedef struct
{
VerTexType vexs[MVNum]; //Vertex table
ArcType arcs[MVNum][MVNum]; //adjacency matrix
int vexnum, arcnum; //Current number of points and edges of a graph
} Graph;
bool visited[MVNum]; //Access the flag array whose initial value is "false"
int FirstAdjVex(Graph G, int v); //Returns the first adjacent contact of v
int NextAdjVex(Graph G, int v, int w); //Returns the next adjacent node of v relative to w
int LocateVex(Graph G, VerTexType v)
{
//Determine the position of point v in G
for (int i = 0; i < G.vexnum; ++i)
if (G.vexs[i] == v)
return i;
return -1;
} // LocateVex
void CreateUDN(Graph &G)
{
//The adjacency matrix representation is used to create undirected network G
int i, j, k;
cout << "Please enter the total number of vertices and sides , Separated by spaces:";
cin >> G.vexnum >> G.arcnum; //Enter the total number of vertices and edges
cout << endl;
cout << "Enter a name for the point, such as a: " << endl;
for (i = 0; i < G.vexnum; ++i)
{
cout << "Please enter page" << (i + 1) << "Name of the first point:";
cin >> G.vexs[i]; //Enter the information of the points in turn
}
cout << endl;
for (i = 0; i < G.vexnum; ++i) //Initialize the adjacency matrix, and set the weights of the edges to the maximum MaxInt
for (j = 0; j < G.vexnum; ++j)
G.arcs[i][j] = 0;
cout << "Enter the vertex to which the edge is attached, such as: a b" << endl;
for (k = 0; k < G.arcnum; ++k)
{ //Construct adjacency matrix
VerTexType v1, v2;
cout << "Please enter page" << (k + 1) << "Vertex to which an edge is attached:";
cin >> v1 >> v2; //Enter the vertex and weight of an edge
i = LocateVex(G, v1);
j = LocateVex(G, v2); //Determine the position of v1 and v2 in G, that is, the subscript of the vertex group
G.arcs[j][i] = G.arcs[i][j] = 1; //Set the weight of the symmetrical edge < V2, V1 > of < V1, V2 > to w
} // for
} // CreateUDN
void DFS(Graph G, int v)
{ //Starting from the v-th vertex, recursively traverse graph G with depth first
cout << G.vexs[v] << " ";
visited[v] = true; //Access the v-th vertex and collocate the corresponding component value of the access flag array to true
int w;
for (w = FirstAdjVex(G, v); w >= 0; w = NextAdjVex(G, v, w))
//Check all adjacent points w of v in turn. FirstAdjVex(G, v) represents the first adjacent point of v
// NextAdjVex(G, v, w) indicates the next adjacent point of v relative to W, and w ≥ 0 indicates the existence of adjacent points
if (!visited[w])
DFS(G, w); //DFS is called recursively on the adjacent vertex w of v that has not been accessed
} // DFS
int FirstAdjVex(Graph G, int v)
{
int i;
for (i = 0; i < G.vexnum; ++i)
{
if (G.arcs[v][i] == 1 && visited[i] == false)
return i;
}
return -1;
} // FirstAdjVex
int NextAdjVex(Graph G, int v, int w)
{
int i;
for (i = w; i < G.vexnum; ++i)
{
if (G.arcs[v][i] == 1 && visited[i] == false)
return i;
}
return -1;
} // NextAdjVex
int main()
{
cout << "************Recursive algorithm of depth first search traversing connected graph**************" << endl
<< endl;
Graph G;
CreateUDN(G);
cout << endl;
cout << "Undirected connected graph G Creation completed!" << endl
<< endl;
cout << "Please enter the starting point of traversing the connected graph:";
VerTexType c;
cin >> c;
int i;
for (i = 0; i < G.vexnum; ++i)
{
if (c == G.vexs[i])
break;
}
cout << endl;
while (i >= G.vexnum)
{
cout << "This point does not exist, please re-enter!" << endl;
cout << "Please enter the starting point of traversing the connected graph:";
cin >> c;
for (i = 0; i < G.vexnum; ++i)
{
if (c == G.vexs[i])
break;
}
}
cout << "Depth first search traversal connected graph results:" << endl;
DFS(G, i);
cout << endl;
return 0;
} // main
//Depth first search traversal unconnected graph
#include <iostream>
using namespace std;
#define MVNum 100 / / maximum number of vertices
typedef char VerTexType; //Assume that the data type of the vertex is character type
typedef int ArcType; //It is assumed that the weight type of the edge is integer
//-------------Adjacency matrix of graph-----------------
typedef struct
{
VerTexType vexs[MVNum]; //Vertex table
ArcType arcs[MVNum][MVNum]; //adjacency matrix
int vexnum, arcnum; //Current number of points and edges of a graph
} Graph;
bool visited[MVNum]; //Access the flag array whose initial value is "false"
int FirstAdjVex(Graph G, int v); //Returns the first adjacent contact of v
int NextAdjVex(Graph G, int v, int w); //Returns the next adjacent node of v relative to w
int LocateVex(Graph G, VerTexType v)
{
//Determine the position of point v in G
for (int i = 0; i < G.vexnum; ++i)
if (G.vexs[i] == v)
return i;
return -1;
} // LocateVex
void CreateUDN(Graph &G)
{
//The adjacency matrix representation is used to create undirected network G
int i, j, k;
cout << "Please enter the total number of vertices and sides, separated by spaces:";
cin >> G.vexnum >> G.arcnum; //Enter the total number of vertices and edges
cout << endl;
cout << "Enter a name for the point, such as a" << endl;
for (i = 0; i < G.vexnum; ++i)
{
cout << "Please enter page" << (i + 1) << "Name of the first point:";
cin >> G.vexs[i]; //Enter the information of the points in turn
}
cout << endl;
for (i = 0; i < G.vexnum; ++i) //Initialize the adjacency matrix, and set the weights of the edges to the maximum MaxInt
for (j = 0; j < G.vexnum; ++j)
G.arcs[i][j] = 0;
cout << "Enter the vertex to which the edge is attached, such as a b" << endl;
for (k = 0; k < G.arcnum; ++k)
{ //Construct adjacency matrix
VerTexType v1, v2;
cout << "Please enter page" << (k + 1) << "Vertex to which an edge is attached:";
cin >> v1 >> v2; //Enter the vertex and weight of an edge
i = LocateVex(G, v1);
j = LocateVex(G, v2); //Determine the position of v1 and v2 in G, that is, the subscript of the vertex group
G.arcs[j][i] = G.arcs[i][j] = 1; //Set the weight of the symmetrical edge < V2, V1 > of < V1, V2 > to w
} // for
} // CreateUDN
void DFS(Graph G, int v)
{
//Starting from the v-th vertex, recursively traverse graph G with depth first
cout << G.vexs[v] << " ";
visited[v] = true; //Access the v-th vertex and collocate the corresponding component value of the access flag array to true
int w;
for (w = FirstAdjVex(G, v); w >= 0; w = NextAdjVex(G, v, w))
//Check all adjacent points w of v in turn. FirstAdjVex(G, v) represents the first adjacent point of v
// NextAdjVex(G, v, w) indicates the next adjacent point of v relative to W, and w ≥ 0 indicates the existence of adjacent points
if (!visited[w])
DFS(G, w); //DFS is called recursively on the adjacent vertex w of v that has not been accessed
} // DFS
void DFSTraverse(Graph G)
{
//Depth first traversal of unconnected graph G
int v;
for (v = 0; v < G.vexnum; ++v)
visited[v] = false; //Access flag array initialization
for (v = 0; v < G.vexnum; ++v) //Loop call algorithm 6.3
if (!visited[v])
DFS(G, v); //Call DFS on vertices that have not been accessed
} // DFSTraverse
int FirstAdjVex(Graph G, int v)
{
//Returns the first adjacent contact of v
int i;
for (i = 0; i < G.vexnum; ++i)
{
if (G.arcs[v][i] == 1 && visited[i] == false)
return i;
}
return -1;
} // FirstAdjVex
int NextAdjVex(Graph G, int v, int w)
{
//Returns the next adjacent node of v relative to w
int i;
for (i = w; i < G.vexnum; ++i)
{
if (G.arcs[v][i] == 1 && visited[i] == false)
return i;
}
return -1;
} // NextAdjVex
int main()
{
cout << "************Depth first search traversal unconnected graph**************" << endl
<< endl;
Graph G;
CreateUDN(G);
cout << endl;
cout << "Undirected graph G Creation completed!" << endl
<< endl;
cout << "Depth first search traversal unconnected graph results:" << endl;
DFSTraverse(G);
cout << endl;
return 0;
} // main
②. Breadth first search
Breadth First Search (BFS) traversal is similar to the hierarchical traversal of a tree.
The breadth first search traversal process is as follows.
- Starting from a vertex v in the graph, access v.
- Access v's previously inaccessible adjacency points in turn.
- Starting from these adjacency points, access their adjacency points in turn, and make the "adjacency point of the first accessed vertex" be accessed before the "adjacency point of the later accessed vertex". Repeat step 3 until the adjacency points of all accessed vertices in the graph are accessed.
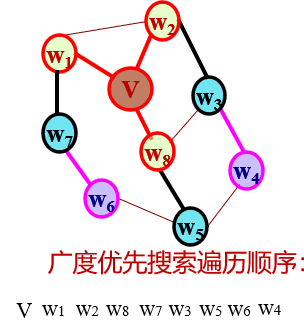
Breadth first spanning tree:
Breadth first search traversal connected graph
- Starting from a vertex v in the graph, access V, and set the value of visited[y] to true, and then queue v.
- As long as the queue is not empty, repeat the following operations:
-Team leader u out of the team;
-Check all adjacency points w of u in turn. If the value of visited[w] is false, access W, and set the value of visited[w] to true, and then queue W.
//Breadth first search traversal connected graph
#include <iostream>
using namespace std;
#define MVNum 100 // max vertex
#define MAXQSIZE 100 // Maximum queue length
typedef char VerTexType; //Assume that the data type of the vertex is character type
typedef int ArcType; //It is assumed that the weight type of the edge is integer
bool visited[MVNum]; //Access the flag array whose initial value is "false"
//-----Storage representation of adjacency matrix of graph-----
typedef struct{
VerTexType vexs[MVNum]; //Vertex table
ArcType arcs[MVNum][MVNum]; //adjacency matrix
int vexnum,arcnum; //Current number of points and edges of a graph
}Graph;
//----Definition and operation of queue--------
typedef struct{
ArcType *base; //Initialized dynamically allocated storage space
int front; //Header pointer. If the queue is not empty, it points to the queue header element
int rear; //Tail pointer. If the queue is not empty, it points to the next position of the tail element
}sqQueue;
void InitQueue(sqQueue &Q){
//Construct an empty queue Q
Q.base = new ArcType[MAXQSIZE];
if(!Q.base) exit(1); //Storage allocation failed
Q.front = Q.rear = 0;
}//InitQueue
void EnQueue(sqQueue &Q, ArcType e){
//Insert a new tail element with element e as Q
if((Q.rear + 1) % MAXQSIZE == Q.front)
return;
Q.base[Q.rear] = e;
Q.rear = (Q.rear + 1) % MAXQSIZE;
}//EnQueue
bool QueueEmpty(sqQueue Q){
//Determine whether it is an empty team
if(Q.rear == Q.front)
return true;
return false;
}//QueueEmpty
void DeQueue(sqQueue &Q, ArcType &u){
//The team head element is out of the team and placed as u
u = Q.base[Q.front];
Q.front = (Q.front + 1) % MAXQSIZE;
}//DeQueue
//--------------------------------------------------
int LocateVex(Graph G , VerTexType v){
//Determine the position of point v in G
for(int i = 0; i < G.vexnum; ++i)
if(G.vexs[i] == v)
return i;
return -1;
}//LocateVex
void CreateUDN(Graph &G){
//The adjacency matrix representation is used to create undirected network G
int i , j , k;
cout <<"Please enter the total number of vertices and sides, separated by spaces:";
cin >> G.vexnum >> G.arcnum; //Enter the total number of vertices and edges
cout << endl;
cout << "Enter a name for the point, such as a" << endl;
for(i = 0; i < G.vexnum; ++i){
cout << "Please enter page" << (i+1) << "Name of the first point:";
cin >> G.vexs[i]; //Enter the information of the points in turn
}
cout << endl;
for(i = 0; i < G.vexnum; ++i) //Initialize the adjacency matrix, and set the weights of the edges to the maximum MaxInt
for(j = 0; j < G.vexnum; ++j)
G.arcs[i][j] = 0;
cout << "Enter the vertex to which the edge is attached, such as a b" << endl;
for(k = 0; k < G.arcnum;++k){ //Construct adjacency matrix
VerTexType v1 , v2;
cout << "Please enter page" << (k + 1) << "Vertex to which an edge is attached:";
cin >> v1 >> v2; //Enter the vertex to which an edge is attached
i = LocateVex(G, v1); j = LocateVex(G, v2); //Determine the position of v1 and v2 in G, that is, the subscript of the vertex group
G.arcs[i][j] = 1; //The weight of edge < V1, V2 > is set to w
G.arcs[j][i] = G.arcs[i][j]; //Set the weight of the symmetrical edge < V2, V1 > of < V1, V2 > to w
}//for
}//CreateUDN
int FirstAdjVex(Graph G , int v){
//Returns the first adjacent contact of v
int i;
for(i = 0 ; i < G.vexnum ; ++i){
if(G.arcs[v][i] == 1 && visited[i] == false)
return i;
}
return -1;
}//FirstAdjVex
int NextAdjVex(Graph G , int u , int w){
//Returns the next adjacent node of v relative to w
int i;
for(i = w ; i < G.vexnum ; ++i){
if(G.arcs[u][i] == 1 && visited[i] == false)
return i;
}
return -1;
}//NextAdjVex
void BFS (Graph G, int v){
//Non recursive traversal of connected graph G by breadth first
sqQueue Q;
ArcType u;
ArcType w;
cout << G.vexs[v] << " "; visited[v] = true; //Access the v-th vertex and collocate the corresponding component value of the access flag array to true
InitQueue(Q); //Auxiliary queue Q initialization, null
EnQueue(Q, v); //v join the team
while(!QueueEmpty(Q)){ //Queue is not empty
DeQueue(Q, u); //The team head element is out of the team and placed as u
for(w = FirstAdjVex(G, u); w >= 0; w = NextAdjVex(G, u, w)){
//Check all adjacent points w of u in turn. FirstAdjVex(G, u) represents the first adjacent point of U
//NextAdjVex(G, u, w) indicates the next adjacent point of u relative to W, and w ≥ 0 indicates the existence of adjacent points
if(!visited[w]){ //Adjacent vertices not yet accessed with w as u
cout << G.vexs[w] << " "; visited[w] = true; //Access w, and the corresponding component value of the collocated access flag array is true
EnQueue(Q, w); //w into the team
}//if
}//for
}//while
}//BFS
int main(){
cout << "************Algorithm breadth first search traversal connected graph**************" << endl << endl;
Graph G;
CreateUDN(G);
cout << endl;
cout << "Undirected connected graph G Creation completed!" << endl << endl;
cout << "Please enter the starting point of traversing the connected graph:";
VerTexType c;
cin >> c;
int i;
for(i = 0 ; i < G.vexnum ; ++i){
if(c == G.vexs[i])
break;
}
cout << endl;
while(i >= G.vexnum){
cout << "This point does not exist, please re-enter!" << endl;
cout << "Please enter the starting point of traversing the connected graph:";
cin >> c;
for(i = 0 ; i < G.vexnum ; ++i){
if(c == G.vexs[i])
break;
}
}
cout << "Depth first search traversal connected graph results:" << endl;
BFS(G , i);
cout <<endl;
return 0;
}//main
5. Application of graph
①. minimum spanning tree
Minimal connected subgraph: the subgraph is a connected subgraph of G. if any edge is deleted from the subgraph, the subgraph is no longer connected.
Spanning tree: a minimal connected subgraph containing all vertices of graph G
The vertex set of spanning tree is equal to that of graph, and the number of vertices is n; There is no loop and the number of sides is n-1
In the multiple spanning trees of the network, find a spanning tree with the smallest sum of the weights of each edge, that is, the smallest spanning tree
Criteria for constructing minimum spanning tree:
- Only the edges in the net must be used to construct the minimum spanning tree;
- You must use and only use n-1 edges to join n vertices in the network
- Edges that produce loops cannot be used
Prim algorithm (point adding method)
Suppose N=(V,E) is a connected network and TE is the set of edges in the minimum spanning tree on N.
- U= {u0}(u0∈V),TE={}.
- Among all the edges (u,v) ∈ E of u ∈ u, v ∈ V-U, find an edge (u0, v0) with the smallest weight to merge into the set TE, and v0 is merged into U.
- Repeat ② until U=V.
At this time, there must be n-1 edges in te, then T=(V, TE) is the minimum spanning tree of N.
The process of constructing the minimum spanning tree by prim algorithm:
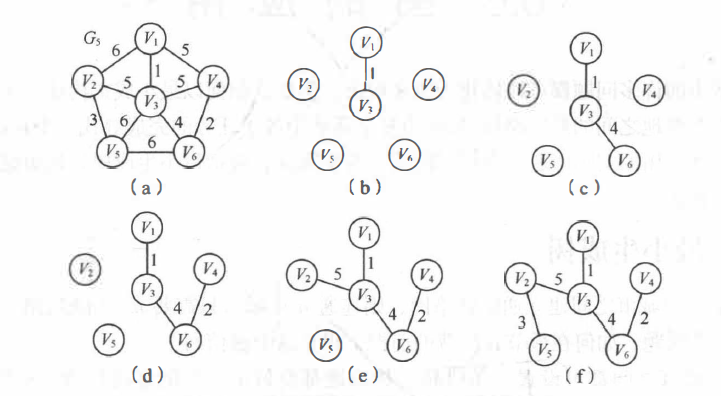
The graph is stored by adjacency matrix, and a two-dimensional array closedeg is used to record the edges with the lowest cost from U to V-U.
For each vertex vi, v-U, there is a corresponding component closedge[i-1] in the auxiliary array, which includes two fields:
typedef struct
{
VertexType adjvex; // Vertex of the smallest edge
VRType lowcost; // Weight of the smallest edge
} closedge[MAX_VERTEX_NUM];
adjvex: another vertex attached to this least cost edge.
- Equal to 0 means that vertex i is already in U;
- Greater than 0 indicates that vertex i is still in V-U.
Therefore, in each cycle, the vertex with the smallest lowcast must be selected from those vertices with lowcast > 0 (in the set V-U) to be added to the set u, and the closedge of relevant vertices shall be adjusted accordingly.
//Prim algorithm
#include <iostream>
using namespace std;
typedef char VerTexType;
typedef int ArcType;
#define MVNum 100
#define MaxInt 32767 // Represents the maximum value, i.e. ∞
//The definition of auxiliary array is used to record the edge with the smallest weight from vertex set U to V-U
struct{
VerTexType adjvex; //The vertex of the smallest edge in U
ArcType lowcost; //Weight on minimum edge
}closedge[MVNum];
//----- adjacency table storage representation of graph -----
typedef char VerTexType; //Assume that the data type of the vertex is character type
typedef int ArcType; //It is assumed that the weight type of the edge is integer
typedef struct{
VerTexType vexs[MVNum]; //Vertex table
ArcType arcs[MVNum][MVNum]; //adjacency matrix
int vexnum,arcnum; //Current number of points and edges of a graph
}AMGraph;
int LocateVex(AMGraph G , VerTexType v){
//Determine the position of point v in G
for(int i = 0; i < G.vexnum; ++i)
if(G.vexs[i] == v)
return i;
return -1;
}//LocateVex
void CreateUDN(AMGraph &G){
//The adjacency matrix representation is used to create undirected network G
int i , j , k;
cout <<"Please enter the total number of vertices and sides, separated by spaces:";
cin >> G.vexnum >> G.arcnum; //Enter the total number of vertices and edges
cout << endl;
cout << "Enter a name for the point, such as a" << endl;
for(i = 0; i < G.vexnum; ++i){
cout << "Please enter page" << (i+1) << "Name of the first point:";
cin >> G.vexs[i]; //Enter the information of the points in turn
}
cout << endl;
for(i = 0; i < G.vexnum; ++i) //Initialize the adjacency matrix, and set the weights of the edges to the maximum MaxInt
for(j = 0; j < G.vexnum; ++j)
G.arcs[i][j] = MaxInt;
cout << "Enter the vertex and weight of the edge, such as a b 5" << endl;
for(k = 0; k < G.arcnum;++k){ //Construct adjacency matrix
VerTexType v1 , v2;
ArcType w;
cout << "Please enter page" << (k + 1) << "Vertex and weight of edge attachment:";
cin >> v1 >> v2 >> w; //Enter the vertex and weight of an edge
i = LocateVex(G, v1); j = LocateVex(G, v2); //Determine the position of v1 and v2 in G, that is, the subscript of the vertex group
G.arcs[i][j] = w; //The weight of edge < V1, V2 > is set to w
G.arcs[j][i] = G.arcs[i][j]; //Set the weight of the symmetrical edge < V2, V1 > of < V1, V2 > to w
}//for
}//CreateUDN
int Min(AMGraph G){
//Returns the point with the lowest weight
int i;
int index = -1;
int min = MaxInt;
for(i = 0 ; i < G.vexnum ; ++i){
if(min > closedge[i].lowcost && closedge[i].lowcost != 0){
min = closedge[i].lowcost;
index = i;
}
}//for
return index;
}//Min
void MiniSpanTree_Prim(AMGraph G, VerTexType u){
//Undirected net G is stored in the form of adjacency matrix. Starting from vertex u, the minimum spanning tree T of G is constructed, and the edges of T are output
int k , j , i;
VerTexType u0 , v0;
k =LocateVex(G, u); //k is the subscript of vertex u
for(j = 0; j < G.vexnum; ++j){ //Initialize closedge[i] for each vertex vi of V-U
if(j != k){
closedge[j].adjvex = u;
closedge[j].lowcost = G.arcs[k][j]; //{adjvex, lowcost}
}//if
}//for
closedge[k].lowcost = 0; //Initial, U = {u}
for(i = 1; i < G.vexnum; ++i){ //Select the remaining n-1 vertices to generate n-1 edges (n= G.vexnum)
k = Min(G);
//Find the next node of T: the k-th vertex. There is the current minimum edge in closedge[k]
u0 = closedge[k].adjvex; //u0 is a vertex of the smallest edge, u0 ∈ U
v0 = G.vexs[k]; //v0 is the other vertex of the smallest edge, v0 ∈ V-U
cout << "edge " <<u0 << "--->" << v0 << endl; //Output the current minimum edge (u0, v0)
closedge[k].lowcost = 0; //The k th vertex is merged into the U set
for(j = 0; j < G.vexnum; ++j)
if(G.arcs[k][j] < closedge[j].lowcost){ //Reselect the smallest edge after the new vertex is merged into U
closedge[j].adjvex = G.vexs[k];
closedge[j].lowcost = G.arcs[k][j];
}//if
}//for
}//MiniSpanTree_Prim
int main(){
cout << "************Prim algorithm**************" << endl << endl;
AMGraph G;
CreateUDN(G);
cout << endl;
cout << "Undirected graph G Creation completed!" << endl;
cout <<endl;
cout << "******Using prim algorithm to construct the minimum spanning tree result:******" << endl;
MiniSpanTree_Prim(G , 'a');
cout <<endl;
return 0;
}//main
Example:

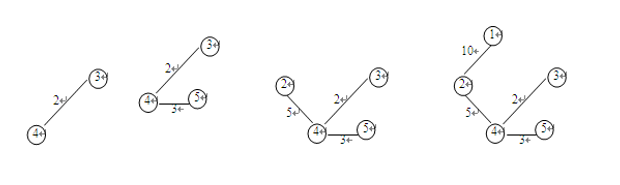
Kruskal algorithm (edging method)
Assuming the connected network N=(V,E), arrange the edges in Ⅳ in the order of weight from small to large.
- The initial state is a non connected graph with only n vertices and no edges, T=(V, {), and each vertex in the graph forms a connected component.
- Select the edge with the smallest weight in E. if the vertex attached to the edge falls on different connected components in t (i.e. no loop is formed), the edge will be added to T. otherwise, the edge will be rounded off and the next edge with the smallest weight will be selected.
- Repeat ② until all vertices in T are on the same connected component.
The process of constructing the minimum spanning tree by Kruskal algorithm:
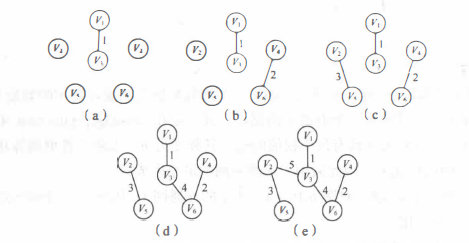
The implementation of the algorithm should introduce the following auxiliary data structure.
- Structure array Edge: stores the information of the Edge, including the two vertex information and weight of the Edge.
//Definition of auxiliary array Edges
struct
{
VerTexType Head; //Start point of edge
VerTexType Tail; //End of edge
ArcType lowcost; //Weight on edge
} Edge[arcnnum];
- Vexset[i]: identifies the connected component to which each vertex belongs. For each vertex v,EV, there is a corresponding element Vexset[i] in the auxiliary array to represent the connected component of the vertex. Initially, Vexset[i]=i, indicating that each vertex forms a connected component.
//Definition of auxiliary array Vexset int Vexset[MVNum];
- Sort the elements in the array Edge by weight from small to large.
- View the edges in the array Edge in turn and cycle through the following operations:
- Select an Edge (U1,U2) from the ordered array Edge in turn;
- Find the connected components vs1 and vs2 of v1 and v2 in Vexset and judge:
-If vs1 and vs2 are not equal, it indicates that the selected two vertices belong to different connected components, output this edge, and merge the two connected components of vs1 and vs2;
-If vs1 and vs2 are equal, it indicates that the selected two vertices belong to the same connected component. This edge is rounded off and the next edge with the lowest weight is selected.
//Kruskal algorithm
#include <iostream>
using namespace std;
typedef char VerTexType; //Assume that the data type of the vertex is character type
typedef int ArcType;
#define MVNum 100 // max vertex
#define MaxInt 32767 // Represents the maximum value, i.e. ∞
//----------------Adjacency matrix of graph---------------------
typedef struct{
VerTexType vexs[MVNum]; //Vertex table
ArcType arcs[MVNum][MVNum]; //adjacency matrix
int vexnum,arcnum; //Current number of points and edges of a graph
}AMGraph;
//Definition of auxiliary array Edges
struct{
VerTexType Head; //Start point of edge
VerTexType Tail; //End of edge
ArcType lowcost; //Weight on edge
}Edge[(MVNum * (MVNum - 1)) / 2];
int Vexset[MVNum]; //Definition of auxiliary array Vexset
int LocateVex(AMGraph G , VerTexType v){
//Determine the position of point v in G
for(int i = 0; i < G.vexnum; ++i)
if(G.vexs[i] == v)
return i;
return -1;
}//LocateVex
void CreateUDN(AMGraph &G){
//The adjacency matrix representation is used to create undirected network G
int i , j , k;
cout <<"Please enter the total number of vertices and sides, separated by spaces:";
cin >> G.vexnum >> G.arcnum; //Enter the total number of vertices and edges
cout << endl;
cout << "Enter a name for the point, such as a" << endl;
for(i = 0; i < G.vexnum; ++i){
cout << "Please enter page" << (i+1) << "Name of the first point:";
cin >> G.vexs[i]; //Enter the information of the points in turn
}
cout << endl;
for(i = 0; i < G.vexnum; ++i) //Initialize the adjacency matrix, and set the weights of the edges to the maximum MaxInt
for(j = 0; j < G.vexnum; ++j)
G.arcs[i][j] = MaxInt;
cout << "Enter the vertex and weight of the edge, such as a b 6" << endl;
for(k = 0; k < G.arcnum;++k){ //Construct adjacency matrix
VerTexType v1 , v2;
ArcType w;
cout << "Please enter page" << (k + 1) << "Vertex and weight of edge attachment:";
cin >> v1 >> v2 >> w; //Enter the vertex and weight of an edge
i = LocateVex(G, v1); j = LocateVex(G, v2); //Determine the position of v1 and v2 in G, that is, the subscript of the vertex group
G.arcs[i][j] = w; //The weight of edge < V1, V2 > is set to w
G.arcs[j][i] = G.arcs[i][j]; //Set the weight of the symmetrical edge < V2, V1 > of < V1, V2 > to w
Edge[k].lowcost = w;
Edge[k].Head = v1;
Edge[k].Tail = v2;
}//for
}//CreateUDN
//----------Bubble sorting-------------------
void Sort(AMGraph G){
int m = G.arcnum - 2;
int flag = 1;
while((m > 0) && flag == 1){
flag = 0;
for(int j = 0 ; j <= m ; j++){
if(Edge[j].lowcost > Edge[j+ 1].lowcost){
flag = 1;
VerTexType temp_Head = Edge[j].Head;
Edge[j].Head = Edge[j+ 1].Head;
Edge[j + 1].Head = temp_Head;
VerTexType temp_Tail = Edge[j].Tail;
Edge[j].Tail = Edge[j+ 1].Tail;
Edge[j + 1].Tail = temp_Tail;
ArcType temp_lowcost = Edge[j].lowcost;
Edge[j].lowcost = Edge[j+ 1].lowcost;
Edge[j + 1].lowcost = temp_lowcost;
}//if
}//for
--m;
}//while
}//Sort
void MiniSpanTree_Kruskal(AMGraph G){
//Undirected net G is stored in the form of adjacency matrix, constructs the minimum spanning tree T of G, and outputs each edge of T
int i , j , v1 , v2 , vs1 , vs2;
Sort(G); //Sort the elements in the array Edge by weight from small to large
for(i = 0; i < G.vexnum; ++i) //Auxiliary array, indicating that each vertex forms a connected component
Vexset[i] = i;
for(i = 0; i < G.arcnum; ++i){
//Check whether the edges in the ordered array Edge are on the same connected component
v1 =LocateVex(G, Edge[i].Head); //v1 is the subscript of the starting point Head of the edge
v2 =LocateVex(G, Edge[i].Tail); //v2 is the subscript of Tail, the end point of the edge
vs1 = Vexset[v1]; //Get the connected component vs1 where the starting point of Edge[i] is located
vs2 = Vexset[v2]; //Get the connected component vs2 where the end point of Edge[i] is located
if(vs1 != vs2){ //The two vertices of an edge belong to different connected components
cout << Edge[i].Head << "-->" << Edge[i].Tail << endl; //Output this edge
for(j = 0; j < G.vexnum; ++j) //Combine vs1 and vs2 components, that is, the two sets are numbered uniformly
if(Vexset[j] == vs2) Vexset[j] = vs1; //Set number vs2 is changed to vs1
}//if
}//for
}//MiniSpanTree_Kruskal
void main(){
cout << "************Kruskal algorithm**************" << endl << endl;
AMGraph G;
CreateUDN(G);
cout <<endl;
cout << "*****Undirected network G Creation completed!*****" << endl;
cout <<endl;
MiniSpanTree_Kruskal(G);
}///main

②. Shortest path
For a graph, there may be multiple paths from one vertex to another, and the number of edges in each path may be different. The path with the least number of edges is called the shortest path.
Shortest path: for a network (weighted graph), the sum of the weights of the edges passing from one vertex to another is called the weighted path length, and the one with the shortest weighted path length is called the shortest path
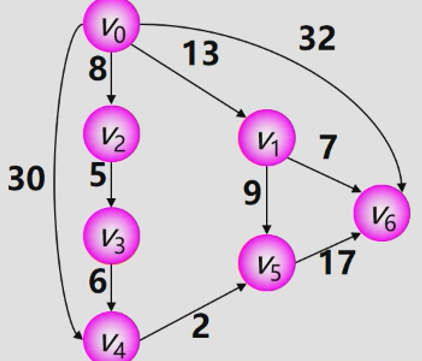
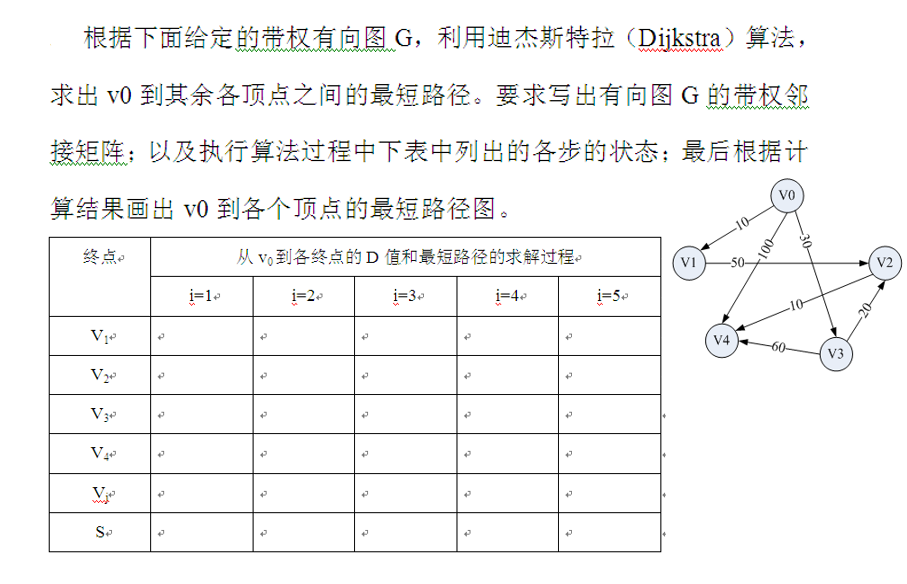
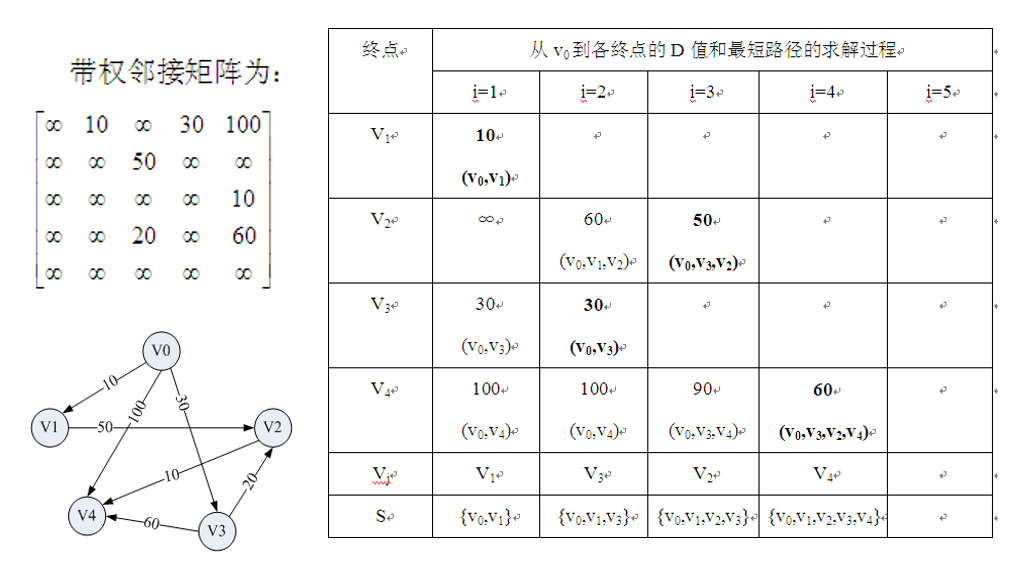
The shortest path from a source point to other vertices -- Dijkstra algorithm
- Initialization: first find the direct path (v0,vk) from the source point v0 to each end point v, that is, the path reached through an arc.
- Select: find a path with the shortest length (v0,u) from these paths.
- Update: then adjust the remaining paths appropriately.
If there are arcs (U, vk), (v0, u) +(u, vk) < (v0, vk) in the graph, replace (v0, vk) with path (v0,u,vk).
Among the adjusted paths, find the path with the shortest length.
Main storage structure: adjacency matrix G [n][n] (or adjacency table)
Secondary storage structure:
Array S[n]: record whether the shortest distance of the corresponding vertex has been determined
true: OK false: not OK
Array D[n]: record the path length from the source point to the corresponding vertex
Initial value: if there is an arc from v0 to vi, D[i] is the weight on the arc; Otherwise ∞
Array Path[n]: record the precursor vertex of the corresponding vertex
Initial value: if there is an arc from v0 to vi, Path[i] is V0, otherwise - 1
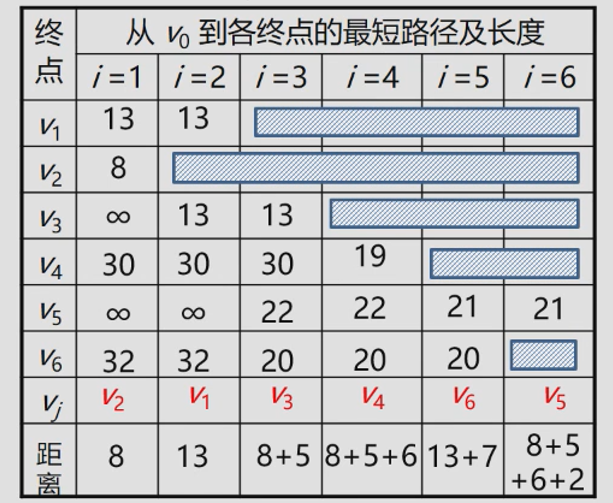
-
initialization:
Add the source point v0 to S, that is, S[v0] = true;
Initialize the shortest path length from v0 to each end point as the weight, that is, D[i]= G.arcs[v0][vi], (VI ∈ V -S);
If there is an arc between v0 and vertex vi, set the precursor of vi to v0, that is, Path[i] = v0, otherwise Path[i] = -1. -
Cycle n-1 times and perform the following operations:
Select the end point vk of the next shortest path so that: D[k]=Min{D[i]viEV-S}
Add vk to S, i.e. S[vk] = true.
Update the length of the shortest path from v0 to any vertex of the set V-S, and change the precursor of vi to vk.
If S[i]=false and D [k] + g.arcs [k] [i] < d [i], update D[i]-D[k]+ G.arcs[k][i; Path [i]=k;.
//Shortest path -- dijestra algorithm
#include <iostream>
using namespace std;
#define MaxInt 32767 // Represents the maximum value, i.e. ∞
#define MVNum 100 // max vertex
typedef char VerTexType; //Assume that the data type of the vertex is character type
typedef int ArcType; //It is assumed that the weight type of the edge is integer
int *D=new int[MVNum]; //Used to record the length of the shortest circuit
bool *S=new bool[MVNum]; //Mark whether the vertex enters the S set
int *Path=new int[MVNum]; //Precursor for recording the shortest vertex
//------------Adjacency matrix of graph-----------------
typedef struct{
VerTexType vexs[MVNum]; //Vertex table
ArcType arcs[MVNum][MVNum]; //adjacency matrix
int vexnum,arcnum; //Current number of points and edges of a graph
}AMGraph;
int LocateVex(AMGraph G , VerTexType v){
//Determine the position of point v in G
for(int i = 0; i < G.vexnum; ++i)
if(G.vexs[i] == v)
return i;
return -1;
}//LocateVex
void CreateUDN(AMGraph &G){
//The adjacency matrix representation is used to create undirected network G
int i , j , k;
cout <<"Please enter the total number of vertices and sides, separated by spaces:";
cin >> G.vexnum >> G.arcnum; //Enter the total number of vertices and edges
cout << endl;
cout << "Enter a name for the point:,as a" << endl;
for(i = 0; i < G.vexnum; ++i){
cout << "Please enter page" << (i+1) << "Name of the first point:";
cin >> G.vexs[i]; //Enter the information of the points in turn
}
cout << endl;
for(i = 0; i < G.vexnum; ++i) //Initialize the adjacency matrix, and set the weights of the edges to the maximum MaxInt
for(j = 0; j < G.vexnum; ++j)
G.arcs[i][j] = MaxInt;
cout << "Enter the vertex and weight of the edge, such as a b 7" << endl;
for(k = 0; k < G.arcnum;++k){ //Construct adjacency matrix
VerTexType v1 , v2;
ArcType w;
cout << "Please enter page" << (k + 1) << "Vertex and weight of edge attachment:";
cin >> v1 >> v2 >> w; //Enter the vertex and weight of an edge
i = LocateVex(G, v1); j = LocateVex(G, v2); //Determine the position of v1 and v2 in G, that is, the subscript of the vertex group
G.arcs[i][j] = w; //The weight of edge < V1, V2 > is set to w
G.arcs[j][i] = G.arcs[i][j]; //Set the weight of the symmetrical edge < V2, V1 > of < V1, V2 > to w
}//for
}//CreateUDN
void ShortestPath_DIJ(AMGraph G, int v0){
//Using Dijkstra algorithm to find the shortest path from v0 vertex of directed network G to other vertices
int v , i , w , min;
int n = G.vexnum; //n is the number of vertices in G
for(v = 0; v < n; ++v){ //n vertices are initialized in turn
S[v] = 0; //S is initially an empty set
D[v] = G.arcs[v0][v]; //Initialize the shortest path length from v0 to each end point as the weight on the arc
if(D[v] < MaxInt) Path [v] = v0; //If there is an arc between V0 and V, set the front drive of V to v0
else Path [v] = -1; //If there is no arc between v0 and v, set the front drive of v to - 1
}//for
S[v0]=true; //Add v0 to S
D[v0]=0; //The distance from the source point to the source point is 0
/*―After initialization, start the main loop, find the shortest path from v0 to a vertex v each time, and add V to S set --*/
for(i = 1;i < n; ++i){ //The remaining n-1 vertices are calculated in turn
min= MaxInt;
for(w = 0; w < n; ++w)
if(!S[w] && D[w] < min){ //Select a current shortest path, ending at v
v = w;
min = D[w];
}//if
S[v]=true; //Add v to S
for(w = 0;w < n; ++w) //Update from v0 to set V? The shortest path length of all vertices on S
if(!S[w] && (D[v] + G.arcs[v][w] < D[w])){
D[w] = D[v] + G.arcs[v][w]; //Update [w]
Path [w] = v; //Change the precursor of w to v
}//if
}//for
}//ShortestPath_DIJ
void DisplayPath(AMGraph G , int begin ,int temp ){
//Display the shortest circuit
if(Path[temp] != -1){
DisplayPath(G , begin ,Path[temp]);
cout << G.vexs[Path[temp]] << "-->";
}
}//DisplayPath
int main()
{
cout << "************Dijkstra's algorithm **************" << endl << endl;
AMGraph G;
int i , j ,num_start , num_destination;
VerTexType start , destination;
CreateUDN(G);
cout <<endl;
cout << "*****Undirected network G Creation completed!*****" << endl;
for(i = 0 ; i < G.vexnum ; ++i){
for(j = 0; j < G.vexnum; ++j){
if(j != G.vexnum - 1){
if(G.arcs[i][j] != MaxInt)
cout << G.arcs[i][j] << "\t";
else
cout << "∞" << "\t";
}
else{
if(G.arcs[i][j] != MaxInt)
cout << G.arcs[i][j] <<endl;
else
cout << "∞" <<endl;
}
}
}//for
cout << endl;
cout << "Please enter the start point and end point name in sequence:";
cin >> start >> destination;
num_start = LocateVex(G , start);
num_destination = LocateVex(G , destination);
ShortestPath_DIJ(G , num_start);
cout << endl <<"The shortest path is:";
DisplayPath(G , num_start , num_destination);
cout << G.vexs[num_destination]<<endl;
}//main
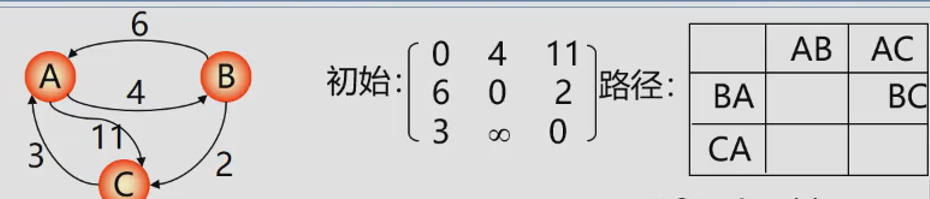
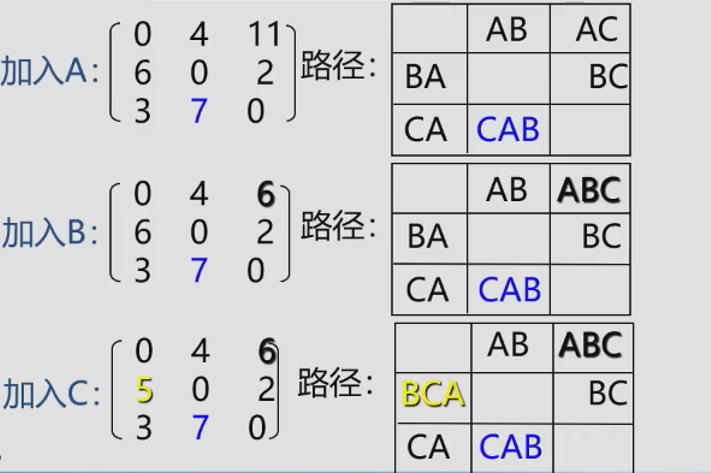
The shortest path between each pair of vertices -- Floyd algorithm
Starting from the weighted adjacency matrix G.arcs of the graph,
Suppose to find the shortest path from vertex Vi to Vj. If there is an arc from Vi to Vj, there is a path with a length of G.arcs[i]i] from Vi to Vj, but whether the path must be the shortest path still needs to be explored n times.
- For the first time, judge (Vi, V0) and (V0, Vj), that is, judge whether (Vi, V0, Vj) exists. If so, compare (Vi,
The length of Vj) and (Vi, V0, Vj), whichever is shorter, is the shortest path from Vi to Vj, and the sequence number of the middle vertex is not greater than 0. - The second time, add another vertex V1 if (Vi,..., V1) and (V1,
Vj) are the shortest paths with the sequence number of intermediate vertices not greater than 0, then (Vi,..., V1,
Vj) may be the shortest path from Vi to Vj with the middle vertex number not greater than 1. Compare it with the shortest path from Vi to Vj whose vertex number is not greater than 0, and take the shorter one as the shortest path from Vi to Vj whose middle vertex number is not greater than 1. - The third time, add another vertex V2 and continue the temptation.
To find the shortest path:
- Initially, set an n-order square matrix so that its diagonal element is 0. If there is an arc < VI, VJ >, the corresponding element is the weight; Otherwise, it is infinite.
- Gradually try to add intermediate vertices to the original direct path. If the path becomes shorter after adding intermediate vertices, modify it; Otherwise, maintain the original value. All vertex probes are completed and the algorithm ends.
//Freudian algorithm
#include <iostream>
using namespace std;
#define MaxInt 32767 // Represents the maximum value, i.e. ∞
#define MVNum 100 // max vertex
typedef char VerTexType; //Assume that the data type of the vertex is character type
typedef int ArcType; //It is assumed that the weight type of the edge is integer
int Path[MVNum][MVNum]; //The sequence number of the previous vertex vj of the vertex on the shortest path
int D[MVNum][MVNum]; //Record the shortest path length between vertices vi and vj
//------------Adjacency matrix of graph---------------
typedef struct{
VerTexType vexs[MVNum]; //Vertex table
ArcType arcs[MVNum][MVNum]; //adjacency matrix
int vexnum,arcnum; //Current number of points and edges of a graph
}AMGraph;
int LocateVex(AMGraph G , VerTexType v){
//Determine the position of point v in G
for(int i = 0; i < G.vexnum; ++i)
if(G.vexs[i] == v)
return i;
return -1;
}//LocateVex
void CreateUDN(AMGraph &G){
//The adjacency matrix representation is used to create the directed network G
int i , j , k;
cout <<"Please enter the total number of vertices and sides, separated by spaces:";
cin >> G.vexnum >> G.arcnum; //Enter the total number of vertices and edges
cout << endl;
cout << "Enter a name for the point, such as a" << endl;
for(i = 0; i < G.vexnum; ++i){
cout << "Please enter page" << (i+1) << "Name of the first point:";
cin >> G.vexs[i]; //Enter the information of the points in turn
}
cout << endl;
for(i = 0; i < G.vexnum; ++i){ //Initialize the adjacency matrix, and set the weights of the edges to the maximum MaxInt
for(j = 0; j < G.vexnum; ++j){
if(j != i)
G.arcs[i][j] = MaxInt;
else
G.arcs[i][j] = 0;
}//for
}//for
cout << "Enter the vertex and weight of the edge, such as a b 3" << endl;
for(k = 0; k < G.arcnum;++k){ //Construct adjacency matrix
VerTexType v1 , v2;
ArcType w;
cout << "Please enter page" << (k + 1) << "Vertex and weight of edge attachment:";
cin >> v1 >> v2 >> w; //Enter the vertex and weight of an edge
i = LocateVex(G, v1); j = LocateVex(G, v2); //Determine the position of v1 and v2 in G, that is, the subscript of the vertex group
G.arcs[i][j] = w; //The weight of edge < V1, V2 > is set to w
}//for
}//CreateUDN
void ShortestPath_Floyed(AMGraph G){
//Using Floyd algorithm to find the shortest path between each pair of vertices i and j in directed network G
int i , j , k ;
for (i = 0; i < G.vexnum; ++i) //Initial known path and distance between pairs of nodes
for(j = 0; j < G.vexnum; ++j){
D[i][j] = G.arcs[i][j];
if(D[i][j] < MaxInt && i != j) Path[i][j]=i; //If there is an arc between i and j, set the precursor of J to i
else Path [i][j] = -1; //If there is no arc between i and j, set the precursor of J to - 1
}//for
for(k = 0; k < G.vexnum; ++k)
for(i = 0; i < G.vexnum; ++i)
for(j = 0; j < G.vexnum; ++j)
if(D[i][k] + D[k][j] < D[i][j]){ //The path from i through k to j is shorter
D[i][j] = D[i][k]+D[k][j]; //Update D[i][j]
Path[i][j] = Path[k][j]; //Change the precursor of j to k
}//if
}//ShortestPath_Floyed
void DisplayPath(AMGraph G , int begin ,int temp ){
//Show shortest path
if(Path[begin][temp] != -1){
DisplayPath(G , begin ,Path[begin][temp]);
cout << G.vexs[Path[begin][temp]] << "-->";
}
}//DisplayPath
void main(){
cout << "************Freudian algorithm**************" << endl << endl;
AMGraph G;
char start , destination;
int num_start , num_destination;
CreateUDN(G);
cout <<endl;
cout << "Directed net G Creation completed!" << endl;
ShortestPath_Floyed(G);
cout << "Please enter the names of the starting point and the ending point of the path in sequence:";
cin >> start >> destination;
num_start = LocateVex(G , start);
num_destination = LocateVex(G , destination);
DisplayPath(G , num_start , num_destination);
cout << G.vexs[num_destination] << endl;
cout << "The shortest path length is:" << D[num_start][num_destination] << endl;
cout <<endl;
}//main
③. Topological sorting
For a project, we are most concerned about two issues:
- Whether the project can be successfully completed; (topological sorting)
- The minimum period of work necessary for the completion of the whole project. (critical path)
Directed acyclic graph ---- directed acyclic graph, referred to as DAG graph
AOV network: a directed graph is used to represent the subprojects of a project and their mutual restriction relationship, in which the vertex represents the activity and the arc represents the priority restriction relationship between activities. This directed graph is called the network in which the vertex represents the activity, which is referred to as AOV network for short.
AOV network should be a directed acyclic graph, namely DAG graph.
Topology sorting:
That is to arrange all vertices in the AOV network into a linear sequence (called topological sequence), which satisfies:
If there is a path from vertex vi to vj in AOV network, vertex vi in the linear sequence must precede vj
- Select a vertex without precursor in the directed graph and output it (i.e. the degree of penetration is 0)
- Deletes the vertex and all edges starting from it from the graph
- Repeat (1) (2) until there are no vertices without precursors
- If the number of vertices output at this time is less than that of the directed graph, it indicates that there are rings in the directed graph, otherwise the output vertex sequence is a topological sequence

Topology sorting implementation
-
Calculate the in degree of a vertex, store it in the array indegree[i], and stack the vertices with 0 in degree.
-
As long as the stack is not empty, repeat the following operations
-The vertex vi at the top of the stack is out of the stack and saved in the topology sequence array topo;
-For each adjacent point of vertex vi, the depth of vk is reduced by 1. If the depth of vk becomes 0, vk is put on the stack -
If the number of output vertices is less than the number of vertices of AOV network, there is a directed ring in the web address and topological sorting cannot be carried out. Otherwise, topological sorting is successful.
//Topological sorting
#include <iostream>
using namespace std;
#define MVNum 100 // max vertex
#define OK 1
#define ERROR 0
typedef char VerTexType;
//----- adjacency table storage representation of graph -----
typedef struct ArcNode{ //Edge node
int adjvex; //The position of the vertex that the edge points to
struct ArcNode *nextarc; //Pointer to the next edge
}ArcNode;
typedef struct VNode{
VerTexType data; //Vertex information
ArcNode *firstarc; //Pointer to the first edge attached to the vertex
}VNode, AdjList[MVNum]; //AdjList indicates the adjacency table type
typedef struct{
AdjList vertices; //Adjacency table
AdjList converse_vertices; //Inverse adjacency table
int vexnum, arcnum; //The current number of vertices and edges of a graph
}ALGraph;
//- - - - - - - - - - - - - - - -
//----- definition of sequential stack -----
typedef struct{
int *base;
int *top;
int stacksize;
}spStack;
//- - - - - - - - - - - - - - - -
int indegree[MVNum]; //The array indegree stores the penetration of a vertex
spStack S;
//------------Stack related operations----------------------
void InitStack(spStack &S){
//Initialization stack
S.base = new int[MVNum];
if(!S.base)
exit(1);
S.top = S.base;
S.stacksize = MVNum;
}//InitStack
void Push(spStack &S , int i){
//Enter the stack
if(S.top - S.base == S.stacksize)
return;
*S.top++ = i;
}//Push
void Pop(spStack &S , int &i){
//Out of stack
if(S.top == S.base)
return;
i = *--S.top;
}//Pop
bool StackEmpty(spStack S){
//Determine whether the stack is empty
if(S.top == S.base)
return true;
return false;
}//StackEmpty
//-------------------------------------------------
int LocateVex(ALGraph G , VerTexType v){
//Determine the position of point v in G
for(int i = 0; i < G.vexnum; ++i)
if(G.vertices[i].data == v)
return i;
return -1;
}//LocateVex
int CreateUDG(ALGraph &G){
//Create adjacency table and inverse adjacency table of directed graph G
int i , k;
cout <<"Please enter the total number of vertices and sides, separated by spaces:";
cin >> G.vexnum >> G.arcnum; //Enter the total number of vertices and edges
cout << endl;
cout << "Enter a name for the point, such as a" << endl;
for(i = 0; i < G.vexnum; ++i){ //Input each point to construct the header node table
cout << "Please enter page" << (i+1) << "Name of the first point:";
cin >> G.vertices[i].data; //Enter vertex value
G.converse_vertices[i].data = G.vertices[i].data;
//The pointer field of the initialization header node is NULL
G.vertices[i].firstarc=NULL;
G.converse_vertices[i].firstarc=NULL;
}//for
cout << endl;
cout << "Enter the vertex to which the edge is attached, such as a b" << endl;
for(k = 0; k < G.arcnum;++k){ //Input each edge to construct the adjacency table
VerTexType v1 , v2;
int i , j;
cout << "Please enter page" << (k + 1) << "Vertex to which an edge is attached:";
cin >> v1 >> v2; //Enter the two vertices to which an edge is attached
i = LocateVex(G, v1); j = LocateVex(G, v2);
//Determine the position of v1 and v2 in G, that is, the sequence number of vertices in G.vertices
ArcNode *p1=new ArcNode; //Generate a new edge node * p1
p1->adjvex=j; //The serial number of adjacent points is j
p1->nextarc = G.vertices[i].firstarc; G.vertices[i].firstarc=p1;
//Insert the new node * p1 into the edge table header of vertex vi
ArcNode *p2=new ArcNode; //Generate a new edge node * p1
p2->adjvex=i; //The serial number of the inverse adjacent contact is i
p2->nextarc = G.converse_vertices[j].firstarc; G.converse_vertices[j].firstarc=p2;
//Insert the new node * p1 into the edge table header of vertex vi
}//for
return OK;
}//CreateUDG
void FindInDegree(ALGraph G){
//Calculate the penetration of each vertex and store it in the array indegree
int i , count;
for(i = 0 ; i < G.vexnum ; i++){
count = 0;
ArcNode *p = G.converse_vertices[i].firstarc;
if(p){
while(p){
p = p->nextarc;
count++;
}
}
indegree[i] = count;
}
}//FindInDegree
int TopologicalSort(ALGraph G , int topo[]){
//Directed graph G adopts adjacency table storage structure
//If G has no loop, generate a topological sequence topo [] of G and return OK, otherwise ERROR
int i , m;
FindInDegree(G); //Calculate the penetration of each vertex and store it in the array indegree
InitStack(S); //Stack S initialized to empty
for(i = 0; i < G.vexnum; ++i)
if(!indegree[i]) Push(S, i); //If the entry degree is 0, enter the stack
m = 0; //The initial count of vertices is 0
while(!StackEmpty(S)){ //Stack S is not empty
Pop(S, i); //Push the top of the stack vi out of the stack
topo[m]=i; //Save vi in topology sequence array topo
++m; //Count output vertices
ArcNode *p = G.vertices[i].firstarc; //p points to the first adjacent contact of vi
while(p){
int k = p->adjvex; //vk is the adjacency point of vi
--indegree[k]; //The penetration of each adjacent point of vi minus 1
if(indegree[k] ==0) Push(S, k); //If the input degree is reduced to 0, it will be put into the stack
p = p->nextarc; //p points to the next adjacent node of vertex vi
}//while
}//while
if(m < G.vexnum) return ERROR; //The directed graph has a loop
else return OK;
}//TopologicalSort
int main(){
cout << "************Topological sorting**************" << endl << endl;
ALGraph G;
CreateUDG(G);
int *topo = new int [G.vexnum];
cout << endl;
cout << "The adjacency table and inverse adjacency table of directed graph are created!" << endl << endl;
if(TopologicalSort(G , topo)){
cout << "The topological ordered sequence of the directed graph is:";
for(int j = 0 ; j < G.vexnum; j++){
if(j != G.vexnum - 1)
cout << G.vertices[topo[j]].data << " , ";
else
cout << G.vertices[topo[j]].data << endl << endl;
}//for
}
else
cout << "There are rings in the network, unable to sort topology!" <<endl << endl;
return OK;
}//main
④. critical path
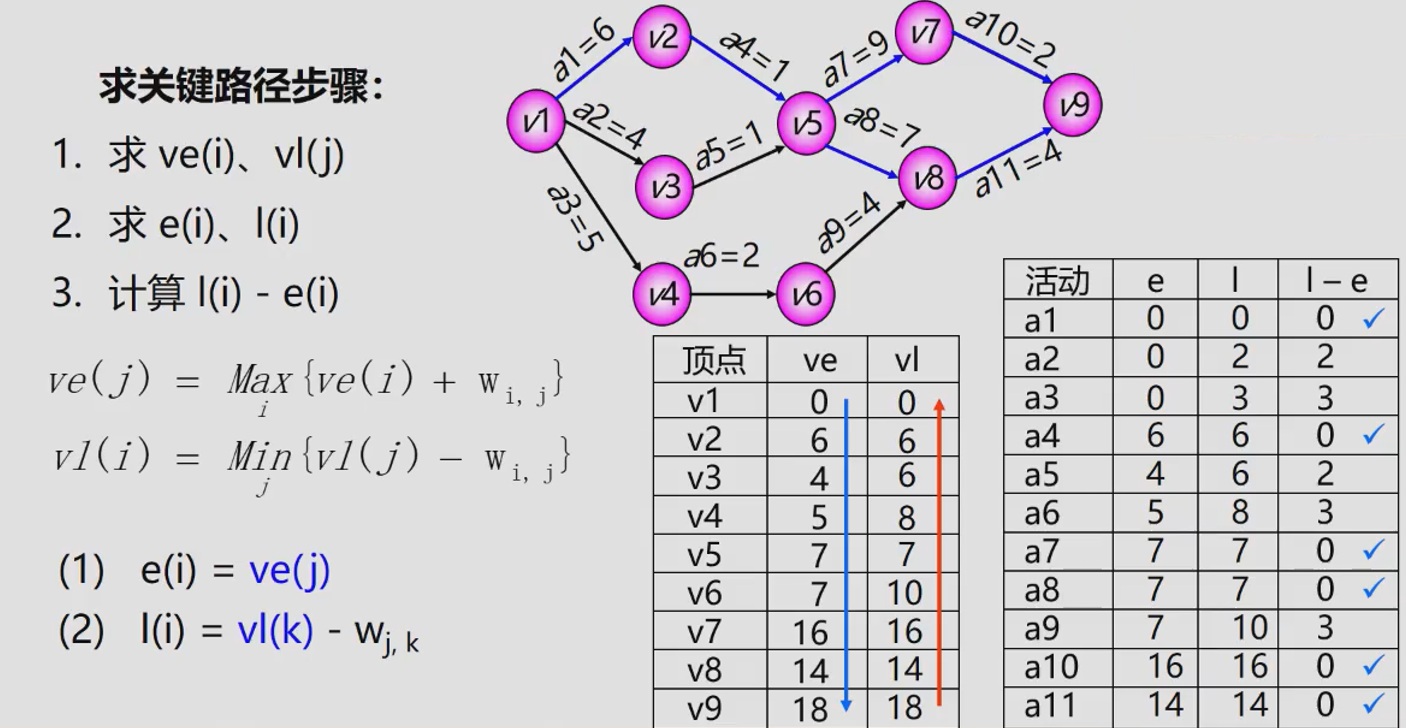
AOE network (Activity On Edges) - a network with edges representing activities, a directed graph representing the sub projects of a project and their mutual constraints, an arc representing activities, a weight representing the duration of activities, and a vertex representing events (start or end time of activities). This kind of directed graph is called a network with edges representing activities, which is called AOE network for short; AOE network is used to estimate the completion time of the project.
| name | explain |
|---|---|
| Source point | Vertices with 0 penetration (only 1) |
| Meeting point | Vertices with degree 0 (only 1) |
| path length | Sum of duration of each activity on the path |
| Completion time of the whole project | The longest path from the source point to the sink point of a directed graph |
| critical path | The path with the longest path length |
| Key activities | For the activities on the critical path, the increase of the weight on the edge will increase the length of the longest path on the directed graph. |
| ve(j) | Indicates the earliest occurrence time of event V |
| vl(j) | Indicates the latest occurrence time of event V |
| e(i) | Indicates the earliest start time of the activity ai |
| l(i) | Indicates the latest start time of the activity ai |
| l(i)-e(i) | Indicates the time allowance to complete the activity ai |
Note: in an AOE network, there can be more than one critical path.
critical path

//Critical path algorithm
#include <iostream>
using namespace std;
#define MVNum 100 // max vertex
#define BDNum MVNum * (MVNum - 1) // Maximum number of sides
#define OK 1
#define ERROR 0
typedef char VerTexType;
//----- adjacency table storage representation of graph -----
typedef struct ArcNode{ //Edge node
int adjvex; //The position of the vertex that the edge points to
int weight; //Weight
struct ArcNode *nextarc; //Pointer to the next edge
}ArcNode;
typedef struct VNode{
VerTexType data; //Vertex information
ArcNode *firstarc; //Pointer to the first edge attached to the vertex
}VNode, AdjList[MVNum]; //AdjList indicates the adjacency table type
typedef struct{
AdjList vertices; //Adjacency table
AdjList converse_vertices; //Inverse adjacency table
int vexnum, arcnum; //The current number of vertices and edges of a graph
}ALGraph;
//- - - - - - - - - - - - - - - -
//----- definition of sequential stack -----
typedef struct{
int *base;
int *top;
int stacksize;
}spStack;
//- - - - - - - - - - - - - - - -
int indegree[MVNum]; //The array indegree stores the penetration of a vertex
int ve[BDNum]; //Earliest occurrence time of event vi
int vl[BDNum]; //Latest occurrence time of event vi
int topo[MVNum]; //Record the vertex sequence number of the topology sequence
spStack S;
//----------------Stack operation--------------------
void InitStack(spStack &S){
//Initialization of stack
S.base = new int[MVNum];
if(!S.base)
exit(1);
S.top = S.base;
S.stacksize = MVNum;
}//InitStack
void Push(spStack &S , int i){
//Push
if(S.top - S.base == S.stacksize)
return;
*S.top++ = i;
}//Push
void Pop(spStack &S , int &i){
//Out of stack
if(S.top == S.base)
return;
i = *--S.top;
}//Pop
bool StackEmpty(spStack S){
//Determine whether the stack is empty
if(S.top == S.base)
return true;
return false;
}//StackEmpty
//---------------------------------------
int LocateVex(ALGraph G , VerTexType v){
//Determine the position of point v in G
for(int i = 0; i < G.vexnum; ++i)
if(G.vertices[i].data == v)
return i;
return -1;
}//LocateVex
int CreateUDG(ALGraph &G){
//Create adjacency table and inverse adjacency table of directed graph G
int i , k;
cout <<"Please enter the total number of vertices and sides, separated by spaces:";
cin >> G.vexnum >> G.arcnum; //Enter the total number of vertices and edges
cout << endl;
cout << "Enter a name for the point, such as a" << endl;
for(i = 0; i < G.vexnum; ++i){ //Input each point to construct the header node table
cout << "Please enter page" << (i+1) << "Name of the first point:";
cin >> G.vertices[i].data; //Enter vertex value
G.converse_vertices[i].data = G.vertices[i].data;
//The pointer field of the initialization header node is NULL
G.vertices[i].firstarc=NULL;
G.converse_vertices[i].firstarc=NULL;
}//for
cout << endl;
cout << "Enter the vertex to which the edge is attached and its weight, such as a b 3" << endl;
for(k = 0; k < G.arcnum;++k){ //Input each edge to construct the adjacency table
VerTexType v1 , v2;
int i , j , w;
cout << "Please enter page" << (k + 1) << "Vertices attached to edges and their weights:";
cin >> v1 >> v2 >> w; //Enter the two vertices to which an edge is attached
i = LocateVex(G, v1); j = LocateVex(G, v2);
//Determine the position of v1 and v2 in G, that is, the sequence number of vertices in G.vertices
ArcNode *p1=new ArcNode; //Generate a new edge node * p1
p1->adjvex=j; //The serial number of adjacent points is j
p1->nextarc = G.vertices[i].firstarc; G.vertices[i].firstarc=p1;
p1->weight = w;
//Insert the new node * p1 into the edge table header of vertex vi
ArcNode *p2=new ArcNode; //Generate a new edge node * p1
p2->adjvex=i; //The serial number of the inverse adjacent contact is i
p2->nextarc = G.converse_vertices[j].firstarc; G.converse_vertices[j].firstarc=p2;
p2->weight = w;
//Insert the new node * p1 into the edge table header of vertex vi
}//for
return OK;
}//CreateUDG
void FindInDegree(ALGraph G){
//Calculate the penetration of each vertex and store it in the array indegree
int i , count;
for(i = 0 ; i < G.vexnum ; i++){
count = 0;
ArcNode *p = G.converse_vertices[i].firstarc;
if(p){
while(p){
p = p->nextarc;
count++;
}
}//if
indegree[i] = count;
}//for
}//FindInDegree
int TopologicalOrder(ALGraph G , int topo[]){
//Directed graph G adopts adjacency table storage structure
//If G has no loop, generate a topological sequence topo [] of G and return OK, otherwise ERROR
int i , m;
FindInDegree(G); //Calculate the penetration of each vertex and store it in the array indegree
InitStack(S); //Stack S initialized to empty
for(i = 0; i < G.vexnum; ++i)
if(!indegree[i]) Push(S, i); //If the entry degree is 0, enter the stack
m = 0; //Count the output vertices, initially 0
while(!StackEmpty(S)){ //Stack S is not empty
Pop(S, i); //Push the top of the stack vi out of the stack
topo[m]=i; //Save vi in topology sequence array topo
++m; //Count output vertices
ArcNode *p = G.vertices[i].firstarc; //p points to the first adjacent contact of vi
while(p){
int k = p->adjvex; //vk is the adjacency point of vi
--indegree[k]; //The penetration of each adjacent point of vi minus 1
if(indegree[k] ==0) Push(S, k); //If the input degree is reduced to 0, it will be put into the stack
p = p->nextarc; //p points to the next adjacent node of vertex vi
}//while
}//while
if(m < G.vexnum) return ERROR; //The directed graph has a loop
else return OK;
}//TopologicalOrder
int CriticalPath(ALGraph G){
//G is the directed network stored in the adjacency table and outputs the key activities of G
int n , i , k , j , e , l;
if (!TopologicalOrder(G, topo)) return ERROR;
//Call the topology sorting algorithm to save the topology sequence in topo. If the call fails, there is a directed ring and ERROR is returned
n = G.vexnum; //n is the number of vertices
for(i = 0; i < n; i++) //Set the initial value of 0 for the earliest occurrence time of each event
ve[i] = 0;
/*――――――――――Find the earliest occurrence time of each event in topological order*/
for(i = 0;i < n; i++){
k = topo[i]; //Gets the vertex sequence number k in the topology sequence
ArcNode *p = G.vertices[k].firstarc; //p points to the first adjacent vertex of k
while(p != NULL){ //Update the earliest occurrence time of all adjacent vertices of k in turn
j = p->adjvex; //j is the sequence number of adjacent vertices
if(ve[j] < ve[k] + p->weight) //Earliest occurrence time of updating vertex j ve[j]
ve[j] = ve[k] + p->weight;
p = p->nextarc; //p points to the next adjacent vertex of k
} //while
} //for
for(i=0;i<n;i++) //Set the initial value ve[n-1] for the latest occurrence time of each event
vl[i]=ve[n-1];
/*――――――――――Calculate the latest occurrence time of each event in reverse topological order*/
for(i = n - 1;i >= 0; i--){
k = topo[i]; //Gets the vertex sequence number k in the topology sequence
ArcNode *p = G.vertices[k].firstarc; //p points to the first adjacent vertex of k
while(p != NULL){ //Update the latest occurrence time of k according to the adjacency point of k
j = p->adjvex; //j is the sequence number of adjacent vertices
if(vl[k] > vl[j] - p->weight) //Update the latest occurrence time of vertex K vl[k]
vl[k] = vl[j] - p->weight;
p = p->nextarc; //p points to the next adjacent vertex of k
}//while
}//for
/*――――――――――――Judge whether each activity is a key activity ――――――――――――*/
cout << endl;
cout << "The critical activity path is:";
for(i = 0;i < n; i++){ //vi is the start point for each activity
ArcNode *p = G.vertices[i].firstarc; //p points to the first adjacent vertex of i
while(p != NULL) {
j = p->adjvex; //j is the sequence number of adjacent vertices of i
e = ve[i]; //Calculate the earliest start time of the activity < VI, VJ >
l = vl[j] - p->weight; //Calculate the latest start time of the activity < VI, VJ >
if(e == l) //If it is a key activity, output < VI, VJ >
cout << G.vertices[i].data << "-->" << G.vertices[j].data << " ";
p = p->nextarc; //p points to the next adjacent vertex of i
} //while
} //for
return OK;
}//CriticalPath
int main(){
cout << "************Critical path algorithm**************" << endl << endl;
ALGraph G;
CreateUDG(G);
int *topo = new int [G.vexnum];
cout << endl;
cout << "Directed graph creation completed!" << endl << endl;
if(!CriticalPath(G))
cout << "There are rings in the network, unable to sort topology!" <<endl << endl;
cout << endl;
return OK;
}//main
Example:
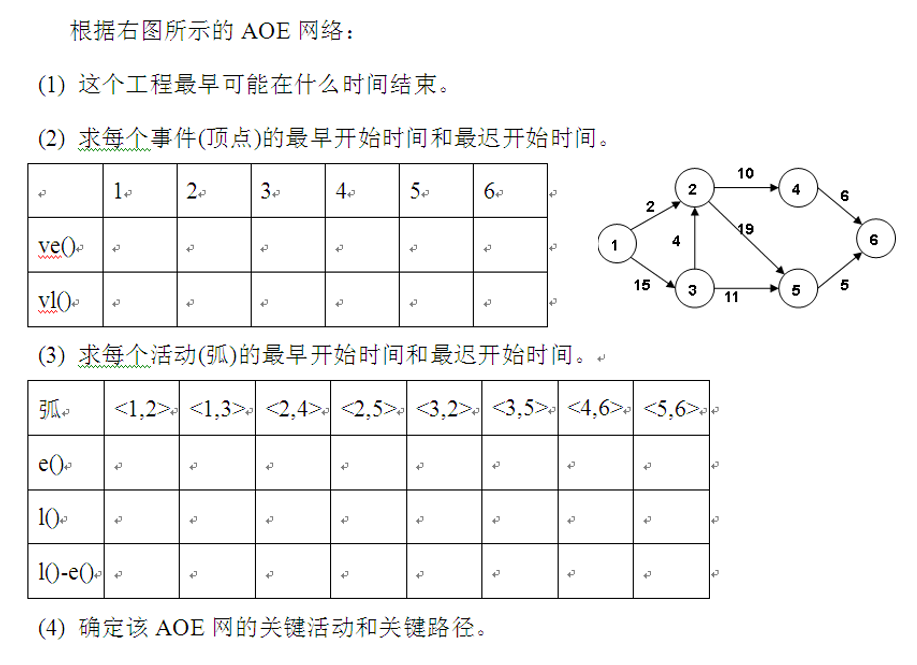
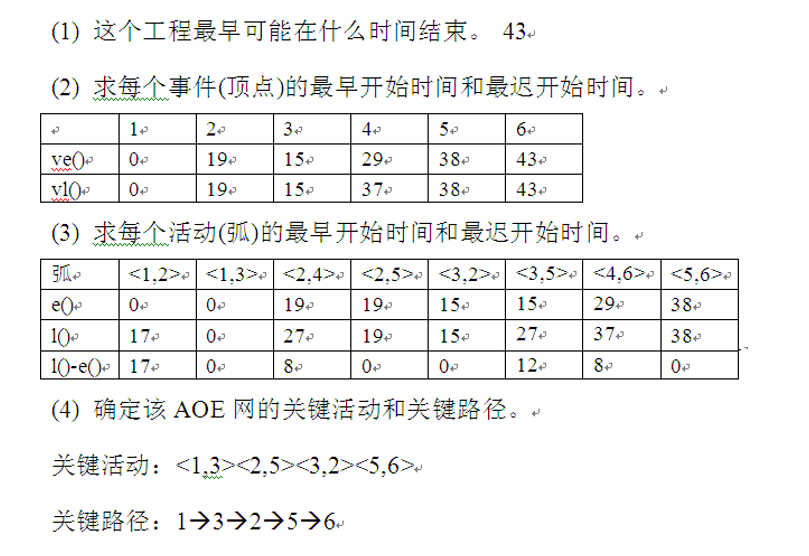
6. Summary
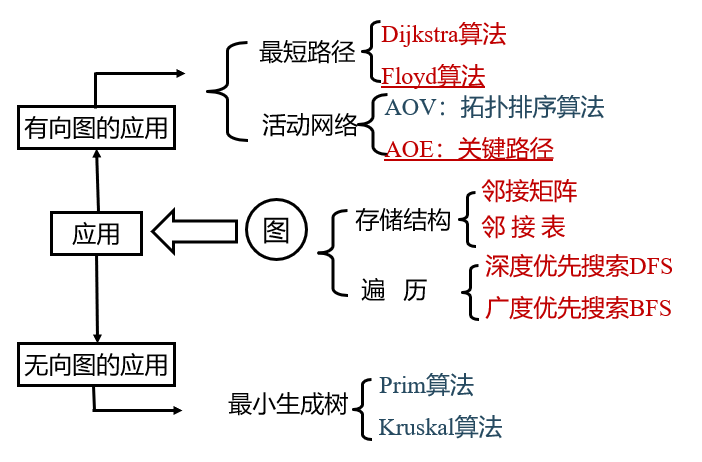
(1) According to different classification rules, graphs can be divided into many types: undirected graph, directed graph, complete graph, connected graph, strongly connected graph, weighted graph (Network), sparse graph and dense graph. Adjacency point, path, loop, degree, connected component and spanning tree are important terms commonly used in graph algorithm design.
(2) There are two kinds of storage methods of graphs: edge set representation and link representation. Among them, the adjacency matrix represented by edge set includes adjacency table, cross linked table and adjacency multiple table. Adjacency matrix representation is simple to realize by using two-dimensional array to represent the relationship between elements; Adjacency list, cross linked list and adjacency multiple list all belong to chain storage structure, which is more complex to implement. The specific storage representation in practical application can be selected according to the type of graph and the basic idea of actual algorithm. Adjacency matrix and adjacency table are two common storage structures. The comparison between them is shown in the figure below.
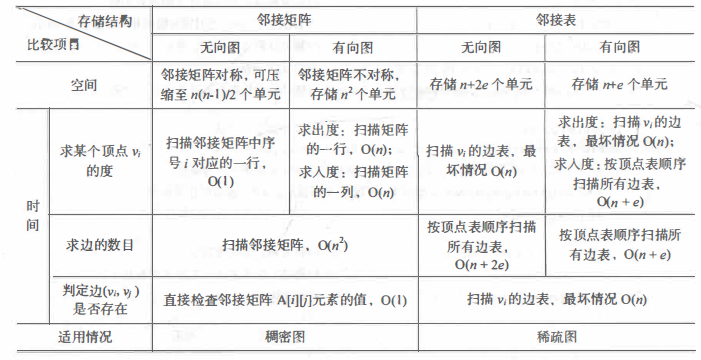
(3) graph traversal algorithm is the basis of realizing other operations of graph. There are two traversal methods of * * graph: depth first search traversal and breadth first search traversal** The depth first search traversal is similar to the pre order traversal of the tree, which is realized by means of the stack structure (recursion); Breadth first search traversal is similar to the hierarchical traversal of tree, which is realized by means of queue structure. The only difference between the two traversal methods is that the order of accessing vertices is different, so the time complexity is the same. When the adjacency matrix is used for storage, the time complexity is O(n2), and when the adjacency table is used for storage, the time complexity is O(n+e).
(4) Many algorithms of graph are closely related to practical applications. The commonly used algorithms include constructing the minimum spanning tree algorithm, solving the shortest path algorithm, topological sorting and solving the critical path algorithm.
① There are prim algorithm and Kruskal algorithm to construct the minimum spanning tree, both of which can achieve the same purpose. However, the core of the former algorithm is the merging point, and the time complexity is O(n2), which is suitable for dense networks; The latter is the merging edge, and the time complexity is O(elog2e), which is suitable for sparse networks.
② Shortest path algorithm: one is dijestra algorithm, which finds the shortest path from a source point to other vertices. The solution process is to generate the shortest path in the order of increasing path length, and the time complexity is O(n2); The other is the Freudian algorithm, which finds the shortest path between each pair of vertices, and the time complexity is O(n3). In terms of implementation form, this algorithm is more concise than calling dijestra algorithm n times with each vertex in the graph as the source point.
③ Topological sorting and critical path are the applications of directed acyclic graph. Topological sorting is based on a directed graph with vertices representing activities, that is, AOV network. For a directed graph without a ring, all vertices in the graph must be arranged into a linear sequence, that is, a topological sequence, which is not unique. The graph is represented by adjacency table, and the time complexity of topological sorting is O(n+e).
④ The critical path algorithm is based on a directed graph with arcs representing activities, that is, AOE network. The activities on the critical path are called critical activities. These activities are the key to affect the project progress. Their advance or delay will advance or delay the whole project. The critical path is not unique. The implementation of critical path algorithm is based on topological sorting, and the graph is represented by adjacency table. The time complexity of critical path algorithm is O(n+e).
7. Examples and Applications


- The following functions are realized by programming:
(1) The number of vertices, edges and vertex pairs of each edge of an undirected graph are input, and an undirected graph represented by adjacency matrix is established.
(2) The graph is traversed by depth first search and breadth first search, and its traversal sequence is output respectively.
Test sample undirected graph
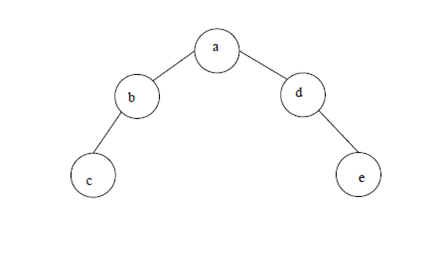
Operation results
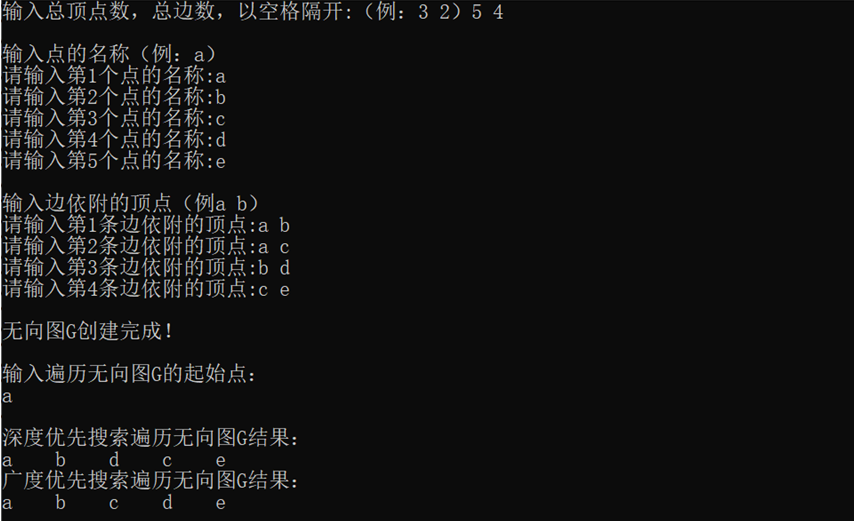
#include <bits/stdc++.h>
using namespace std;
#define MVNum 100
#define MAXQSIZE 100
typedef char VerTexType;
typedef int ArcType;
//Storage representation of adjacency matrix of graph
typedef struct
{
VerTexType vexs[MVNum];
ArcType arcs[MVNum][MVNum];
int vexnum, arcnum;
} Graph;
//Definition and operation of queue
typedef struct
{
ArcType *base;
int front;
int rear;
} sqQueue;
bool visited[MVNum];
bool visited1[MVNum];
int FirstAdjVex(Graph G, int v);
int NextAdjVex(Graph G, int v, int w);
//Build empty queue Q
void InitQueue(sqQueue &Q)
{
Q.base = new ArcType[MAXQSIZE];
if (!Q.base)
exit(1);
Q.front = Q.rear = 0;
}
//Insert a new tail element with element e as Q
void EnQueue(sqQueue &Q, ArcType e)
{
if ((Q.rear + 1) % MAXQSIZE == Q.front)
return;
Q.base[Q.rear] = e;
Q.rear = (Q.rear + 1) % MAXQSIZE;
}
//Determine whether it is an empty team
bool QueueEmpty(sqQueue Q)
{
if (Q.rear == Q.front)
return true;
return false;
}
//The team head element is out of the team and placed as u
void DeQueue(sqQueue &Q, ArcType &u)
{
u = Q.base[Q.front];
Q.front = (Q.front + 1) % MAXQSIZE;
}
//Determine the position of point v in G
int LocateVex(Graph G, VerTexType v)
{
for (int i = 0; i < G.vexnum; ++i)
if (G.vexs[i] == v)
return i;
return -1;
}
//The adjacency matrix representation is used to create undirected network G
void CreateUDN(Graph &G)
{
int i, j, k;
cout << "Enter the total number of vertices and sides, separated by spaces:(Example: 3 (2)";
cin >> G.vexnum >> G.arcnum;
cout << endl;
cout << "Enter the name of the point (example: a)" << endl;
for (i = 0; i < G.vexnum; ++i)
{
cout << "Please enter page" << (i + 1) << "Name of the first point:";
cin >> G.vexs[i];
}
cout << endl;
for (i = 0; i < G.vexnum; ++i)
for (j = 0; j < G.vexnum; ++j)
G.arcs[i][j] = 0;
cout << "Enter the vertex to which the edge is attached (example) a b)" << endl;
for (k = 0; k < G.arcnum; ++k)
{
VerTexType v1, v2;
cout << "Please enter page" << (k + 1) << "Vertex to which an edge is attached:";
cin >> v1 >> v2;
i = LocateVex(G, v1);
j = LocateVex(G, v2);
G.arcs[j][i] = G.arcs[i][j] = 1;
}
}
// DFS
void DFS(Graph G, int v)
{
int w;
cout << G.vexs[v] << " ";
visited[v] = true;
for (w = 0; w < G.vexnum; w++)
if ((G.arcs[v][w] != 0) && (!visited[w]))
DFS(G, w);
}
// BFS
void BFS(Graph G, int v)
{
sqQueue Q;
ArcType u;
ArcType w;
cout << G.vexs[v] << " ";
visited[v] = true;
InitQueue(Q);
EnQueue(Q, v);
while (!QueueEmpty(Q))
{
DeQueue(Q, u);
for (w = FirstAdjVex(G, u); w >= 0; w = NextAdjVex(G, u, w))
{
if (!visited[w])
{
cout << G.vexs[w] << " ";
visited[w] = true;
EnQueue(Q, w);
}
}
}
}
//Returns the first adjacent contact of v
int FirstAdjVex(Graph G, int v)
{
int i;
for (i = 0; i < G.vexnum; ++i)
{
if (G.arcs[v][i] == 1 && visited[i] == false)
return i;
}
return -1;
}
//Returns the next adjacent node of v relative to w
int NextAdjVex(Graph G, int v, int w)
{
int i;
for (i = w; i < G.vexnum; ++i)
{
if (G.arcs[v][i] == 1 && visited[i] == false)
return i;
}
return -1;
}
int main()
{
Graph G;
CreateUDN(G);
cout << endl;
cout << "Undirected graph G Creation completed!" << endl
<< endl;
cout << "Input traversal undirected graph G Starting point of:";
VerTexType c;
cin >> c;
int i;
for (i = 0; i < G.vexnum; ++i)
{
if (c == G.vexs[i])
break;
}
cout << endl;
while (i >= G.vexnum)
{
cout << "This point does not exist, please re-enter!" << endl;
cout << "Please enter the starting point of traversing the connected graph:";
cin >> c;
for (i = 0; i < G.vexnum; ++i)
{
if (c == G.vexs[i])
break;
}
}
cout << "Depth first search traversal undirected graph G result:" << endl;
DFS(G, i);
for (int j = 1; j <= G.vexnum; j++)
visited[j] = false;
cout << endl;
cout << "Breadth first search traversal undirected graph G result:" << endl;
BFS(G, i);
cout << endl;
return 0;
}