1. Basic concepts of search

Lookup table

A lookup table is a collection of data elements (or records) of the same type.

keyword

A keyword is the value of a data item in a data element (or record), which can be used to identify a data element (or record). If this keyword can uniquely identify a record, it is called the primary keyword (the primary keywords are different for different records). Conversely, the keywords used to identify several records are called sub keywords. When a data element has only one data item, its keyword is the value of the data element.

lookup

Lookup refers to determining a record or data element whose keyword is equal to the given value in the lookup table according to a given value. If there is such a record in the table, the search is successful. At this time, the search result can give the information of the whole record or indicate the position of the record in the search table; If there is no record with keyword equal to the given value in the table, the search is said to be unsuccessful. At this time, the search result can give a "null" record or a "null" pointer.

Dynamic lookup table and static lookup table

If you modify the table (such as insert and delete) while searching, the corresponding table is called dynamic lookup table, otherwise it is called static lookup table. In other words, the table structure of the dynamic lookup table itself is dynamically generated during the lookup process, that is, when the table is created, if there is a record in the table whose keyword is equal to the given value, the successful lookup will be returned; Otherwise, insert a record whose keyword is equal to the given value.

Average search length

In order to determine the position of the record in the lookup table, the expected value of the number of keywords that need to be compared with the given value is called the lookup algorithm, and the average lookup length when the lookup is successful. ( Average Search Length，ASL ).

2. Lookup of linear table

①. Sequential search

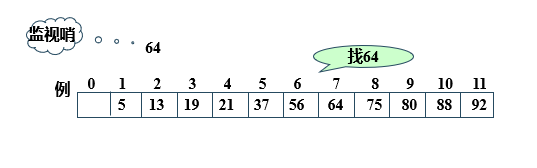
The search process of Sequential Search is: starting from one end of the table, compare the keyword of a record with the given value in turn. If the keyword of a record is equal to the given value, the search is successful; Conversely, if no record with the same keyword and given value is found after scanning the whole table, the search fails.

The sequential search method is suitable for both the sequential storage structure of linear table and the chain storage structure of linear table.

//Sequential search
#include<iostream>
using namespace std;
#define MAXSIZE 100
#define OK 1;

typedef struct{
	int key;//Keyword domain
}ElemType;

typedef struct{
	ElemType *R;
	int length;
}SSTable;

int InitList_SSTable(SSTable &L)
{
	L.R=new ElemType[MAXSIZE];
	if (!L.R)
	{
		cout<<"Initialization error";
		return 0;
	}
	L.length=0;
	return OK;
}

int Insert_SSTable(SSTable &L) 
{
	int j=0;
	for(int i=0;i<MAXSIZE;i++)
	{
		L.R[i].key=j;
		L.length++;
		j++;
	}
	return 1;
}

int Search_Seq(SSTable ST, int key){
    //In the sequence table ST, find the data elements whose keyword is equal to key in sequence. If found, the function value is
    //The position of the element in the table, otherwise it is 0
     for (int i=ST.length; i>=1; --i)  
             if (ST.R[i].key==key) return i;		//Look back and forward        
     return 0;
   }// Search_Seq

void Show_End(int result,int testkey)
{
	if(result==0)
		cout<<"not found"<<testkey<<endl;
	else
		cout<<"find"<<testkey<<"Location is"<<result<<endl;
	return;
}
void main()
{
	SSTable ST;
	InitList_SSTable(ST);
	Insert_SSTable(ST);
	int testkey1=7,testkey2=200;
	int result;
	result=Search_Seq(ST, testkey1);
	Show_End(result,testkey1);
	result=Search_Seq(ST, testkey2);
	Show_End(result,testkey2);
}

Improvement: store the keyword key to be checked into the header ("sentry") and compare it one by one from back to front, which eliminates the need to detect whether the search is completed at each step in the search process and speeds up the speed.

//Set the order of lookups
#include<iostream>
using namespace std;
#define MAXSIZE 100
#define OK 1;

typedef struct{
	int key;//Keyword domain
}ElemType;

typedef struct{
	ElemType *R;
	int length;
}SSTable;

int InitList_SSTable(SSTable &L)
{
	L.R=new ElemType[MAXSIZE];
	if (!L.R)
	{
		cout<<"Initialization error";
		return 0;
	}
	L.length=0;
	return OK;
}

int Insert_SSTable(SSTable &L) 
{
	int j=1;//Vacate the position of ST.R[0]
	for(int i=1;i<MAXSIZE;i++)
	{
		L.R[i].key=j;
		L.length++;
		j++;
	}
	return 1;
}

int Search_Seq(SSTable ST, int key){
      //In the sequence table ST, find the data elements whose keyword is equal to key in sequence. If found, the function value is
      //The position of the element in the table, otherwise it is 0
     ST.R[0].key = key;                          			//"Sentry"
     for(int i = ST.length; ST.R[i].key!=key; --i)  ;		//Look back and forward
     return i;                                         
}// Search_Seq
void Show_End(int result,int testkey)
{
	if(result==0)
		cout<<"not found"<<testkey<<endl;
	else
		cout<<"find"<<testkey<<"Location is"<<result<<endl;
	return;
}
void main()
{
	SSTable ST;
	InitList_SSTable(ST);
	Insert_SSTable(ST);
	int testkey1=7,testkey2=200;
	int result;
	result=Search_Seq(ST, testkey1);
	Show_End(result,testkey1);
	result=Search_Seq(ST, testkey2);
	Show_End(result,testkey2);
}

The time complexity of sequential search is O (n).

The advantages of sequential search are: the algorithm is simple and has no requirements for table structure. It is suitable for both sequential structure and chain structure. It can be applied whether the records are ordered according to keywords or not.

Its disadvantage is that the average search length is large and the search efficiency is low. Therefore, when n is large, sequential search is not used.

②. Half search

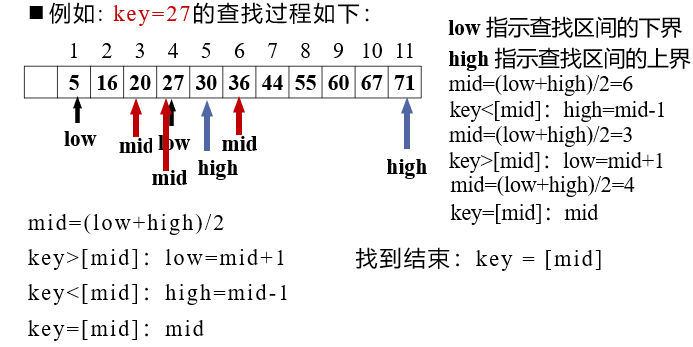
Binary Search, also known as Binary Search, is an efficient search method. However, the half search requires that the linear table must adopt the sequential storage structure, and the elements in the table are arranged in order by keywords (in order).

The search process of half search is: start from the intermediate record of the table. If the given value is equal to the keyword of the intermediate record, the search is successful; If the given value is greater than or less than the keyword of the intermediate record, search in the half of the table that is greater than or less than the intermediate record. Repeat the operation until the search is successful, or the search interval is empty in a step, which means the search fails.

Let the table length be n, low, high and mid respectively point to the upper bound, lower bound and midpoint of the interval where the element to be checked is located, and key is the value to be searched

1. Initially, let low = 1, high = n, mid = ⌊ (1ow+high)/2 ⌋
2. Compare the key with the record pointed to by the mid
   -If key = = R [mid] Key, search succeeded
   -If key < R [mid] Key, then high=mid-1
   -If key > R [mid] Key, then low=mid+1
3. Repeat the above operations until low > high, and the search fails

//Half search
#include<iostream>
using namespace std;
#define MAXSIZE 100
#define OK 1;

typedef struct{
	int key;//Keyword domain
}ElemType;

typedef struct{
	ElemType *R;
	int length;
}SSTable;

int InitList_SSTable(SSTable &L)
{
	L.R=new ElemType[MAXSIZE];
	if (!L.R)
	{
		cout<<"Initialization error";
		return 0;
	}
	L.length=0;
	return OK;
}

int Insert_SSTable(SSTable &L) 
{
	int j=1;
	for(int i=1;i<MAXSIZE;i++)
	{
		L.R[i].key=j;
		L.length++;
		j++;
	}
	return 1;
}

int Search_Bin(SSTable ST,int key) {
   // Find the data element whose keyword is equal to key in half in the ordered table ST. If found, the function value is
   // The position of the element in the table, otherwise it is 0
   int low=1,high=ST.length;							//Set initial value of search interval
   int  mid;
   while(low<=high) {
	   mid=(low+high) / 2;
      if (key==ST.R[mid].key)  return mid;      		//Find the element to be checked
      else if (key<ST.R[mid].key)  high = mid -1;		//Continue searching in the previous sub table
      else  low =mid +1;                       			//Continue searching in the next sub table
   }//while
   return 0;										//There is no element to be checked in the table
}// Search_Bin

void Show_End(int result,int testkey)
{
	if(result==0)
		cout<<"not found"<<testkey<<endl;
	else
		cout<<"find"<<testkey<<"Location is"<<result<<endl;
	return;
}

void main()
{
	SSTable ST;
	InitList_SSTable(ST);
	Insert_SSTable(ST);
	int testkey1=7,testkey2=200;
	int result;
	result=Search_Bin(ST, testkey1);
	Show_End(result,testkey1);
	result=Search_Bin(ST, testkey2);
	Show_End(result,testkey2);
}

The time complexity of half search is O(log2n). It can be seen that the efficiency of half search is higher than that of sequential search, but half search is only applicable to ordered tables and is limited to sequential storage structure.

The advantages of half search are: less comparison times and high search efficiency.

Its disadvantage is that it has high requirements for table structure and can only be used for ordered tables stored in sequence. Sorting is required before searching, and sorting itself is a time-consuming operation. At the same time, in order to maintain the order of the order table, when inserting and deleting the order table, the average comparison and moving half of the elements in the table is also a time-consuming operation. Therefore, half search is not suitable for linear tables with frequent changes in data elements.

③. Block search

1. Block order, that is, it is divided into several sub tables. It is required that the value in each sub table is smaller than that in the latter block (but the interior of the sub table may not be orderly).
2. Establish an "index table", which includes:
   -Keyword item: the largest keyword in each sub table.
   -Pointer item: indicates the starting address of the sub table.

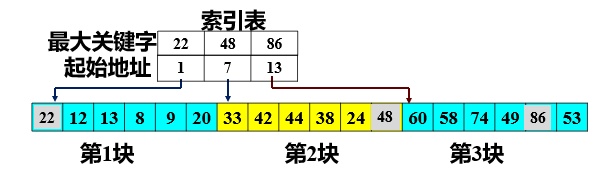
1. First determine the block where the record to be checked is located
   -Use the half search method for the index table (because the index table is an ordered table);
2. After determining the sub table where the keyword to be checked is located, the sequential search method is adopted in the sub table (because each sub table is an unordered table);

The advantage of block search is that when inserting and deleting data elements in the table, as long as the block corresponding to the element is found, the insertion and deletion operations can be carried out in the block. Due to the disorder in the block, it is easy to insert and delete without a lot of movement. If the linear table needs to be searched quickly and often changes dynamically, block search can be used.

Its disadvantage is to increase the storage space of an index table and sort the initial index table.

3. Tree table lookup

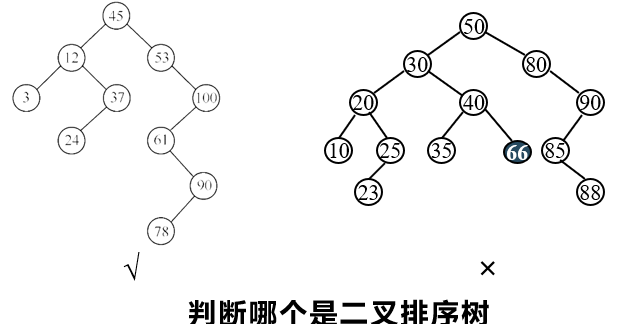
①. Binary sort tree

Binary Sort Tree, also known as binary search tree, is a special binary tree that is very useful for sorting and searching.

Definition of binary sort tree

Binary sort tree is either an empty tree or a binary tree with the following properties:

1. If its left subtree is not empty, the values of all nodes on the left subtree are less than the values of its root node;
2. If its right subtree is not empty, the value of all nodes on the right subtree is greater than that of its root node;
3. Its left and right subtrees are also binary sort trees.

Binary sort trees are recursively defined. From the definition, we can get an important property of binary sort tree: when traversing a binary tree in middle order, we can get an ordered sequence with increasing node values.

Binary tree sorting tree operation - find

1. If the binary sort tree is empty, the search fails and a null pointer is returned.
2. If the binary sort tree is not empty, match the given value key with the keyword T - > data of the root node Key for comparison:
   -If key = = t - > data Key, the search succeeds and the root node address is returned;
   -If keydata Key to further find the left subtree;
   -If key > T - > data Key to further find the right subtree.

Binary tree sorting tree operation - insert

1. If the binary sort tree is empty, the node * S to be inserted is inserted into the empty tree as the root node.
2. If the binary sort tree is not empty, the key and the keyword of the root node T > data Key for comparison:
   -If key is less than T - > data Key, then insert S into the left subtree;
   -If the key is greater than t > data, then insert S into the right subtree.

Binary tree sorting tree operation - create

1. Initialize binary sort tree T to an empty tree.
2. Read in a node whose keyword is key.
3. If the read keyword key is not the input end flag, the following operations are performed in a loop:
   -Insert this node into binary sort tree T;
   -Read a node whose keyword is key.

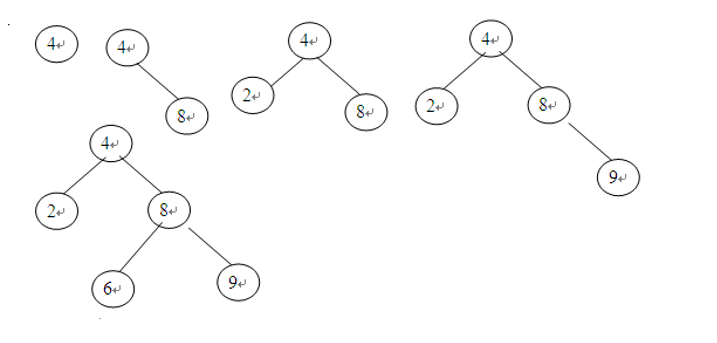
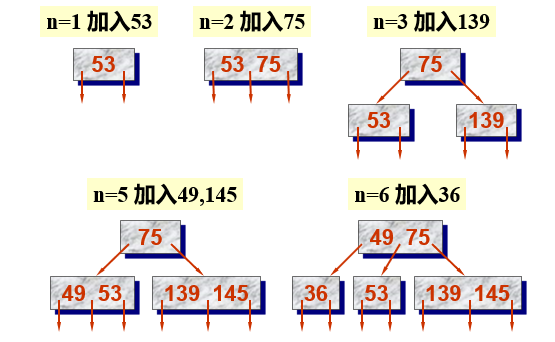
Example: set the input order of keywords as 45,24,53,45,12,24,90, and write out the creation process of binary sort tree.

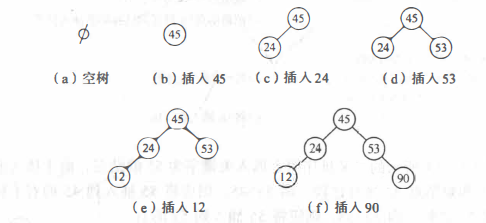
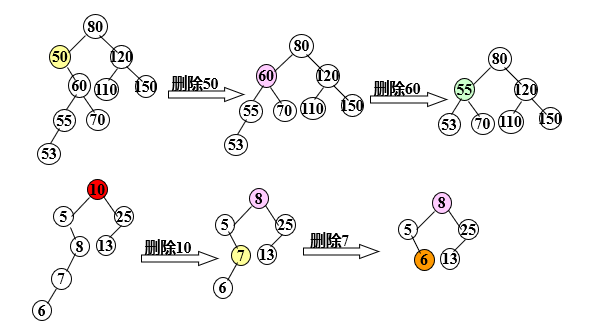
Binary tree sorting tree operation - delete

Principle: keep the middle order traversal order of all nodes unchanged after deletion
To delete a node, you cannot delete all subtrees with the node as the root, and re link the binary linked list broken due to the deletion of the node
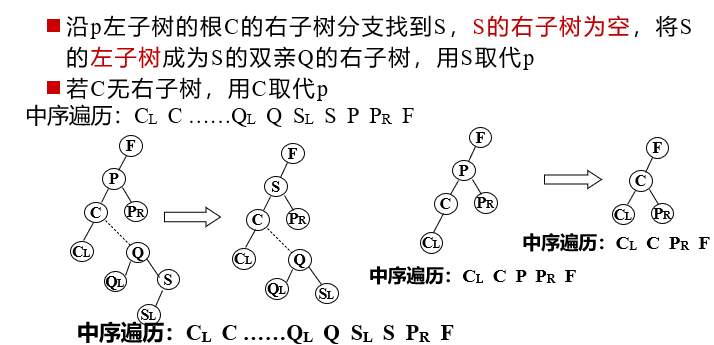
Suppose the deleted node is p (that is, the node pointed to by the P pointer), its parents are f, and P is the left child (or right child) of F. there are three cases:

1. The deleted node * p is a leaf node

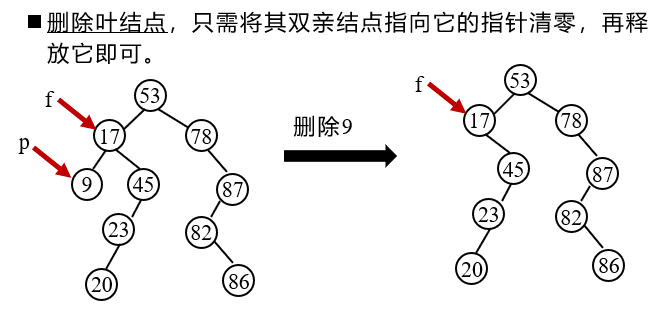
2. The deleted node * p has only left subtree or right subtree

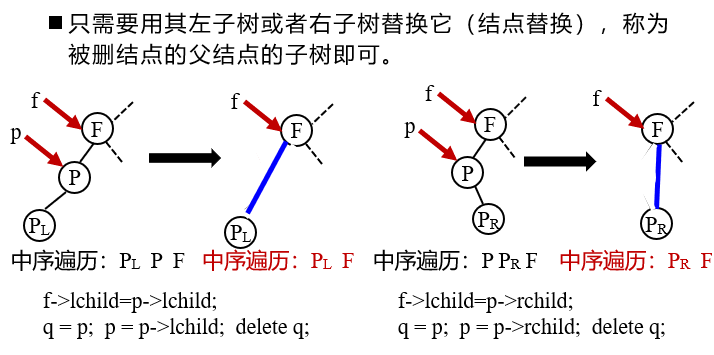
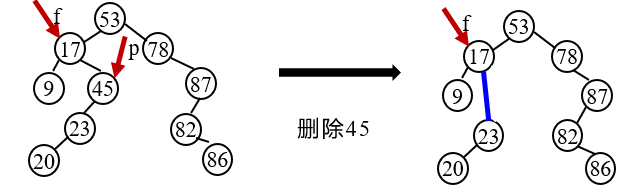
3. The deleted node * p has both left and right subtrees

//Comprehensive operation of binary sort tree
#include<iostream>
using namespace std;
#define ENDFLAG '#'
//char a[10]={'5','6','7','2','1','9','8','10','3','4','#'};// global variable
typedef struct ElemType{	
	char key;
}ElemType;

typedef struct BSTNode{
	ElemType data;	//Node data field
	BSTNode *lchild,*rchild;	//Left and right child pointers
}BSTNode,*BSTree;


//Recursive search of binary sort tree
BSTree SearchBST(BSTree T,char key) {
  //Recursively search for a data element with a keyword equal to key in the binary sort tree referred to by the root pointer T
  //If the search is successful, a pointer to the node of the data element is returned; otherwise, a null pointer is returned
  if((!T)|| key==T->data.key) return T;       	            	//Find end
  else if (key<T->data.key)  return SearchBST(T->lchild,key);	//Continue searching in the left subtree
  else return SearchBST(T->rchild,key);    		   			//Continue searching in the right subtree
} // SearchBST



//Insertion of binary sort tree
void InsertBST(BSTree &T,ElemType e ) {
  //When there is no data element with keyword equal to e.key in binary sort tree T, insert the element
  if(!T) {                				//Find the insertion position and the recursion ends
		 BSTree S = new BSTNode;            		//Generate new node * S
         S->data = e;                  		//The data field of the new node * S is set to e   
         S->lchild = S->rchild = NULL;	//New node * S as leaf node
         T =S;            				//Link the new node * S to the found insertion location
  }
  else if (e.key< T->data.key) 
      InsertBST(T->lchild, e );			//Insert * S into the left subtree
  else if (e.key> T->data.key) 
      InsertBST(T->rchild, e);			//Insert * S into right subtree
}// InsertBST



//Creation of binary sort tree
void CreateBST(BSTree &T ) {
  //Read in a node with the keyword key in turn and insert this node into the binary sort tree T
  T=NULL;
  ElemType e;
  cin>>e.key;        //???
  while(e.key!=ENDFLAG){   	//ENDFLAG is a user-defined constant, which is used as the input end flag
    InsertBST(T, e);          	//Insert this node into binary sort tree T
    cin>>e.key;			//???
  }//while            
}//CreatBST

void DeleteBST(BSTree &T,char key) {
  //Delete the node with keyword equal to key from binary sort tree T
  BSTree p=T;BSTree f=NULL;                     			//initialization
  BSTree q;
  BSTree s;
  /*------------The following while loop starts from the root to find the node * p whose keyword is equal to the key-------------*/
  while(p){                  
   if (p->data.key == key) break;  	      	//Find the node * p with keyword equal to key and end the cycle
   f=p;                                			//*f is the parent node of * p
   if (p->data.key> key)  p=p->lchild;     	//Continue searching in the left subtree of * p
   else p=p->rchild;  	                  		//Continue searching in the right subtree of * p
  }//while
if(!p) return;                         		//If the deleted node cannot be found, return
/*―Consider three situations to realize the internal processing of the subtree referred to by P: * p the left and right subtrees are not empty, there is no right subtree and no left subtree -*/
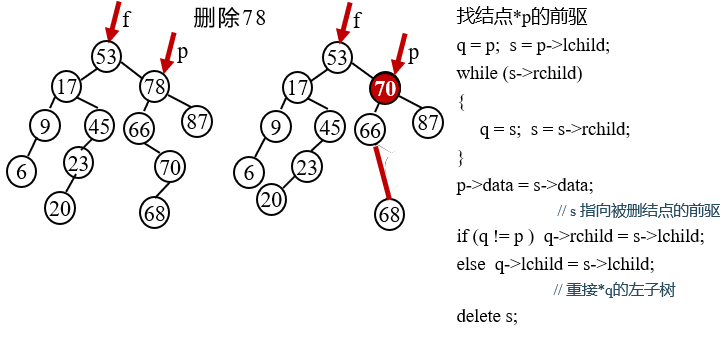
if ((p->lchild)&& (p->rchild)) {     		//Left and right subtrees of deleted node * p are not empty
     q = p;
	 s = p->lchild;
     while (s->rchild)                			//Continue to find its precursor node in the left subtree of * p, that is, the lowest right node
       {q = s; s = s->rchild;}	         		//Right to the end
     p->data = s->data;               			//s points to the "precursor" of the deleted node
     if(q!=p){
		 q->rchild = s->lchild;     	//Right subtree of reconnection * q
	 }
     else q->lchild = s->lchild;        		//Rejoin the left subtree of * q
     delete s;
  }//if
else{
	if(!p->rchild) {               		//The deleted node * p has no right subtree, and only needs to reconnect its left subtree
		  q = p; p = p->lchild; 
	  }//else if
	else if(!p->lchild) {               		//The deleted node * p has no left subtree, so you only need to reconnect its right subtree
		 q = p; p = p->rchild;
	  }//else if
	/*――――――――――Hang the subtree indicated by p to the corresponding position of its parent node * f ―――――――――*/
	  if(!f) T=p;                       			//The deleted node is the root node
	  else if (q==f->lchild) f->lchild = p;   	//Hanging to the left subtree of * f
	  else f->rchild = p;                 		//Hanging to the right subtree position of * f
	  delete q;
	}
}//DeleteBST

//Deletion of binary sort tree

//Middle order traversal
void InOrderTraverse(BSTree &T)
{
	if(T)
	{
	InOrderTraverse(T->lchild);
	cout<<T->data.key;
	InOrderTraverse(T->rchild);
	}
}

void main()
{
	BSTree T;
	cout<<"Please enter several characters to distinguish with carriage return#End input "< < endl";
	CreateBST(T);
	cout<<"The traversal result in the current ordered binary tree is"<<endl;
	InOrderTraverse(T);
	char key;//Content to be found or deleted
	cout<<"Please enter the character to be found"<<endl;
	cin>>key;
	BSTree result=SearchBST(T,key);
	if(result)
	{cout<<"Character found"<<key<<endl;}
	else
	{cout<<"not found"<<key<<endl;}
	cout<<"Please enter the characters to be deleted"<<endl;
	cin>>key;
	DeleteBST(T,key);
	cout<<"The traversal result in the current ordered binary tree is"<<endl;
	InOrderTraverse(T);
}

②. balanced binary tree

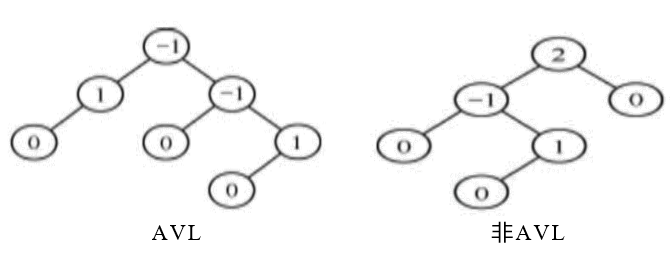
Balanced binary tree is also called AVL tree

• An AVL tree is either an empty tree or a binary sort tree with the following properties:
  -Its left subtree and right subtree are AVL trees, and the absolute value of the depth difference between the left subtree and right subtree is no more than 1.
  -The left and right subtrees are also AVL trees.

Add a number to each node to give the node balance factor BF.

BF: the difference between the left subtree depth and the right subtree depth of the node.

The balance factor of any node of AVL tree can only be - 1, 0, 1.

Balance adjustment method of balanced binary tree

If a new node is inserted into an AVL tree, it may cause imbalance. At this time, the structure of the tree must be readjusted to restore the balance.

Adjustment method: find the ancestor node closest to the insertion point and the absolute value of the balance factor exceeds 1. The subtree with this node as the root is called the minimum unbalanced subtree, which can limit the scope of rebalancing to this subtree.

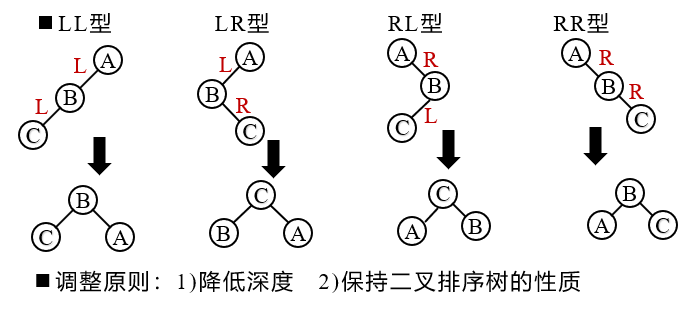
Insertion of balanced binary tree

When inserting a new node into an AVL tree, if the absolute value of the balance factor of a node in the tree | balance | > 1, there is an imbalance, which needs to be balanced.
Algorithm: start from an empty tree and gradually establish an AVL tree by inputting a series of keywords. When inserting new nodes, the balanced rotation method is used for balancing.

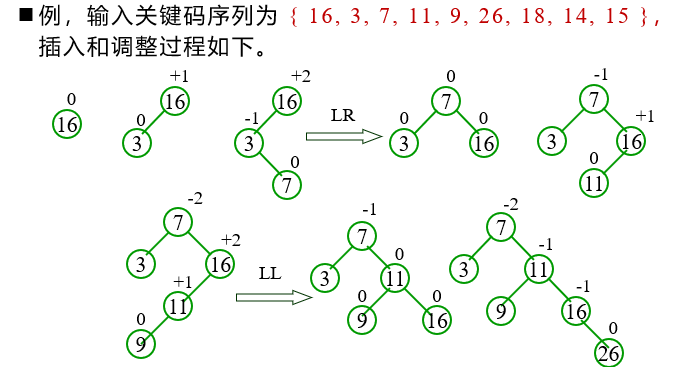
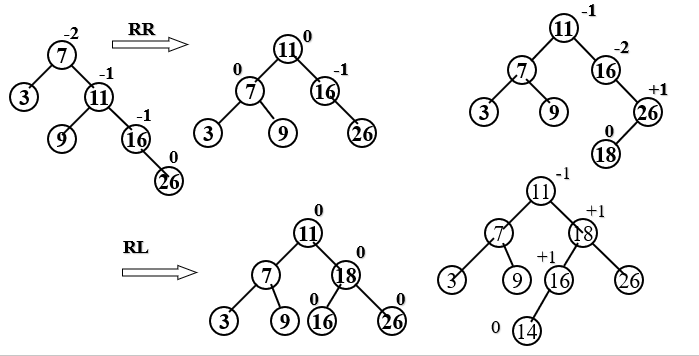
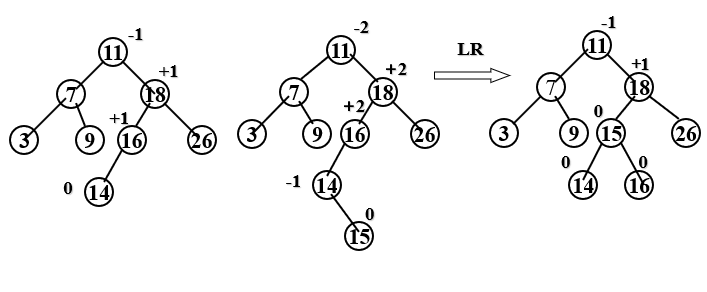
Example:

③. B-Trees

Concept of B-tree

B-tree was proposed by R.Bayer and E.Maccreight in 1970. It is a special multi fork tree. It is a dynamic index technology commonly used in external storage file system and an organizational structure of large database files. Each node in the B-tree has the same size.

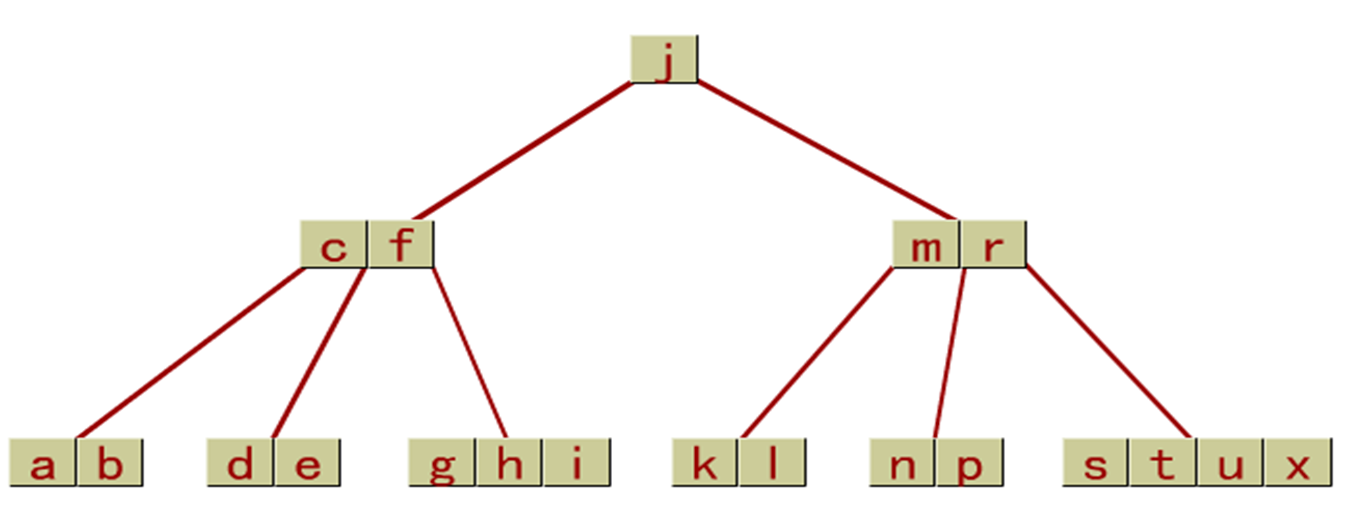
Node structure of B-tree

• M is called the order of B-tree, m ≥ 3
• par is the pointer field pointing to the parent node
• K1, K2,... Kn are n keywords in descending order
• For non root node ⌈ m/2 ⌉ - 1 ≤ n ≤ m-1
• P0, P1, P2,... Pn are n+1 pointers pointing to n+1 subtrees of the node respectively

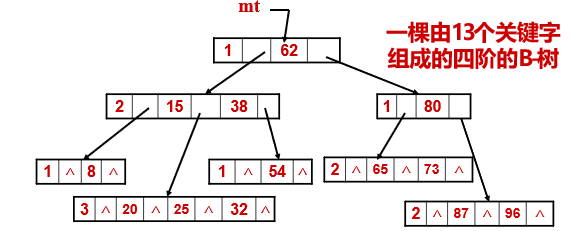
The keyword of each node is at least = ⌈ m/2 ⌉ - 1 = 2-1 = 1; Maximum = m-1=3, the minimum number of subtrees of each node is ⌈ m/2 ⌉ = 2, and the maximum is m=4. No matter how many keyword fields and pointer fields each node actually uses, it includes four keyword fields, four pointer fields pointing to the storage location of records, five pointer fields pointing to child nodes, one pointer field pointing to parent nodes and an n field storing the number of keywords.

Characteristics of B-tree

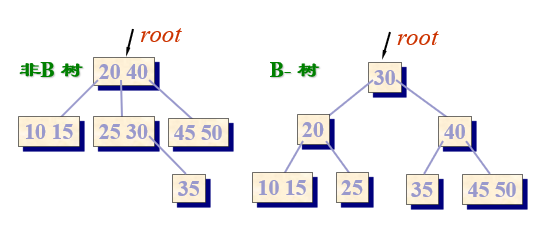
• An m-order B-tree (m-fork tree) is a balanced M-way search tree, which is either an empty tree or a tree satisfying the following properties:
  -The root node has at least 2 subtrees.
  -All nodes except the root node (excluding failed nodes) have at least ⌈ m/2 ⌉ subtrees.
  -All failed nodes (leaf nodes) are located on the same layer.
  -Each node can have up to m sub trees.
• The "failed" node in the B-tree is the node that can be reached when the search value x is not in the tree.
• If the insertion order of keywords is different, B-trees with different structures will be generated.
• A B-tree is a balanced m-way search tree, but a balanced m-way search tree is not necessarily a B-tree.

Search algorithm of B-tree

• The search process of B-tree is an alternating process of searching in nodes and searching down a certain path.
• The search time of B-tree is directly related to the order m of B-tree and the height h of B-tree, which must be weighed.
• When searching on B-tree, the time required for successful search depends on the level of key code; The time required for an unsuccessful search depends on the height of the tree.

Relationship between height h and number of keys N

If the number of nodes in each layer in the m-order B-tree reaches the minimum, the height of the B-tree may reach the maximum. Let the number of key codes in the tree be N. from the definition of B-tree, we know that there are at least 2 ⌈ m/2 ⌉ h-2 nodes in h-1 layer.

Selection of m value

If the order m of B-tree is increased, the height of the tree can be reduced, so as to reduce the number of reading nodes, so as to reduce the number of reading disks.
In fact, M is limited by the available space of memory. When m greatly exceeds the capacity of the memory workspace, the node cannot be read into the memory at one time, which increases the number of disk reading and the difficulty of searching in the node.
Selection of m value: the key shall be found in the B-tree × The total amount of time is minimized.
This time consists of two parts: the time spent reading nodes from disk + the time spent searching for x in nodes.

Insertion of B-tree

1. Search the record of the given keyword in the B-tree. If the search is successful, the insertion operation fails; Otherwise, the new record is inserted into the upper node (pointed by q) of the failed leaf node as an empty finger p.
2. If the number of keywords of the node pointed to by q does not exceed m-l after inserting the new record and null pointer, the inserting operation is successful, otherwise go to step ③.
3. Taking the ⌈ m/2 ⌉ keyword K ⌈ m/2 ⌉ of the node as the split point, the node is divided into three parts: the left part of K ⌈ m/2 ⌉ and the right part of K ⌈ m/2 ⌉. The left part of K ⌈ m/2 ⌉ remains in the original node; The right part of K ⌈ m/2 ⌉ is stored in a newly created node (pointed by p); The record and pointer p with the keyword value of K ⌈ m/2 ⌉ are inserted into the parent node of q. Since a new record is added to the parent node of q, the operations of ② and ③ must be repeated for the parent node of q, and so on until the node pointed by q is the root node, and then go to step ④.
4. ④ Since the root node has no parents, the pointers p and q of the two nodes generated by its splitting and the record with the keyword K ⌈ m/2 ⌉ form a new root node. At this time, the height of B - increases by 1.

B-tree deletion

When deleting a key in the B-tree, you first need to find the node where the key is located and delete the key from it.
If the node is not a leaf node and the deleted key is Ki;,1 ≤ i ≤ n, then after deleting the key, the node Pi shall be used; The smallest key in the indicated subtree × To replace the deleted key Ki; Where you are, and then × Delete the leaf x in the node.

//Search of B-tree
//Insertion of B-tree


#include<iostream>
using namespace std;
#define FALSE 0
#define TRUE 1
#define OK 1
#define m 3 						// The order of B-tree is temporarily set to 3
typedef struct BTNode{
	int keynum;					//The number of keywords in the node, that is, the size of the node
	BTNode *parent;				//Point to parent node
	int key[m+1];				//Keyword vector, unit 0 not used
	BTNode *ptr[m+1];			//Subtree pointer vector
}BTNode,*BTree;

//----- search result type definition of B-tree -----
struct Result{
  BTNode *pt;     							//Point to the node found
  int i;           							//1..m. Keyword sequence number in node
  int tag;         							//1: Lookup succeeded, 0: lookup failed
}; 	                           


int Search(BTree T,int key)
{
	BTree p=T;	
	int endnum;
	if(p)						//When the tree is not empty
	{
		endnum=p->keynum;		//Get the number of records contained in the first node
	}
	else
	{
		return 0;				//Return not found
	}
	int i=0;
	if(endnum==0)
	{
		return i;				//The tree exists, but there is only one empty root node
	}
	else if(key>=p->key[endnum])//The node is not empty, but the current value is larger than the maximum key
	{
		i=endnum;
		return i;
	}
	else if(key<=p->key[1])		//The node is not empty, but the current value is smaller than the smallest key
	{
		return i;}
	else
	{
		for(i=1;i<endnum;i++)	//There is a suitable position, that is, it is between the maximum and minimum values of the current node, or it is found
		{
			if(p->key[i]<=key && key<p->key[i+1])
				return i;
		}
	}
}

void Insert(BTree &q,int i,int x,BTree &ap)
{//Insert x into the i+1 position of the q node
	int j;
	for(j=m-1;j>i;j--)			
	{
		//Move all key s after the insertion position back one bit
		q->key[j+1]=q->key[j];
	}
	for(j=m;j>i;j--)
	{
		//Accordingly, the position of the subsequent ptr is also moved
		q->ptr[j]=q->ptr[j-1];
	}
	q->key[i+1]=x;//Insert x into this position
	q->ptr[i+1]=ap;
	q->keynum++;
}

void split(BTree &q,int s,BTree &ap)
{	//Move Q - > key [S + 1,.., M], q - > PTR [S + 1,.., M] into the new node * ap as the right node
	//The original node is the new left node
	//The intermediate value is saved in AP [0] - > key. Wait until it is found and jump back to InsertBTree() to find the appropriate insertion position
	int i;
	ap=new BTNode;
	for(i=s+1;i<=m;i++)
	{	//Save Q - > key [S + 1,.., M] to ap - > key [0,.., M-S + 1]
		//Save Q - > PTR [S + 1,.., M] to ap - > PTR [0,.., M-S + 1]
		ap->key[i-s-1]=q->key[i];	
		ap->ptr[i-s-1]=q->ptr[i];
	}
	if(ap->ptr[0])
	{
		//When ap has subtree
		for(i=0;i<=1;i++)
		{
			//Change the father of ap's subtree to ap itself
			ap->ptr[i]->parent=ap;
		}
	}
	ap->keynum=(m-s)-1;
	ap->parent=q->parent;//Change the father of ap to the father of q

	q->keynum=q->keynum-(m-s);//Number of records modified q
}

void NewRoot(BTree &T,BTree q,int x,BTree &ap)//Generate a new root node * t with information (T, x, ap), and the original T and ap are subtree pointers
{
	BTree newT=new BTNode;//Create a new node as the new root
	
	newT->key[1]=x;//Write key of new root [1]
	newT->ptr[0]=T;//Take the original tree root as the left subtree of the new root
	newT->ptr[1]=ap;//ap as the right subtree of the new root
	newT->keynum=1;
	newT->parent=NULL;//Xingen's father is empty

	ap->parent=newT;//ap's father is the new root
	T->parent=newT;//T's father is Xingen

	T=newT;//The tree is guided by a new root
}

//Insertion of B-tree
int InsertBTree(BTree &T,int K,BTree q,int i){
  int x=K;
  BTree ap=NULL;
  int finished=FALSE;//x represents the newly inserted keyword, and ap is a null pointer
  while(q&&!finished){
    Insert(q,i,x,ap);      		//Insert x and ap into Q - > key [i + 1] and Q - > PTR [i + 1], respectively
    if (q->keynum<m)
		finished=TRUE;   	//Insert complete
    else{                      	//Split node * q
     int s= m/2;
	 split(q,s,ap);
	x=ap->key[0];//	 x=q->key[s];
      //Move Q - > key [S + 1.. M], q - > PTR [s.. M] and Q - > recptr [S + 1.. M] into the new node * ap
      q=q->parent;
      if(q)
	  {
		  i=Search(q,x);
	  }		//Find the insertion position of x in the parent node * q
	}						//else
  }							//while
  if(!finished)    			//T is an empty tree (the initial value of parameter q is NULL) or the root node has been split into nodes * q and * ap
      NewRoot(T,q,x,ap);		//Generate a new root node * t with information (T, x, ap), and the original T and ap are subtree pointers
  return  OK;
}							//InsertBTree						//InsertBTree

//Search of B-tree
Result SearchBTree(BTree &T, int key){
	/*Search the keyword key on the m-order B-tree T and return the result (pt,i,tag). If the search is successful, the eigenvalue tag=1, and the ith keyword in the node pointed to by the pointer pt is equal to key; Otherwise, if the eigenvalue tag=0, the keyword equal to key should be inserted between the i and i+1 keywords in the node pointed to by the pointer pt*/
	BTree p=T;
	BTree q=NULL;
	int found=FALSE;
	int i=0;			//Initialization, p points to the node to be checked, and q points to p's parents
while(p&&!found){
    i=Search(p,key);               	
    //Find I in P - > key[1..keynum], so that: P - > key[i] < = key < p - > key[i+1]
    if(i>0&&p->key[i]==key)
		found=TRUE;		//Keywords to be checked found
    else
	{
		q=p;
		p=p->ptr[i];
	}
  }
	Result result;
if(found)
{
	result.pt=p;
	result.i=i;
	result.tag=1;
	return result;
}              		//Search succeeded
else
{
	result.pt=q;
	result.i=i;
	result.tag=0;
	return result;
}              			//If the search is unsuccessful, the insertion location information of K is returned
}//SearchBTree

void InitialBTree(BTree &T)
{
	//Initialize an empty root
	T->keynum=0;		
	T->parent=NULL;	
	for(int i=0;i<m+1;i++)
	{
		T->ptr[i]=NULL;
	}
}



void main()
{
	BTree T=new BTNode;
	InitialBTree(T);
	//First use SearchBTree() to find the position to insert and get a Result structure
	//Insert data with InsertBTree()
	Result result;
	int a[11]={45,24,53,90,3,12,50,61,70,100};
	for(int i=0;i<10;i++)
	{
		result=SearchBTree(T,a[i]);
		if(result.tag==0)
		{
			InsertBTree(T,a[i],result.pt,result.i);
		}
	}
	cout<<"OK";
}

④. B + tree

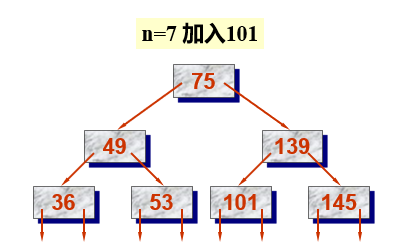
Definition of m-order B + tree

• Each non leaf node in the tree has at most m sub trees;
• The root node (non leaf node) has at least 2 subtrees. Except the root node, other non leaf nodes have at least ⌈ m/2 ⌉ subtrees;
• All leaf nodes are at the same level, including all key codes and pointers to the storage address of corresponding data objects, and the leaf nodes themselves are linked in the order of key codes from small to large.

• There are two header pointers in the B + tree: one pointing to the root node of the B + tree and the other pointing to the leaf node with the smallest key.

Two search operations can be performed on the B + tree:

Sequential search along leaf node chain
The other is the random search from the root node to the leaf node.
The process of random search, insertion and deletion on B + tree is basically similar to that of B-tree. Only in the search process, if the key on the non leaf node is equal to the given value, the search does not stop, but continues to look down along the right pointer until the key on the leaf node is found.

Search analysis of B + tree

The insertion of B + tree is only carried out on leaf nodes. After each (key pointer) index entry is inserted, it is necessary to judge whether the number of subtrees in the node is out of range.
When the number of subtrees in the inserted node is n > M1, the leaf node needs to be divided into two nodes, and their key codes are ⌈ (m1+1)/2 ⌉ and ⌊ (m1+1)/2 ⌋
Their parent nodes should contain the maximum key and node address of the two nodes at the same time. After that, the problem is attributed to the insertion in non leaf nodes.

Deletion of B + tree

Only on leaf nodes. When a (key pointer) index item is deleted on the leaf node, the number of subtrees in the node is still not less than ⌈ m1/2 ⌉ which belongs to simple deletion, and its upper index can not be changed.
If the deleted key is the minimum key of the node, but because the copy on the upper layer only acts as a "boundary key" to guide the search, the copy on the upper layer can still be retained.
If the number of subtrees n in a leaf node is less than the lower limit ⌈ m1/2 ⌉ of the number of subtrees after deleting a (key pointer) index entry in the leaf node, the nodes must be adjusted or merged.

If the number of subtrees of the right sibling node has reached the lower limit ⌈ m1/2 ⌉ and no redundant key can be moved into the node where the deleted key is located, the two nodes must be merged. Move all (key pointer) index entries in the right sibling node to the node where the deleted key is located, and then delete the right sibling node.
The merging of nodes will lead to the reduction of "boundary key" in parent nodes, which may be reduced to less than the lower limit of the number of subtrees in leaf nodes. This will cause adjustment or merging of non leaf nodes. If the last two children of the root node are merged, the number of layers of the tree will be reduced by one layer.

Difference between B-tree and B + tree

B-trees are divided into B-trees and B + trees, and their tree structures are roughly the same. The difference between a B + tree of order m and a B-tree is:

1. In B-tree, each node contains n keywords and n+1 subtrees, while in B + tree, each node contains n keywords and N subtrees;
2. In the B-tree, the value range of the number of keywords n in each node (except the root node) is: ⌈ m/2 ⌉ - 1 ≤ n ≤ m-1
   ; In the B + tree, the value range of the number of keywords n in each node (except the root node) is: ⌈ m/2 ⌉ ≤ n ≤ m, and the value range of the tree root node is: 1 ≤ n ≤ M.
3. All leaf nodes in the B + tree contain all keywords and pointers to corresponding records, and all leaf nodes are linked in the order of keywords from small to large;
4. All non leaf nodes in the B + tree only play the role of index, that is, each index item in the node only contains the maximum keyword of the corresponding subtree and the pointer to the subtree, and does not contain the storage address of the record corresponding to the keyword.

4. Hash table lookup

①. Basic concepts of hash table

Hash table: it is a finite continuous address space and a storage structure.

Hash address: the storage location of the data element (record).

Generally, the hash table is a one-dimensional array, and the hash address is the subscript of the array.

Hash function: establish a definite correspondence h between the storage location p of the data element (record) and the keyword key, so that p=H(key). Call this correspondence h as the hash function and p as the hash address.

Hash method: select a function, calculate the storage location of elements according to the keyword according to the function, and store them according to this. When searching, the same function calculates the address of the given value k, and compares k with the element keyword in the address unit to determine whether the search is successful.

Conflict: different keywords are mapped to the same hash address, that is, key 1 ≠ key2, and H(key1)=H(key2). This phenomenon is called conflict, and key1 and key2 are synonymous with each other.

②. Construction method of hash function

direct addressing

That is, H(key)=a · key + b (a and b are constants).

• Advantages: this hash function is simple to calculate, and there can be no conflict.
• Disadvantages: when the distribution of keywords is basically continuous, the hash function of direct addressing method can be used; Otherwise, if the keyword distribution is discontinuous, it will cause a lot of waste of memory units.
• For example: H (student number) = student number - 201816010101
  

Division method

Set the length of the hash table as m, divide the keyword key by a number p not greater than m, and the remainder is used as the hash address.
The hash function H(key) of the division residue method is: H(key)=key mod p (mod is the remainder operation, P ≤ m)
The key of this method is to select the appropriate p. generally, p can be selected as the maximum prime number less than the table length. For example, if the table length is m = 100, p =97 can be taken.

③. Methods of dealing with conflicts

The actual meaning of "handling conflict" is to find the next hash address for the conflicting address.

Open address method

Basic method: when a conflict occurs, a detection sequence is formed; Probe other addresses in the hash table one by one according to this sequence until the given keyword or an empty address (open address) is found, and put the conflicting records into this address.

The calculation formula of the new hash address is:
Hi(key)=(H(key)+di)MOD m, i=1，2，...， k(k≤m-1)

Of which:

• H(key): hash function;
• m: Hash table length;
• di: incremental sequence at the i-th detection;
• Hi(key): the hash address obtained after the ith detection.

Detection: refers to the process of finding the "next" vacancy.

There are three methods for incremental di:

1. Linear detection method: detect the next address of d in turn, that is, in case of conflict, find the nearby (next) empty address to store. di = 1,2,3,… . … m-1
2. Secondary detection method: in case of conflict, find the empty position before and after di=12,-12,22,-23,32,... ± k2 (k ≤ m/2)
3. Random detection method: Di is a set of pseudo-random sequence or di = i × H2 (key) (also known as double hash function detection)

Chain address method

Basic idea: chain records with the same hash address into a single linked list, set M single linked lists for M hash addresses, and then use an array to store the header pointers of m single linked lists to form a dynamic structure

The synonyms stored in the single linked list are called synonym linked list. In this method, what is stored in each cell of the hash table is no longer the record itself, but the header pointer of the corresponding synonym single chain table

④. Hash table lookup

The hash table lookup process is consistent with the table creation process. Take the open addressing method as an example:

1. Find the hash address of k
2. If there is an empty record at this position in the table, the search fails and returns; You can also fill in the record with keyword equal to k
3. If the component is not empty and the keyword = k, it will be returned successfully; Otherwise, find the next address according to the set conflict handling method
4. Repeat the first two steps

#include<stdio.h>
#include<malloc.h>
#include<string.h>
#define MaxSize 1000
typedef struct node
{
    int key;
    struct node *next;
}NodeType;
typedef struct
{
    NodeType*first;
}HashTable;
HashTable ha[MaxSize];//Hashtable 
int keys[MaxSize];//Save key value
void Insert(HashTable ha[],int m,int key)
{
    int adr;
    adr=key%m;//Keyword% hash table length
    NodeType *q;
    q=(NodeType*)malloc(sizeof(NodeType));
    q->key=key;
    q->next=NULL;
    //Form a hash table of an address through a link
    if(ha[adr].first==NULL)
    {
        ha[adr].first=q;
    }else//Head insertion
    {
        q->next=ha[adr].first;
        ha[adr].first=q;
    }
}
void Seek(HashTable ha[],int m,int k)
{
    int i=0,adr;
    adr=k%m;
    //A hash table that determines which address it is
    NodeType *q;
    q=ha[adr].first;
    //q is the header pointer of the hash table of the current address
    while(q!=NULL)
    {
        i++;
        if(q->key==k) break;
        q=q->next;
    }
    if(q!=NULL)
    printf("%d,%d",adr,i);
    else
    printf("-1");
}
int main()
{
    int m,n,k;
    scanf("%d",&m);//Hash table length
    scanf("%d",&n);//Number of keywords
    for(int i=0;i<n;i++)
    {
        scanf("%d",&keys[i]);//Keyword set
    }
    for(int i=0;i<m;i++)
    {
        ha[i].first=NULL;
    }
    for(int i=0;i<n;i++)
    {
        Insert(ha,m,keys[i]);///Insert hash table
    }
    scanf("%d",&k);
    Seek(ha,m,k);
}

Example:

5. Summary

Lookup is an operation often used in data processing. This chapter mainly introduces the lookup table, which is actually just a set. In order to improve the lookup efficiency, the lookup table is organized into different data structures, mainly including three kinds of lookup tables with different structures: linear table, tree table and hash table.

(1) linear lookup table. It mainly includes sequential search, half search and block search.

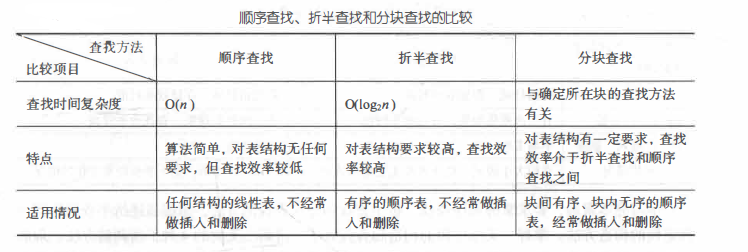
(2) Tree table lookup. The structure of tree table mainly includes binary sort tree, balanced binary tree, B-tree and B + tree.

① The search process of binary sort tree is similar to that of half search.

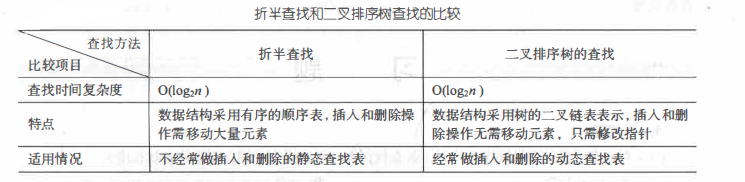
② The binary sort tree has the best performance when the shape is uniform, while its search performance when the shape is a single tree degenerates to the same as the sequential search. Therefore, the binary sort tree is better to be a balanced binary tree. The balance adjustment method of balanced binary tree is to ensure that the depth of binary sort tree is O(logzn) in any case. There are four balance adjustment methods: LL type, RR type, LR type and RL type.

③ B-tree is a balanced multi fork search tree, which is a dynamic index technology commonly used in external storage file system. The process of searching on B-tree is similar to that of binary sort tree. It is a cross process of searching nodes along the pointer and searching keywords in nodes. In order to ensure the definition of B-tree, inserting a keyword in B-tree may produce "splitting" of nodes, while deleting a keyword may produce "merging" of nodes.

④ B + tree is a variant of B-tree, which is more suitable for file system indexing. The process of random search, insertion and deletion on B + tree is basically similar to that of B-tree, but the specific implementation details are different.

(3) Hash table lookup. Hash table also belongs to linear structure, but it is essentially different from the search of linear table. It does not search based on keyword comparison, but establishes the corresponding relationship between the keyword of the record and its position in the table through a hash function, and adopts a special method to deal with the conflict when there is a conflict in the storage record. The hash table constructed in this way not only has no relationship between the average search length and the total number of records, but also can control the average search length within the required range by adjusting the loading factor.

Hash lookup method mainly studies two problems: how to construct hash function and how to deal with conflict.

① There are many methods to construct hash function, and the remainder method is the most commonly used method to construct hash function. It can not only take the module of keywords directly, but also take the module after folding and square operation.

② The methods to deal with conflicts are usually divided into two categories: open address method and chain address method. The difference between them is similar to the difference between sequential table and single chain table.

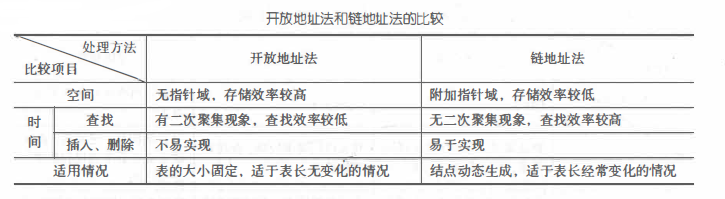
6. Examples and Applications

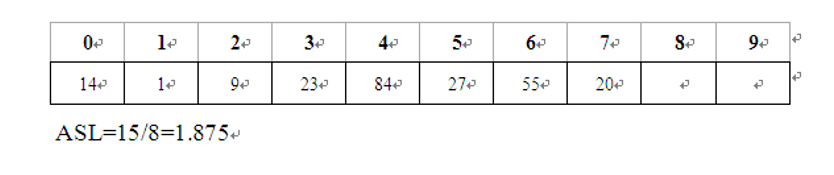
Use the division and remainder method to create the hash table, use any method to deal with the conflict to solve the conflict, and calculate the average search length of the hash table. Programming realizes the following functions:
Given a set of keywords (19,14,23,1,68,20,84,27,55,11,10,79), the hash function is defined as: H(key)=key MOD 13, and the hash table length is m=16. Hash the hash table and calculate the average search length (assuming that the search probability of each record is equal).
(1) The hash table is defined as a fixed length array structure;
(2) Using linear detection hashing or chain address method to solve the conflict;
(3) After the hash is completed, output the array content or linked list on the screen;
(4) Output the average search length under equal probability search;
(5) After completing the hash, enter the keyword to complete the search operation. Test the success and failure of the search respectively.

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define N 13
#define Hashsize 16

int sign = 2;

typedef struct Hash
{
	int date;
	int sign;
} HashNode;
//Linear conflict handling
void compare(HashNode H[], int p, int i, int key[])
{
	p++;
	if (H[p].sign != 0)
	{
		sign++;
		compare(H, p, i, key);
	}
	else
	{
		H[p].date = key[i];
		H[p].sign = sign;
		sign = 2;
	}
}

void Hashlist(HashNode H[], int key[])
{
	int p;
	for (int i = 0; i < 12; i++)
	{
		p = key[i] % N;

		if (H[p].sign == 0)
		{
			H[p].date = key[i];
			H[p].sign = 1;
		}
		else
			compare(H, p, i, key);
	}
}
//Find conflict handling
int judge(HashNode H[], int num, int n)
{
	n++;

	if (n >= Hashsize)
		return 0;

	if (H[n].date == num)
	{
		printf("position\t data\n");
		printf("%d\t %d\n\n", n, H[n].date);
		return 1;
	}
	else
	{
		judge(H, num, n);
	}
}
//lookup
int search(char num, HashNode H[])
{
	int n;
	n = num % N;
	if (H[n].sign == 0)
	{
		printf("Search failed!");
		return 0;
	}
	if (H[n].sign != 0 && H[n].date == num)
	{
		printf("position\t data\n");
		printf("%d\t %d\n", n, H[n].date);
	}
	else if (H[n].sign != 0 && H[n].date != num)
	{
		if (judge(H, num, n) == 0)
			return 0;
	}
	return 1;
}

int main(void)
{
	int key[N] = {19, 14, 23, 1, 68, 20, 84, 27, 55, 11, 10, 79};
	float a = 0;
	HashNode H[Hashsize];
	for (int i = 0; i < Hashsize; i++)
		H[i].sign = 0;
	Hashlist(H, key);
	printf("The established hash table is shown below:\n position\t\t data\n");
	for (int i = 0; i < Hashsize; i++)
	{
		if (H[i].sign != 0)
		{
			printf("%d\t-->\t%d\n", i, H[i].date);
		}
		else
		{
			H[i].date = 0;
			printf("%d\t-->\t%d\n", i, H[i].date);
		}
	}
	int num;
	printf("Enter search value(input-1 sign out):\n");
	for (int i = 0;; i++)
	{
		scanf("%d", &num);
		if (num == -1)
			break;
		if (search(num, H) == 0)
			printf("The value does not exist!\n");
	}
	for (int i = 0; i < Hashsize; i++)
	{
		a = a + H[i].sign;
	}
	printf("Average search length:%0.2f\n", a / 12);
	return 0;
}