1. Basic concepts of sorting

Sorting is an operation often carried out in the computer. Its purpose is to adjust a group of "unordered" record sequences to "ordered" record sequences. The purpose of sorting is to facilitate searching.

If the whole sorting process can be completed without accessing external memory, this kind of sorting problem is called internal sorting;
If there is a large number of external records in the sorting process, it is called the problem that the number of external records in the sorting process is not possible. On the contrary, it must participate in the sorting process.

Classification of internal sorting methods

• Insert sort (direct insert, half insert, Hill sort)
  One or more records in the unordered subsequence are "inserted" into the ordered sequence, thereby increasing the length of the ordered subsequence of records.

• Swap sort (bubble sort, quick sort)
  By "exchanging" the records in the unordered sequence, the record with the smallest or largest keyword is obtained, and it is added to the ordered subsequence to increase the length of the ordered subsequence.

• Selection sorting (simple selection, tree selection, heap sorting)
  Select the record with the smallest or largest keyword from the unordered subsequence of records and add it to the ordered subsequence to increase the length of the ordered subsequence of records.

• Merge sort
  By "merging" two or more ordered subsequences of records, the length of the ordered sequence of records is gradually increased.

• Cardinality sort
  There is no need to compare keywords. According to the idea of "multi keyword" sorting, the method of sorting single logical keywords with the help of "allocation" and "collection".

Storage methods of records to be sorted: sequence table, linked list and address vector

Evaluation index of sorting algorithm efficiency

1. Time efficiency - sorting speed (comparison times and movement times)
2. Space efficiency -- the amount of auxiliary memory space
3. Stability - if the keywords of A and B are equal and the order of A and B remains unchanged after sorting, this sorting algorithm is said to be stable.

2. Insert sort

The basic idea of inserting and sorting is: insert a record to be sorted into the appropriate position of a group of records that have been arranged according to the size of its keyword in each trip until all records to be sorted are inserted.

①. Direct insert sort

Straight insertion sort is the simplest sort method. Its basic operation is to insert records into the ordered table, so as to get a new ordered table with the number of records increased by 1.

Direct insertion sorting algorithm steps:

• Let the records to be sorted be stored in the array r[1... n], and r[1] is an ordered sequence.
• Cycle n -1 times, and use the sequential search method each time to find the insertion position of r[i](i=2,..., n) in the ordered sequence r[1... i-1], and then insert r[i] into the ordered sequence r[1... i-1] with table length i-1 until r[n] is inserted into the ordered sequence r[1... N-1] with table length n-1, and finally get an ordered sequence with table length n.

//Direct insert sort
#include <iostream>
using namespace std;
#define  MAXSIZE  20           						// Maximum length of sequence table
typedef struct
{
	int key;
	char *otherinfo;
}ElemType;
//Storage structure of sequential table                         
typedef struct
{
    ElemType *r;	         						//Base address of storage space
    int  length;            						//Sequence table length
}SqList;											//Sequence table type

void InsertSort(SqList &L)
{
   //Direct insertion sorting of sequence table L
	int i,j;
	for(i=2;i<=L.length;++i)
		if(L.r[i].key<L.r[i-1].key)
		{   										//"<", you need to insert r[i] into the ordered sub table
			L.r[0]=L.r[i];				 			//Temporarily store the records to be inserted in the monitoring post
            L.r[i]=L.r[i-1];	            		//r[i-1] backward
            for(j=i-2; L.r[0].key<L.r[j].key;--j)			//Find the insertion position from the back to the front
				L.r[j+1]=L.r[j];					//Move the records back one by one until the insertion position is found
            L.r[j+1]=L.r[0];						//Insert r[0], the original r[i], into the correct position
		}											//if
}													//InsertSort

void Create_Sq(SqList &L)
{
	int i,n;
	cout<<"Please enter the number of data, no more than"<<MAXSIZE<<"One."<<endl;
	cin>>n;											//Enter number
	cout<<"Please enter the data to be sorted:\n";
	while(n>MAXSIZE)
	{
		cout<<"The number exceeds the upper limit and cannot exceed"<<MAXSIZE<<"，Please re-enter"<<endl;
		cin>>n;
	}
	for(i=1;i<=n;i++)
	{
		cin>>L.r[i].key;
		L.length++;
	}
}
void show(SqList L)
{
	int i;
	for(i=1;i<=L.length;i++)
		cout<<L.r[i].key<<endl;
}

void main()
{
	SqList L;
	L.r=new ElemType[MAXSIZE+1];
	L.length=0;
	Create_Sq(L);
	InsertSort(L);
	cout<<"The sorted results are:"<<endl;
	show(L);
}

For example: it is known that the keyword sequence of the records to be sorted is {49,38,65,97,76,13,27,49}. The process of sorting by direct insertion sorting method.

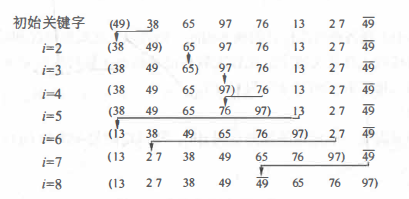
Direct insertion sorting features:

• Stable sorting.
• The algorithm is simple and easy to implement.
• It is also applicable to the linked storage structure, but there is no need to move records on the single linked list, just modify the corresponding pointer.
• It is more suitable for the case that the initial records are basically in order (positive order). When the initial records are out of order and n is large, the time complexity of this algorithm is high and should not be used.

②. Binary Insertion Sort

Half insertion sorting algorithm steps:

1. Let the records to be sorted be stored in the array r[1... n], and r[1] is an ordered sequence.
2. Cycle n-1 times, and use the half search method each time to find r i At the insertion position in the ordered sequence r[1... i-1], then insert r[i] into the ordered sequence r[1... i-1] with table length i-1 until r[n] is inserted into the ordered sequence r with table length n-l[
   1... n-1], and finally get an ordered sequence with table length n.

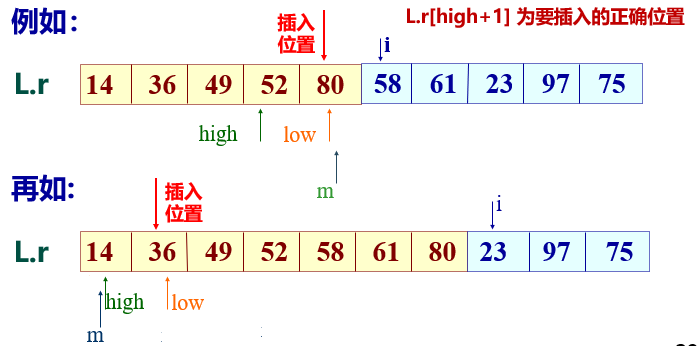
//Binary Insertion Sort 
#include <iostream>
using namespace std;
#define  MAXSIZE  20           			// Maximum length of sequence table
typedef struct
{
	int key;
	char *otherinfo;
}ElemType;
//Storage structure of sequential table                         
typedef struct
{
    ElemType *r;	         						//Base address of storage space
    int  length;            						//Sequence table length
}SqList;											//Sequence table

void BInsertSort(SqList &L){
	//Sort the order table L by half insertion
	int i,j,low,high,m;
	for(i=2;i<=L.length;++i)
	{
		L.r[0]=L.r[i];          					//Temporarily store the records to be inserted in the monitoring post
		low=1; high=i-1;        					//Set initial value of search interval
		while(low<=high)
		{											//Find the insertion position in half in r[low..high]
			m=(low+high)/2;             			//Halve
			if(L.r[0].key<L.r[m].key)  high=m-1;	//The insertion point is in the previous sub table
			else  low=m+1;					   		//The insertion point is in the next sub table
		}//while
		for(j=i-1;j>=high+1;--j)  L.r[j+1]=L.r[j];	//Record backward
		L.r[high+1]=L.r[0];							//Insert r[0], the original r[i], into the correct position
    }												//for
}													//BInsertSort

void Create_Sq(SqList &L)
{
	int i,n;
	cout<<"Please enter the number of data, no more than"<<MAXSIZE<<"One."<<endl;
	cin>>n;											//Enter number
	cout<<"Please enter the data to be sorted:\n";
	while(n>MAXSIZE)
	{
		cout<<"The number exceeds the upper limit and cannot exceed"<<MAXSIZE<<"，Please re-enter"<<endl;
		cin>>n;
	}
	for(i=1;i<=n;i++)
	{
		cin>>L.r[i].key;
		L.length++;
	}
}

void show(SqList L)
{
	int i;
	for(i=1;i<=L.length;i++)
		cout<<L.r[i].key<<endl;
}

void main()
{
	SqList L;
	L.r=new ElemType[MAXSIZE+1];
	L.length=0;
	Create_Sq(L);
	BInsertSort(L);
	cout<<"The sorted results are:"<<endl;
	show(L);
}

Half insertion sorting features:

• Stable sorting.
• Because it is necessary to perform half search, it can only be used for sequential structure, not chain structure.
• It is suitable for the situation when the initial record is out of order and n is large.

③. Shell Sort

Hill sort: first divide the whole record sequence to be arranged into several subsequences for direct insertion sort. When the records in the whole sequence are "basically orderly", then carry out a direct insertion sort for all records.

//Shell Sort 
#include <iostream>
using namespace std;
#define  MAXSIZE  20           			// Maximum length of sequence table
typedef struct
{
	int key;
	char *otherinfo;
}ElemType;
//Storage structure of sequential table                         
typedef struct
{
    ElemType *r;	         						//Base address of storage space
    int  length;            						//Sequence table length
}SqList;											//Sequence table type

void ShellInsert(SqList &L,int dk)
{
	//Do a hill insertion sort with an increment of dk for the sequence table L
	int i,j;
	for(i=dk+1;i<=L.length;++i)
		if(L.r[i].key<L.r[i-dk].key)
		{										//L.r[i] needs to be inserted into the ordered quantum table
			L.r[0]=L.r[i];						//Temporarily existing L.r[0]
			for(j=i-dk;j>0&& L.r[0].key<L.r[j].key;j-=dk)
				L.r[j+dk]=L.r[j];				//Move the record back until the insertion position is found
			L.r[j+dk]=L.r[0];					//Insert r[0], the original r[i], into the correct position
		}										//for
}
												//ShellInsert
void ShellSort(SqList &L,int dt[ ],int t){
   //Sort the order table L by the increment sequence dt[0..t-1]
	int k;
    for(k=0;k<t;++k)
        ShellInsert(L,dt[k]);			 		//A hill insertion sort with an increment of dt[t]
}												//ShellSort

void Create_Sq(SqList &L)
{
	int i,n;
	cout<<"Please enter the number of data, no more than"<<MAXSIZE<<"One."<<endl;
	cin>>n;										//Enter number
	cout<<"Please enter the data to be sorted:\n";
	while(n>MAXSIZE)
	{
		cout<<"The number exceeds the upper limit and cannot exceed"<<MAXSIZE<<"，Please re-enter"<<endl;
		cin>>n;
	}
	for(i=1;i<=n;i++)
	{
		cin>>L.r[i].key;
		L.length++;
	}
}

void show(SqList L)
{
	int i;
	for(i=1;i<=L.length;i++)
		cout<<L.r[i].key<<endl;
}

void main()
{
	SqList L;
	L.r=new ElemType[MAXSIZE+1];
	L.length=0;
	Create_Sq(L);
	
	int i,t;//Length of incremental array
	int *dt=new int[MAXSIZE];//Incremental array
	cout<<"Please enter the number of increments:\n";
	cin>>t;
	for(i=0;i<t;i++)
	{
		cout<<"The first"<<i+1<<"Increment:\n";
		cin>>dt[i];
	}
	ShellSort(L,dt,t);
	cout<<"The sorted results are:"<<endl;
	show(L);
}

Hill sorting features:

• The jumping movement of records causes the sorting method to be unstable.
• It can only be used for sequential structure, not chain structure.
• The incremental sequence can have various methods, but the value in the incremental sequence should have no common factor other than 1, and the last incremental value must be equal to 1.
• The total comparison times and movement times of records are less than those of direct insertion sequencing. The greater the n, the more obvious the effect is. Therefore, it is suitable for the case when the initial record is disordered and n is large.

3. Exchange sort

The basic idea of exchange sorting is: compare the keywords of the records to be sorted in pairs. Once it is found that the two records do not meet the order requirements, exchange them until the whole sequence meets the requirements.

①. Bubble sorting

Bubble sort is the simplest exchange sort method. It compares the keywords of adjacent records in pairs. If the reverse order occurs, it will be exchanged, so that the records with small keywords will gradually "float" (move left) upward like bubbles, or the records with large key words will gradually "fall" (move right) downward like stones.

Bubble sorting algorithm steps:

1. Set the records to be sorted to be stored in the array r[1... N]. First, compare the keywords of the first record with those of the second record. If it is in reverse order (i.e. L.r[1]. Key > L.R [2]. Key), exchange the two records. Then compare the keywords of the second record and the third record. And so on until the keywords of record n-1 and record n are compared. The above process is called the first bubble sort, and the result is that the record with the largest keyword is placed in the position of the last record.
2. Then conduct the second bubble sorting, and do the same for the first n-1 records. As a result, the record with the second largest keyword is placed at the position of the N-1 record.
3. Repeat the above comparison and exchange process. The ith pass is to compare the keywords of two adjacent records from L.r[1] to L.r[n-i+l], and exchange adjacent records in "reverse order". As a result, the record with the largest keyword in the n-i+1 records is exchanged to the position of n-i+1. Until there is no record exchange operation in a certain sorting process, indicating that all sequences have met the sorting requirements, the sorting is completed.

//Bubble sorting
#include <iostream>
using namespace std;
#define  MAXSIZE  20           			// Maximum length of sequence table
typedef struct
{
	int key;
	char *otherinfo;
}ElemType;
//Storage structure of sequential table                         
typedef struct
{
    ElemType *r;	         						//Base address of storage space
    int  length;            						//Sequence table length
}SqList;											//Sequence table type

void BubbleSort(SqList &L)
{
	//Bubble sort the order table L
	int m,j,flag;
	ElemType t;
    m=L.length-1; flag=1; 				//flag is used to mark whether a certain sort is exchanged
    while((m>0)&&(flag==1))
	{
		flag=0;           				//flag is set to 0. If there is no exchange in this sorting, the next sorting will not be executed
        for(j=1;j<=m;j++)
			if(L.r[j].key>L.r[j+1].key) 
			{
				flag=1;					//flag is set to 1, indicating that the sorting has been exchanged
				t=L.r[j];L.r[j]=L.r[j+1];L.r[j+1]=t;	//Two records before and after exchange
			}							//if
		--m;
    }									//while
}										//BubbleSort

void Create_Sq(SqList &L)
{
	int i,n;
	cout<<"Please enter the number of data, no more than"<<MAXSIZE<<"One."<<endl;
	cin>>n;											//Enter number
	cout<<"Please enter the data to be sorted:\n";
	while(n>MAXSIZE)
	{
		cout<<"The number exceeds the upper limit and cannot exceed"<<MAXSIZE<<"，Please re-enter"<<endl;
		cin>>n;
	}
	for(i=1;i<=n;i++)
	{
		cin>>L.r[i].key;
		L.length++;
	}
}

void show(SqList L)
{
	int i;
	for(i=1;i<=L.length;i++)
		cout<<L.r[i].key<<endl;
}

void main()
{
	SqList L;
	L.r=new ElemType[MAXSIZE+1];
	L.length=0;
	Create_Sq(L);
	BubbleSort(L);
	cout<<"The sorted results are:"<<endl;
	show(L);
}

Example:

Bubble sorting features:

1. Stable sorting.
2. It can be used for chain storage structure.
3. There are many times of moving records, and the average time performance of the algorithm is worse than that of direct insertion sorting. When the initial records are out of order and n is large, this algorithm is not suitable.

②. Quick sort

Quick Sort is improved from bubble sort. In the process of bubble sort, only two adjacent records are compared, so only one reverse order can be eliminated when exchanging two adjacent records each time. If multiple reverse orders can be eliminated through one exchange of two (non adjacent) records, the sorting speed will be greatly accelerated. One exchange in a Quick Sort method may eliminate multiple reverse orders.

Quick sort algorithm steps:

1. Select the first record in the table to be sorted as the pivot and temporarily store the pivot record in the position of r[0] Two pointers low and high are attached. Initially, they point to the lower and upper bounds of the table respectively (in the first trip, low= 1; high= L.length;)
2. Search to the left from the rightmost position of the table, find the record with the first keyword less than the pivot keyword pivotkey, and move it to low. The specific operations are as follows: when low < high, if the keyword of the record indicated by high is greater than or equal to pivotkey, move the pointer high to the left (execute operation – high); Otherwise, move the record indicated by high to the record indicated by low.
3. Then, from the leftmost position of the table, search to the right in turn to find the record with the first keyword greater than pivotkey and pivot record exchange. The specific operations are as follows: when low < high, if the keyword of the record referred to by low is less than or equal to pivotkey, move the pointer low to the right (execute operation + + low); Otherwise, the record referred to by low will be exchanged with the pivot record.
4. Repeat steps ② and ③ until low and high are equal. At this time, the position of low or high is the final position of the pivot in this sort. The original table is divided into two sub tables.

In the above process, the records are exchanged with the pivot, and the records must be moved three times each time. The pivot records can be temporarily stored in the position of r[0], and only the records to be exchanged with the pivot can be moved in the sorting process, that is, only the one-way movement of r[low] or r[high], and then the pivot records can be moved to the correct position until the end of one sorting.

//Quick sort
#include <iostream>
using namespace std;
#define  MAXSIZE  20           			// Maximum length of sequence table
typedef struct
{
	int key;
	char *otherinfo;
}ElemType;
//Storage structure of sequential table                         
typedef struct
{
    ElemType *r;	         						//Base address of storage space
    int  length;            						//Sequence table length
}SqList;											//Sequence table type


int Partition(SqList &L,int low,int high)
{ 
	//Sort the sub table r[low..high] in the order table L once and return to the pivot position
	int pivotkey;
	L.r[0]=L.r[low];                    	//Use the first record of the sub table as the pivot record
	pivotkey=L.r[low].key;		   			//Pivot record keywords are saved in pivotkey
	while(low<high)
	{										//Scan alternately from both ends of the table to the middle
		while(low<high&&L.r[high].key>=pivotkey) --high;
		L.r[low]=L.r[high];					//Move records smaller than pivot records to the low end
		while(low<high&&L.r[low].key<=pivotkey) ++low;
		L.r[high]=L.r[low];					//Move records larger than pivot records to the high end
	}//while
	L.r[low]=L.r[0];						//Pivot record in place
	return  low;							//Return to pivot position
}//Partition

void QSort(SqList &L,int low,int high)
{	//Call the pre initial value: low=1; high=L.length;
    //Quickly sort the subsequence L.r[low..high] in the order table L
	int pivotloc;
    if(low<high)
	{										//Length greater than 1
       pivotloc=Partition(L,low,high); 		//Divide L.r[low..high] into two, and pivot LOC is the pivot position
       QSort(L,low,pivotloc-1);				//Recursively sort the left sub table
       QSort(L,pivotloc+1,high);        	//Recursive sorting of right sub table
	}
}											//QSort

void QuickSort(SqList &L)
{
   //Quick sort the order table L
   QSort(L,1,L.length);
}											//QuickSort
								
void Create_Sq(SqList &L)
{
	int i,n;
	cout<<"Please enter the number of data, no more than"<<MAXSIZE<<"One."<<endl;
	cin>>n;											//Enter number
	cout<<"Please enter the data to be sorted:\n";
	while(n>MAXSIZE)
	{
		cout<<"The number exceeds the upper limit and cannot exceed"<<MAXSIZE<<"，Please re-enter"<<endl;
		cin>>n;
	}
	for(i=1;i<=n;i++)
	{
		cin>>L.r[i].key;
		L.length++;
	}
}


void show(SqList L)
{
	int i;
	for(i=1;i<=L.length;i++)
		cout<<L.r[i].key<<endl;
}


int main(void)
{
	SqList L;
	L.r=new ElemType[MAXSIZE+1];
	L.length=0;
	Create_Sq(L);
	QuickSort(L);
	cout<<"The sorted results are:"<<endl;
	show(L);
}

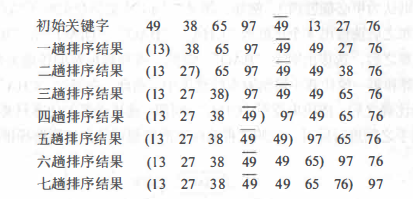
Example: it is known that the keyword sequence of the records to be sorted is {49,38,65,97,76,13,27,49}, and the sorting process is carried out by quick sorting method.

Example:

Quick sort features:

1. The non sequential movement of records leads to the instability of the sorting method.
2. It is necessary to locate the lower and upper bounds of the table in the sorting process, so it is suitable for sequential structure and difficult for chain structure.
3. When n is large, on average, quick sort is the fastest of all internal sorting methods, so it is suitable for the case of disordered initial records and large n.

4. Select sort

The basic idea of selective sorting is to select the record with the smallest keyword from the records to be sorted in each trip and put it at the end of the sorted record sequence until all the records are arranged.

①. Simple selection sort

Simple selection sort is also called direct selection sort

Simple selection sorting algorithm steps:

1. Set the records to be sorted to be stored in the array r[l... N]. The first trip starts from r[1], and through n-1 comparisons, select the record with the smallest keyword from n records, record it as r[k], and exchange r[1] and r[k].
2. The second trip starts from r[2], through n-2 comparisons, select the record with the smallest keyword from n-l records, record it as r[k], and exchange r[2] and r[k].
3. By analogy, the i-th trip starts from r[i]. Through n-i comparison, select the record with the smallest keyword from n-i+tl records, record it as r[k], and exchange r[i] and r[k].
4. After n-1 times, the sorting is completed.

//Simple selection sort
#include <iostream>
using namespace std;
#define  MAXSIZE  20           						// Maximum length of sequence table
typedef struct
{
	int key;
	char *otherinfo;
}ElemType;
//Storage structure of sequential table                         
typedef struct
{
    ElemType *r;	         						//Base address of storage space
    int  length;            						//Sequence table length
}SqList;											//Sequence table type

void SelectSort(SqList &L) 
{ 
   //Make a simple selection and sort on the order table L
	int i,j,k;
	ElemType t;
    for(i=1;i<L.length;++i) 
	{  												//Select the record with the smallest keyword in L.r[i..L.length]
		k=i;                 
        for(j=i+1;j<=L.length;++j)
			if(L.r[j].key<L.r[k].key)  k=j;			//k refers to the record with the smallest keyword in this sort
		if(k!=i) {t=L.r[i];L.r[i]=L.r[k];L.r[k]=t;} //Exchange r[i] and r[k]        
     }												//for  
}													// SelectSort
								
void Create_Sq(SqList &L)
{
	int i,n;
	cout<<"Please enter the number of data, no more than"<<MAXSIZE<<"One."<<endl;
	cin>>n;											//Enter number
	cout<<"Please enter the data to be sorted:\n";
	while(n>MAXSIZE)
	{
		cout<<"The number exceeds the upper limit and cannot exceed"<<MAXSIZE<<"，Please re-enter"<<endl;
		cin>>n;
	}
	for(i=1;i<=n;i++)
	{
		cin>>L.r[i].key;
		L.length++;
	}
}

void show(SqList L)
{
	int i;
	for(i=1;i<=L.length;i++)
		cout<<L.r[i].key<<endl;
}

void main()
{
	SqList L;
	L.r=new ElemType[MAXSIZE+1];
	L.length=0;
	Create_Sq(L);
	SelectSort(L);
	cout<<"The sorted results are:"<<endl;
	show(L);
}

For example, it is known that the keyword sequence of the records to be sorted is {49,38,65,97,49,13,27,76}, and the process of sorting by simple selection sorting method is given.

Simple selection sorting features:

1. As far as the selective sorting method itself is concerned, it is a stable sorting method, but the phenomenon shown in the example is unstable. This is because the above algorithm for selective sorting adopts the strategy of "exchanging records". By changing this strategy, we can write a selective sorting algorithm that does not produce "unstable phenomenon".
2. It can be used for chain storage structure.
3. The number of moving records is less. When each record occupies more space, this method is faster than direct insertion sorting.

②. Tree Selection Sort

Tree selection sort: also known as tournament sort, it is a method of selecting and sorting according to the idea of tournament. With the help of a complete binary tree with n leaf nodes, pairwise comparison selects the smallest. This process can be represented by a complete binary tree with n leaf nodes.

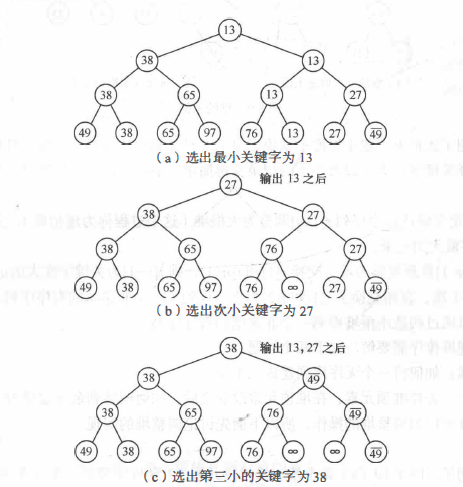
③. Heap sort

Heap Sort is a tree selection sort. In the sorting process, the records to be sorted r[1... n] are regarded as the sequential storage structure of a complete binary tree. Using the internal relationship between parent nodes and child nodes in the complete binary tree, the records with the largest (or smallest) keyword are selected in the current unordered sequence.

Definition of heap:

The sequence {k1,k2,..., kn} of n elements is called heap if and only if the following conditions are met:

1. Ki ≥ k2i and ki ≥ k2i + 1 (large top pile)
2. Or ki ≤ k2i and ki ≤ k2i + 1 (small top pile)

If the one-dimensional array corresponding to this sequence (i.e. using one-dimensional array as the storage structure of this sequence) is regarded as a complete binary tree, the heap is essentially a complete binary tree satisfying the following properties: the values of all non terminal nodes in the tree are not greater than (or less than) the values of their left and right child nodes.

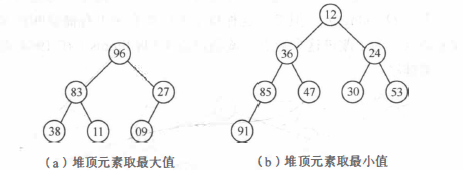
1. Adjust the sequence to be sorted r[1... N] to a large root heap according to the definition of heap (this process is called initial heap). Exchange r[1] and r[n], then r[n] is the record with the largest keyword.
2. Readjust r[1... N-1] to heap and exchange r[1] and r[n-1], then r[n-1] is the record with the second largest keyword.
3. Cycle n-1 times until r[1] and r[2] are exchanged, and a non decreasing ordered sequence r[1... N] is obtained.

Adjustment reactor

Let's take a look at an example. Figure (a) is a heap. After exchanging the top element 97 with the last element 38 in the heap, as shown in figure (b). At this time, all nodes except the root node meet the nature of the heap, so it is only necessary to adjust the nodes on one path from top to bottom. Firstly, the values of the heap top element 38 and its left and right subtree root nodes are compared. Since the value of the left subtree root node is greater than the value of the right subtree root node and greater than the value of the root node, 38 and 76 are exchanged; Since 38 replaces 76 and destroys the "heap" of the left subtree, it needs to make the same adjustment as above until the leaf node. The adjusted state is shown in figure (c). Repeat the above process, exchange and adjust the top element 76 and the last element 27 in the heap to obtain a new heap as shown in figure (d).

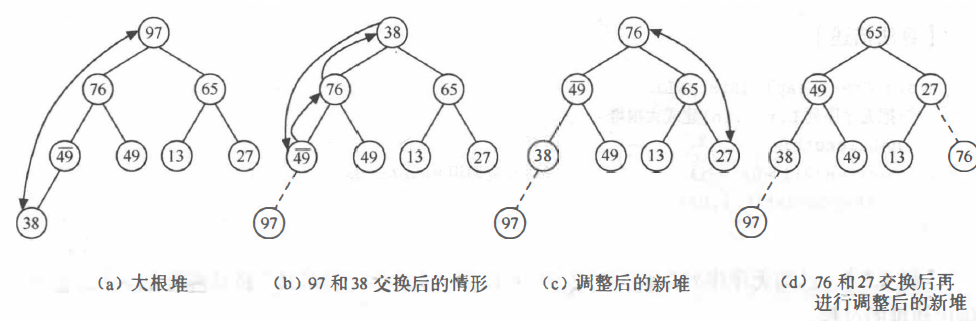
The above process is like sieving, screening the smaller keywords layer by layer, and selecting the larger keywords layer by layer. Therefore, this method is called "screening method".

Filter method adjustment heap:
Select the larger keyword from r[2s] and r[2s+I]. Assuming that the keyword of r[2s] is larger, compare the keywords of r[s] and r[2s].

1. If r[s] key> =r[2s]. Key, indicating that the subtree with r[s] as the root is already a heap and no adjustment is necessary.
2. If r[s] key<r[2s]. Key, exchange r[s] and R [2S]. After the exchange, the subtree with r[2s+I] as the root is still a heap. If the subtree with R [2S] as the root is not a heap, repeat the above process and adjust the subtree with R [2S] as the root to a heap until it reaches the leaf node.

//Screening adjustment reactor
#include <iostream>
using namespace std;
#define  MAXSIZE  20           						// Maximum length of sequence table
typedef struct
{
	int key;
	char *otherinfo;
}ElemType;
//Storage structure of sequential table                         
typedef struct
{
    ElemType *r;	         						//Base address of storage space
    int  length;            						//Sequence table length
}SqList;											//Sequence table type

void HeapAdjust(SqList &L,int s,int m)
{ 
   //Assuming that r[s+1..m] is already a heap, adjust r[s..m] to a large root heap with r[s] as the root
	ElemType rc;
	int j;
	rc=L.r[s];
    for(j=2*s;j<=m;j*=2)
	{												//Filter down the child nodes with larger key s
		if(j<m&&L.r[j].key<L.r[j+1].key) ++j;		//j is the subscript of the record with larger key
        if(rc.key>=L.r[j].key) break;      			//rc should be inserted in position s
		L.r[s]=L.r[j]; s=j; 
    }
	L.r[s]=rc;                          			//insert
}													//HeapAdjust
								
void Create_Sq(SqList &L)
{
	int i,n;
	cout<<"Please enter the number of data, no more than"<<MAXSIZE<<"One."<<endl;
	cin>>n;											//Enter number
	cout<<"Please enter the data to be adjusted:\n";
	while(n>MAXSIZE)
	{
		cout<<"The number exceeds the upper limit and cannot exceed"<<MAXSIZE<<"，Please re-enter"<<endl;
		cin>>n;
	}
	for(i=1;i<=n;i++)
	{
		cin>>L.r[i].key;
		L.length++;
	}
}
void show(SqList L)
{
	int i;
	for(i=1;i<=L.length;i++)
		cout<<L.r[i].key<<endl;
}
void main()
{
	SqList L;
	L.r=new ElemType[MAXSIZE+1];
	L.length=0;
	Create_Sq(L);
	HeapAdjust(L,1,L.length);
	cout<<"The adjusted result is:"<<endl;
	show(L);
}

Initial reactor

To adjust an unordered sequence to heap, we must adjust the subtree with each node as the root in its corresponding complete binary tree to heap. Obviously, a tree with only one node must be a heap, while in a complete binary tree, all nodes with sequence number greater than [n/2] are leaves, so the subtrees with these nodes as roots are already heaps. In this way, you only need to use the screening method to adjust the subtree of nodes with sequence numbers of | n/2], [n/2]-1..., 1 as the root to heap from the last branch node | n/2].
For the unordered sequence r[1... N], starting from i=n/2, repeatedly call the screening method HeapAdjust (L,in), and successively adjust the subtree with r cluster], r[i-1],..., r[1] as the root to the heap.

//Initial reactor
#include <iostream>
using namespace std;
#define  MAXSIZE  20           						// Maximum length of sequence table
typedef struct
{
	int key;
	char *otherinfo;
}ElemType;
//Storage structure of sequential table                         
typedef struct
{
    ElemType *r;	         						//Base address of storage space
    int  length;            						//Sequence table length
}SqList;											//Sequence table type

//Adjusting heap with algorithm 8.7 screening method
void HeapAdjust(SqList &L,int s,int m)
{ 
   //Assuming that r[s+1..m] is already a heap, adjust r[s..m] to a large root heap with r[s] as the root
	ElemType rc;
	int j;
	rc=L.r[s];
    for(j=2*s;j<=m;j*=2)
	{												//Filter down the child nodes with larger key s
		if(j<m&&L.r[j].key<L.r[j+1].key) ++j;		//j is the subscript of the record with larger key
        if(rc.key>=L.r[j].key) break;      			//rc should be inserted in position s
		L.r[s]=L.r[j]; s=j; 
    }
	L.r[s]=rc;                          			//insert
}													//HeapAdjust
								
void Create_Sq(SqList &L)
{
	int i,n;
	cout<<"Please enter the number of data, no more than"<<MAXSIZE<<"One."<<endl;
	cin>>n;											//Enter number
	cout<<"Please enter data:\n";
	while(n>MAXSIZE)
	{
		cout<<"The number exceeds the upper limit and cannot exceed"<<MAXSIZE<<"，Please re-enter"<<endl;
		cin>>n;
	}
	for(i=1;i<=n;i++)
	{
		cin>>L.r[i].key;
		L.length++;
	}
}

void CreatHeap(SqList &L)
{
	//Build the disordered sequence L.r[1..n] into a large root heap
	int i,n;
	n=L.length;
	for(i=n/2;i>0;--i)       					//Call HeapAdjust repeatedly 
		HeapAdjust(L,i,n);
}												//CreatHeap
void show(SqList L)
{
	int i;
	for(i=1;i<=L.length;i++)
		cout<<L.r[i].key<<endl;
}

void main()
{
	SqList L;
	L.r=new ElemType[MAXSIZE+1];
	L.length=0;
	Create_Sq(L);
	CreatHeap(L);
	cout<<"The sequence to build a heap is:"<<endl;
	show(L);
}

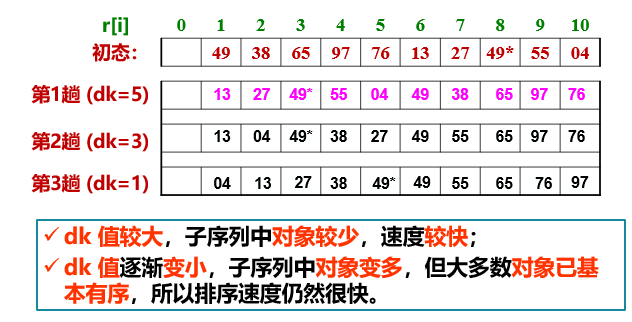
Example:

The known disordered sequence is {49,38,65,97,76,13,27,49}, which is adjusted to a large root heap by "screening method", and the process of heap building is given.

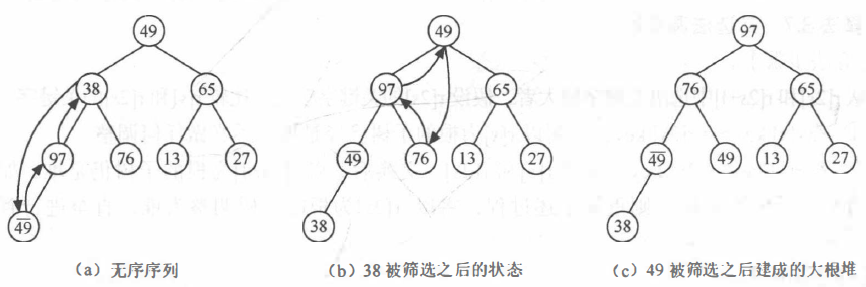
Implementation of heap sorting algorithm:

//sort
#include <iostream>
using namespace std;
#define  MAXSIZE  20           						// Maximum length of sequence table
typedef struct
{
	int key;
	char *otherinfo;
}ElemType;
//Storage structure of sequential table                         
typedef struct
{
    ElemType *r;	         						//Base address of storage space
    int  length;            						//Sequence table length
}SqList;											//Sequence table type

//Adjusting heap with algorithm 8.7 screening method
void HeapAdjust(SqList &L,int s,int m)
{ 
   //Assuming that r[s+1..m] is already a heap, adjust r[s..m] to a large root heap with r[s] as the root
	ElemType rc;
	int j;
	rc=L.r[s];
    for(j=2*s;j<=m;j*=2)
	{												//Filter down the child nodes with larger key s
		if(j<m&&L.r[j].key<L.r[j+1].key) ++j;		//j is the subscript of the record with larger key
        if(rc.key>=L.r[j].key) break;      			//rc should be inserted in position s
		L.r[s]=L.r[j]; s=j; 
    }
	L.r[s]=rc;                          			//insert
}
													//HeapAdjust								
void Create_Sq(SqList &L)
{
	int i,n;
	cout<<"Please enter the number of data, no more than"<<MAXSIZE<<"One."<<endl;
	cin>>n;											//Enter number
	cout<<"Please enter the data to be sorted:\n";
	while(n>MAXSIZE)
	{
		cout<<"The number exceeds the upper limit and cannot exceed"<<MAXSIZE<<"，Please re-enter"<<endl;
		cin>>n;
	}
	for(i=1;i<=n;i++)
	{
		cin>>L.r[i].key;
		L.length++;
	}
}

//Building initial reactor with algorithm 8.8
void CreatHeap(SqList &L)
{
	//Build the disordered sequence L.r[1..n] into a large root heap
	int i,n;
	n=L.length;
	for(i=n/2;i>0;--i)       					//Call HeapAdjust repeatedly 
		HeapAdjust(L,i,n);
}												//CreatHeap

void HeapSort(SqList &L) 
{ 
	//Heap sort order table L 
	int i;
	ElemType x;
	CreatHeap(L);              					//Build the unordered sequence L.r[1..L.length] into a large root heap 
	for(i=L.length;i>1;--i)
	{ 
		x=L.r[1];               				//Swap the top record with the last record in the current unordered subsequence L.r[1..i] 
		L.r[1]=L.r[i];            
		L.r[i]=x; 
		HeapAdjust(L,1,i-1);					//Readjust L.r[1..i-1] to large root heap 
   }//for 
}//HeapSort
void show(SqList L)
{
	int i;
	for(i=1;i<=L.length;i++)
		cout<<L.r[i].key<<endl;
}
void main()
{
	SqList L;
	L.r=new ElemType[MAXSIZE+1];
	L.length=0;
	Create_Sq(L);
	HeapSort(L);
	cout<<"The sorted results are:"<<endl;
	show(L);
}

Example: sort the built large root heap

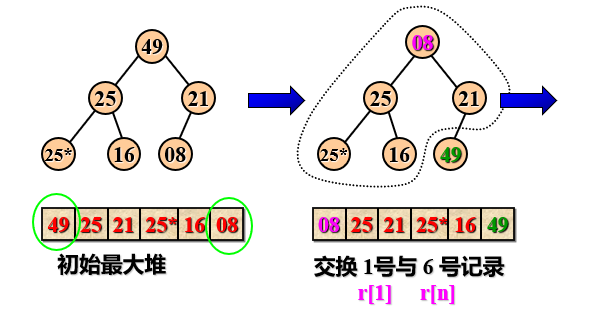
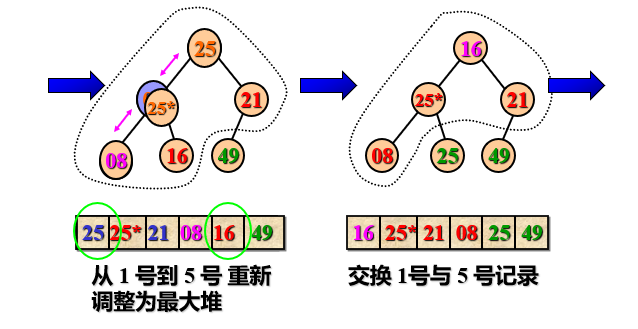
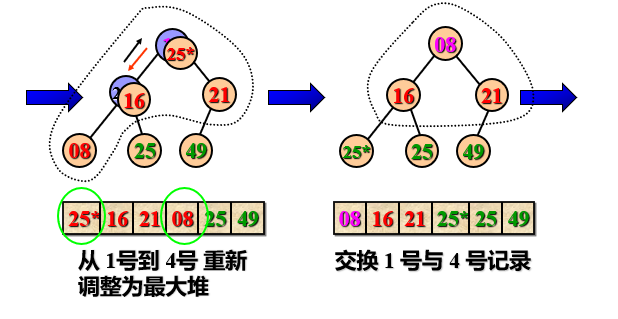
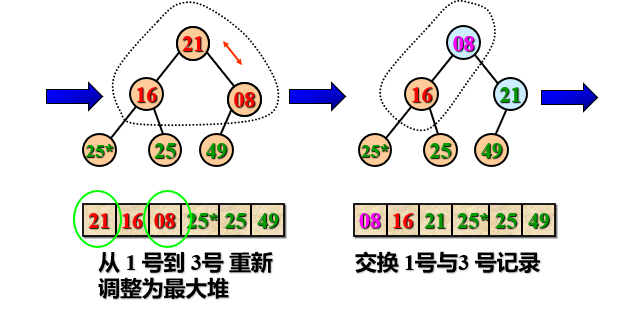
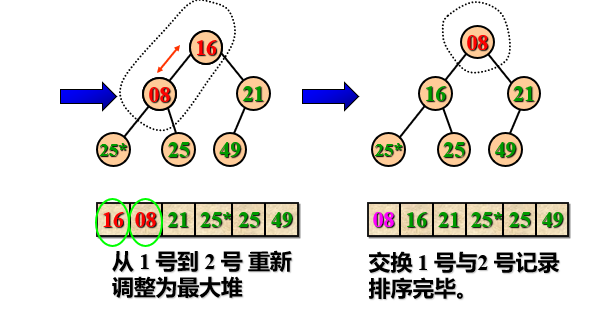
Heap sorting features:

1. Is an unstable sort.
2. It can only be used for sequential structure, not chain structure.
3. The number of comparisons required for initial reactor building is large, so it is not suitable to use when the number of records is small. The time complexity of heap sorting in the worst case is O(nlog2n), which is an advantage over O(n2) in the worst case of quick sorting. It is more efficient when there are many records.

5. Merge sort

Merging sort is the process of merging two or more ordered tables into one ordered table. The process of merging two ordered tables into one is called 2-way merging. 2-way merging is the simplest and most commonly used. Next, take 2-way merging as an example to introduce the merging sorting algorithm.

The idea of merging sorting algorithm is:

Assuming that the initial sequence contains n records, it can be regarded as n ordered subsequences. The length of each subsequence is 1, and then they are merged to obtain ⌈ n/2 ⌉ ordered subsequences with length of 2 or 1; Then merge two by two,... Repeat this until you get an ordered sequence with length n.

Merge sorting algorithm steps:

2-way merging and sorting merge and sort the records in R[low... high] and put them into T[low.high]. When the sequence length is equal to 1, the recursion ends, otherwise:

1. Divide the current sequence into two and find the split point mid = ⌊ (low+high)/2 ⌋;
2. The subsequence R[low... mid] is recursively merged and sorted, and the result is put into S[low... mid];
3. Recurse the subsequence R[mid + 1... high], merge and sort, and put the result into S[mid + 1... high];
4. Call the algorithm Merge to Merge the ordered two subsequences S[low... Mid] and S[mid +1... high] into an ordered sequence T[low... high].

//Merge sort
#include <iostream>
using namespace std;
#define  MAXSIZE  20           						// Maximum length of sequence table
typedef struct
{
	int key;
	char *otherinfo;
}RedType;

typedef struct
{
	RedType *r;
	int length;
}SqList;
																		
void Create_Sq(SqList &L)
{
	int i,n;
	cout<<"Please enter the number of data, no more than"<<MAXSIZE<<"One."<<endl;
	cin>>n;											//Enter number
	cout<<"Please enter the data to be sorted:\n";
	while(n>MAXSIZE)
	{
		cout<<"The number exceeds the upper limit and cannot exceed"<<MAXSIZE<<"，Please re-enter"<<endl;
		cin>>n;
	}
	for(i=1;i<=n;i++)
	{
		cin>>L.r[i].key;
		L.length++;
	}
}

//Merging of two adjacent ordered subsequences
void Merge(RedType R[],RedType T[],int low,int mid,int high)
{ 
   //Merge ordered tables R[low..mid] and R[mid+1..high] into ordered table T[low..high] 
	int i,j,k;
	i=low; j=mid+1;k=low; 
    while(i<=mid&&j<=high)
	{                 	
		//Merge the records in R from small to large into T 
		if(R[i].key<=R[j].key) T[k++]=R[i++]; 
        else T[k++]=R[j++]; 
	} 
	while(i<=mid)                            		//Copy the remaining R[low..mid] into T 
		T[k++]=R[i++];                 
	while(j<=high)                           		//Copy the remaining R[j.high] into T 
		T[k++]=R[j++];                       
}//Merge 

void MSort(RedType R[],RedType T[],int low,int high)
{ 
	//R[low..high] merge and sort and put it into T[low..high] 
	int mid;
	RedType *S=new RedType[MAXSIZE];
    if(low==high) T[low]=R[low]; 
    else
	{ 
		mid=(low+high)/2;       					//Divide the current sequence into two and find the split point mid 
        MSort(R,S,low,mid);							//The subsequence R[low..mid] is recursively merged and sorted, and the result is placed in S[low..mid] 
        MSort(R,S,mid+1,high);						//The subsequence R[mid+1..high] is recursively merged and sorted, and the result is placed in S[mid+1..high] 
        Merge(S,T,low,mid,high);					//Merge S[low..mid] and S [mid+1..high] into T[low..high]  
    }//else 
}// MSort 
 
void MergeSort(SqList &L)
{ 
	//Merge and sort the order table L 
    MSort(L.r,L.r,1,L.length); 
}//MergeSort 
void show(SqList L)
{
	int i;
	for(i=1;i<=L.length;i++)
		cout<<L.r[i].key<<endl;
}
void main()
{
	SqList R;
	R.r=new RedType[MAXSIZE+1];
	R.length=0;
	Create_Sq(R);
	MergeSort(R);
	cout<<"The sorted results are:"<<endl;
	show(R);
}

For example, it is known that the keyword sequence of the records to be sorted is {49,38,65,97,76,13,27}, and the sorting process by 2-way merging sorting method is given.

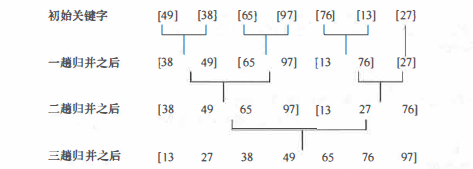
Merging and sorting features:

1. It is a stable sort.
2. It can be used for chain structure without additional storage space, but the corresponding recursive work stack still needs to be opened up in recursive implementation.

6. Cardinality sort

With the help of the idea of multi keyword sorting, single logical keywords are sorted. That is: sort with different bit values of keywords.

Multi keyword sorting

Example: how to sort a deck of playing cards?
If the order relationship between design and color and face value is specified as follows:
Decor:
Face value: 2 < 3 < 4 < 5 < 6 < 7 < 8 < 9 < 10 < J < Q < K < A
You can sort by design and color first, and then sort by face value if the design and color are the same; You can also sort by face value first, and then sort by design and color if the face value is the same.

There are usually two ways to implement multi keyword sorting:

Highest significant digital first (MSD)
Least significant digital first (LSD)

//Cardinality sort
#include <iostream.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#define MAXNUM_KEY 8                 	// Maximum number of keyword items 
#define RADIX 10 / / keyword cardinality. In this case, it is the cardinality of decimal integers 
#define MAX_SPACE 10000 
typedef char KeysType;					//Define the keyword type as character type
typedef int InfoType;					//Define the types of other data items
typedef struct
{ 
	KeysType keys[MAXNUM_KEY];          //keyword 
	InfoType otheritems;               	//Other data items 
	int next; 
}SLCell;						    	//Node type of static linked list 
typedef struct
{ 
	SLCell r[MAX_SPACE];		        //The available space of static linked list, r[0] is the head node 
	int keynum;				         	//Number of current keywords recorded 
	int recnum;					     	//Current length of static linked list 
}SLList;							    //Static linked list type 
typedef int ArrType[RADIX];	          	//Pointer array type

void InitList(SLList *L)
{ 
	//Initialize the static linked list L (store the data in Array D in L)
	char c[MAXNUM_KEY],c1[MAXNUM_KEY];
    int i,j,n,max;						//max is the maximum value of the keyword 
    max=-10000;
    cout<<"Please enter the number of data, no more than"<<MAX_SPACE<<"One.\n";
    cin>>n;
    while(n>MAX_SPACE)
    {
		cout<<"The number you entered exceeds the upper limit, please re-enter it, no more than"<<MAX_SPACE<<"One.\n";
	    cin>>n;
    }
    int *D=new int[n];
	cout<<"Please enter"<<n<<"Data sorted in rows:\n";
    for(i=0;i<n;i++)
    {
	    cin>>D[i];
	    if(max<D[i])
			max=D[i];
    }
    (*L).keynum=(int)(ceil(log10(max)));
    (*L).recnum=n;
    for(i=1;i<=n;i++)
    {
        itoa(D[i-1],c,10);					//Convert decimal integer into character type and store it in c 
		for(j=strlen(c);j<(*L).keynum;j++)  //If the length of c is less than the number of digits of Max, fill '0' before c 
		{
		   strcpy(c1,"0");
		   strcat(c1,c);
		   strcpy(c,c1);
		}
		for(j=0;j<(*L).keynum;j++)
			(*L).r[i].keys[j]=c[(*L).keynum-1-j];
    }
}

int ord(char c)
{	
	//Return the mapping of k (bit integer)
	return c-'0';
}
void Distribute(SLCell *r,int i,ArrType &f,ArrType &e)
{ 
	//The records in the r field of the static linked list L have been ordered according to (keys[0],..., keys[i-1]) 
	//This algorithm establishes a RADIX sub table according to the ith keyword keys[i], so that the keys[i] recorded in the same sub table are the same. 
	//f[0..RADIX-1] and e[0..RADIX-1] point to the first and last record in each sub table respectively
	int j,p;
	for(j=0;j<RADIX;++j)  f[j]=0;        	//Each sub table is initialized as an empty table 
	for(p=r[0].next;p;p=r[p].next)
	{ 
		j=ord(r[p].keys[i]);                //ord maps the ith keyword in the record to [0..RADIX-1] 
		if(!f[j])  f[j]=p; 
		else  r[e[j]].next=p; 
		e[j]=p;                          	//Insert the node indicated by p into the j th sub table 
	}//for 
}//Distribute 

int succ(int i)
{ 
	//Find successor function
    return ++i;
}
void Collect (SLCell *r,int i,ArrType &f,ArrType &e)
{ 
	//This algorithm links the sub tables referred to by f[0..RADIX-1] into a linked list from small to large according to the keys[i] 
    //e[0..RADIX-1] is the tail pointer of each sub table
	int j,t;
    for(j=0;!f[j];j=succ(j));  			//Find the first non empty sub table, and succ is the successor function 
    r[0].next=f[j];t=e[j];   			//r[0].next points to the first node in the first non empty sub table 
    while(j<RADIX-1)
	{ 
		for(j=succ(j);j<RADIX-1&&!f[j];j=succ(j)) ;       	//Find the next non empty sub table 
		if(f[j])  {r[t].next=f[j];t=e[j];}		        	//Link two non empty child tables 
	}//while 
	r[t].next=0;                		//t points to the last node in the last non empty sub table 
}//Collect 

void RadixSort(SLList &L)
{ 
	//L is a sequence table represented by a static linked list 
    //Sort L by cardinality, so that l becomes an ordered static linked list from small to large according to keywords, and L.r[0] is the head node
	int i;
	ArrType f,e;
    for(i=0;i<L.recnum;++i)  L.r[i].next=i+1; 
    L.r[L.recnum].next = 0;             	//Transform L into a static linked list 
	for(i=0;i<L.keynum;++i) 
	{       	
		//Allocate and collect keywords according to the lowest priority 
		Distribute(L.r,i,f,e);		     	//Allocation of the i-th trip 
		Collect(L.r,i,f,e);					//The i-th collection 
	}//for 
} // RadixSort
 
void print(SLList L)
{  
	//Output static linked list by array sequence number
    int i,j;
    for(i=1;i<=L.recnum;i++)
    {
		for(j=L.keynum-1;j>=0;j--)
			cout<<L.r[i].keys[j];
	    cout<<endl;
    }
}
void Sort(SLList L,int adr[]) 
{ 
	//Find adr[1..L.length], adr[i] is the sequence number of the ith smallest record of the static linked list L
    int i=1,p=L.r[0].next;
    while(p)
    {
		adr[i++]=p;
		p=L.r[p].next;
	}
}
void Rearrange(SLList *L,int adr[])
{ 
	//adr gives the order of the static linked list L, that is, L.r[adr[i]] is the record with the smallest I.
    //This algorithm rearranges L.r according to adr to make it orderly. Algorithm 10.18 (the type of L changes) 
	int i,j,k;
    if(adr[i]!=i)
    {
		j=i;
		(*L).r[0]=(*L).r[i]; //Temporary record (* l) r[i]
		while(adr[j]!=i)
		{ 
			//Adjustment (* l) The record of R [ADR [J]] is in place until adr[j]=i
			k=adr[j];
			(*L).r[j]=(*L).r[k];
			adr[j]=j;
			j=k; //Records are in place in order 
		}
		(*L).r[j]=(*L).r[0];
		adr[j]=j;
    }
}

void main()
{
	SLList l;
	int *adr;
	InitList(&l);
	RadixSort(l);
	adr=new int[l.recnum];
	Sort(l,adr);
	Rearrange(&l,adr);
	cout<<"After sorting(Rearrange records):\n";
	print(l);
} 

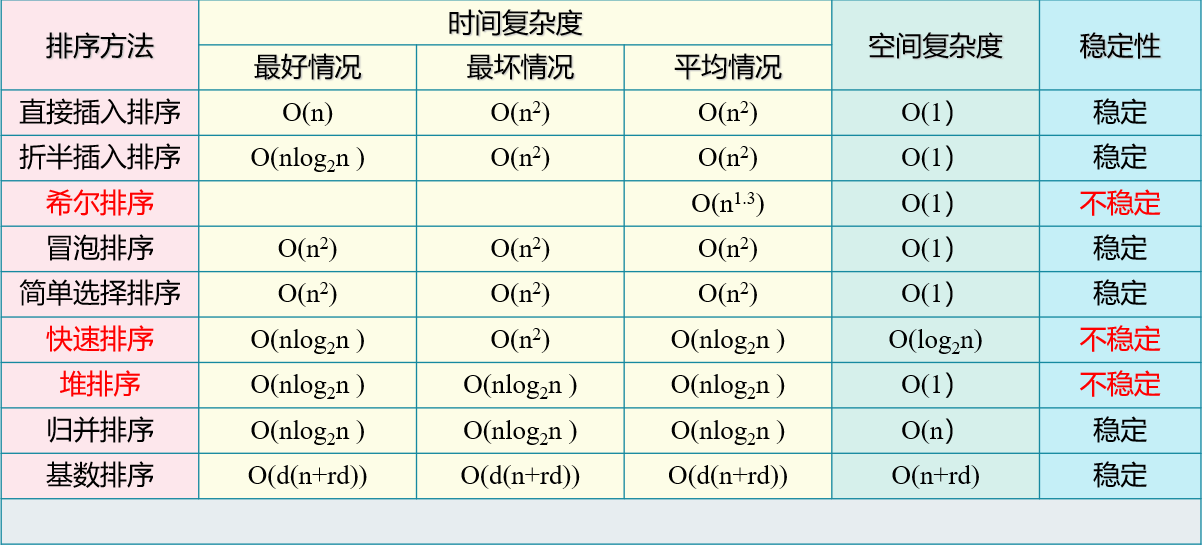
7. Summary

8. Examples and Applications

Realize quick sorting

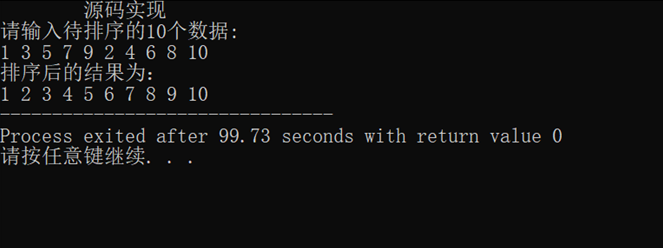
#include<bits/stdc++.h> 
using namespace std;

typedef struct
{
	int key;
	char *otherinfo;
}ElemType;
//Storage structure of sequential table                         
typedef struct
{
    ElemType *r;
    int  length;
}SqList;
//Sort the sub tables of the sequence table and return to the pivot position 
int Division(SqList &L,int low,int high)
{ 
	int pivotkey;
	L.r[0]=L.r[low];
	pivotkey=L.r[low].key;
	while(low<high)
	{
		while(low<high&&L.r[high].key>=pivotkey) --high;
		L.r[low]=L.r[high];
		while(low<high&&L.r[low].key<=pivotkey) ++low;
		L.r[high]=L.r[low];
	}
	L.r[low]=L.r[0];
	return  low;
}
//Quick sort the sequence table 
void QSort(SqList &L,int low,int high)
{  
	int pivotloc;
    if(low<high)
	{										
       pivotloc=Division(L,low,high); 		
       QSort(L,low,pivotloc-1);			
       QSort(L,pivotloc+1,high);
	}
}
//Quick sort 
void QuickSort(SqList &L)
{
   QSort(L,1,L.length);
}
//Enter the data to be sorted								
void Create_Sq(SqList &L)
{
	int i,n;
	cout<<"\t Source code implementation\t"<<endl;
	cout<<"Please enter 10 data to be sorted:\n";
	for(i=1;i<=10;i++)
	{
		cin>>L.r[i].key;
		L.length++;
	}
}
//Output sorted data 
void Show(SqList L)
{
	int i;
	for(i=1;i<=L.length;i++)
		cout<<L.r[i].key<<" ";
}

int main(void)
{
	SqList L;
	L.r=new ElemType[11];
	L.length=0;
	Create_Sq(L);
	QuickSort(L);
	cout<<"The sorted results are:"<<endl;
	Show(L);
}

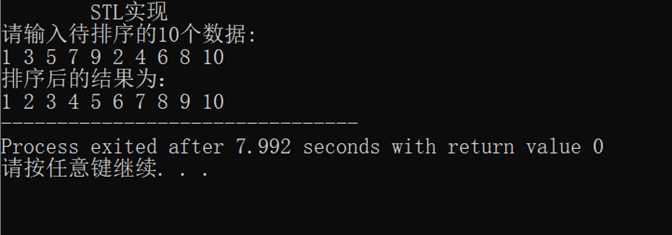
#include<bits/stdc++.h>
using namespace std;

int main(void)
{
	int L[10];
	int i;
	cout<<"\tSTL realization\t"<<endl;
	cout<<"Please enter 10 data to be sorted:\n";
	for(i=0;i<10;i++)
		cin>>L[i];
	sort(L,L+10);
	cout<<"The sorted results are:"<<endl;
	for(i=0;i<10;i++)
		cout<<L[i]<<" ";
	return 0;
 }