1. String

①. Definition of string

String -- a finite sequence composed of zero or more characters. It is a special linear table. Its data element is one character, that is, a linear table with limited content.

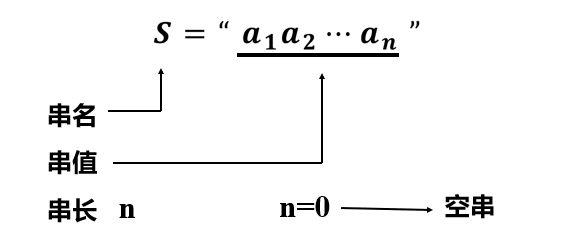
Substring:

A subsequence of any consecutive characters in a string

Main string:

String containing substring

Character position:

Sequence number of characters in the sequence

Substring position:

Represented by the position of the first character of the substring in the main string

Space string:

A string of one or more spaces

Two strings are equal if and only if the values of the two strings are equal. That is, two strings are equal only when their lengths are equal and the characters in each corresponding position are equal. For example, the strings a, b, c, and d in the above example are not equal to each other.

Definition of abstract data type of string:

Similar to linear tables, strings have two basic storage structures: sequential storage and chain storage. However, considering the storage efficiency and the convenience of the algorithm, the string mostly adopts the sequential storage structure.

②. Sequential storage of strings

Similar to the sequential storage structure of linear table, a group of storage units with continuous addresses are used to store the character sequence of string values. Allocate a fixed length storage area for each defined string variable according to the predefined size, and the fixed length array can be described as follows:

typedef struct
{
    char ch[MAXLEN + 1]; // MAXLEN is the maximum length of the string
                         //One dimensional array of storage strings
    int length; //String length
} SString;

In most cases, the operation of string is participated in in the overall form of string, the length difference between string variables is large, and the length of string value changes greatly in the operation, so it is unreasonable to set a fixed size space for string variables. Therefore, it is best to dynamically allocate and release character array space during program execution according to actual needs. In C language, there is a free storage area called "Heap", which can dynamically allocate a storage space required for the actual string length for each newly generated string. If the allocation is successful, a pointer to the starting address is returned as the base address of the string. At the same time, for the convenience of later processing, the agreed string length is also used as a part of the storage structure.

typedef struct
{
    char *ch;   //If the string is not empty, the storage area is allocated according to the string length, otherwise ch is NULL
    int length; //String length
} HString;

③. Chain storage of strings

The insertion and deletion of sequential strings are inconvenient, and a large number of characters need to be moved. Therefore, a single linked list can be used to store strings.

#define CHUNKSIZE 80 / / user definable block size
typedef struct Chunk
{
    char ch[CHUNKSIZE]; //One dimension of storage string
    struct Chunk *next;
} Chunk;

typedef struct
{
    Chunk *head, *tail; //Head pointer and tail pointer of string
    int curlen;         //Current length of string
} LString;

The chain storage structure of string value is convenient for some string operations, such as connection operation, but generally speaking, it is not as flexible as the sequential storage structure. It occupies a large amount of storage and the operation is complex.

④. Pattern matching algorithm of string

The location operation of substring is usually called pattern matching or string matching of string. The main string is called text string and the substring is called pattern string. The purpose of this algorithm is to determine the location (location) of the first occurrence of the condensed substring in the main string. This operation is widely used, such as string matching in search engine, spell check, language translation, data compression and other applications.

BF (brute force) algorithm

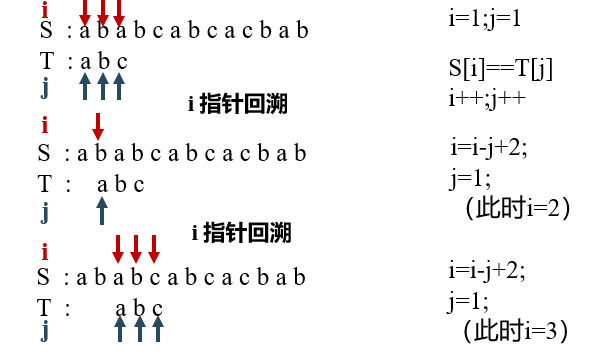
Pattern matching does not necessarily start from the first position of the main string. You can specify the starting position pos in the main string. If the string sequential storage structure is adopted, the matching algorithm that does not depend on other string operations can be written out.

1. The counting pointers i and j are respectively used to indicate the character positions currently to be compared in the main string S and mode T. the initial value of i is POS and the initial value of J is 1.

2. If neither of the two strings is compared to the end of the string, that is, when i and j are less than or equal to the length of S and T respectively, the following operations are performed in the loop:

   - S[i].ch and T[j].ch Compare, if equal, then i and j Respectively indicate the next position in the string and continue to compare subsequent characters;
   
   - If not, the pointer moves back and starts matching again, starting from the next character of the main string( i=i-j+2)Restart the first character of the and mode(j=1 )Compare.
   

3. ③ If J > T.length, it means that each character in mode T is equal to a continuous character sequence in the main string S in turn, the matching is successful, and the sequence number (i-T.length) of the character equal to the first character in mode T in the main string S is returned; Otherwise, the matching is unsuccessful and 0 is returned.

int Index(SString S, SString T, int pos)
{
    i = pos;
    j = 1;                              //initialization
    while (i <= S[0] && j <= T[0])		//Neither string is compared to the tail of the string
    {
        if (S[i] = T[j])
        {
            ++i;
            ++j;
        } //Continue comparing subsequent characters
        else
        {
            i = i - j + 2;
            j = 1;
        } //The pointer moves back and starts matching again
    }
    if (j > T[0])
        return i-T[0]; //Match successful
    else
        return 0; //Match failed
}

BF algorithm example:

/***String matching algorithm***/
#include <cstring>
#include <iostream>
using namespace std;

#define OK 1
#define ERROR 0
#define OVERFLOW -2
typedef int Status;
#define MAXSTRLEN 255 / / you can define the longest string length within 255
typedef char SString[MAXSTRLEN + 1]; // Length of storage string in unit 0

Status StrAssign(SString T, char *chars)
{ //Generates a string T whose value is equal to chars
    int i;
    if (strlen(chars) > MAXSTRLEN)
        return ERROR;
    else
    {
        T[0] = strlen(chars);
        for (i = 1; i <= T[0]; i++)
            T[i] = *(chars + i - 1);
        return OK;
    }
}

// BF algorithm
int Index(SString S, SString T, int pos)
{
    //Returns the position where mode T first appears after the pos character in the main string s. If it does not exist, the return value is 0
    //Where, T is not empty, 1 ≤ pos ≤ StrLength(S)
    int i = pos;
    int j = 1;
    while (i <= S[0] && j <= T[0])
    {
        if (S[i] == T[j])
        {
            ++i;
            ++j;
        } //Continue comparing subsequent characters
        else
        {
            i = i - j + 2;
            j = 1;
        } //The pointer moves back and starts matching again
    }
    if (j > T[0])
        return i - T[0];
    else
        return 0;
    return 0;
} // Index

int main()
{
    SString S;
    StrAssign(S, "bbaaabbaba");
    SString T;
    StrAssign(T, "abb");
    cout << "The main string and substring are in the second" << Index(S, T, 1) << "First match at characters\n";
    return 0;
}

The time complexity of the algorithm is: O (n*m)

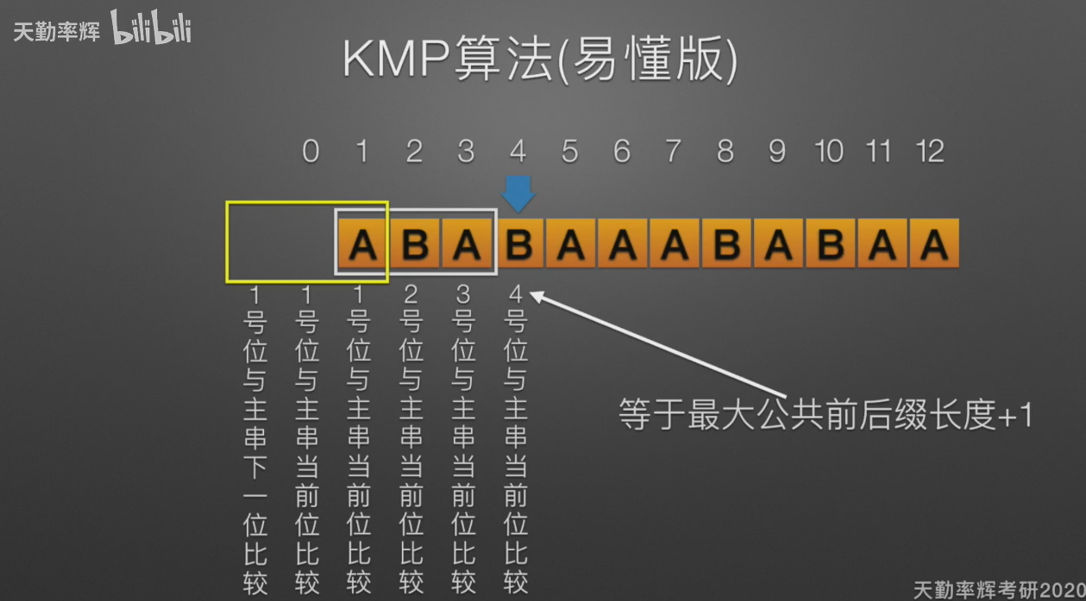
KMP algorithm

This improved algorithm is designed and implemented by Knuth, Morris and Pratt at the same time, so it is called KMP algorithm for short. This algorithm can complete the string pattern matching operation on the time order of O(n + m). The improvement is that whenever there are different character comparisons in the process of one match, there is no need to backtrack the i pointer, but use the obtained "partial match" results to "slide" the pattern to the right as far as possible, and then continue the comparison.

1. The counting pointers i and j are respectively used to indicate the character positions currently to be compared in the main string S and mode T. the initial value of i is POS and the initial value of J is 1.

2. If neither of the two strings is compared to the end of the string, that is, when i and j are less than or equal to the length of S and T respectively, the following operations are performed in the loop:

   - S[i].ch and T[i].ch Compare, if equal, then i and j Respectively indicate the next position in the string and continue to compare subsequent characters;
   - If not, the pointer moves back and starts matching again, starting from the next character of the main string(i=i-j+2)Restart the first character of the and mode(j=1)Compare.
   

3. If J > T.length, it means that each character in mode T is equal to a continuous character sequence in the main string S in turn, the matching is successful, and the sequence number (i-T.length) of the character equal to the first character in mode T in the main string S is returned; Otherwise, the matching is unsuccessful and 0 is returned.

If you are interested in the idea of the algorithm, you can watch the explanation video of tianqin open class. Personally, I think the explanation is relatively thorough:

"Tianqin open class" KMP algorithm easy to understand version

It is briefly described below:

The function of kmp algorithm is to quickly find the desired substring from a main string. kmp algorithm can only move the mode string backward without backtracking the comparison pointer.

Find out the common prefix that is the longest but not longer than the left end of the pattern string mismatch, and directly move the pattern string so that the prefix directly comes to the suffix position.

int Index_KMP(SString S, SString T, int pos)
{
    i = pos;
    j = 1;                                 //initialization
    while (i <= S.length && j <= S.length) //Neither string is compared to the tail of the string
    {
        if (j == 0 || S[i] == T[j])
        {
            ++i;
            ++j;
        } //Continue comparing subsequent characters
        else
        {
            j = next[j];
        } //The mode string moves to the right
    }
    if (j > T[0])
        return i - T[0]; //Match successful
    else
        return 0; //Match failed
}

void get_next(SString T, int next[])
{ //Find the next function value of the mode string T and store it in the array next
    i = 1;
    next[1] = 0;
    j = 0;
    while (i < T[0])
    {
        if (j == 0 || T[i])
        {
            ++i;
            ++j;
            next[i] = j;
        }
        else
        {
            j = next[j];
        }
    }
}

KMP algorithm example:

/***String matching algorithm***/
#include <cstring>
#include <iostream>
using namespace std;

#define OK 1
#define ERROR 0
#define OVERFLOW -2
typedef int Status;
#define MAXSTRLEN 255 / / you can define the longest string length within 255
typedef char SString[MAXSTRLEN + 1]; // Length of storage string in unit 0

Status StrAssign(SString T, char *chars)
{ //Generates a string T whose value is equal to chars
    int i;
    if (strlen(chars) > MAXSTRLEN)
        return ERROR;
    else
    {
        T[0] = strlen(chars);
        for (i = 1; i <= T[0]; i++)
            T[i] = *(chars + i - 1);
        return OK;
    }
}
//Algorithm 4.3 calculate the value of next function
void get_next(SString T, int next[])
{ //Find the next function value of the mode string T and store it in the array next
    int i = 1, j = 0;
    next[1] = 0;
    while (i < T[0])
        if (j == 0 || T[i] == T[j])
        {
            ++i;
            ++j;
            next[i] = j;
        }
        else
            j = next[j];
} // get_next

// KMP algorithm
int Index_KMP(SString S, SString T, int pos, int next[])
{ // KMP algorithm for finding the position of T after the pos character in the main string S by using the next function of mode string t
    //Where, T is not empty, 1 ≤ pos ≤ StrLength(S)
    int i = pos, j = 1;
    while (i <= S[0] && j <= T[0])
        if (j == 0 || S[i] == T[j]) // Continue to compare subsequent words
        {
            ++i;
            ++j;
        }
        else
            j = next[j]; // The mode string moves to the right
    if (j > T[0])        // Match successful
        return i - T[0];
    else
        return 0;
} // Index_KMP

int main()
{
    SString S;
    StrAssign(S, "aaabbaba");
    SString T;
    StrAssign(T, "abb");
    int *p = new int[T[0] + 1]; // Generate next array of T
    get_next(T, p);
    cout << "The main string and substring are in the second" << Index_KMP(S, T, 1, p) << "First match at characters\n";
    return 0;
}

Time complexity: O (n+m)

2. Array

①. Definition of array

An array is an ordered set composed of data elements of the same type. Each element is called an array element. Each element is constrained by n(n ≥ 1) linear relationships. The sequence numbers i1, i2,..., in of each element in n linear relationships are called the subscript of the element, and the data element can be accessed through the subscript. Because each element in the array is in n(n ≥ 1) relationships, it is called an n-dimensional array. Array can be regarded as the generalization of linear table. Its characteristic is that the elements in the structure can be data with a certain structure, but they belong to the same data type.

②. Sequential storage of arrays

Because the array is generally not inserted or deleted, that is to say; Once the array is established, the number of data elements in the structure and the relationship between elements will not change. Therefore, it is more appropriate to use sequential storage structure to represent arrays.
Two dimensional arrays can be stored in two ways: one is based on column order; One is the storage mode with row order as the main order.

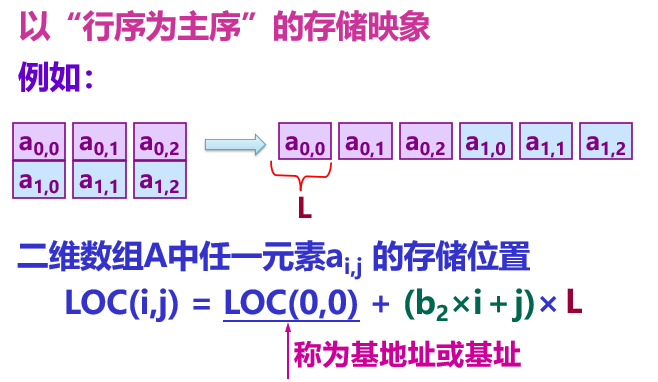
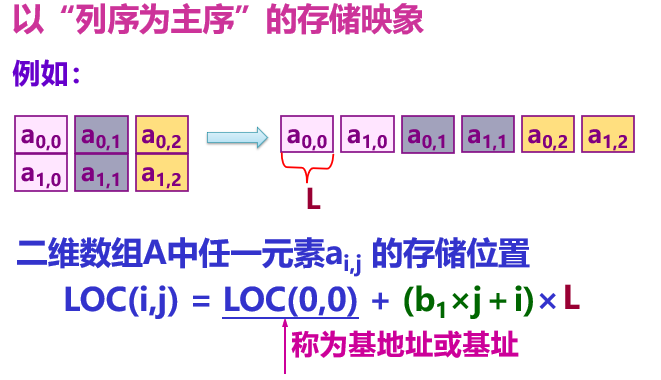
Sequential storage of 3D arrays:

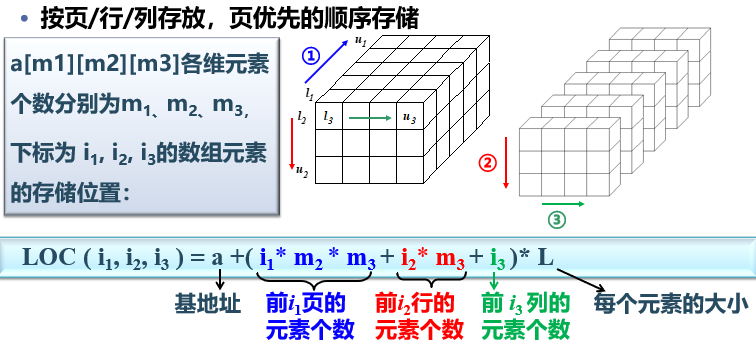
③. Compressed storage of special matrix

Special matrix: the distribution of elements with the same value or 0 elements in the matrix has a certain law. Such as: symmetric matrix, triangular matrix, diagonal matrix, etc.

Compressed storage: compressed storage means that only one storage space is allocated to multiple elements with the same value, and no storage space is allocated to zero elements. The purpose is to save a lot of storage space.

What kind of matrix can be compressed?
Special matrix, sparse matrix, etc.

symmetric matrix

If the elements in the nth order matrix A satisfy AIJ = Aji, 1 ≤ i, j ≤ n, it is called the nth order symmetric matrix. For A symmetric matrix, A storage space can be allocated for each pair of symmetric elements, and n2 elements can be compressed and stored in the space of n(n+1)/2 elements without losing generality. The elements in its lower triangle (including diagonal) can be stored in row order as the main order.
Assuming that one-dimensional array sa[r(n+1)/2] is used as the storage structure of n-order symmetric matrix A, there is a one-to-one correspondence between sa[k] and matrix element aj:

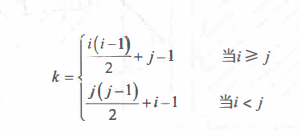
Triangular matrix

Divided by the main diagonal, the triangular matrix can be divided into upper triangular matrix and lower triangular matrix. The upper triangular matrix refers to the n-order matrix whose elements in the lower triangular matrix (excluding diagonal) are constant c or zero, and the lower triangular matrix is the opposite. When the triangular matrix is compressed and stored, in addition to storing only the elements in its upper (lower) triangle like the symmetric matrix, a storage space of storage constant c can be added.

Upper triangular matrix
The corresponding relationship between sa[k] and matrix element aij is:

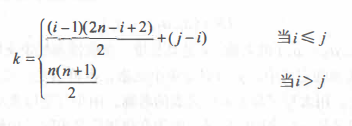
Lower triangular matrix
The corresponding relationship between sa[k] and matrix element aij is:

Diagonal matrix

All non-zero elements of the diagonal matrix are concentrated in the banded area centered on the main diagonal, that is, except the elements on the main diagonal and directly on several diagonals above and below the diagonal, all other elements are zero.

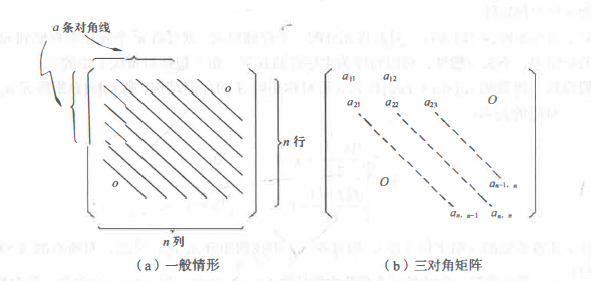
3. Generalized table

①. Definition of generalized table

Generalized table: a finite sequence composed of n (≥ 0) table elements, recorded as LS = (a1, a2,..., an). LS is the table name and ai is the table element. It can be a table (called a sub table) or a data element (called an atom). N is the length of the table, and a generalized table with n=0 is called an empty table.

GetHead(L): the first element of a non empty generalized table, which can be an atom or a sub table.
GetTail(L): a non empty generalized table consisting of all other elements except the header element. The end of the table must be a table.

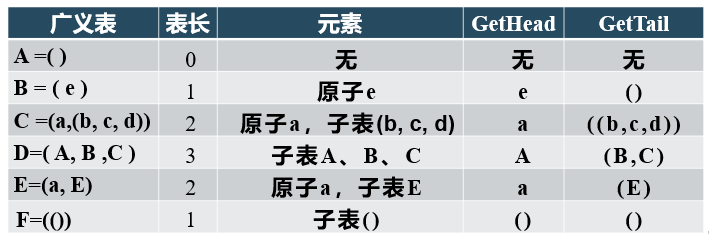
②. Storage structure of generalized table

Because the data elements in the generalized table can have different structures (either atoms or lists), it is difficult to express them with sequential storage structure, and the chain storage structure is usually used.

Storage structure of head and tail linked list

Because the data elements in the generalized table may be atoms or generalized tables, two kinds of nodes are needed: one is the table node, which is used to represent the generalized table; One is the atomic node, which is used to represent the atom. It is learned from the previous section that if the generalized table is not empty, it can be decomposed into header and footer. Therefore, a pair of determined header and footer can uniquely determine the generalized table. A table node can be composed of three fields: flag field, pointer field indicating the header and pointer field indicating the footer. Atomic nodes only need two domains: Flag domain and value domain.

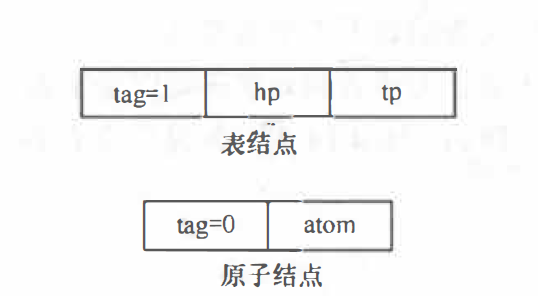
typedef enum
{
    ATOM,
    LIST
} ElemTag;
// ATOM==0: atom, LIST==1: sub table
typedef struct GLNode
{
    ElemTag tag; //The common part is used to distinguish atomic nodes and table nodes
    union        //Joint part of atomic node and table node
    {
        AtomType atom; // atom is the value domain of the atomic node, and AtomType is defined by the user
        struct
        {
            struct GLNode *hp, *tp;
        } ptr;
        // ptr is the pointer field of the table node, PRT HP and ptr TP points to the header and footer respectively
    };
} * GList, GLNode; /* Generalized table type */

Storage structure of extended linear linked list

In this structure, both atomic nodes and table nodes are composed of three domains

typedef struct glnode
{
    int tag; // 0 atomic node; 1 sub table node
    union
    {
        atomtype atom;     //Value range of atomic node
        struct glnode *hp; //Sub table header pointer
    } struct glnode *tp;   //Next element pointer
} * glist;

4. Summary

1. String is a linear table with limited content, which limits the elements in the table to characters. String has two basic storage structures: sequential storage and chain storage, but most of them use sequential storage structure. The common algorithm of string is pattern matching algorithm, which mainly includes BF algorithm and KMP algorithm. BF algorithm is simple to implement, but it has backtracking, low efficiency and time complexity of O(m) × n). KMP algorithm improves BF algorithm, eliminates backtracking and improves efficiency. The time complexity is O(m+n).

2. Multidimensional array can be regarded as the generalization of linear table. Its characteristic is that the elements in the structure can be data with a certain structure, but they belong to the same data type. An n-dimensional array is essentially a combination of n linear tables, and each dimension is a linear table. Arrays generally adopt sequential storage structure, so when storing multi-dimensional arrays, they should first be determined and converted into one-dimensional structure, including "row" conversion and "column" conversion. Matrices in scientific and engineering calculations are usually represented by two-dimensional arrays. In order to save storage space, several common forms of special matrices, such as symmetric matrix, triangular matrix and diagonal matrix, can be compressed during storage, that is, multiple elements with the same value are allocated only one storage space, and zero elements are not allocated space.

3. Generalized table is another generalized form of linear table. The elements in the table can be a single element called atom or a sub table, so linear table can be regarded as a special case of generalized table. The structure of generalized table is quite flexible. Under some premise, it can be compatible with various common data structures such as linear table, array, tree and directed graph. The common operations of generalized table include taking the header and taking the footer. The generalized list usually adopts the chain storage structure: the storage structure of head and tail linked list and the storage structure of extended linear linked list.

5. Examples and Applications