1, Definition and characteristics of linear table

1. Definitions

A finite sequence consisting of n elements with the same data characteristics is called a linear table
N is the length of the linear table. When n=0, it is an empty table

2. Features

(non empty linear table or linear structure)

1. Unique "first" data element
2. Unique "last" data element
3. Except for the first, each data element has only one precursor
4. Except the last one, there is only one successor

3. Type definition

(see specific procedure exercises)

2, Sequential representation and implementation of linear table

Sequential table: a group of storage units with continuous addresses are used to store the data elements of the linear table in turn;
Features: logically adjacent, physically adjacent
Storage location of the ith element: LOC (ai) = LOC (a1) + (i-1) * l
(let each element occupy l storage units)
advantage:

• High storage density (storage capacity of node itself / storage capacity of node structure)
• Any element in the table can be accessed at random
  Disadvantages:
• When inserting or deleting an element, a large number of elements need to be moved
• Waste of storage space
• It belongs to static storage form, and the number of data elements cannot be expanded freely

Basic operation and implementation of sequence table

initialization

Status	InitList(SqList	&L)
{//Construct an empty sequence table L
	L.elem=new	ElemType[MAXSIZE];	//Allocate an array space of MAXSIZE for the sequential table 
	if(!L.elem)exit(OVERFLOW);		//Storage allocation failed exit 
	L.length=0;						//Empty table length is 0 
	return	OK; 
 } 

Value
Obtain the value of the ith element in the sequence table according to the specified position sequence number i.
The characteristics of random storage are directly obtained by array subscript positioning, and the elem[i-1] unit stores the ith element

Status	GetElem(SqList	L,int	i,ElemType	&e)
{
	if(i<1||i>L.length)	return	ERROR;	//Judge whether the i value is reasonable. If it is unreasonable, error will be returned 
	e=L.elem[i-1]；		//The elem[i-1] unit stores the ith data element 
	return	OK; 
}

The time complexity of the sequential table value algorithm is O (1)
lookup
Finds the first element in the order table equal to e according to the specified element value E

int	LocateElem(SqList	L,ElemType	e)
{//Find the data element with the value e in the sequence table L and return its sequence number
	for(i-0;i<L.length;i++)
		if(L.elem[i]==e )	return	i+1;	//If the search is successful, the sequence number i+1 is returned 
	return	0;//Find failed, return 0 
}

Average search length ASL=(n+1) / 2
Average time complexity: O (n)
insert
Insert a new data element E at the ith position of the table to change the linear table with length n into a linear table with length n+1. Generally, it is necessary to move back one position from the last element, i.e. the nth element, to the ith (n-i+1 in total)

Status	ListInsert(SqList	&L,ElemType	e)
{//Insert a new element e at the ith position in the sequence table L, and the legal range of i value is 1 < = i < = L.Length + 1
	if(i<1)||(i>L.length+1)	return	ERROR;//Illegal i value
	if(L.length==MAXSIZE)	retur	ERROR;//The current storage space is full
	for(j=L.length-1;j>=i-1;j--)
	L.elem[j+1]=L.elem[j];//Move back the element at and after the insertion position
	L.elem[i-1]=e;//Put the new element e in position i
	++L.length;//Table length plus 1
	return	OK;
}

Average times Eins=n/2
Average time complexity: O (n)
delete
Delete the ith element of the table, so that the linear table with length n becomes a linear table with length n-1. Generally, it is necessary to move the i+1 to n (n-i in total) forward one position in turn (i=n, no need to move)

Status	ListDelete(SqList	&L,int	i)
{//Delete the ith element in the sequence table L, and the legal range of i value is 1 < = i < = L.Length
	if(i<1)||(i>L.length)	return	ERROR;//Illegal i value
	for(j=i;j<=L.length-1;j++)
	L.elem[j-1]=L.elem[j];//Move element forward after deleted element 
	--L.length;//Table length minus 1
	return	OK;
}

Average times Edel = (n-1) / 2
Average time complexity: O (n)

3, Chain representation and implementation of linear list

1. Definition and representation of single linked list

The single linked list is uniquely determined by the header pointer

typedef	struct	LNode
{
	ElemType	data;	//Data field of node 
	struct	LNode	*next;//Pointer field of node 
}LNode,*LinkList;//LinkList is the pointer type to the structure LNode 

LinkList and LNode are of the same structure pointer type and are essentially equivalent
It is customary to define a single linked list with LinkList, and LNode defines pointer variables pointing to any node in the single linked list
LinkList L/LNode *p refers to the linked list as Table L, and l is named after the header pointer

• Initial node: the node of the first data element a1 stored in the linked list
• Head node: a node attached before the initial node. The pointer field points to the initial node
• Header pointer: pointer to the first node in the linked list
  Increase head node action
• To facilitate the processing of the initial node, the address of the initial node is saved in the pointer field of the head node, and the operation of the first bit data element in the linked list is the same as others without special processing;
• It is convenient for the unified processing of null and non null tables. When there is no header node, when the length of the single linked table is null, the header pointer is null (L==NULL)
  Whether the linked list is empty or not, the head pointer refers to the non null pointer to the head node.
  If P - > data = AI, then p - > next - > data = AI + 1 Single linked list is a non random access storage structure, which must be searched in the chain from the pointer, which is called sequential access access structure.

2. Implementation of basic operation of single linked list

initialization
Construct an empty table

Status	InitList(LinkList	&L)
{//Construct an empty single linked list L
	L=new	LNode;//Generate a new node as the head node, and point to the head node with the head pointer L
	L->next=NULL;//The pointer field of the header node is set to null
	return	ok； 
 } 

Value
Unlike the sequential list, the logically adjacent nodes are not stored in the physically adjacent cells and cannot be accessed randomly like the sequential list. They can only be accessed from the first node of the chain list down the chain domain one by one

Status	GetElem(LinkList	L,int	i;ElemType	&e)
{//In the single linked list L of the head node, obtain the value of the element with sequence number i, and use e to return the value of the ith data element in L 
	p=L->next;j=1;//Initialization, p points to the initial node, and the initial value of counter j is assigned 1
	while(p&&j<i)//Scan the chain domain backward until p is empty or p points to the ith element
	{
		p=p->next;//p points to the next node
		++j;//Counter j is incremented by 1 accordingly 
	 } 
	 if(!p||j>1)return	ERROR;//Illegal i value i > n or i < = 0
	 e=p->data;//Take the data field of the ith node 
	return	ok； 
 } 

ASL=(n-1)/2
Average time complexity: O(n)
lookup
Similar to the sequence table, this comparison starts from the initial node

LNode	*LocateElem(LinkList	L,ElemType	e)
{//Find the element with value e in the single linked list L of the leading node
	p=L->next;//Initialization, p points to the initial node
	while(p&&p->data!=e)//Scan the chain domain backward until P is empty or the data domain of the node referred to by P is equal to e
		p=p->next;//p points to the next node
	return	p;//The node address p with the return value of e is found successfully, and the node address p with the return value of e is NULL if the search fails 
 } 

Similar to sequence table
Average time complexity: O(n)
insert
s->next=p->next;p->next=s;

Status	ListInsert(LinkList	&L,int	i,ElemType	e)
{//Insert a new node with a value of e at the ith position in the single linked list L of the leading node
	p=L;j+0;
	while(p&&(j<i-1)) 
	{p=p->next;++j;}//Find the i-1 node, and p points to it 
	if(!p||j>i-1)	return ERROR;//i> N + 1 or I < 1
	s=new	LNode;//Generate new node * s
	s->data=e;//Set the data field of node * S to e
	s->next=p->next;//Point the pointer field of node * s to node ai
	p->next=s;//Point the pointer field of node * p to node * s
	return	OK;	
}

You do not need to move elements like the sequence table, but you need to find the i-1 node before inserting elements before the i-th node
Average time complexity: O (n)
delete
p->next=p->next->next; Before modifying the pointer, another pointer q shall be introduced to temporarily save the address of b for release

Status	ListDelete(LinkList	&L,int	i)
{//Delete the ith element in the single linked list L of the leading node 
	p=L;j=0;
	while((p=p->next)&&(j<i-1)) //Find the i-1 node, and p points to it 
	{p=p->next;++j;}
	if(!(p->next)||(j>i-1))	return ERROR;//i> N or I < 1, the deletion position is unreasonable 
	q=p->next;//Temporarily save the address of the deleted node for release
	p->next=q->next;//Change the pointer field of the predecessor node of the deleted node
	delete	q;//Free up space for deleting nodes 
	return	OK;	
}

Average time complexity: O (n)
Create single linked list

• Forward interpolation

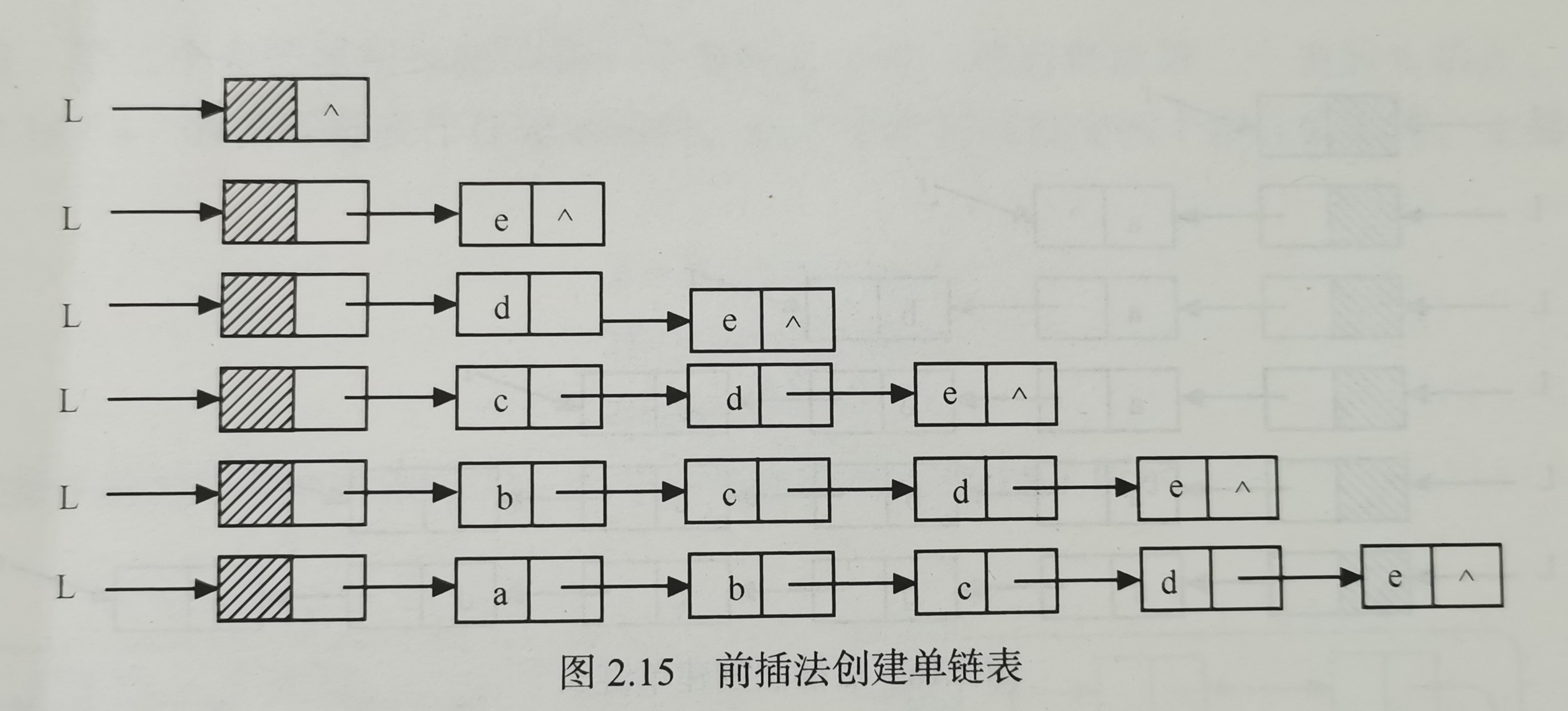
void	CreateList_H(LinkList	&L,int	n)
{//Input the values of n elements in the reverse bit order to establish the single linked list L of the leading node
	L=new	LNode;
	L->next=NULL;//First, create an empty linked list of the leading node
	for(i=0;i<n;++i)
	{
		p=new	LNode;//Generate new node * p
		cin>>p->next;//The input element value is assigned to the data field of the new node * p
		p->next=L->next;L->next=p;//Insert the new node * p after the head node 
	} 
 } 

Average time complexity: O (n)

• Back interpolation
  

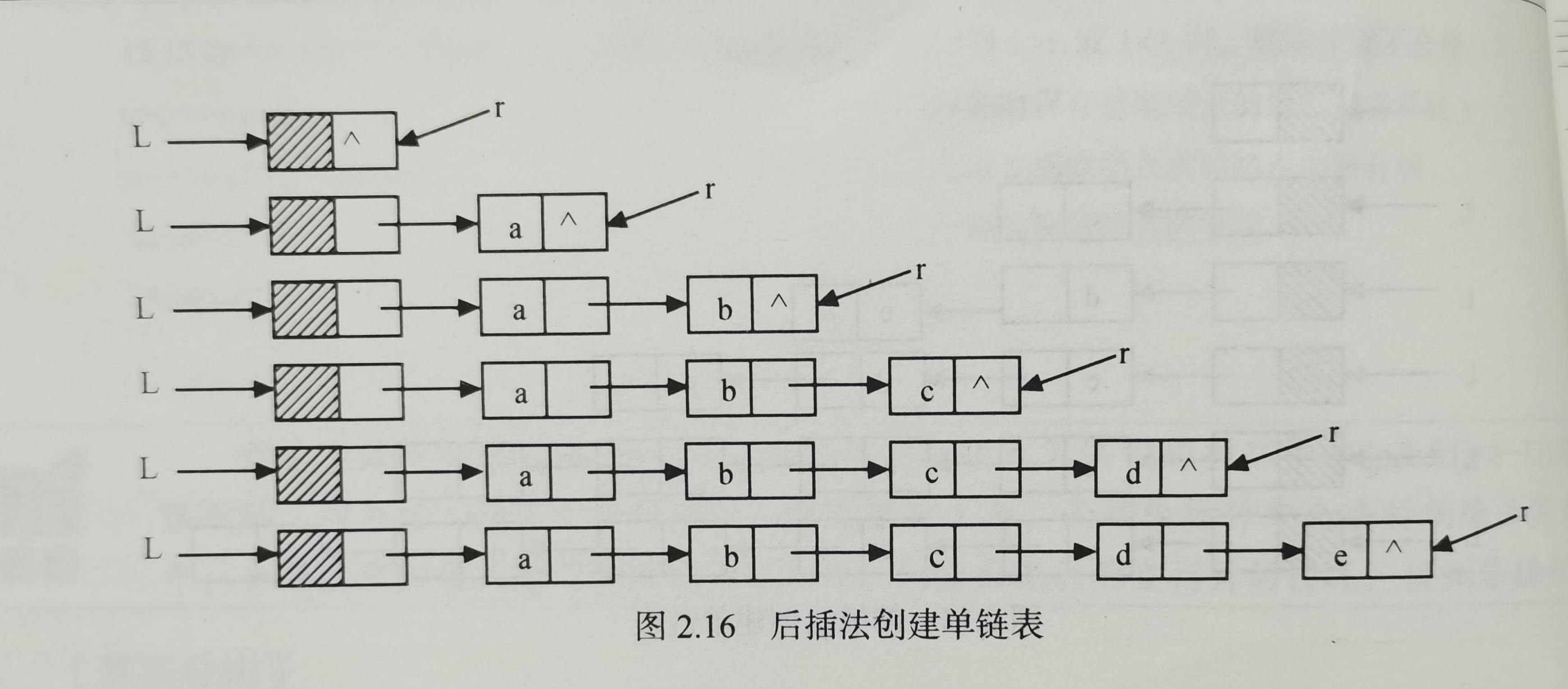
void	CreateList_R(LinkList	&L,int	n)
{//Enter the values of n elements in the positive bit order to establish the single linked list L of the leading node
	L=new	LNode;
	L->next=NULL;//First, create an empty linked list of the leading node
	r=L;//The tail pointer r points to the head node 
	for(i=0;i<n;++i)
	{
		p=new	LNode;//Generate new node * p
		cin>>p->next;//The input element value is assigned to the data field of the new node * p
		p->next=NULL;r->next=p;//Insert the new node * p after the tail node * r 
		r=p;//r points to the new tail node * p 
	} 
 } 

Average time complexity: O (n)

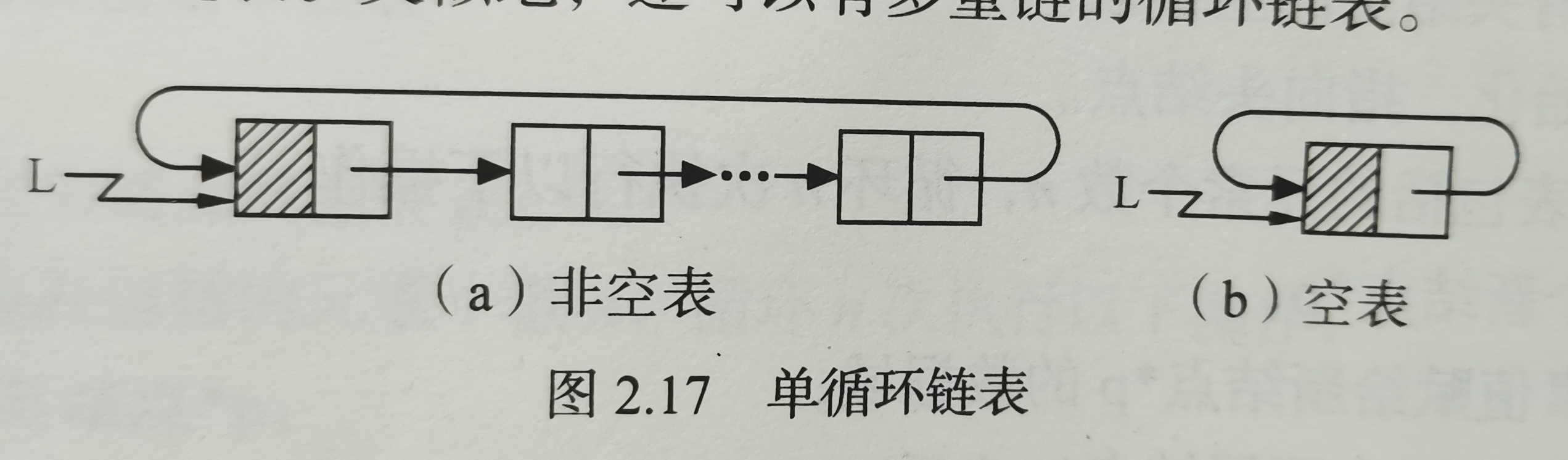
3. Circular linked list

Features: the pointer field of the last node in the list points to the head node, and the whole linked list forms a ring;
Difference from single linked list: single linked list criteria: P= Null or P - > next= Null, the circular single linked list is p= L or P - > next= L

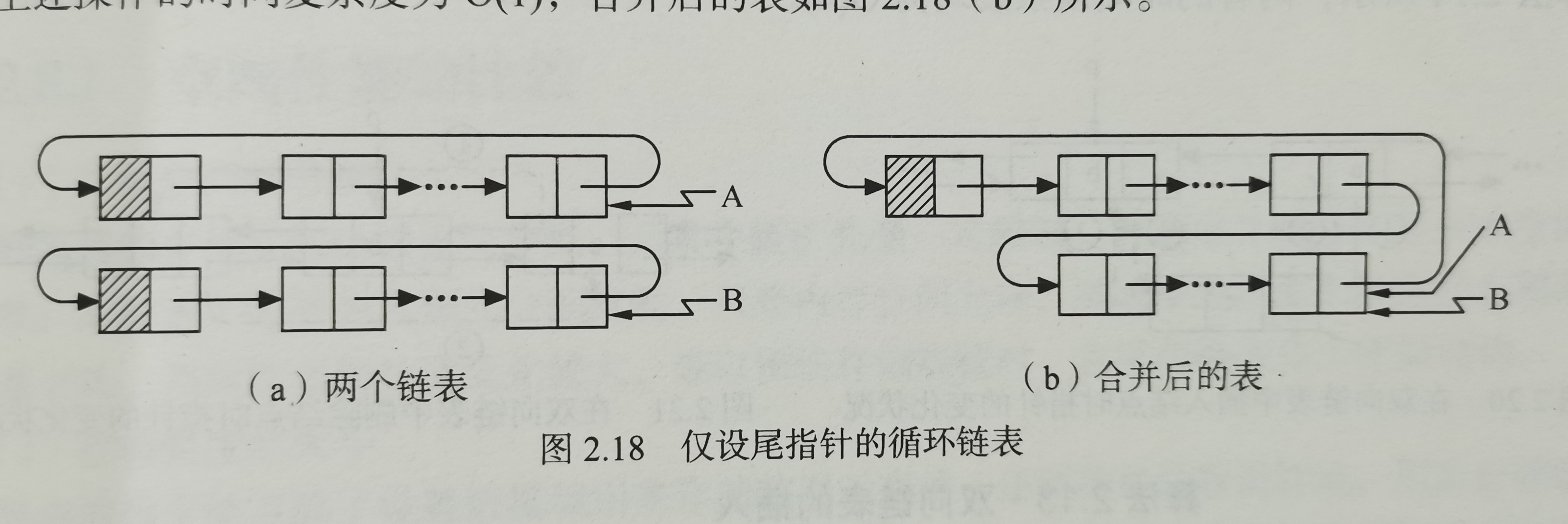
Merge two linear tables into one

p=B->next->next;
B->next=A->next;
A->next=p; 

Time complexity: O (1)

4. Two way linked list

Overcome the unidirectionality of single linked list
Two pointer fields

typedef	stryct	DuLNode
{
	ElemType	data;//Data domain
	struct	DuLNode	*prior;//Direct precursor
	struct	DuLNode	*next;//Direct successor 
 } DuLNode,*DuLinkList; 

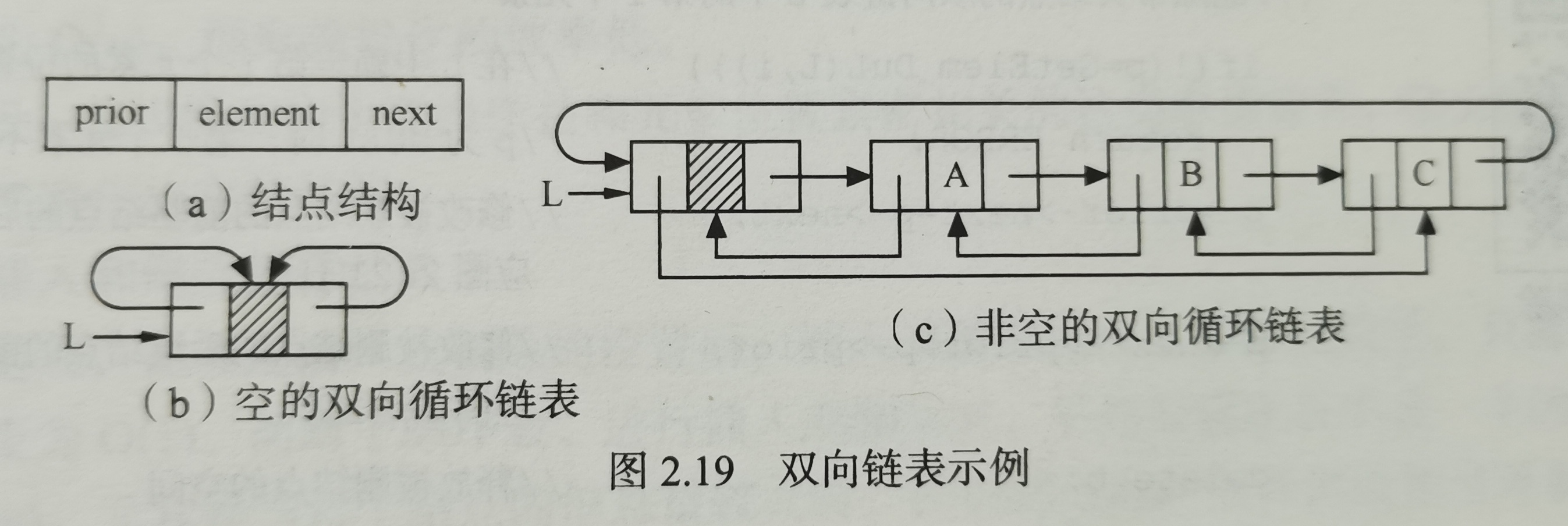
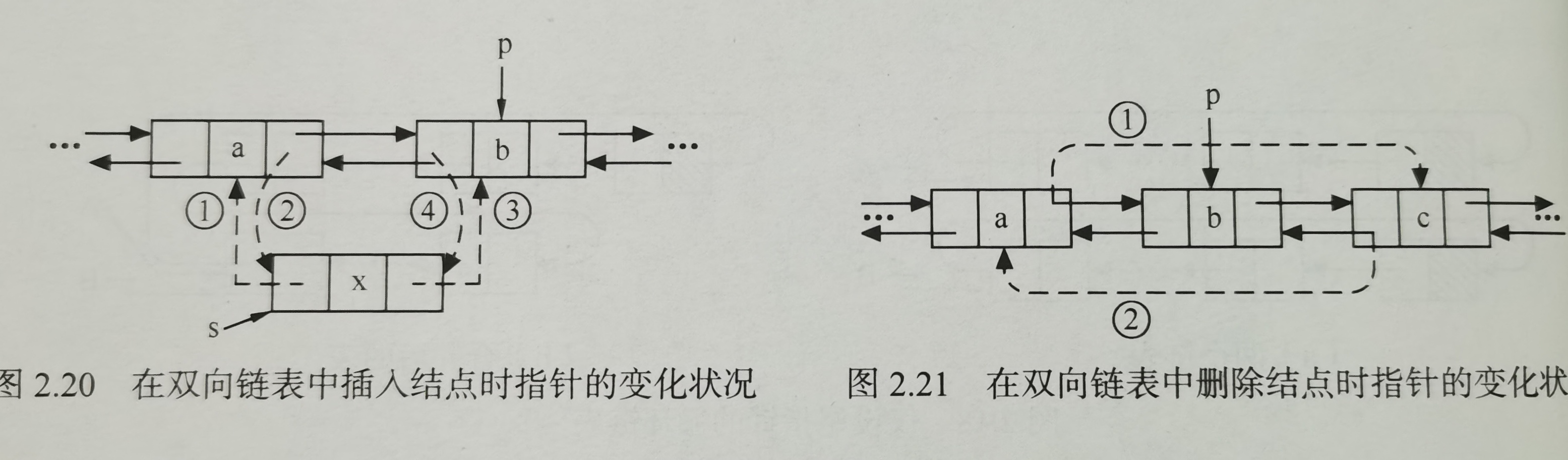
Four pointers need to be modified when inserting a node and two pointers need to be modified when deleting a node
insert

Status	ListInsert_DuL(DuLinkList	&L,int	i,ElemType	e)
{//Insert element e before the ith position in the bidirectional linked list L of the leading node
	if(!(p=GetElem_DuL(L,i)))//Determine the position pointer p of the ith element in L
	return	ERROR;//When p is NULL, the ith element does not exist
	s=new	DuLNode;//Generate new node * s
	s->data=e;//Set the new node * s data field as S
	s->prior=p->prior;//Insert the new node * s into L, corresponding to figure 2.20 one
	p->prior->next=s;//Corresponding to 2.20 two
	s->next=p;//Corresponding to 2.20 three
	p->prior=s;//Corresponding to 2.20 four
	return	OK; 
}

delete

Status	ListDelete_DuL(DuLinkList	&L,int	i)
{//Delete the ith element in the bidirectional linked list L of the leading node
	if(!(p=GetElem_DuL(L,i)))//Determine the position pointer p of the ith element in L
	return	ERROR;//When p is NULL, the ith element does not exist
	p->prior->next=p->next;//Modify the subsequent pointer of the predecessor node of the deleted node, corresponding to 2.21 one
	p->next->prior=p->prior;//Modify the precursor pointer of the successor node of the deleted node, corresponding to 2.21 two 
	delete	p;//Free up space for deleted nodes 
	return	OK; 
}

The time complexity of both is O (n)

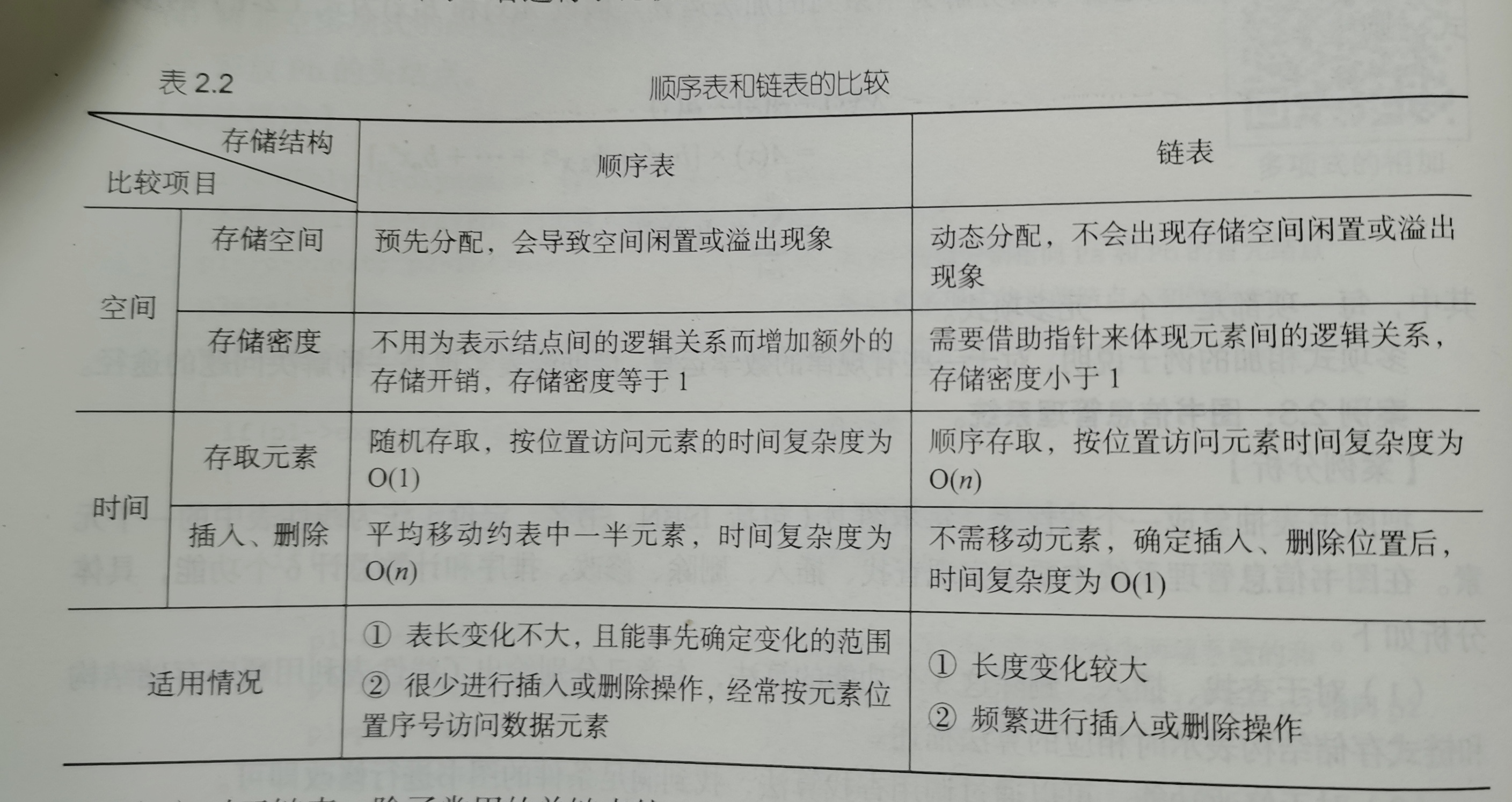
4, Comparison of sequential list and linked list

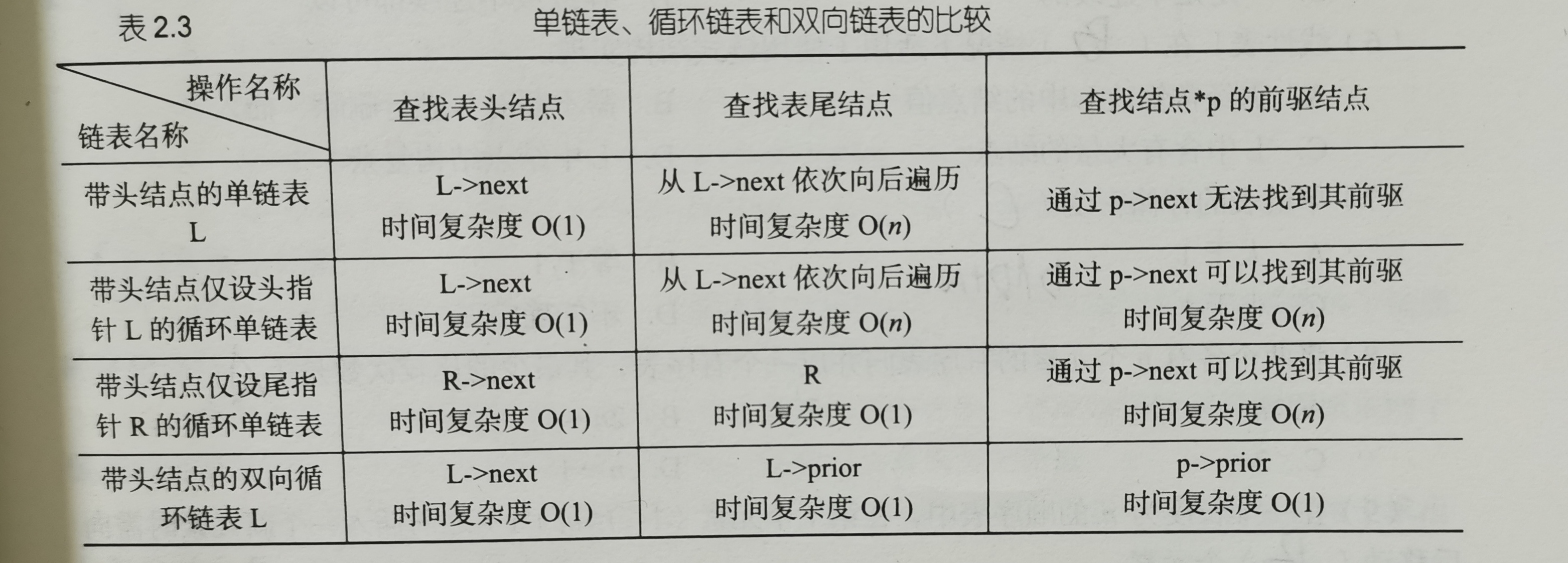
5, Application of linear table

1. Consolidation of linear tables

Time complexity: O (m*n)

2. Consolidation of ordered tables

• Sequential table:
  Time complexity: O(m+n)
  Space complexity: O(m+n)
• Linked ordered list:
  Time complexity: O(m+n)
  Space complexity: O(1)