Stack

Basic concepts

A stack is a linear table that only allows insertion or deletion at one end.

Important terms:

Stack top, bottom, empty stack, last in first out (LIFO)

Sequential stack

#define MAXSIZE 20 / / define the maximum number of stack elements
typedef struct {
	int data[MAXSIZE];
	int top; //Stack top pointer
} SqStack;

Basic operation of sequential stack

//Initialization stack
void initStack(SqStack *s) {
	s->top = -1;
}

//Determine whether the stack is empty
bool isStackEmpty(SqStack *s) {
	if (s->top == -1) {
		return true; //Stack empty
	}
	return false;
}

//Enter the stack
bool push(SqStack *s, int e) {
	if (s->top == MAXSIZE - 1) {
		return false; //If the stack is full, the insertion fails
	}
	s->top++;
	s->data[s->top] = e;
	printf("%d Stack successfully\n", s->data[s->top]);
	return true;
}

//Out of stack
bool pop(SqStack *s, int *e) {
	if (s->top == -1) {
		return false;
	}
	*e = s->data[s->top];
	s->top--;
	printf("%d Stack successfully\n", *e);
	return true;
}

//Stack empty
void emptyStack(SqStack *s) {
	s->top = -1;
}

//Stack destruction
void destroyStack(SqStack *s) {
	free(s);
}

int main() {
	SqStack s;
	initStack(&s);
	isStackEmpty(&s);
	int a = 10;
	int b = 13;
	int c = 15;
	int d;
	push(&s, a);
	push(&s, b);
	push(&s, c);
	pop(&s, &d);
	emptyStack(&s);
	destroyStack(&s);
	return 0;
}

Chain stack

typedef struct Linknode {
	int data;//Data domain
	struct Linknode *next;//Pointer field
}*LiStack;

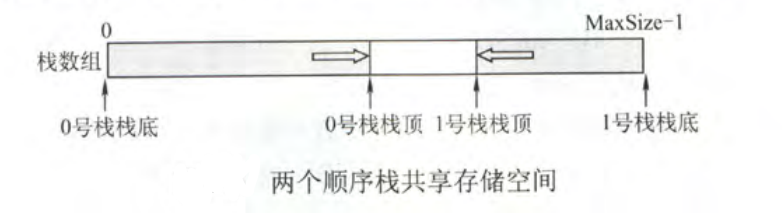
Shared stack

The stack top pointers of both stacks point to the stack top element. Stack 0 is empty when top0=-1, and stack 1 is empty when top1=MaxSize.

Only when two stack top pointers are adjacent (top1-top0=1), it is judged that the stack is full.

When stack 0 enters the stack, top0 first adds 1 and then assigns value; when stack 1 enters the stack, topl first subtracts 1 and then assigns value; When it comes out of the stack, it is just the opposite.

Shared stack is to make more effective use of storage space. The space of the two stacks is adjusted to each other. Overflow occurs only when the whole storage space is occupied.

The time complexity of accessing data is O (1), so it has no impact on the access efficiency.

Cartland style

If the stacking sequence of n elements is: 1, 2, 3, 4,..., N, how many out of stack sequences are there.

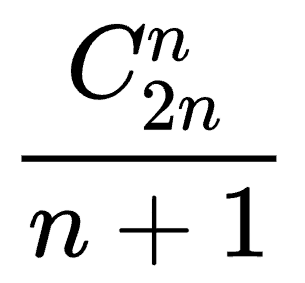
queue

Basic concepts

Queue: queue is called queue for short. It is also a linear table with limited operations. It is only allowed to insert at one end of the table and delete at the other end of the table. Inserting elements into the queue is called in or out of the queue; deleting elements is called out of the queue or out of the queue.

Its operation characteristic is First In First Out (FIFO), so it is also called First In First Out linear table.

Front: the end that can be deleted, also known as the head of the team.

Rear: the end that allows insertion.

Empty queue: an empty table without any elements.

Sequential storage of queues (false overflow)

structure type

#define MaxSize 50
typedef struct {
	int data[MaxSize];
	int front;//Team leader
	int rear;//Team tail
} SqQueue;

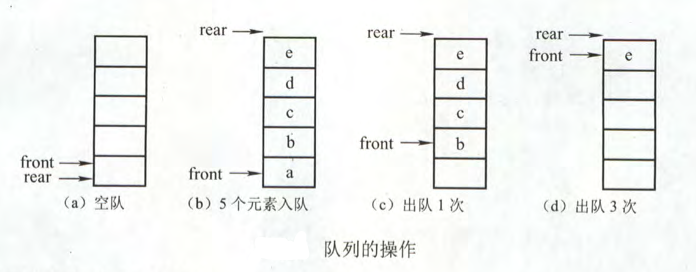
Initial state (team empty condition): q.frontq.real0.

Queue entry operation: when the queue is not satisfied, first send the value to the queue end element, and then add 1 to the queue end pointer.

Out of queue operation: when the queue is not empty, first take the value of the queue head element, and then add 1 to the queue head pointer.

As shown in figure a, the initial state of the queue is q.frontq If real = 0 is true, this condition can be used as a condition for queue empty judgment. However, q.realmaxsize cannot be used as a condition for the queue to be full. In Figure d, there is only one element in the queue, but this condition is still met. At this time, there is an "upper overflow" in the queue, but this overflow is not a real overflow. There is still an empty position in the data array where elements can be stored, so it is a * * "false overflow" * *.

Circular queue

structure type

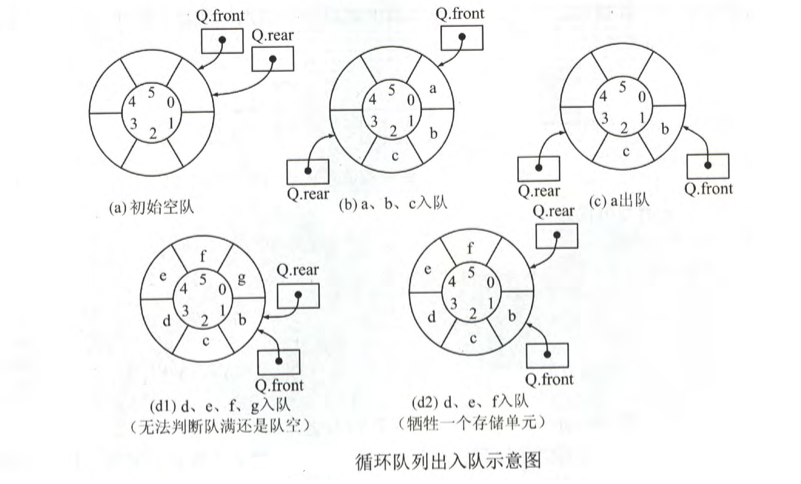
In order to solve the false overflow of the queue, the division and remainder operation can be used to logically turn the linear array into a circular queue.

Initial: Q.front=Q.rear=0

Queue head pointer 1: Q.front=(Q.front+1)%MaxSize

End of queue pointer 1: Q.rear=(Q.rear+1)%MaxSize

Queue length: (Q.rear+MaxSize-Q.front)%MaxSize

There are three ways to solve the Q.front=Q.rear condition when the queue is empty and full:

1. Sacrifice a unit. (more used) full team: (Q.rear+1)%MaxSize=Q.front

2. Add a counted Q.size in the structure type. It is empty when Q.size=0 and full when Q.size=MaxSize.

3. Add a flag tag in the structure type to distinguish whether the team is full or empty. When tag is equal to 0, if Q.front=Q.rear due to deletion, it is empty; When tag is equal to 1, if Q.front=Q.rear due to insertion, the team is full.

Common operation

#include <stdio.h>
#include <stdlib.h>

#define MaxSize 50
typedef struct {
	int data[MaxSize];
	int front;
	int rear;
} SqQueue;

//Initialize queue
void initQueue(SqQueue *s) {
	s->front = s->rear = 0;
}

//Determine whether the queue is empty
bool isQueueEmpty(SqQueue *s) {
	if ((s->rear + MaxSize - s->front) % MaxSize == 0) {
		printf("Queue empty!!!\n");
		return true;
	}
	printf("The queue is not empty!!!\n");
	return false;
}

//Join the team
bool enQueue(SqQueue *s, int e) {
	if ((s->rear + 1) % MaxSize == s->front) {
		return false; //If the team is full, it will fail to join the team
	}
	s->data[s->rear] = e;
	s->rear = (s->rear + 1) % MaxSize;
	printf("%d Team success\n", e);
	return true;
}

//Out of the team
bool deQueue(SqQueue *s, int *e) {
	if (s->rear == s->front) {
		return false; //If the team is empty, the team fails
	}
	*e = s->data[s->front];
	s->front = (s->front + 1) % MaxSize;
	printf("%d Team success\n", *e);
	return true;
}

//Queue empty
void emptyQueue(SqQueue *s) {
	s->front = s->rear = 0;
}

//Queue destruction
void destroyQueue(SqQueue *s) {
	free(s->data);
	free(s);
}

int main() {
	SqQueue s;
	initQueue(&s);
	isQueueEmpty(&s);
	int a = 10;
	int b = 13;
	int c = 15;
	int d;
	enQueue(&s, a);
	enQueue(&s, b);
	enQueue(&s, c);
	deQueue(&s, &d);
	deQueue(&s, &d);
	emptyQueue(&s);
	destroyQueue(&s);
	return 0;
}

Chain queue

structure type

typedef struct LinkNode {
	int data;
	LinkNode *next;
} LinkNode;
typedef struct {
	LinkNode *front, *rear;
} LinkQueue;

Common operation

#include <stdio.h>
#include <stdlib.h>

typedef struct LinkNode {
	int data;
	LinkNode *next;
} LinkNode;
typedef struct {
	LinkNode *front, *rear;
} LinkQueue;

//Initialize queue
void initQueue(LinkQueue *Q) {
	Q->front = Q->rear = (LinkNode *)malloc(sizeof(LinkNode));
	Q->front->next = NULL;
}

//Determine whether the queue is empty
bool isQueueEmpty(LinkQueue *Q) {
	if (Q->rear == Q->front) {
		printf("Queue empty!!!\n");
		return true;
	}
	printf("The queue is not empty!!!\n");
	return false;
}

//Join the team
bool enQueue(LinkQueue *Q, int e) {
	LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));
	s->data = e;
	s->next = NULL;
	Q->rear->next = s;
	Q->rear = s;
	printf("%d Team success\n", e);
	return true;
}

//Out of the team
bool deQueue(LinkQueue *Q, int *e) {
	if (Q->front == Q->rear) {
		return false; //If the team is empty, the team fails
	}
	LinkNode *s = Q->front->next;
	*e = s->data;
	Q->front->next = s->next;
	if (s == Q->rear) {
		Q->rear = Q->front; //If there is only one element left in the original queue, you need to change the position of the rear pointer
	}
	free(s);
	printf("%d Team success\n", *e);
	return true;
}

//Queue empty
void emptyQueue(LinkQueue *Q) {
	if (Q->front == Q->rear) {
		return;
	}
	LinkNode *p = Q->front->next;
	LinkNode *temp;
	while (p != Q->rear) {
		temp = p;
		p = p->next;
		free(temp);
	}
	free(p);
	Q->rear = Q->front;
}

//Queue destruction
void destroyQueue(LinkQueue *Q) {
	free(Q);
}

int main() {
	LinkQueue s;
	initQueue(&s);
	isQueueEmpty(&s);
	int a = 10;
	int b = 13;
	int c = 15;
	int d;
	enQueue(&s, a);
	enQueue(&s, b);
	enQueue(&s, c);
	deQueue(&s, &d);
	emptyQueue(&s);
	destroyQueue(&s);
	return 0;
}

Double ended queue

Double ended queue refers to a queue that allows both ends to enter and leave the queue. The logical structure of its elements is still linear. The two ends of the queue are called the front end and the back end respectively, and both ends can join and leave the queue.

Output restricted double ended queue: a double ended queue that allows insertion and deletion at one end but only insertion at the other end is called output restricted double ended queue.

Double ended queue with restricted input: a double ended queue that allows insertion and deletion at one end but only deletion at the other end is called a double ended queue with restricted input.

If the elements inserted from an endpoint of a dual ended queue can only be deleted from that endpoint, the dual ended queue will degenerate into two stacks adjacent to the bottom of the stack.

Application of stack and queue

Application of stack: bracket matching, expression evaluation (conversion between infix expression and pre suffix expression), recursion (Hanoi Tower and Fibonacci sequence), traversal of tree in order, in order and then in order, etc.

Application of queue: hierarchical traversal of binary tree, waiting queue of computer system, etc.

parenthesis matching

It mainly refers to whether the matching {}, [], () are paired.

Expression evaluation

There are three formulas: infix expression Prefix expression (polish), suffix expression (inverse Polish), in which infix expression is a normal expression friendly to human beings. Infix expression is friendly to machine storage and operation, so the mutual conversion of infix expression and pre suffix expression will be involved when the program is compiled or interpreted as machine instructions. The method is to move the operation symbols before or after the operands after determining the operation priority.

35,15,+,80,70,-,*,20,/                      //Suffix expression
(((35+15)*(80-70))/20)=25                 //Infix expression  
/,*,+,35,15,-,80,70, 20                   //Prefix expression

Recursion - Tower of Hanoi

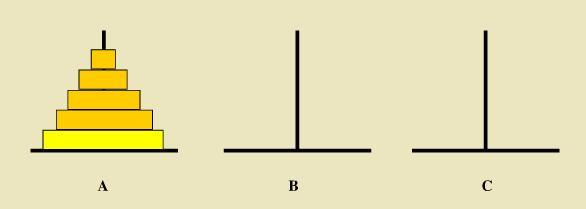
#include <stdio.h>
void HanNuo(int n, char a, char b, char c) {
	if (n == 1) { //This is also the termination condition of recursion
		printf("Put the plate%d from %c -----> %c\n", n, a, c); //The console outputs the trend of each operation
	} else {
		HanNuo(n - 1, a, c, b);      //Move n-1 plates from top to bottom on column a to column b
		printf("Put the plate%d from %c -----> %c\n", n, a, c);
		HanNuo(n - 1, b, a, c);      //Move n-1 plates on column b to column c
	}
}
int main() {
	HanNuo(10,'a','b','c');
	return 0;
}

Recursive Fibonacci sequence

This sequence starts with Item 3, and each item is equal to the sum of the first two items.

#include <stdio.h>
int main()
{
    long i, n, t1 = 0, t2 = 1, nextTerm;
    printf("Output several items(n>0): ");
    scanf("%d", &n);
    printf("Fibonacci sequence: ");
    for (i = 1; i <= n; ++i)
    {
        printf("%d, ", t1);
        nextTerm = t1 + t2;
        t1 = t2;
        t2 = nextTerm;
    }
    return 0;
}