Linear Table
1. Definition of Linear Table
A linear table is a finite sequence of n(n < 0) data elements of the same data type, where n is the table length, and a linear table is an empty table when n=0. If a linear table is named L, it is generally expressed as L = ( a 1 , a 2 , . . . , a i , . . . , a n ) L=(a_1,a_2, ... ,a_i, ... ,a_n) L=(a1,a2,...,ai,...,an)
Explanation:
- a i a_i ai is the bit order in the linear table of the "ith" element in the linear table
- a 1 a_1 a1 is a header element; a n a_n an is the tail element
- With the exception of the first element, each element has and only has a direct precursor; Except for the last element, each element has and only has a direct successor
[External chain picture transfer failed, source station may have anti-theft chain mechanism, it is recommended to save the picture and upload it directly (img-TNeXFSAd-16420019324) (C:Userszc2610DesktopData Structureimgimage-20207089.png)]
2. Basic operations of linear tables
- InitList (&L): Initializes the table. Construct an empty linear table L to allocate memory space
- DestroyList (&L): Destroy operation. Destroy the linear table and free up memory space occupied by the linear table L
- ListInsert (&L, i, e): Insert operation. Inserts the specified element E at the ith position in Table L
- ListDelete (&L, i, &e): Delete operation. Delete the element at position I I in table L and return the value of the deleted element with E.
- LocateElem(L,e): Find operations by value. Find elements in Table L that have a specific given key value.
- GetElem(L,i): Bit-by-bit lookup operation. Gets the value of the element at position I I in table L.
- Length(L): Find the table length. Returns the length of the linear table L, the number of data elements in L
- PrintList(L): Output operation. Output all element values of the linear table L in order of front and back.
- Empty(L): Null operation. Returns true if L is an empty table, otherwise returns flase.
Tips:
- Operation on Data (Memory Thought) - Create Sales, Add, Delete, Change Check
- C language function definition - <return value type>function name (<parameter 1 type>parameter 1, <parameter 2 type>parameter 2,...)
- In actual development, other basic operations can be defined based on actual needs
- The form and naming of function names and parameters can be changed (Reference here: Yan Weimin's Data Structure)
- When to pass in a reference to a parameter,'&'- The result of modifying the parameter needs to be brought back.
'&'denotes a reference call in the C++ language, and the same effect can be achieved by using pointers in the C language.
3. Sequential representation of linear tables
Note:
- ElemType represents an element type, which can be int, char, float, double, and so on, or a structure.
- The following code is C++ based pseudocode and cannot run independently.
- The pseudocode for some of the specific operations below does not represent the only writing, but the basic idea is the same.
3.1. Definition of Sequential Table
Sequential Table - A linear table is implemented using sequential storage.
Sequential storage: Store logically adjacent elements in storage units that are also adjacent to each other in physical locations. The relationship between elements is achieved by the adjacency relationship of storage units.
3.2. Implementation of Sequential Table
- The most important feature of a sequence table is random access, where the specified elements can be found within time O(1) by the first address and the element number.
- Sequential tables have a high storage density, with each node storing only data elements.
- Logically adjacent elements of a sequence table are physically adjacent, so insertion and deletion operations require a large number of elements to be moved.
3.2.1, Static Allocation
#define MaxSize 10 // Define maximum length
typedef struct{
ElemType data[MaxSize]; //Store data elements in a static "array"
int length; //Current length of sequential table
}SeqList; //Type Definition of Sequential Table
When allocated statically, because the size and spatial implementation of the array are fixed, once the space is full, adding new data will overflow, causing the program to crash.
3.2.2, Dynamic Allocation
#define InitSize 10 // Default maximum length
typedef struct{
ElemType *data; //Pointer indicating dynamic allocation of array
int MaxSize; //Maximum capacity of sequential tables
int length; //Current length of sequential table
}SeqList; //Type Definition of Sequential Table
key: dynamically request and free memory space
1. C-malloc, free functions
//malloc call format (type specifier*)malloc(size)
Function: Allocate a contiguous area of "size" bytes in the dynamic storage of memory. The return value of the function is the first address of the area.
-
The Type Specifier indicates what data type the area is used for.
-
(Type specifier*) means to cast the return value to the type pointer.
-
"size" is an unsigned number.
//free Call Format free(void*ptr);
Function: Release a block of memory space that ptr points to. ptr is a pointer variable of any type that points to the first address of the area being released. Released areas should be areas allocated by malloc or calloc functions.
The header file for malloc, free functions is #include <stdlib. H>
2. C++ - new, delete keywords
//new Call Format Format 1: Pointer variable name=new Type Identifier; For example: int *a=new int; //Opens up a storage space for integers and returns an address pointing to that storage space. Format 2: Pointer variable name=new Type identifier (initial value); For example: int *a=new int(a); //Opens up a storage space for integers, returns an address to the storage space, but assigns the integer space a value of 5. Format 3: Pointer variable name=new Type Identifier [Number of memory units]; For example: int *a = new int[100]; //Open up an integer array space of size 100
The data type must be known when using the new operator, which will request sufficient storage space from the system heap, return the first address of the memory block if the request is successful, or return a zero value if the request is unsuccessful.
//delete call format delete Pointer variable name; For example: int *a = new int;delete a; //Release the space of the int pointer
delete Delete address space
Dynamic allocation of specific implementation code
#define InitSize 10 // Default maximum length
typedef struct{
int *data; //Pointer indicating dynamic allocation of array
int MaxSize; //Maximum capacity of sequential tables
int length; //Current length of sequential table
}SeqList; //Type Definition of Sequential Table
//Initializing a dynamic allocation sequence table
void InitList(SeqList &L){
//Request a contiguous block of storage with the malloc function
L.data=(int *)malloc(InitSize*sizeof(int));
L.length=0;
L.MaxSize=InitSize;
}
//Increase the size of dynamic space
void IncreaseSize(SeqList &L,int len){
int *p=L.data;
L.data=(int *)malloc((L.MaxSize+len)*sizeof(int));
for(int i=0;i<L.length;i++){
L.data[i]=p[i]; //Copy data to a new area
}
L.MaxSize=L.MaxSize+len; //Sequence table maximum length increase len
free(p); //Release the original memory space
}
int main(){
SeqList L; //Declare a Sequential Table
InitList(L); //Initialization Sequence Table
//.... Omit some code here and insert a few elements
IncreaseSize(L,5);
return 0;
}
3.3. Implementation of Basic Operations on Sequence Table
(1) Insert operation

#define MaxSize 10 // Define maximum length
typedef struct{
ElemType data[MaxSize]; //Store data elements in a static "array"
int length; //Current length of sequential table
}SqList; //Type Definition of Sequential Table
//----------------------- Insert operation core code-----------------------
void ListInsert(SqList &L,int i,ElemType e){
for(int j=L.length;j>=i;j--){//Move the f i rst and subsequent elements back
L.data[j]=L.data[j-1];
}
L.data[i-1]=e; //Place e at position i
L.length++; //Length plus 1
}
//----------------------- Insert operation core code-----------------------
int main(){
SqList L; //Declare a Sequential Table
InitList(L); //Initialization Sequence Table
//.... Omit some code here and insert a few elements
ListInsert(L,3,3);
return 0;
}
For example: ListInsert(L,9,3); The location of the insert is illegal and the code is not robust. Modify the code.
bool ListInsert(SqList &L,int i,ElemType e){
if(i<1||L.length+1) //Determine if the range of i is valid
return false;
if(L.length>=MaxSize) //Current storage is full and cannot be inserted
return false;
for(int j=L.length;j>=i;j--){//Move the f i rst and subsequent elements back
L.data[j]=L.data[j-1];
}
L.data[i-1]=e; //Place e at position i
L.length++; //Length plus 1
return ture;
}
(2) Delete operation
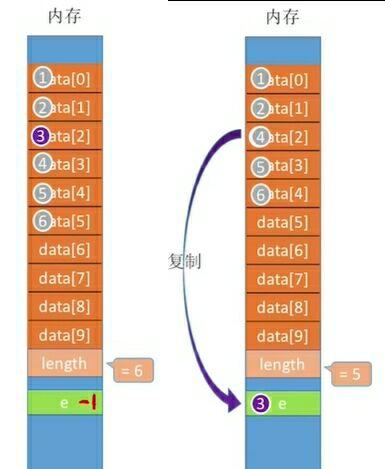
//------------------------- Delete operation core code---------------------
bool ListDelete(SeqList &L,int i,ElemType &e){
if(i<1||i>L.length) //Determine if the range of i is valid
return false;
e=L.data[i-1];
for(int j=i;j<L.length;j++){
L.data[j-1]=L.data[j];
}
L.length--;
return true;
}
//------------------------- Delete operation core code---------------------
int main(){
SeqList L; //Declare a Sequential Table
InitList(L); //Initialization Sequence Table
//... Omit some code here and insert a few elements
int e=-1; //Bring the deleted element back with variable e
if(ListDelete(L,3,e))
printf("Successfully deleted%d",e);
else
printf("Illegal bit order, deletion failed");
return 0;
}
(3) Search operation
-
Bitwise Search
//Return the elements found ElemType GetElem(SeqList L,int i){ return L.data[i-1]; } -
Find by value
//Returns the order in which elements were found int LocateElem(SeqList L,ElemType e){ for(int i=0;i<L.length;i++){ if(L.data[i]==e) return i+1; } return 0; }
3.3. Code implementation of sequence table
Implementation code for basic operation of sequential table
4. Chain Representation of Linear Tables
4.1, Single-Chain List
4.1.1, Definition of single-chain list
Chained storage of a linear table, also known as a single-chain table, refers to the storage of data elements in a linear table through an arbitrary set of storage units. In order to establish a linear relationship between data elements, for each chain table node, in addition to storing the information of the element itself, a pointer to its successors is needed
Specific description of node types in single-chain list
typedef struct LNode{ //Define single-chain list node type
ElemType data; //Data Domain
struct LNode *next; //Pointer field
}LNode,*LinkList;
typedef Keyword - data type rename
//Usage of typedef: typedef <data type> <alias>
struct LNode{
ElemType data;
struct LNode *next;
};
typedef struct LNode LNode; //Rename struct LNode to LNode
typedef struct LNode *LinkList; //Rename struct LNode* to LinkList
//-----------------------------------------
typedef struct LNode{ //Define single-chain list node type
ElemType data; //Data Domain
struct LNode *next; //Pointer field
}LNode,*LinkList;
//-----------------------------------------
Be careful:
Use LinkList to emphasize that this is a single-chain list
Use LNode * to emphasize that this is a node
4.1.2, Head Pointer and Head Node
Definition
Head pointer: A pointer to the first node of a linked list, usually a single linked list, represented by a header pointer.
Head node: For operational convenience, a node can be added or not before the first node in the single-chain list.
Difference
The head pointer always points to the first node of the chain table, regardless of whether it has a head node or not. A head node is the first node in the chain table with a head node, and information is usually not stored in the node.
Head Node Advantages
Since the position of the first data node is stored in the pointer field of the head node, the operation at the first position of the chain table is consistent with that at other locations in the table, and no special treatment is required.
(2) Whether the chain table is empty or not, its head pointer points to the non-null pointer of the head node (the pointer field of the head node in an empty table is empty), so the processing of the null and non-null tables is unified.
Single-chain list without header nodes
typedef struct LNode{ //Define single-chain list node type
ElemType data; //Each node holds a data element
struct LNode *next; //Pointer to Next Node
}LNode,*LinkList;
//Initialize an empty single-chain list
bool InitList(LinkList &L){
L=NULL; //Empty table, no nodes yet. Prevent dirty data
return true;
}
int main(){
LinkList L; //Declare a pointer to a single-linked list
//Initialize an empty table
InitList(L);
}
Single Chain List with Head Nodes
typedef struct LNode{ //Define single-chain list node type
ElemType data; //Each node holds a data element
struct LNode *next; //Pointer to Next Node
}LNode,*LinkList;
//Initialize an empty single-chain list
bool InitList(LinkList &L){
L=(LNode *)malloc(sizeof(LNode));//Assign a header node
if(L==NULL) //Insufficient memory, allocation failed
return false;
L->next=NULL; //There are no nodes yet after the head node
return ture;
}
int main(){
LinkList L; //Declare a pointer to a single-linked list
//Initialize an empty table
InitList(L);
}
Description: The difference between a header node and a non-header node is that a header node needs to be allocated first when initializing.
4.1.3. Implementation of Basic Operations on Single Chain Lists
1. Insert operation
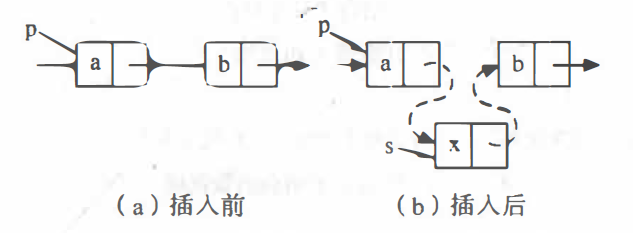
1. Bitwise insertion (leading node)
//Insert element E (leading node) at position i I
bool ListInsert(LinkList &L,int i,ElemType e){
LNode *p; //Pointer p points to the currently scanned node
int j=0; //The last node to which the current p points
p=L; //L points to the head node, which is the 0th node (there is no data)
while(p&&j<i-1){ //Loop to find node i-1
p=p-> next;
j++;
}
if(!p||j>i-1) //Illegal I value (i>n+1 or i<1)
return false;
LNode *s=(LNode *)malloc(sizeof(LNode));//Generating new nodes*s
s-data=e; //Set the data field of node*s to e
s->next=p->next; //Statement One
p->next=s; //Statement Two
return ture; //Insert Successful
}
Be careful:
The order of statements 1 and 2 cannot be changed. If p->next=s is executed before s->next=p->next, s->next will be issued pointing to the node itself.
2. Bitwise insertion (no header node)
//Insert element E (no header node) at the first position
bool ListInsert(LinkList &L,int i,ElemType e){
if(i==1){
LNode *s=(LNode *)malloc(sizeof(LNode));
s->data=e;
s->next=L;
L=s; //Head Pointer Points to New Node
return ture;
}
LNode *p; //Pointer p points to the currently scanned node
int j=1; //The last node to which the current p points
p=L; //p points to the first node (note: not the header node)
while(p&&j<i-1){ //Loop to find node i-1
p=p-next;
j++;
}
if(!p||j>i-1) //Illegal I value (i>n+1 or i<1)
return false;
LNode *s=(LNode *)malloc(sizeof(LNode));//Generating new nodes*s
s-data=e; //Set the data field of node*s to e
s->next=p->next;
p->next=s;
return ture;
}
Description: If you do not have a header node, you need to modify the header pointer L when inserting or deleting the first element.
3. Postpolation of specified nodes
//Post-insert operation: insert element e after p-node
bool InsertNextNode(LNode *p,ElemType e){
if(p==NUll)
return false;
LNode *s=(LNode *)malloc(sizeof(LNode));//Generating new nodes*s
if(s==NUll) //memory allocation failed
return false;
s->data=e; //Set the data field of node*s to e
s->next=p->next;
p->next=s;
return ture; //Insert Successful
}
4. Pre-interpolation of specified nodes
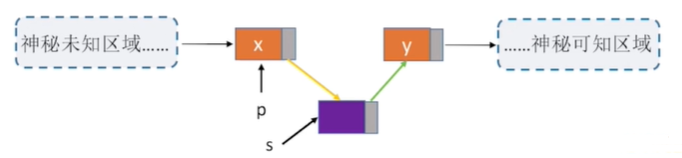
//Pre-insert operation: insert element e before p-node
bool InsertNextNode(LNode *p,ElemType e){
if(p==NUll)
return false;
LNode *s=(LNode *)malloc(sizeof(LNode));//Generating new nodes*s
if(s==NUll) //memory allocation failed
return false;
s->next=p->next;
p->next=s; //New node s after p
s->data=p->data; //Copy elements from p into s
p->data=e; //Elements in p are covered by e
return ture; //Insert Successful
}
Interpretation: Because no node before the p-node can be found, a new s-node can only be inserted after the p-node. The data of the two nodes is then exchanged, in a disguised form equivalent to before the insertion into the p-node.
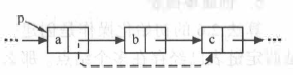
2. Delete Operation
1. Delete in bitwise order (leading node)
bool ListDelete(LinkList &L,int i,ElemType &e){
LNode *p;
int j=0;
p=L;
while((p->next)&&(j<i-1)){//Find the i-1 node to which p points
p=p->next;
j++;
}
if(!(p->next)||(j>i-1))//The deletion position is unreasonable when i>n or i<1
return false;
LNode *q=p->next; //Temporarily save deleted addresses for release
e=q->data;
p->next=q->next; //Changing the pointer field for deleting precursor nodes of a node
free(q) //Release storage space for nodes
}
Explain
There is a difference between deleting the cyclic condition** (p->next&j<i-1) in the algorithm and inserting the cyclic condition (p&j<i-1)** in the algorithm. Because there are n+1 legal insertion positions in the insert operation and only n legal deletion positions in the delete operation, if the same circular condition as the insert operation is used, the null pointer will be referenced and the delete operation will fail.
2. Deletion of specified nodes
bool DeleteNode(LNode *p){
if(p==NUll)
return false;
LNode *q=p->next; //Point q to the next node of *p
p->data=p->next->data; //Exchange data fields with subsequent nodes
p->next=q->next; //Break *q Node from Chain
free(q); //Release storage space for subsequent nodes
return ture;
}
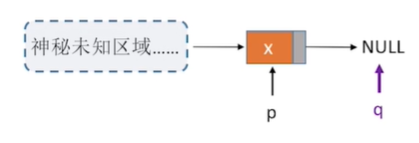
If it is the last node of p, only the precursor of p, time complexity O(n), can be found in turn from the header
3. Find Operation
It's all about leading nodes

1. Bitwise Search
//Bitwise lookup returns the first element (leading node)
LNode * GetElem(LinkList L,int i){
if(i<0)
return NULL;
LNode *p; //Pointer p points to the currently scanned node
int j=0; //The current p is pointing to the number of nodes
p=L; //L points to the head node, which is the 0th node (there is no data)
while(p!=NULL&&j<i){ //Loop to find the ith node
p=p->next;
j++;
}
return p;
}
2. Find by Value
//Look by value to find a node (leading node) with data field==e
LNode *LocateElem(LinkList L,ElemType e){
LNode *p=L->next;
//Find nodes with data e starting from the first node
while(p&&p->data!=e)
p=p->next;
return p; //Return a pointer to the node when found, otherwise return NULL
}
4. Establishment of Single Chain List
1. Tail Interpolation
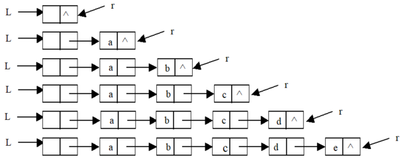
void CReateLIst_R(LinkList &L,int n){
//Enter the values of n elements in positive order to create a single-chain table L with header nodes
L=(LinkList)malloc(sizeof(LNode));
L->next=NULL; //Establish an empty list of leading nodes first
LNode *p;
LNode *r=L; //Tail pointer r to head node
for(i=0;i<n;i++){
p=(LinkList)malloc(sizeof(LNode));//Generate new nodes
cin>>p->data; //Data field whose input element values are copied to the new node*p
p->next=NULL; //The newly inserted node pointer is empty
r->next=p; //After inserting the new node *p into the endpoint *r
r=p; //r points to the new endpoint*p
}
}
2. Head Interpolation
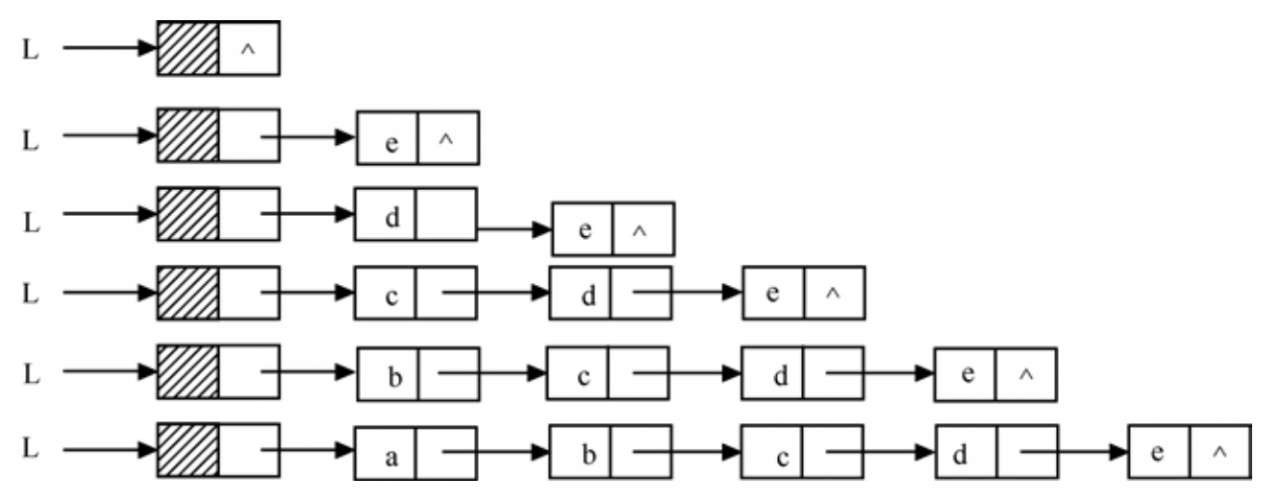
void CreateList_H(LinkList &L,int n){
//Enter the values of n elements in reverse order to create a single-chain table L with header nodes
L=(LinkList)malloc(sizeof(LNode));
L->next=NULL; //Establish an empty list of leading nodes first
LNode *p;
for(int i=0;i<n;i++){
p=(LinkList)malloc(sizeof(LNode));//Generate new nodes*p
cin>>p->data; //Data field whose input element values are copied to the new node*p
p->next=L->next;L->next=p; //Insert new node *p after the head node
}
}
4.1.4, Code implementation of single-chain list
Implementation code for basic operation of single-chain list
4.2, Double Chain List
4.2.1, Definition of Double Chain Table
In single-chain tables, the execution time for finding direct successor nodes is O(1), while the execution time for finding direct precursors is O(n). To overcome the unidirectionality of single-linked lists, a two-way linked list can be used.
As the name implies, there are two pointer domains in a two-way chain table node, one pointing to direct succession and the other pointing to direct precursor. The node structure is illustrated below.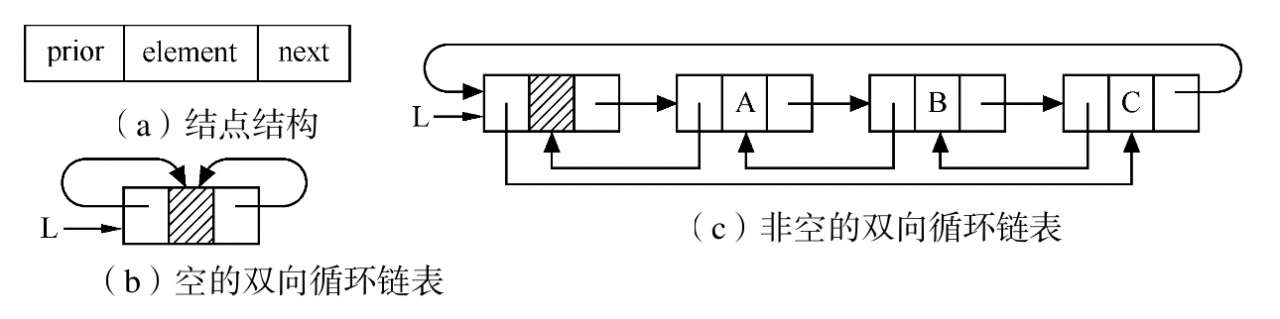
//--Storage structure in two-way linked list
typedef struct DuLNode{
ElemType data; //Data Domain
struct DuLNode *prior; //Point to Direct Forward
struct DuLNode *next; //Point to Direct Back-Drive
}DuLNode,*DuLinkList;
4.2.2. Implementation of Basic Operations on Double Chain Lists
1. Initialization of Double Chain List
bool InitDLinkList(DLinkList &L){
L=(DuLNode *)malloc(sizeof(DuLNode)); //Assign a header node
if(L==NULL) //Insufficient memory, allocation failed
return false;
L->prior=NULL; //Head node prior always points to NULL
L->next=NULL; //There are no nodes yet after the head node
return true;
}
2. Insertion of Two-way Chain List
(1) Insert before p node
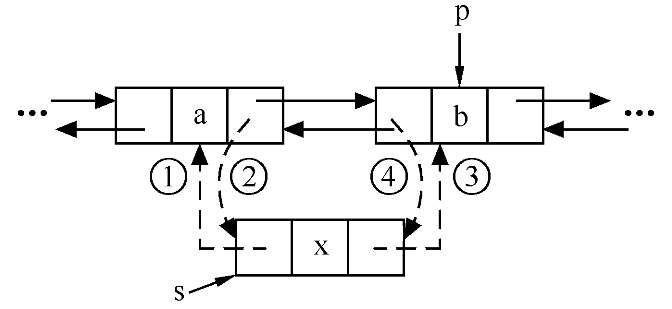
bool ListInsert_DuL(DuLinkList &L,int i,ElemType e){
//Insert element e before position i I in double-chain list L with leading node
DuLNode *p,*s;
if(!(p=GetElem_DuL(L,i))) //Determines the position pointer p of the ith element in L
return false; //The first element does not exist when p is NULL
s=(DuLNode *)malloc(sizeof(DuLNode));//Generating new nodes*s
s->data=e; //Set node*s data field to e
s->prior=p->prior; //Insert node *s into L, this step corresponds to Figure 1 above
p->prior->next=s; //Corresponds to Figure 2 above
s->next=p; //Corresponds to Figure 3 above
p->prior=s; //Corresponds to Figure Four above
return true;
}
Note the order before and after.
(2) Insert after p node
//Insert s node after p node
bool InsertNextDuLNode(DuLNode *p,DuLNode *s){
if(p==NULL||s==NULL) //illegal parameter
return false;
s->next=p->next;
if(p->next!=NULL) //If the p-node has a successor node
p->next->prior=s;
s->prior=p;
p->next=s;
return true;
}
Note: The main difference between insertion before and after a p-node is that when inserting after a p-node, it is necessary to determine whether the p-node is the last node.
Summary: It's hard to understand who is pointing to whom the insertion operation pointer is, and of course, it's impossible to remember the order. Here's a little trick (as shown by the insertion before the p-node):
(1) Find the pointer field farthest from node P, that is, the front of S node. So there are operations: (1) and (2) without sequence
(2) Because the S node is inserted, it needs to be initiated actively. So first is 1, then is 2
(3) Look at the pointer field on the other side, that is, the back-drive of S node.
(4) Because the S node is inserted, it needs to be initiated actively. So there are three first, then four
3. Deletion of Two-way Chain List
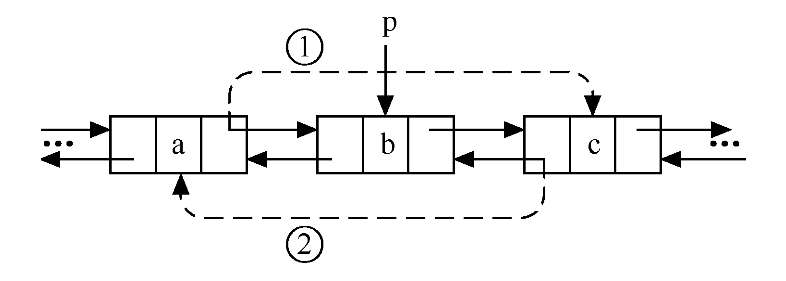
void ListDelete_DuL(DuLinkList &L,int i){
//Delete the ith element from the two-way chain list L with the leading node
DuLNode *p,*s;
if(!(p=GetElem_DuL(L,i))) //Determines the position pointer p of the ith element in L
return false; //The first element does not exist when p is NULL
p->prior->next=p->next; //Modify the successor pointer of the precursor node of the deleted node, corresponding to Figure 1 above
p->next->prior=p->prior; //Modify the precursor pointer of the succeeding node of the deleted node, corresponding to Figure 2 above
free(p); //Release space for deleted nodes
}
Deleting the succeeding nodes of a p-node
//Deleting the succeeding nodes of a p-node
bool DeleteNextDuLNode(DuLNode *p){
if(p==NULL)
return false;
DuLNode *q=p->next; //Find the succeeding node q of p
if(q==NULL) //p has no successors
return false;
p->next=q->next;
if(q->next!=NULL) //q node is not the last node
q->next->prior=p;
free(q); //Release Node Space
return true;
}
4.3, Circular Chain List
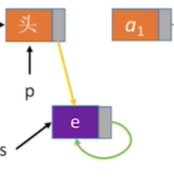
4.3.1, Circular Single Chain List

Circular Single Chain List: Any other node can be found from one node
//Initialize a circular single-chain list
bool InitList(LinkList &L){
L=(LNode *)malloc(sizeof(LNode));//Assign a header node
if(L==NUll) //Insufficient memory allocation failed
return false;
L->next=L; //Head Node next Points to Head Node
return true;
}
4.3.2, Circular Double Chain List
//Circular Double Chain List Initialization
bool InitDuLinkList(DuLinkList &L){
L=(DuLNode *)malloc(sizeof(DuLNode));//Assign a header node
if(L==NULL) //Insufficient memory, allocation failed
return false;
L->prior=L; //The prior of the head node points to the head node
L->next=L; //next of Head Node Points to Head Node
return true;
}
Insertion of Double Chain List
//Insert s node after p node
bool InsertNextDuLNode(DuLNode *p,DuLNode *s){
s->next=p->next;
p->next->prior=s;
s->prior=p;
p->next=s;
return true;
}
It is not necessary to judge whether a p-node is the last node as a one-way double-chain table.
Deletion of Double Chain List
//Deleting the succeeding nodes of a p-node
bool DeleteNextDuLNode(DuLNode *p){
if(p==NULL)
return false;
DuLNode *q=p->next; //Find the succeeding node q of p
p->next=q->next;
q->next->prior=p;
free(q); //Release Node Space
return true;
}
It is not necessary to determine whether P has a successor or whether p's successor node is the last node, like a one-way double-chain table
4.4, Static Chain List
Static Chain List: Allocate a whole contiguous block of memory space for each node to be placed centrally.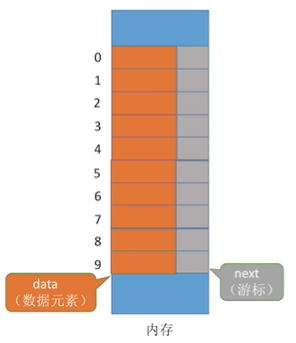
Definition of Static Chain List
#define MaxSize 10 // Maximum Length of Static Chain List
struct Node{ //Definition of static list structure type
ElemType data; //Store data elements
int next; //Array subscript for next element
};
void testSLinkList(){
struct Node a[MaxSize];
//Array a as static chain table
}
//Another Equivalent Writing Method
struct Node{ //Definition of static list structure type
ElemType data; //Store data elements
int next; //Array subscript for next element
}SLinkList[MaxSize];
void testSLinkList(){
SLinkList a ;
//Array a as static chain table
}
Summary:
Static list: A list of chains implemented as an array.
Advantages: Additions and deletions do not require a large number of moving elements.
Disadvantages: It cannot be accessed randomly, it can only be searched from the beginning to the end. Capacity is fixed.
Fit to the scene: 1. Low-level languages that do not support pointers. (2) Scenes with a fixed number of data elements.
4.5, Comparison of Sequence Table and Chain Table
4.5.1. Comparison of Spatial Performance
(1) Allocation of storage space
Sequential table: Storage space must be pre-allocated, and the number of elements is limited to some extent, which can lead to waste of storage space or space overflow.
Chain list: There is no need to pre-allocate space for it. As long as memory allows, there is no limit to the number of elements in the list.
(2) Storage density
Insert a picture description here
Sequential tables have a storage density of 1, while chain tables have a storage density of less than 1. If each element data domain takes up less space, the pointer's structural overhead takes up most of the space of the entire node, resulting in a smaller storage density.
4.5.2, Time Performance Comparison
(1) Efficiency of accessing elements
Sequential tables are implemented by arrays and are a random access structure. By specifying the ordinal number i of any location, elements at that location can be accessed directly within O(1) time, which means the efficiency of value retrieval is high.
A chain table is a sequential access structure. When accessing the first element i n a chain table by location, the chain table can only be traversed backwards from the header until the element at the second location is found. The time complexity is O(n), which means the efficiency of the value-taking operation is low.
(2) Efficiency of insert and delete operations
Once the location of insertion or deletion is determined, the insertion or deletion operation does not need to move the data, only the pointer needs to be modified, and the time complexity is O(1).
When inserting or deleting a sequential table, on average, nearly half of the nodes in the table are moved with O(n) time complexity. Especially when each node has a large amount of information, the time cost to move the node is considerable.