Definitions and basic terms of drawings

 
Figure: G=(V, E)    Grapg = (Vertex, Edge)
   V: finite non empty set of vertices (data elements);
  E: finite set of edges

Undirected graph: each edge is undirected
Directed graph: each edge has a direction

Complete graph: any two points have an edge connected

Sparse graph: a graph with few edges or arcs (e < nlogn)
Dense graph: a graph with many edges or arcs
Net:   edge / arc weighted graph
Adjacency:   the relationship between two vertices connected by edges / arcs
      exists (vi, vj), then vi and vj are called adjacent points to each other;
     if there is < vi, vj >, it is said that vi is adjacent to vj, and vj is adjacent to vi
Association (attachment): relationship between edge / arc and vertex
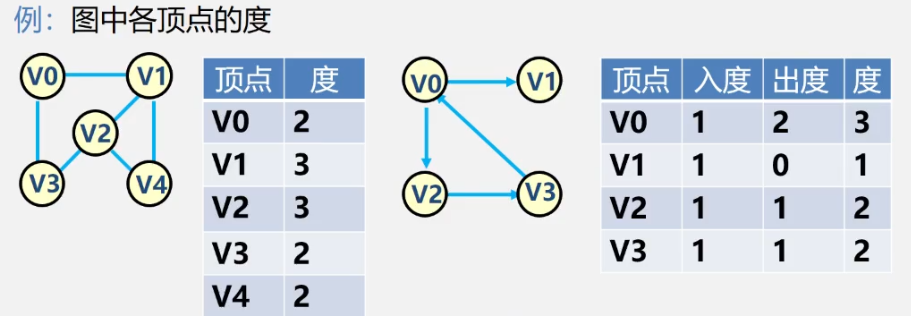
Degree of vertex: the number of edges associated with the vertex, recorded as TD(v)
In a directed graph, the degree of a vertex is equal to the sum of the in and out degrees of the vertex
The penetration of vertex v is the number of directed edges focusing on V, which is recorded as ID(v)
The outgoing degree of vertex v is the number of directed edges with V as the starting point, which is recorded as OD(v)

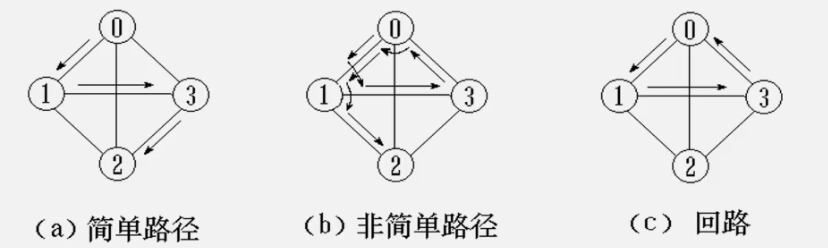
Path: a sequence of vertices formed by successive edges
Path length: the sum of the number / weight of edges or arcs on the path
Loop (loop): the first vertex and the last vertex are the same path
Simple path: a path with different vertices except for the same starting point and ending point of the path

Connected graph (strongly connected graph)
   in the directed graph G = (v, {E}), if there is a path from v to u for any two vertices v and u, then G is a connected graph (strongly connected graph)

Rights and networks:
   the correlation number of edges or arcs in a graph is called weight, which indicates the distance or cost from one vertex to another; A weighted graph is called a net

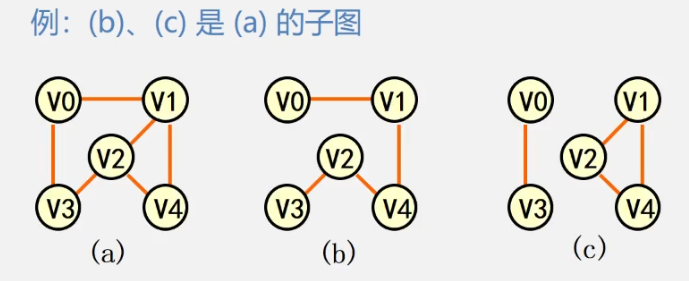
Subgraph:
   let g = (V, {e}) and G1 = (V1, {E1}). If V1 ⊆ V and E1 ⊆ e, G1 is said to be a subgraph of G

Connected component (strong connected component)

• The polar connected subgraph of undirected graph G is called the connected component of G
  Polar Dalian connected subgraph means that the subgraph is a g-connected subgraph. By adding any vertex of G that is not in the subgraph, the subgraph is no longer connected
  

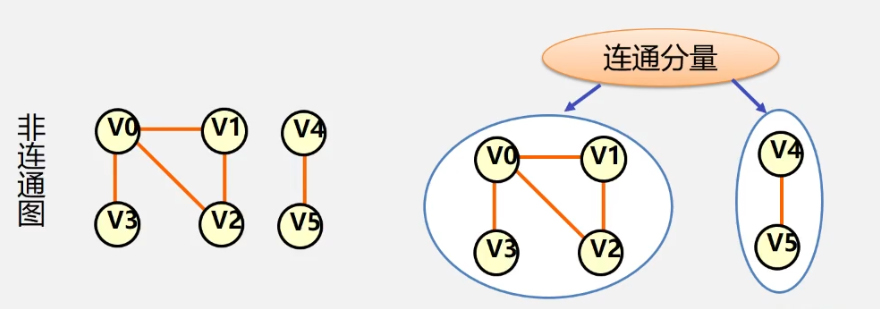
• The maximal strongly connected subgraph of a directed graph G is called the strongly connected component of G
  Maximal strongly connected subgraph means that the subgraph is a strongly connected subgraph of G. by adding any vertex of D that is not in the subgraph, the subgraph is no longer strongly connected
  

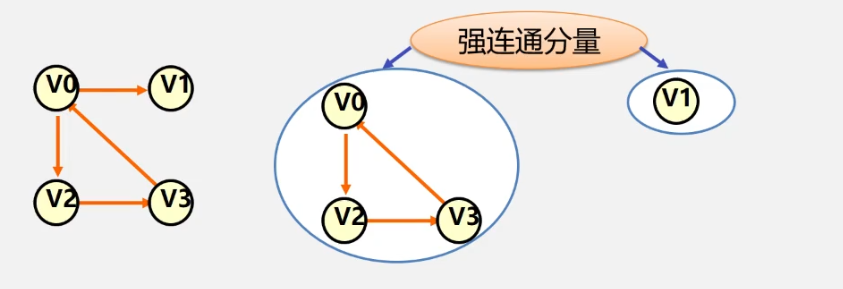
Minimal connected subgraph: the subgraph is a connected subgraph of G. if any edge is deleted from the subgraph, the subgraph is no longer connected
Spanning tree: a minimal connected graph containing all vertices of undirected graph G
Spanning forest: for a non connected graph, a set of spanning trees composed of each connected component

 
 

Type definition of graph

 
The abstract data type of the diagram is defined as follows:

ADT Graph{
   data object V: a collection of data elements with the same characteristics, which is called vertex set
   data relation R: R = {VR}
  VR = {<v,w>|<v,w>| v,w∈V ^ p(v,w)，
    < v, w > represents the arc from v to W, and p(v,w) defines the information of arc < v, w >
  }
  CreateGraph(&G, V, VR)
     initial condition: V is the vertex set of the graph, and VR is the set of arcs in the graph
     operation result: construct diagram G according to the definition of V and VR
  DFSTraverse(G)
     initial condition: figure G exists
     operation result: depth first traversal according to the figure
  BFSTraverse(G)
     initial condition: figure G exists
     operation result: breadth first traversal of the graph
}ADT Graph
 
 

Storage structure of graph

 
Logical structure of graph: many to many
 
 

Array (adjacency matrix representation)

 

• Establish a vertex table (recording the information of each vertex) and an adjacency matrix (representing the relationship between each vertex)
  • Let graph A = (V,E) have n vertices, then
    
  • The adjacency matrix of the graph is a two-dimensional array A.arcs[n][n], which is defined as:

 

Analysis 1: the adjacency matrix of undirected graph is symmetric
Analysis 2: degree of vertex i = number of 1 in row I (column)
In particular: in the adjacency matrix of a complete graph, the diagonal elements are 0 and the rest are 1

 
 

Note: in the adjacency matrix of a directed graph,
   meaning of line I: arc with node vi as tail (i.e. outgoing edge)
   meaning of column I: arc with node vi as the head (i.e. in degree edge)

Analysis 1: the adjacency matrix of a directed graph may be asymmetric
Analysis 2: vertex exit = sum of elements in line i
    penetration of vertex = sum of elements in column i
    degree of vertex = sum of elements in row i + sum of elements in column i
 
 

Adjacency matrix representation of weighted graph

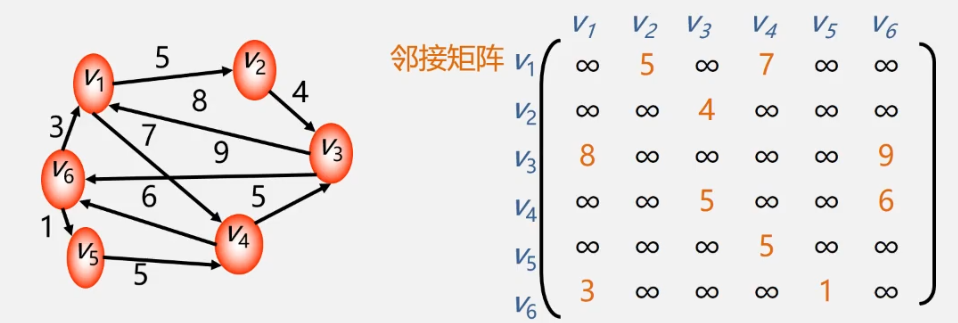
Storage representation of adjacency matrix: two arrays are used to store vertex table and adjacency matrix respectively

#define MaxInt 32767 	// Represents the maximum value, i.e. ∞
#define MVNum 100 		// max vertex 
typedef char VerTexType;	//Set the data type of vertex to character type
typedef int ArcType;	//It is assumed that the weight type of the edge is integer

typedef struct{
	VerTexType vexs[MVNum];		//Vertex table
	ArcType arcs[MVNum][MVNum];		//adjacency matrix 
	int vexnum, arcnum;		//Current number of points and edges of a graph
}AMGraph;	// Adjacency Matrix Graph

 
Using adjacency matrix representation to create undirected network

Algorithm idea:

1. Enter the total number of vertices and edges
2. Input the information of points in turn and store it in the vertex table
3. Initialize the adjacency matrix so that each weight is initialized to a maximum value
4. Construct adjacency matrix

//The adjacency matrix representation is used to create undirected network G
Status CreateUDN(AMGraph &G){
	cin >> G.vexnum >> G.arcnum;	//Enter the total number of vertices and edges
	for(i = 0; i < G.vexnum; ++i)
		cin >> G.vexs[i];			//Enter the information of the points in turn
	for(i = 0; i < G.vexnum; ++i)	//Initialize adjacency matrix
		for(j = 0; j < G.vexnum; ++j)
			G.arcs[i][j] = MaxLnt;		//The weights of the edges are set to the maximum
	
	//Construct adjacency matrix
	for(k = 0; k < G.arcnum; ++k){
		cin >> v1 >> v2 >> w;		//Enter the vertex to which an edge is attached and the weight of the edge
		i = LocateVex(G, v1);
		j = LocateVex(G ,v2);		//Determine the position of v1 and v2 in G
		G.arcs[i][j] = w;			//The weight of edge < V1, V2 > is set to w
		G.arcs[j][i] = G.arcs[i][j];		//Set the weight of the symmetrical edge < V2, V1 > of < V1, V2 > to w
	}
	return OK;
}//CreateUDN

Supplementary algorithm: find vertices in the graph

//Find the vertex u in graph G, and return the subscript in the vertex table if it exists; Otherwise - 1 is returned
int LocateVex(AMGraph G, VertexType u){
	int i;
	for(i = 0; i < G.vexnum; ++i)
		if(u == G.vexs[i])	return i;
	return -1;
}

 
 

 
 

Adjacency table

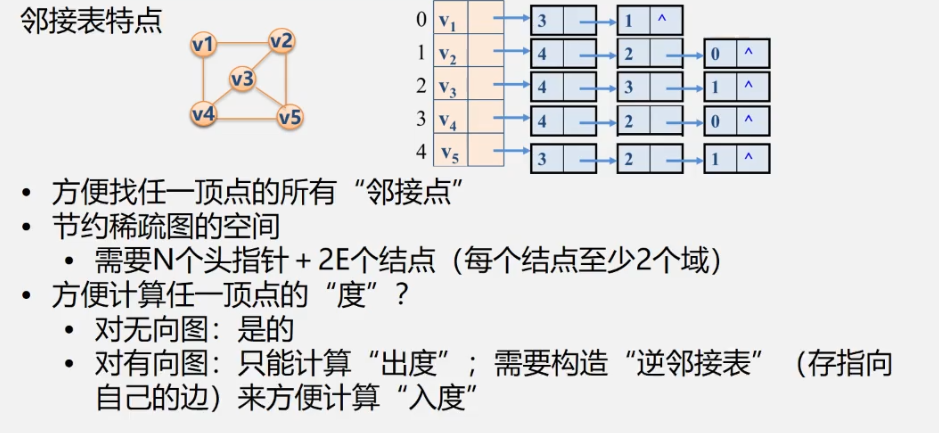
Adjacency list representation (chain)

• Vertex: stores vertex data in a one-dimensional array in numbered order
• Edges associated with the same vertex (arc with vertex as tail): stored in a linear linked list

Undirected graph

characteristic:

• Adjacency table is not unique
• If there are n vertices and e edges in an undirected graph, the adjacency table needs n head nodes and 2e table nodes. Suitable for storing sparse graphs
• The degree of vertex vi in undirected graph is the number of nodes in the ith single linked list

 

Directed graph

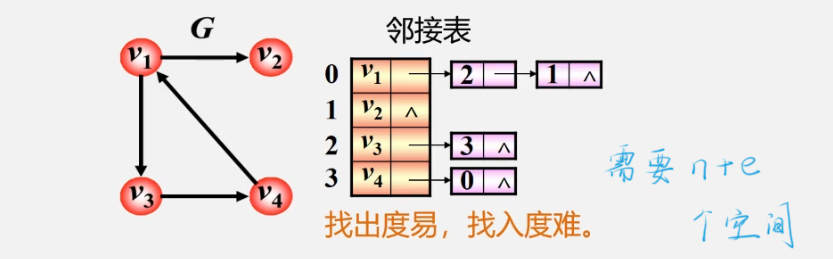
characteristic:

• The i-th vertex of vi is the number of vertices in the list
• The penetration of vertex vi is the number of nodes in the whole single linked list whose adjacent point field value is i - 1 (the whole linked list needs to be traversed)
   

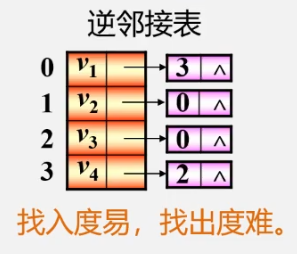
characteristic:

• The penetration of vertex vi is the number of nodes in the ith single linked list
• The outgoing degree of vertex vi is the number of nodes in the whole single linked list whose adjacent point field value is i - 1 (the whole linked list needs to be traversed)

 

 

Adjacency table storage representation of graph

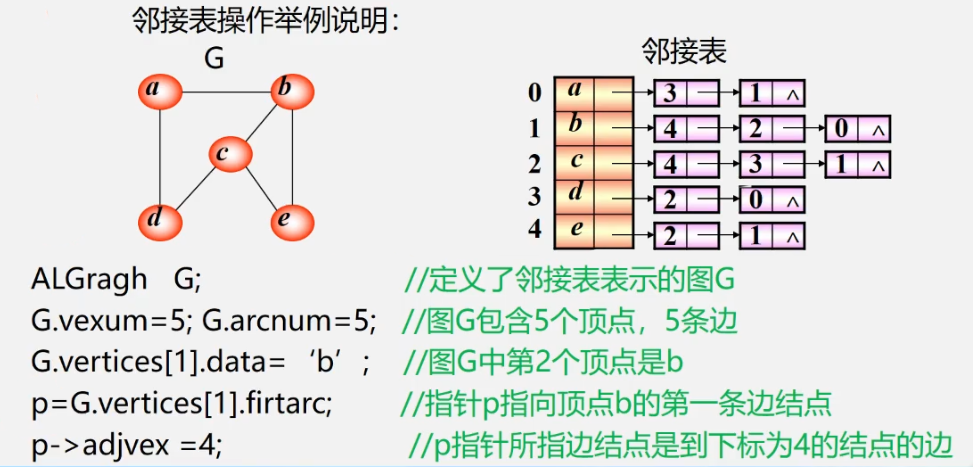
typedef struct VNode{
	VerTexType data;		//Vertex information
	ArcNode * firstarc;		//Pointer to the first edge attached to the vertex
}VNode, AdjList[MVNum]		//AdjList indicates the adjacency table type

Description: for example, AdjList v;    equivalent to: VNode v[MVNum];

#define MVNum 100 				// max vertex 
typedef struct ArcNode{			//Edge node
	int adjvex;					//The position of the vertex that the edge points to		
	struct ArcNode * nextarc;	//Pointer to the next edge
	OtherInfo info;				//Information domain; Store edge related information
}ArcNode;

Structure definition of drawing:

typedef struct{
	AdjList vertices;		//Vertices -- the plural of vertex
	int vexnum, arcnum;		//Current vertex number and arc number of graph
}ALGraph;

 
 

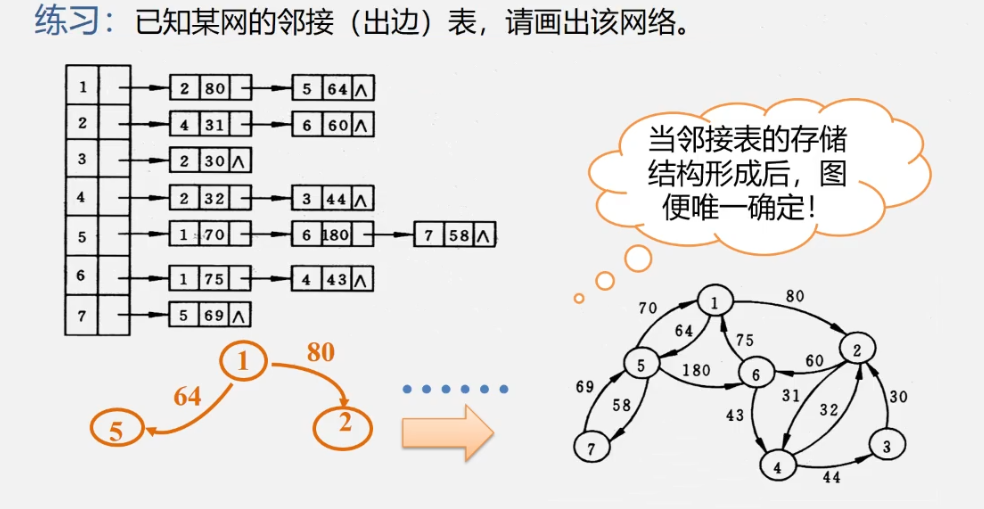
Using adjacency table representation to create undirected network

Algorithm idea:

1. Enter the total number of vertices and edges
2. Create vertex table
   Input the information of points in turn and store it in the vertex table
   Initialize the pointer field of each header node to NULL
3. Create adjacency table
   Enter the two vertices to which each edge is attached in turn
   Determine the sequence numbers i and j of the two vertices and establish the edge node
   Insert this edge node into the head of the two edge linked lists corresponding to vi and vj respectively

//Using adjacency table representation, undirected graph G is created
Status CreateUDG(ALGraph &G){
	cin >> G.vexnum >> G.arcnum;		//Enter the total number of vertices and edges
	
	for(i = 0; i < G.vexnum; ++i){		//Input each point to construct the header node table
		cin >> G.vertices[i].data;		//Enter vertex value
		G.vertices[i].firstarc = NULL;	//Initializes the pointer field of the header node
	}//for
	
	for(k = 0; k < G.arcnum; ++k){		//Input each edge to construct the adjacency table
		cin >> v1 >> v2;				//Enter the two vertices to which an edge is attached
		i = LocateVex(G, v1);
		j = LocateVex(G, v2);
		p1 = new ArcNode;				//Generate a new edge node * p1
		p1 -> adjvex = j;				//The serial number of adjacent points is j
		p1 -> nextarc = G.vertices[i].firstarc;
		G.vertices[i]firstarc = p1;		//Insert the new node * p1 into the edge table header of vertex vi
		p2 = new ArcNode;				//Generate another symmetrical new edge node * p2
		p2 -> adjvex = i;				//The number of adjacent points is i
		p2 -> nextarc = G.vertices[j].firstarc;
		G.vertices[j].firstarc = p2;	//Insert the new node * p2 into the edge table header of vertex vj
	}//for
	return OK;
}

 
 

Relationship between adjacency matrix and adjacency table representation

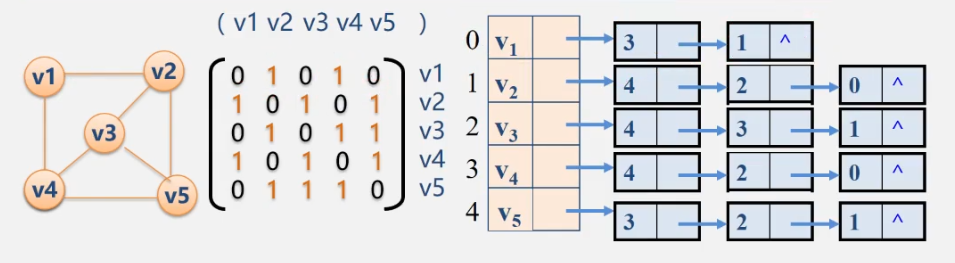
1. Connection: each linked list of adjacency list corresponds to a row in the adjacency matrix. The number of nodes in the linked list is equal to the number of non-zero elements in a row
2. difference:
   ① For any definite undirected graph, the adjacency matrix is unique (the row and column number is consistent with the vertex number), but the adjacency table is not unique (the link order is independent of the vertex number)
   ② The spatial complexity of adjacency matrix is O(n2), while the spatial complexity of adjacency table is O(n+e)
3. Usage: adjacency matrix is mostly used for dense graphs; Adjacency tables are mostly used in sparse graphs

 
 

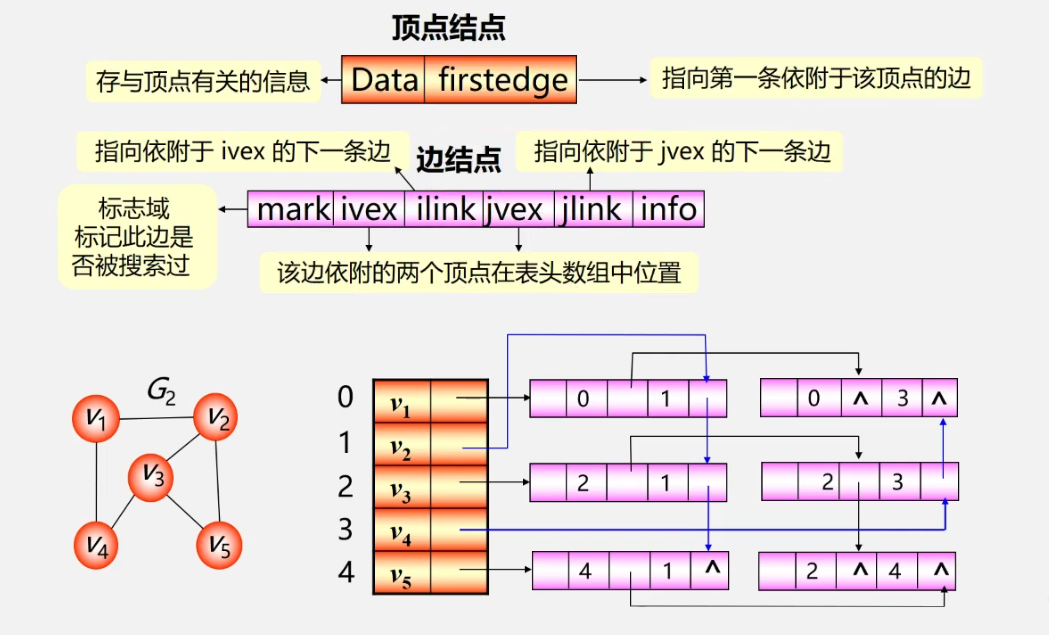
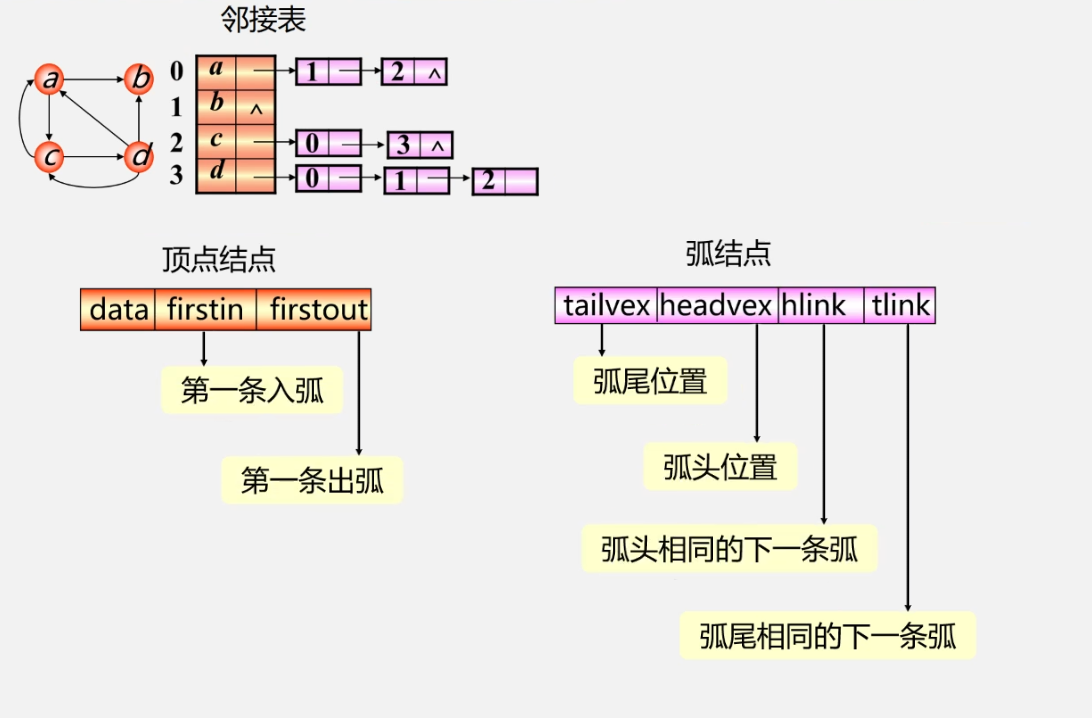
Cross linked list - for directed graphs

   orthogonal list is another linked storage structure of directed graph, which can be regarded as a linked list formed by the combination of adjacent list and inverse adjacent list of directed graph

   each arc in a directed graph corresponds to an arc node in the cross linked list, and each vertex in a directed graph corresponds to a node in the cross linked list, which is called a vertex node
 


 
 

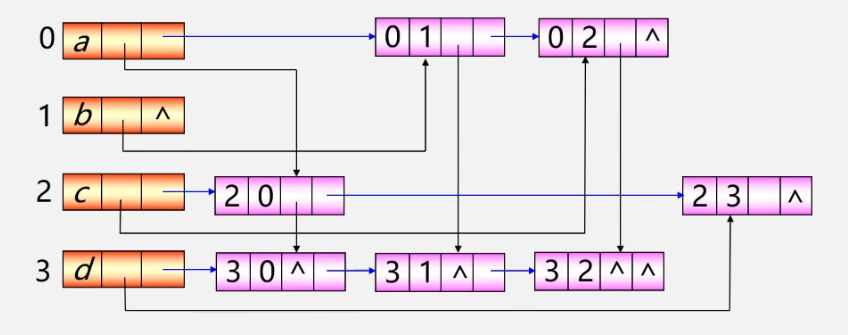
Adjacency multiple list (another chain storage structure of undirected graph)

Advantages of adjacency table: it is easy to obtain the information of vertices and edges
    disadvantages: some operations are inconvenient (for example, to delete an edge, you need to find two nodes representing the edge)

Adjacency multiple table: