preface
In the process of learning data structures or algorithms, we inevitably need to use sorting. The so-called sorting is to arrange the records in a certain order.
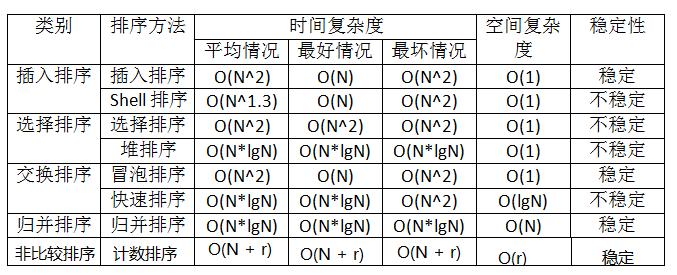
The data structure mainly introduces eight common sorts. Let's learn together this time.

Tip: the following is the main content of this article. The following explanation is for reference
Implementation of eight sorting algorithms
1. Insert sort (direct insert sort, Hill sort)
Core idea:
The sequence to be sorted is divided into ordered area and unordered area. One record in the unordered area is sorted and inserted in the ordered area, so that the length of the ordered area is + 1
(1) Insert sort directly:
Thought:
First, find the records to be inserted in the disordered area circularly and place them in the "sentry position", and then compare the last bit in the ordered area one by one. If it is large, move it to give way, if it is small, don't move until the insertion position is determined and inserted.
Dynamic diagram demonstration:
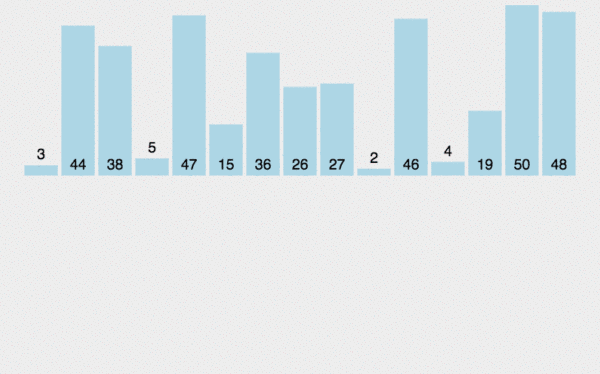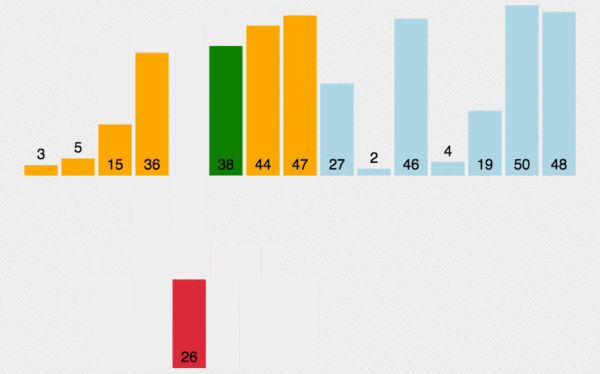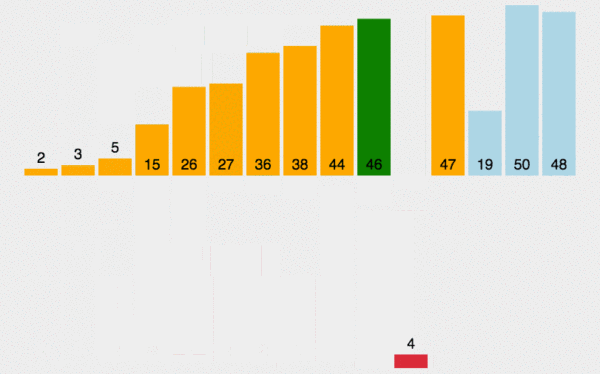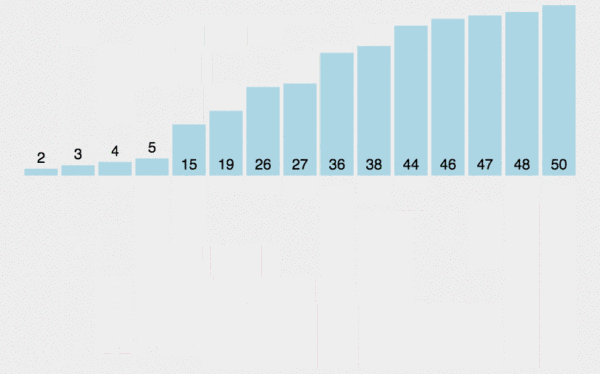
Reference code:
void InsertSort(RcdType &L) { //Direct insert sort on sequential table
int i,j;
for (i=1;i<L.length;++i) {
if (L.rcd[i].key>L.rcd[i+1].key) {
//Loop to find the record L.rcd[i+1] to be inserted in the unordered area
//Store it in the "sentry position"
L.rcd[0] = L.rcd[i+1];
j = i+1;
while (L.rcd[j-1].key>L.rcd[0].key) {
L.rcd[j] = L.rcd[j-1];
j--;
}
L.rcd[j] = L.rcd[0]; //insert
}
}
}
(2) Hill sort:
Hill sort is an improvement of direct insertion sort, but it is also an unstable sort algorithm.
Thought:
Treat the sequence to be sorted as an equal difference sequence, select several sub sequences according to a certain tolerance, directly insert and sort each sub sequence, reduce the tolerance in turn, and repeat the above operations until the tolerance is 1
Dynamic diagram demonstration:
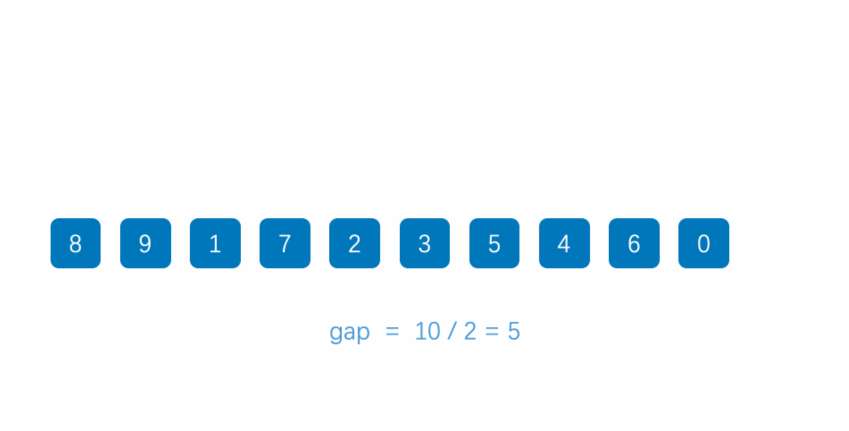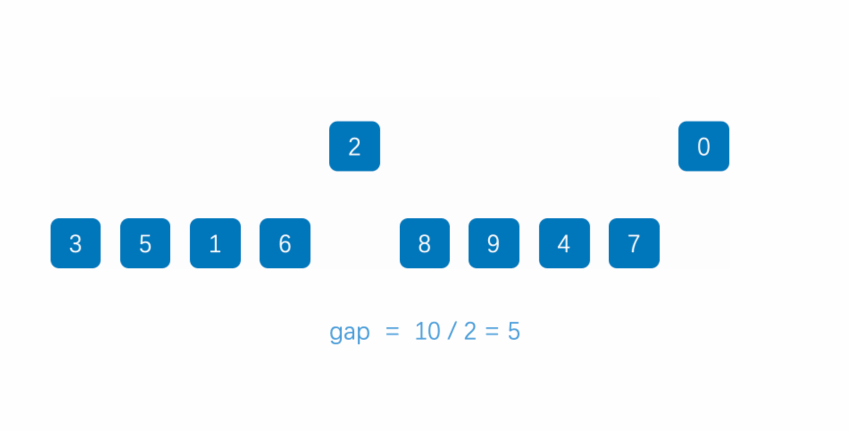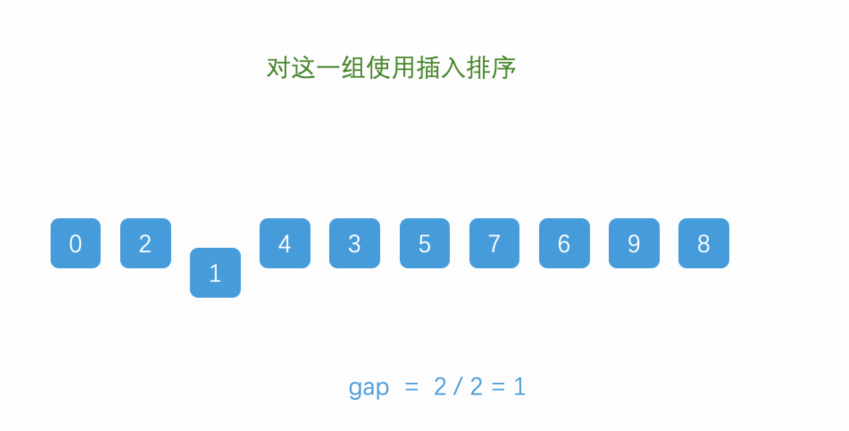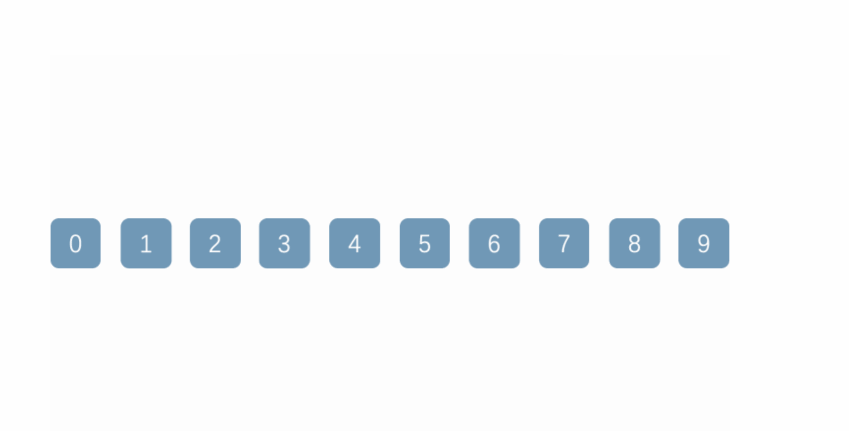
Reference code:
Sort by type:
//Make a hill sort on the sequence table with an increment of D (which can be understood as tolerance)
void ShellInsert(RcdSqList &L,int d) {
int i,j;
for (i=1;i<L.length-d;++i) {
if (L.rcd[i].key>L.rcd[i+d].key) {
//Loop to find the record L.rcd[i+d] to be inserted in the unordered area
//Store it in the "sentry position"
L.rcd[0] = L.rcd[i+d];
j = i+d;
while (L.rcd[j-d].key>L.rcd[0].key) {
L.rcd[j] = L.rcd[j-d];
j--;
}
L.rcd[j] = L.rcd[0]; //insert
}
}
}
It can be seen that the code of Hill sort is highly similar to that of direct insertion sort. In fact, direct insertion sort can be regarded as Hill sort with increment of 1.
Hill sort:
void ShellSort(RcdSqList &L,int d[],int t) {
//Sort the sequential Table L according to the incremental sequence d[0...t-1]
int k;
for (k=0;k<t;k++) {
ShellInsert(L,d[k]); //Insert sort with one increment of d[k]
}
}
2. Select sort (simple select sort, heap sort)
**Idea: * * selective sorting refers to selecting the record with the smallest keyword in the unordered area and placing it at the end of the ordered area until all records are in order.
(1) Simple selection sorting:
Dynamic diagram demonstration:
Reference code:
void select_sort(int a[],int n) { //The number of elements to sort passed in to the array
int i,j,min,t;
for(i=0;i<n-1;i++) {
min=i; //min: current minimum subscript
for(j=i+1;j<n;j++) { //Scan the rest
if(a[min]>a[j]) //If any other element is smaller, its subscript is recorded
min=j;
if(min!=i) { //If the minimum value is not at the first place in the sorting area, change to the first place
t=a[min]; a[min]=a[i]; a[i]=t;
}
}
}
}
(2) Heap sort:
Core idea:
Construct the sequence to be sorted into a large top heap (or small top heap). At this time, the maximum (minimum) of the whole sequence is the root node at the top of the heap. Exchange it with the last element, and the end is the maximum (minimum) at this time. Then reconstruct the remaining n-1 elements into a heap, so as to obtain the sub small (sub large) values of n elements . if you execute it repeatedly, you can get an ordered sequence.
The large top heap is in ascending order and the small top heap is in descending order
Dynamic diagram demonstration:
3. Swap sort (bubble sort, quick sort)
Pairwise comparison (can be adjacent or not), reverse order exchange
(1) Bubble sorting
Idea: adjacent pairwise comparison, reverse order exchange
But here we should pay attention to the number and times of trips to be compared.
N records need to be compared n-1 times, just like two numbers only need to be compared once; the i-th time only needs to be compared n-i times (the comparison times after each trip will be reduced by one)
Dynamic diagram demonstration:
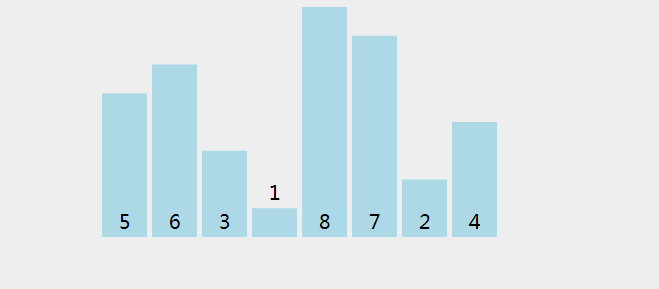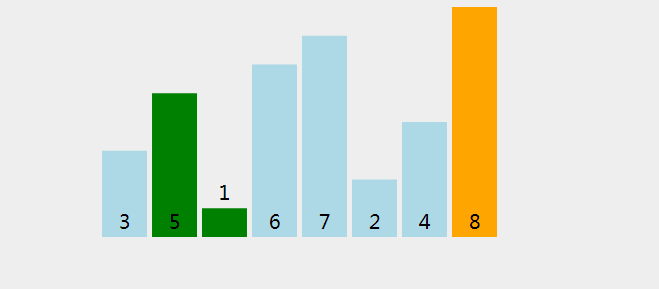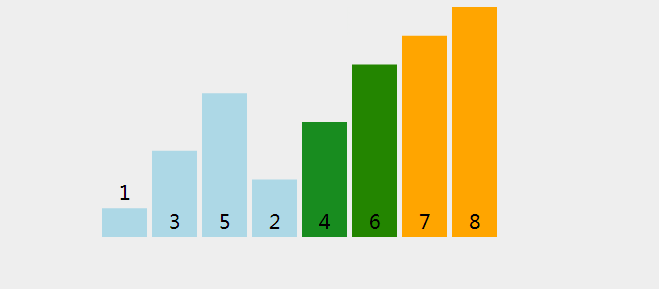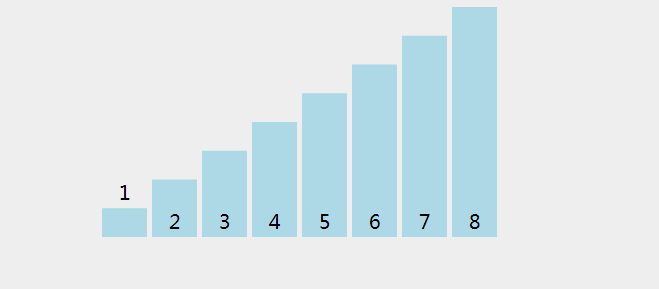
Reference code:
void bubble_sort(int a[], int n) { //The number of elements to sort passed in to the array
int i, j, t;
for (j=0; j<n-1; j++) { //N elements compare n-1 rounds
for (i= 0; i<n-1-j;i++) { //Compare two adjacent numbers
if(a[i]>a[i+1]) { //If the size order does not match, exchange
t=a[i]; a[i]=a[i+1]; a[i+1]=t;
}
}
}
}
(2) Quick sort
Dynamic diagram demonstration:
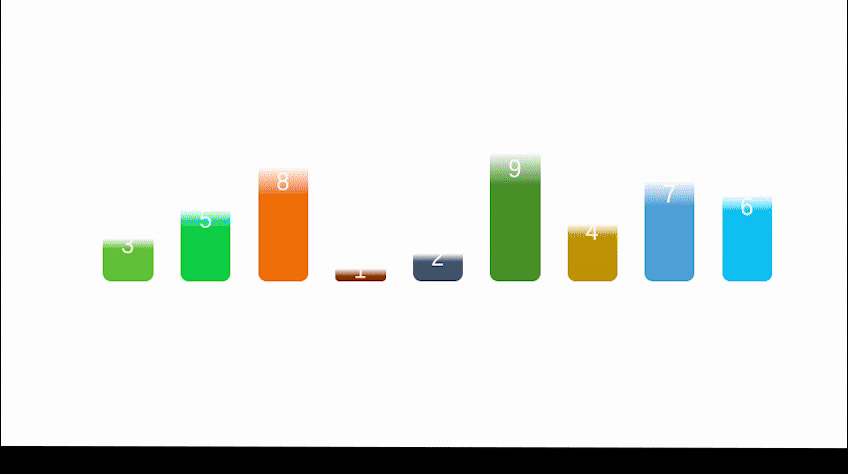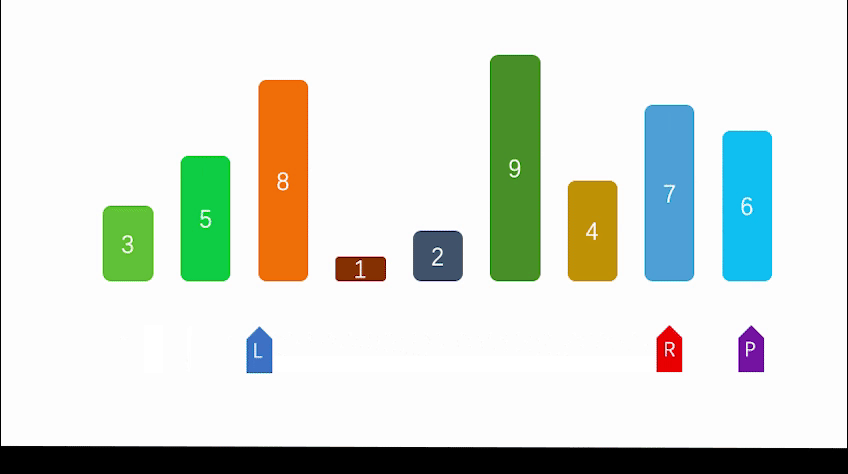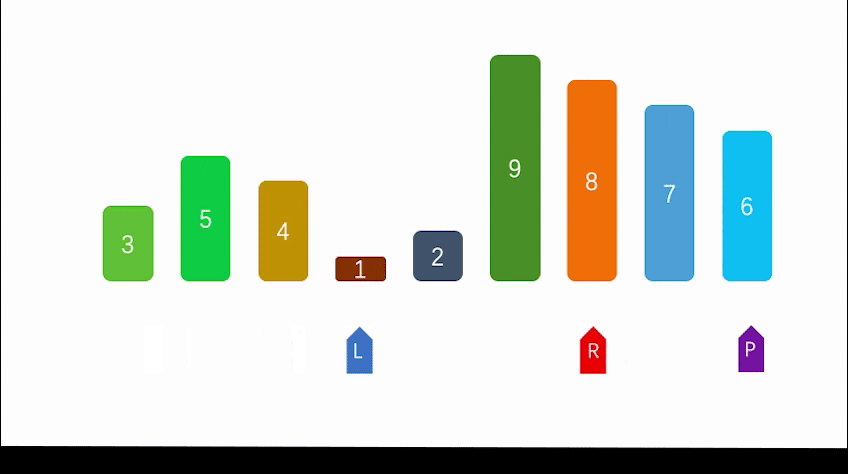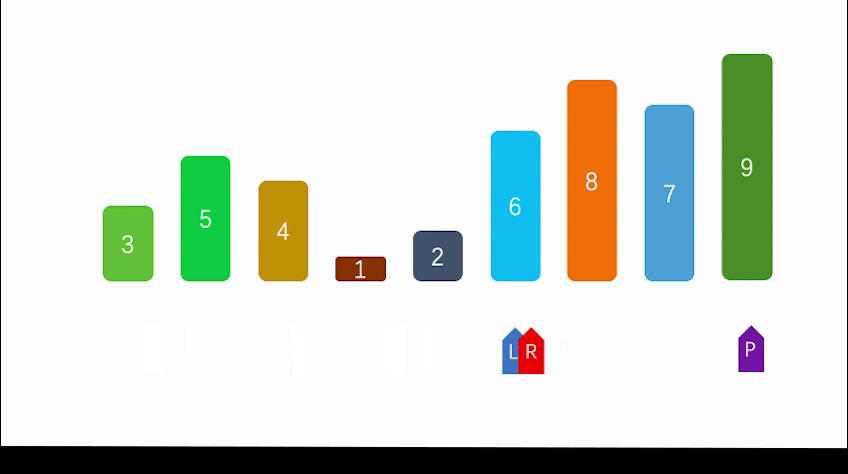
Reference code:
To quickly sort the order table L of records:
void QuickSort(RcdSqList &L) { //Quickly sort the order table L of records
QSort(L.rcd,1,L.length);
}
To quickly sort a record sequence rcd[s... t]:
void QSort (RcdType rcd[],int s,int t) {
//Quick sort of record sequence rcd[s...t]
int pivotloc ;
if (s<t) { //Length greater than one
pivotloc = Partition(rcd,s,t);
QSort(rcd,s,pivotloc-1);z
QSort(rcd,pivotloc+1,t) ;
}
}
Partition algorithm:
int Partition (RcdType rcd[],int low,int high) {
//Divide the subsequence rcd[low...high] once and return to the position where the pivot should be
//So that the keyword before the pivot is not greater than its keyword,
//No keyword after the pivot is less than its keyword
rcd[0] = rcd[low];
while (low < high) {
//low and high move alternately from both ends of the sequence to be sorted to the middle
while (low < high && rcd[high].key >= rcd[0].key) {
--high;
}
rcd[low] = rcd[high]; //Move keywords smaller than pivot keywords to the low end
while (low < high && rcd[low].key <= rcd[0].key) {
++low;
}
rcd[high] = rcd[low]; //Move keywords larger than pivot keywords to the high end
}
}
4. Merge sort
Core idea:
Divide the sequence to be sorted into several subsequences in equal proportion, repeat the above steps until the length of the subsequence is 1, and orderly merge each subsequence layer by layer to form an ordered sequence.
2-road merging:
Compare the size of the elements of the flag bit in the two subsequences respectively. The small one is moved to the large sequence, and the flag bit of the subsequence is + 1 (moved one bit later). When one subsequence is moved to the large sequence, and the other subsequence has elements, it is directly copied to the large sequence.Dynamic diagram demonstration:
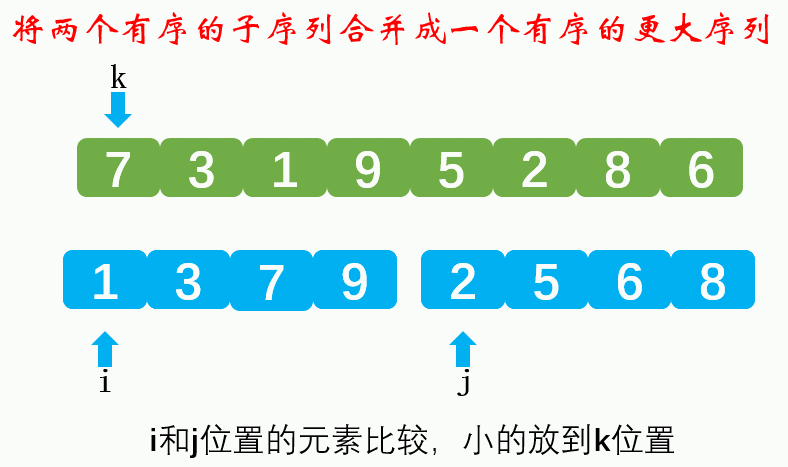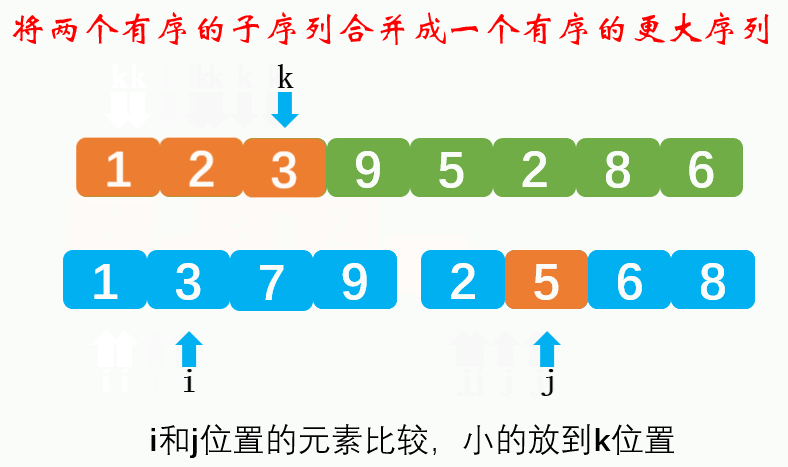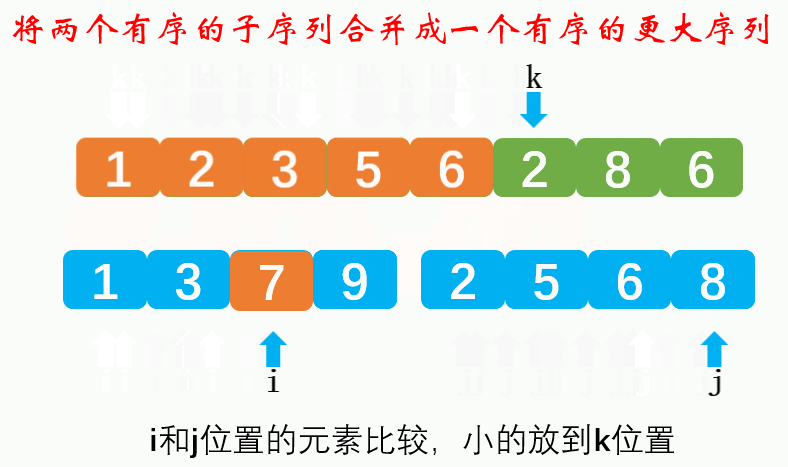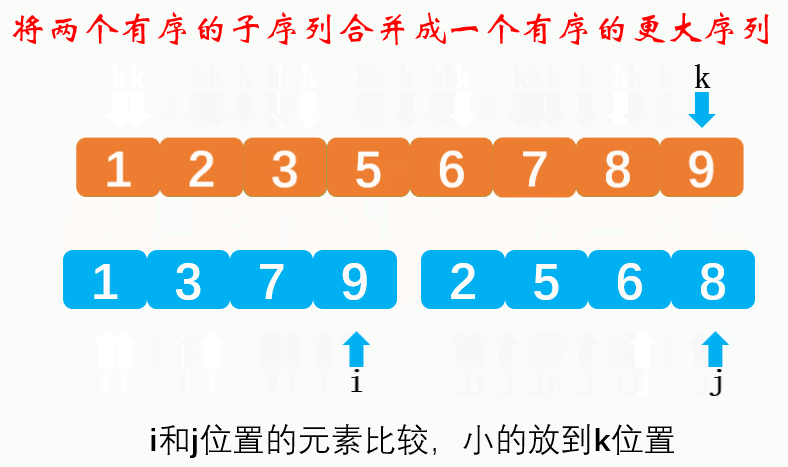
Reference code:
void Merge(RcdType SR[],RcdType TR[],int i,int m,int n) {
//Merge the adjacent ordered intervals SR[i..m] and SR[m+1...n] into ordered TR[i..n]
int k,j;
for (j = m+1,k=1;i<=m && j<=n;++k) {
//Records in SR are copied to TR from small to large by keyword
if (SR[i].key<=SR[j].key) {
//Note here that if < = is changed to <, the merge sort is unstable
TR[k] = SR[i++] ;
}
else {
TR[k] = SR[j++] ;
}
}
while (i<=m) { //Copy remaining SR[i..m] to TR
TR[k++] = SR[i++];
}
while (j<=n) { //Copy remaining SR[j..n] to TR
TR[k++] = SR[j++];
}
}
Recursive merge sort:
Dynamic diagram demonstration:

Reference code:
void MSort(RcdType R1[],RcdType R2[],int i,int s,int t) {
//Merge and sort R1[s..t]. If i%2==1, the sorted records are stored in R2[s...t],
//Otherwise, it is stored in R1[s..t]
int m;
if (s == t) { //At this time, the subsequence length is 1
if (1 == i%2) {
//The sorting process uses R1 and R2 alternately, and finally returns to R1
//That's why I have this requirement
R2[s] = R1[s];
}
}
else {
m = (s+t)/2; //split
MSort(R1,R2,i+1,s,m);
MSort(R1,R2,i+1,m+1,t);
if (1 == i%2) {
Merge(R1,R2,s,m,t); //Merge
}
else {
Merge(R2,R1,s,m,t);
}
}
}
2-way merge and sort the sequence table:
void MergeSort(RcdSqList &L) {
//2-way merge and sort the sequence table L
RcdType *R;
//Apply for auxiliary space
R = (RcdType*)malloc((L.lenght+1)*sizeof(RcdType));
//Merge and sort L.rcd[1..L.lenght]
MSort(L.rcd,R,0,1,L.lenght);
free(R);
}
5. Cardinality sort
Core idea:
(for better understanding, let's take a three digit keyword as an example, such as 321)
The keyword "312" can be regarded as a combination of multiple keywords, i.e. single digit, ten digit and hundred digit. If you start from the lowest (single digit) keyword, first "allocate" the records to r subsequences according to different values of the keyword, and then "collect" each subsequence from small to large, and repeat m times (the keyword composed of M keywords) Finally, the sorting of the whole record is completed.
Dynamic diagram demonstration:
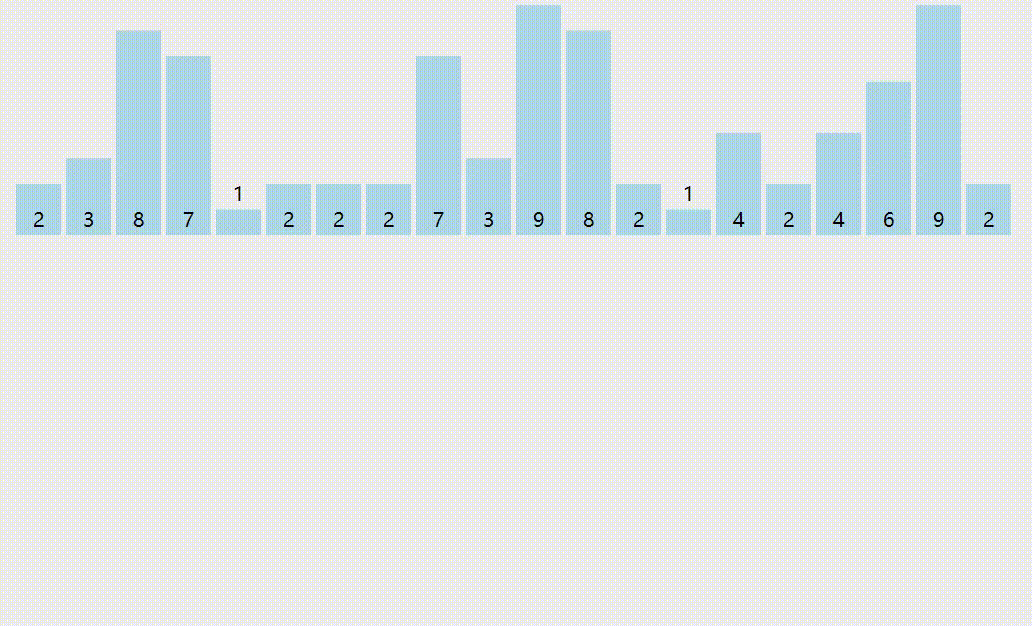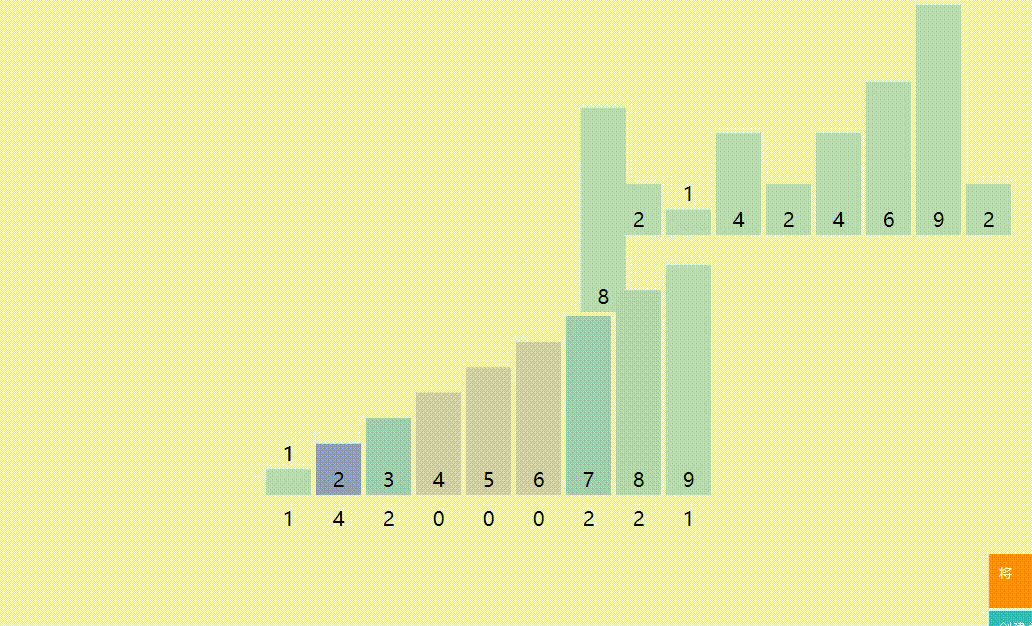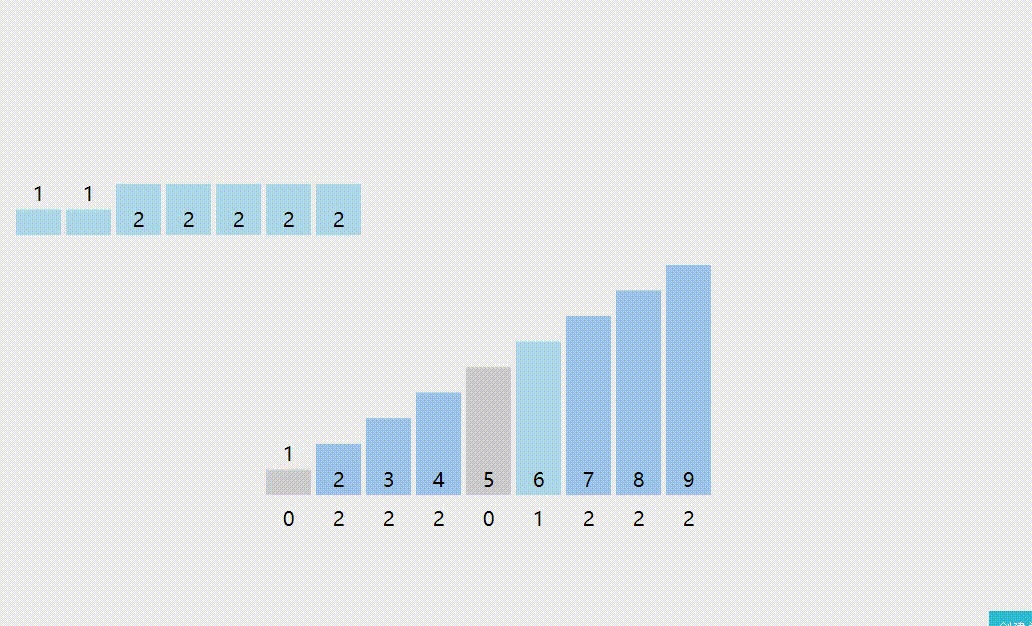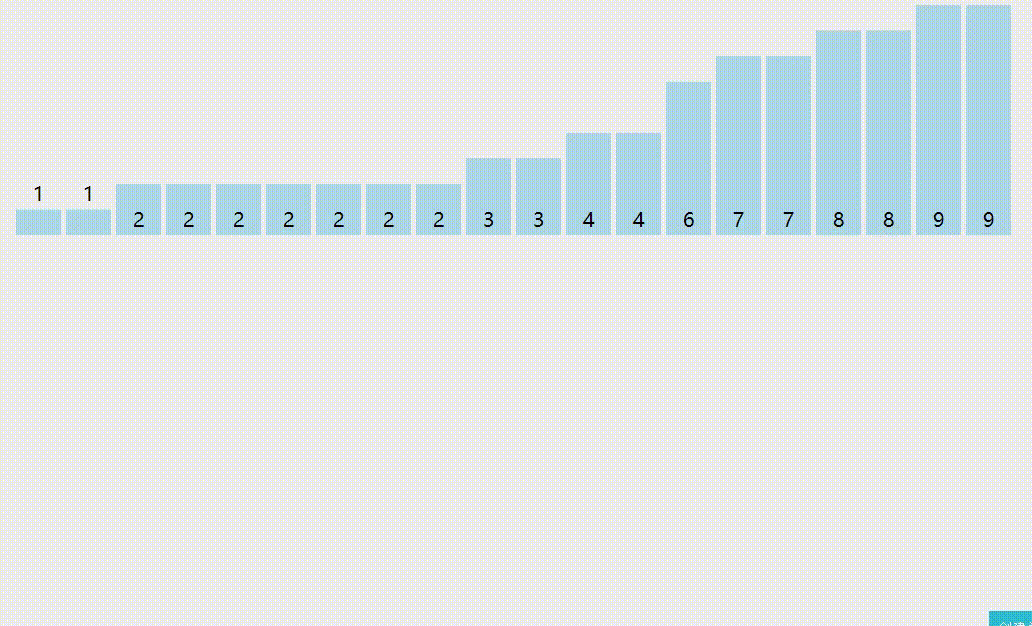

Reference code:
//One pass cardinality sorting
void Radixpass(KeysRcdType rcd[],KeysRcdType rcd[],int n,int i,int count[],int pos[],int radix) {
//Count the ith bit of the record keyword in the array rcd and calculate the starting position array pos []
//And copy the records in RCD into array rcd1 according to pos [] array
int k,j;
for (k=1;k<=n;k++) {
count[rcd[k].keys[i]]++; //Count various values
}
pos[0] = 1;
for (j=1;j<radix;++j) {
pos[j] = count[j-1] + pos[j-1]; //Find the starting position
}
for (k=1;k<=n;k++) { //collect
j = rad[k].keys[i];
rcd1[pos[j]++] = rcd[k]; //Copy record, corresponding to starting position + 1
}
}
summary