Write before
In fact, you've updated a note about the balanced tree before;-> Note links;
Learn Data Structure Notes (12) [Balanced Binary Search Tree (AVLTREE)]
The previous implementation required the index of the parent node of the current node to be calculated;... The steps for the implementation of left-handed and right-handed are relatively clear.
The disadvantage is that only the balance of the binary tree is maintained when adding nodes.
This time the operation method of the balance tree is slightly different from the previous one. So make a note of it...
The base here will be changed based on the previous implementation of the binary search tree. Note Links - >
Data Structure (5) [Binary Search Tree (Java)]
Here, the attribute heights are first defined within the node to represent the height.
Then define the base method in the tree to get the height of the tree.
The basic method obtains the balance factor of the tree: -> the height difference between left and right subtrees;
Defines a method to determine whether the current tree is a binary search tree (to determine whether the results of the middle-order traversal are sorted from small to large);
Whether the current tree is a balance tree (if the balance factor exceeds 1);
The left-to-right operation maintains the balance of the binary tree when adding/deleting nodes;
As shown, this is not a balance tree
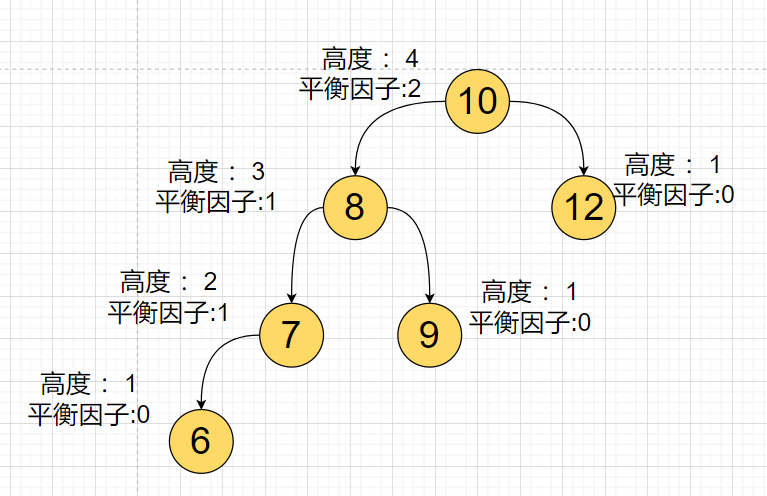
Right Rotation
The left subtree of this tree is high; To rotate right
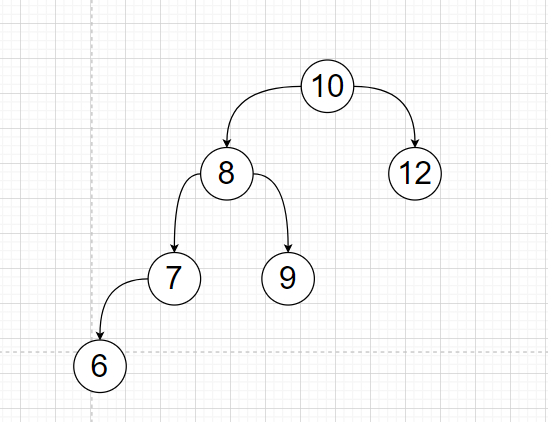
Then, it only takes two steps;
First, the right child node 9 of node 8 will be removed. Node 10 as the right child of Node 8
Then let node 9 be the left child of node 10
Left Rotation
This tree has a high right subtree and needs to be rotated to the left
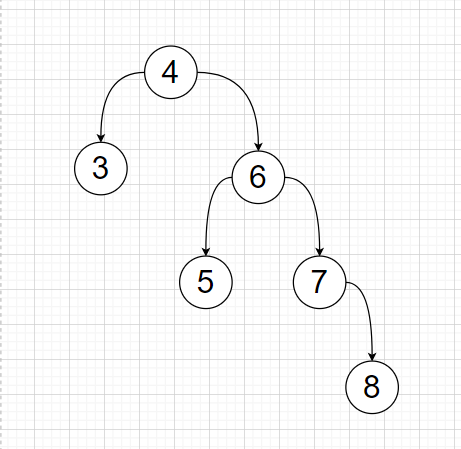
Only two steps;
First, the left child node 5 of node 6 is removed and recorded.
Node 4 as the left child of Node 6
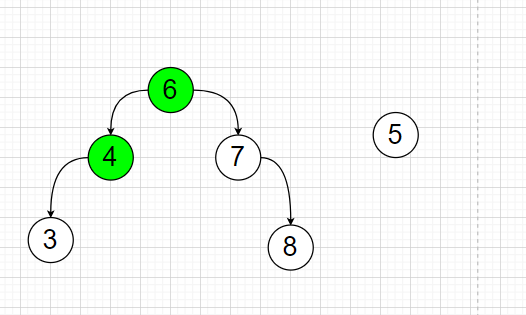
Node 5 is then used as the right child of Node 4
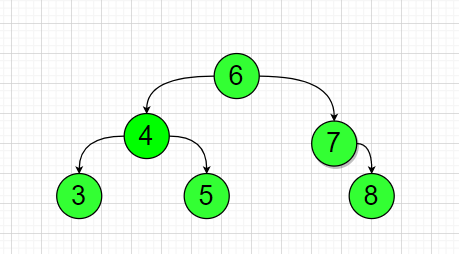
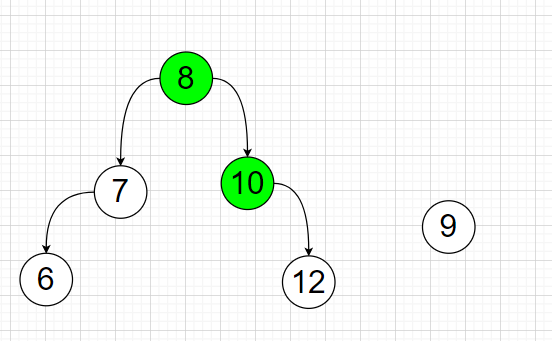
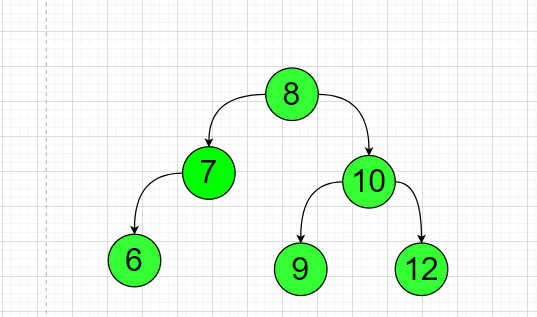
Double Rotation
If there is a special case, the double-rotating motion is obtained.
Like the following, it needs to be rotated left first. Then rotate to the right;
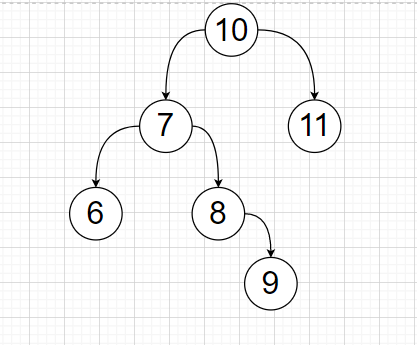
Rotate node 7 left first
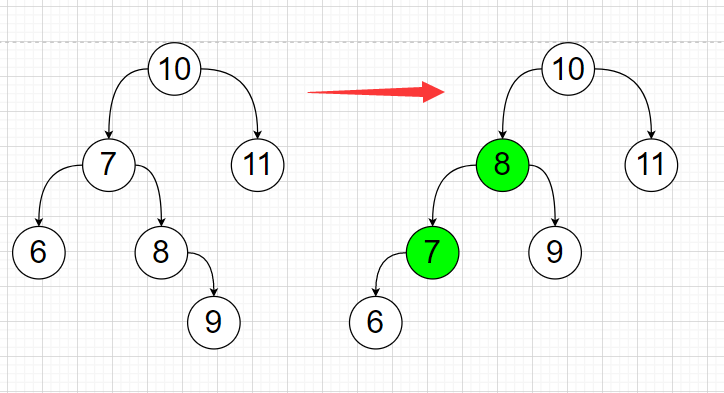
Then rotate node 10 to the right
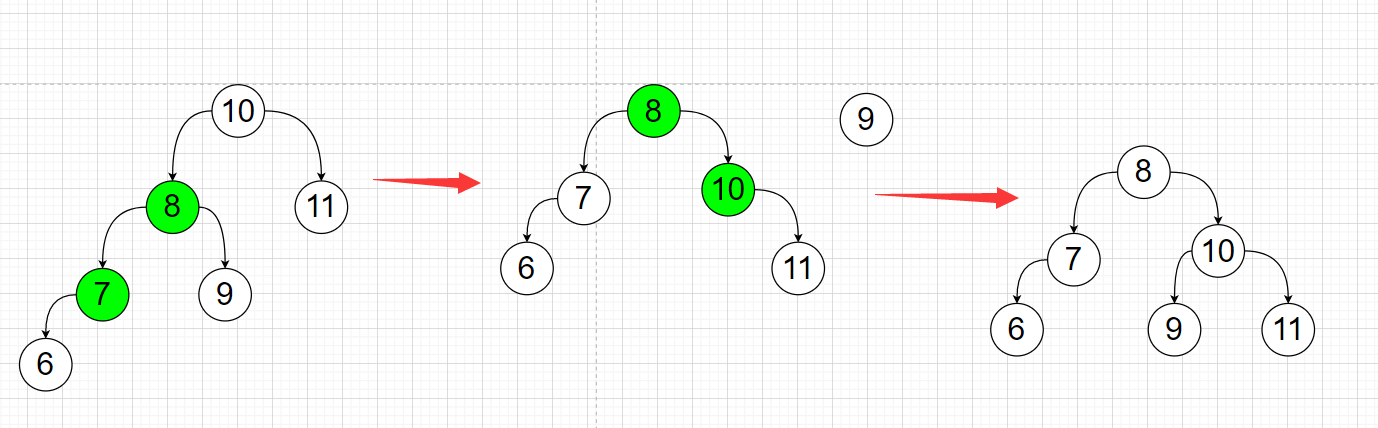
Specific code
package com.company.e_avltree;
import java.util.*;
/**
* @author Smart RE0
* @Date: 2021/12/10/
*/
//Because of the binary search tree, you need to compare the size of the elements;
public class AVLStartTree<T extends Comparable<T>> {
//Define internal class nodes;
class Node {
T val;
//Left subtree, right subtree;
Node leftNode;
Node rightNode;
//The height of the tree;
int height;
public Node(T val) {
//At initialization, the height of the tree is 1;
this.height = 1;
this.val = val;
this.leftNode = null;
this.rightNode = null;
}
}
//Define the root node of the tree;
private Node root;
//Define the number of tree nodes;
private int size;
public AVLStartTree() {
this.root = null;
this.size = 0;
}
//Empty sentence;
public boolean isEmpty() {
return this.root == null;
}
/**
* Gets the height of the tree with the specified node
*
* @param node node
*/
public int getHeight(Node node) {
if (node == null) {
return 0;
} else {
return node.height;
}
}
/**
* Gets the height factor of the tree starting from the specified node; The height difference between left and right subtrees;
*/
public int getHeightFactor(Node node) {
if (node == null) {
return 0;
}
//There is no absolute value here, there may be a negative height factor
return getHeight(node.leftNode) - getHeight(node.rightNode);
}
/**
* Determine if it is a binary search tree;
*/
public boolean isBSTTree() {
return isBSTTree(root);
}
/**
* Determine whether it is a binary search tree
*/
private boolean isBSTTree(Node node) {
List<T> values = new ArrayList<>();
//Call a recursive method; Store values in values;
inordertraversal(node, values);
//Traversing through the traversed values, if it is a binary tree, will actually sort from small to large, if not, it will end directly;
//Be careful; Since the current node is compared with the latter, the number of loops is actually less than once;
for (int i = 0; i < values.size() - 1; i++) {
//If the front is larger than the back, go back directly.
if (values.get(i).compareTo(values.get(i + 1)) > 0) {
return false;
}
}
return true;
}
/**
* Medium-order traversal, saving traversal values into a set
*
* @param node node
* @param values Traversed values
*/
private void inordertraversal(Node node, List<T> values) {
//Recursive termination condition;
if (node == null) {
return;
}
//Left, middle and right;
inordertraversal(node.leftNode, values);
values.add(node.val);
inordertraversal(node.rightNode, values);
}
/**
* Determine whether it is a balance tree or not;
*/
public boolean isAVLTree() {
return isAVLTree(root);
}
/**
* Determine whether it is a balanced tree
*
* @param node node
*/
private boolean isAVLTree(Node node) {
//Conditions for recursive termination;
if (node == null) {
return true;
}
//Determine the balance factor of the current node;
if (Math.abs(getHeightFactor(node)) > 1) {
return false;
}
//Recursively calculates the height factor of the left and right subtrees.
return isAVLTree(node.leftNode) && isAVLTree(node.rightNode);
}
/**
* Left Rotation Processing
*
* @param curNode Current Node
*/
public Node RotateLeft(Node curNode) {
//Gets the right child node of the current node;
Node rNode = curNode.rightNode;
//Remove the left child node of the right child node and mark it.
Node rLNode = rNode.leftNode;
//Make the current node the left child of its right child node;
rNode.leftNode = curNode;
//Connect the left child node of the right child node of the current node to the right child node of the current node.
curNode.rightNode = rLNode;
//Change the height of the tree;
curNode.height = Math.max(getHeight(curNode.leftNode), getHeight(curNode.rightNode)) + 1;
rNode.height = Math.max(getHeight(rNode.leftNode), getHeight(rNode.rightNode)) + 1;
return rNode;
}
/***
* Right Rotation Processing
* @param curNode Current Node
*/
public Node RotateRight(Node curNode) {
//Gets the left child node of the current node;
Node lNode = curNode.leftNode;
//Remove and mark the right child of the left child node;
Node lRNode = lNode.rightNode;
//Make the current node the right child of its left child node;
lNode.rightNode = curNode;
//Connect the right child node of the left child node of the current node to the left child node of the current node.
curNode.leftNode = lRNode;
//Change the height of the tree;
curNode.height = Math.max(getHeight(curNode.leftNode), getHeight(curNode.rightNode)) + 1;
lNode.height = Math.max(getHeight(lNode.leftNode), getHeight(lNode.rightNode)) + 1;
return lNode;
}
/**
* Add Elements
*
* @param ele Specified Element
*/
public void add(T ele) {
//Determine whether a node exists;
if (contains(ele) != null) {
return;
}
//Return the root node created each time;
root = add(root, ele);
this.size += 1;
}
//The bottom level of elements added recursively;
private Node add(Node node, T ele) {
//Create if it does not exist;
if (node == null) {
return new Node(ele);
}
//The added elements are compared to the previous root nodes;
if (ele.compareTo(node.val) > 0) {
node.rightNode = add(node.rightNode, ele);
} else {
node.leftNode = add(node.leftNode, ele);
}
//After adding; Need to update the current tree height, ----->Calculate the left and right subtree height + 1 as the current tree height;
node.height = Math.max(getHeight(node.leftNode), getHeight(node.rightNode)) + 1;
//Left, right, and left-right rotation judgment;
Node resNode = null;
//Maintain balance;
//Extremely left;
if (getHeightFactor(node) > 1 && getHeightFactor(node.leftNode) >= 0) {
//Direct right-handed;
resNode = RotateRight(node);
}
//Extremely right;
else if (getHeightFactor(node) < -1 && getHeightFactor(node.rightNode) <= 0) {
//Turn left directly;
resNode = RotateLeft(node);
}
//The left tree is higher first, and the right subtree is higher later.
else if (getHeightFactor(node) > 1 && getHeightFactor(node.leftNode) < 0) {
//Rotate left before right;
node.leftNode = RotateLeft(node.leftNode);
resNode = RotateRight(node);
}
//The right tree is higher first, and the left subtree is higher behind.
else if (getHeightFactor(node) < -1 && getHeightFactor(node.rightNode) > 0) {
//Rotate right then left;
node.rightNode = RotateRight(node.rightNode);
resNode = RotateLeft(node);
} else {
//If it is balanced, the value of the node is used directly.
resNode = node;
}
return resNode;
}
/**
* Delete the specified value;
* @param val Specify a numeric value;
*/
public T removeAssignVal(T val) {
if (root == null) {
System.out.println("An empty tree does not need to be deleted");
return null;
}
//Find out if it exists first; To create a new method;
Node node = findAssignNode(root, val);
//Whether found or not;
if (node != null) {
//The deleted remaining nodes are hung after the root node.
root = removeAssignVal(root, val);
//The number of elements decreases;
this.size -= 1;
return node.val;
}
return null;
}
/**
* Deletes the underlying implementation of the specified node; Deletes the specified node in a binary tree with a root node of node.
*
* @param node Specify Root Node Start
* @param val Specify Value
*/
private Node removeAssignVal(Node node, T val) {
//When a node is found;
if (node.val.compareTo(val) == 0) {
//The first case==>The left tree of the deleted node is empty;
if (node.leftNode == null) {
//After deleting the current node; Hang the right subtree behind the original to the deleted node position;
Node RNode = node.rightNode;
node.rightNode = null;
return RNode;
}
//In the second case, the right tree is empty;
else if (node.rightNode == null) {
//After deleting the current node; Hang the left subtree behind the original to the deleted node position;
Node LNode = node.leftNode;
node.leftNode = null;
return LNode;
} else {
//Situation three; When neither the left tree nor the right tree is empty, you can choose to find the preceding node (the maximum value in the area of the left subtree) or the succeeding node (the minimum value in the area of the right subtree) instead of deleting the node.
//Select to find the successor node here;
Node minR = findMinNodeRecurve(node.rightNode);
Node minRNode = removeMinNode(node.rightNode);
//Subsequent nodes are placed at the deleted node location;
minR.leftNode = node.leftNode;
minR.rightNode = minRNode;
node.leftNode = null;
node.rightNode = null;
return minR;
}
}
//Recursion;
//When finding nodes, if the current root node is larger than the specified value, go to the left. Otherwise, go to the right;
if (node.val.compareTo(val) > 0) {
node.leftNode = removeAssignVal(node.leftNode, val);
} else {
node.rightNode = removeAssignVal(node.rightNode, val);
}
Node resNode = node;
//Update height;
resNode.height = Math.max(getHeight(resNode.leftNode),getHeight(resNode.rightNode))+1;
//Maintain balance operation;
//Extremely left;
if (getHeightFactor(resNode) > 1 && getHeightFactor(resNode.leftNode) >= 0) {
//Direct right-handed;
resNode = RotateRight(resNode);
}
//Extremely right;
else if (getHeightFactor(resNode) < -1 && getHeightFactor(resNode.rightNode) <= 0) {
//Turn left directly;
resNode = RotateLeft(resNode);
}
//The left tree is higher first, and the right subtree is higher later.
else if (getHeightFactor(resNode) > 1 && getHeightFactor(resNode.leftNode) < 0) {
//Rotate left before right;
resNode.leftNode = RotateLeft(resNode.leftNode);
resNode = RotateRight(resNode);
}
//The right tree is higher first, and the left subtree is higher behind.
else if (getHeightFactor(resNode) < -1 && getHeightFactor(resNode.rightNode) > 0) {
//Rotate right then left;
resNode.rightNode = RotateRight(resNode.rightNode);
resNode = RotateLeft(resNode);
}
return resNode;
}
//Traverse in middle order; Modify slightly so that the traversal result is stored in a string;
public List<String> middleOrder() {
//If the binary tree is empty, null values are returned directly.
if (root == null) {
return null;
}
//The results of the traversal are stored in the set;
List<String> list = new ArrayList<>();
middleOrder(root, list);
return list;
}
//Traverse the bottom in middle order;
private void middleOrder(Node node, List<String> list) {
//The recursive end point stops when the last leaf node is reached;
if (node == null) {
return;
}
//Median Traverse=Traverse Left Subtree==>Get Middle Node==>Traverse Right Subtree
middleOrder(node.leftNode, list);
list.add(node.val + "<---Height factor--->" + getHeightFactor(node));
middleOrder(node.rightNode, list);
}
/**
* Output the middle traversal information of the print tree;
*/
@Override
public String toString() {
List<String> list = middleOrder();
list.forEach(a -> System.out.println(a + "\t"));
return "";
}
//Query elements;
public Node contains(T ele) {
if (root == null) {
return null;
}
return contains(root, ele);
}
//The bottom level of the query element;
private Node contains(Node root, T ele) {
//Recursive end point;
if (root == null) {
return null;
}
//Store the value of the current root node;
T val = root.val;
if (ele.compareTo(val) == 0) {
return root;
} else if (ele.compareTo(val) > 0) {
return contains(root.rightNode, ele);
} else {
return contains(root.leftNode, ele);
}
}
//Delete the smallest node;
public void removeMinNode() {
//Find the smallest element;
T minNode = findMinNodeRecurve();
if (minNode == null) {
System.out.println("An empty tree does not need to be deleted");
return;
}
System.out.println("The smallest node to delete is=>" + minNode);
// The root node of the deleted tree hangs on the original tree.
root = removeMinNode(root);
this.size -= 1;
}
//Delete the bottom implementation of the smallest node;
private Node removeMinNode(Node node) {
//Stop if it reaches the leftmost side;
if (node.leftNode == null) {
//The right subtree hangs to the delete node;
Node n = node.rightNode;
node.rightNode = null;
return n;
}
//Recursion;
node.leftNode = removeMinNode(node.leftNode);
return node;
}
//Recursively find the smallest element;
public T findMinNodeRecurve() {
if (root == null) {
return null;
}
return findMinNodeRecurve(root).val;
}
//Recursively find the bottom implementation of the smallest element;
private Node findMinNodeRecurve(Node root) {
//Recursive end point;
if (root.leftNode == null) {
return root;
}
return findMinNodeRecurve(root.leftNode);
}
/**
* Find the specified element starting from the current root node;
*
* @param node root node
* @param val Specify element values
*/
private Node findAssignNode(Node node, T val) {
//Return null value if not found;
if (node == null) {
return null;
}
//If the current node is the specified value;
if (node.val.compareTo(val) == 0) {
return node;
}
//The current root node is larger than the specified value. Depending on the nature of the binary search tree, the smaller one is found in the left subtree.
else if (node.val.compareTo(val) > 0) {
//Go to left subtree query;
return findAssignNode(node.leftNode, val);
} else {
//Exclude the above and go to the right subtree to find it.
return findAssignNode(node.rightNode, val);
}
}
}
Test Use
//Test use;
public static void main(String[] args) {
AVLStartTree<Integer> avlStartTree = new AVLStartTree<>();
Random random = new Random();
//Add elements;
avlStartTree.add(120);
for (int i = 0; i < 15; i++) {
avlStartTree.add(random.nextInt(1000));
}
//Delete elements;
avlStartTree.removeAssignVal(120);
System.out.println("Is it a binary search tree->" + avlStartTree.isBSTTree());
System.out.println("Is it a balanced tree->" + avlStartTree.isAVLTree());
System.out.println(avlStartTree);
}
test result
Is it a binary search tree->true Is it a balanced tree->true 60<---Height factor--->0 67<---Height factor--->0 100<---Height factor--->0 134<---Height factor--->0 147<---Height factor--->0 196<---Height factor--->-1 245<---Height factor--->0 348<---Height factor--->0 369<---Height factor--->0 382<---Height factor--->0 438<---Height factor--->-1 581<---Height factor--->0 771<---Height factor--->0 856<---Height factor--->-1 991<---Height factor--->0
Delete Method Optimization
/**
* Delete method optimization;
* Delete the specified value;
* @param val Specify a numeric value;
*/
public T removeAssignValOptimization(T val) {
if (root == null) {
System.out.println("An empty tree does not need to be deleted");
return null;
}
//Find out if it exists first; To create a new method;
Node node = findAssignNode(root, val);
//Whether found or not;
if (node != null) {
//The deleted remaining nodes are hung after the root node.
root = removeAssignValOptimization(root, val);
//The number of elements decreases;
this.size -= 1;
return node.val;
}
return null;
}
/**
* Delete method optimization;
* Deletes the underlying implementation of the specified node; Deletes the specified node in a binary tree with a root node of node.
*
* @param node Specify Root Node Start
* @param val Specify Value
*/
private Node removeAssignValOptimization(Node node, T val) {
Node resNode = null;
//When a node is found;
if (node.val.compareTo(val) == 0) {
//The first case==>The left tree of the deleted node is empty;
if (node.leftNode == null) {
//After deleting the current node; Hang the right subtree behind the original to the deleted node position;
Node RNode = node.rightNode;
node.rightNode = null;
resNode = RNode;
}
//In the second case, the right tree is empty;
else if (node.rightNode == null) {
//After deleting the current node; Hang the left subtree behind the original to the deleted node position;
Node LNode = node.leftNode;
node.leftNode = null;
resNode = LNode;
} else {
//Situation three; When neither the left tree nor the right tree is empty, you can choose to find the preceding node (the maximum value in the area of the left subtree) or the succeeding node (the minimum value in the area of the right subtree) instead of deleting the node.
//Select to find the successor node here;
Node minR = findMinNodeRecurve(node.rightNode);
//Call;
Node minRNode = removeAssignValOptimization(node.rightNode,minR.val);
//Subsequent nodes are placed at the deleted node location;
minR.leftNode = node.leftNode;
minR.rightNode = minRNode;
node.leftNode = null;
node.rightNode = null;
resNode = minR;
}
}
//Recursion;
//When finding nodes, if the current root node is larger than the specified value, go to the left. Otherwise, go to the right;
else if (node.val.compareTo(val) > 0) {
node.leftNode = removeAssignValOptimization(node.leftNode, val);
resNode = node;
} else {
node.rightNode = removeAssignValOptimization(node.rightNode, val);
resNode = node;
}
//To delete leaf nodes;
if(resNode ==null){
return null;
}
//Update height;
resNode.height = Math.max(getHeight(resNode.leftNode),getHeight(resNode.rightNode))+1;
Node finalNode = resNode;
//Maintain balance operation;
//Extremely left;
if (getHeightFactor(resNode) > 1 && getHeightFactor(resNode.leftNode) >= 0) {
//Direct right-handed;
finalNode = RotateRight(resNode);
}
//Extremely right;
else if (getHeightFactor(resNode) < -1 && getHeightFactor(resNode.rightNode) <= 0) {
//Turn left directly;
finalNode = RotateLeft(resNode);
}
//The left tree is higher first, and the right subtree is higher later.
else if (getHeightFactor(resNode) > 1 && getHeightFactor(resNode.leftNode) < 0) {
//Rotate left before right;
resNode.leftNode = RotateLeft(resNode.leftNode);
finalNode = RotateRight(resNode);
}
//The right tree is higher first, and the left subtree is higher behind.
else if (getHeightFactor(resNode) < -1 && getHeightFactor(resNode.rightNode) > 0) {
//Rotate right then left;
resNode.rightNode = RotateRight(resNode.rightNode);
finalNode = RotateLeft(resNode);
}
return finalNode;
}