Note: refer to Mr. Yan's data structure, implemented in c language, for self review

I summary

Some concepts and knowledge points

• Stability of sorting method

stability	characteristic
stable	For two records with the same keyword, their relative positions must remain unchanged before and after sorting
instable	The relative position of two records with the same keyword may change before and after sorting

• Different division of memory

classification	describe
Internal sorting	The records to be sorted are stored in the random access memory of the computer for sorting
External sorting	The number of records to be sorted is very large, and the memory cannot hold all records. During sorting, external memory needs to be accessed

• Classify the internal sorting methods according to different principles

classification
Insert sort
Exchange sort
Select sort
Merge sort
Count sort

• According to workload

classification	characteristic
Simple sorting method	Time complexity: O(n2)
Advanced sorting method	Time complexity: O(nlogn)
Cardinality sort	Time complexity: O(nd)

• Basic operations in sorting: compare and move

II Insert sort

2.1 direct insertion sort

• Basic idea: for a group of records: R[1... n], insert R[i] of i=2... n into the ordered arrangement of R[1... i-1].
• Key points:
  1. At the beginning of the cycle, an element of R[1] is regarded as an orderly arrangement and inserted successively from i=2.
  2. First, compare R[i] with R[i-1]: if R[i] > = R[i-1], it is orderly and does not need to be inserted. Otherwise, cycle to find the insertion position. (Note: the placement of equal sign judgment position shall meet its stability characteristics)
  3. Find the insertion position:
  4. R[0], as a monitoring post arranged, records R[i] in R[0] before looking for the insertion position of R[i] in R[1... I-1], so as to prevent information loss due to being overwritten by the record of R[i-1] when looking for the insertion position.
  5. j compares keywords with R[0] in reverse order from R[i-1] to R[1]. If R[j] is greater than R[0], R[j+1]=R[j] is assigned. At this time, R[j+1] records the original R[j] information, so it is not afraid that R[j] information will be overwritten and lost.
  6. It can be seen that after the above cycle, R[j] is the record with the first keyword equal to or less than R[0] from the back to the front. Then insert R[0] into the position of R[j+1].
  Note: j can also be inverted from i, and R[0] compares R[j-1]
• Algorithm analysis:

index	value	analysis
Space complexity T(n)	O(1)	Only auxiliary space R[0] is required
Time complexity S(n)	O(n2)	When the sequence to be sorted is positive, the number of comparisons is n-1 and the number of moves is 0; When the sequence to be sorted is in reverse order, the comparison times are ∑ i = 1 n − 1 i = n ( n − 1 ) 2 \sum_{i=1}^{n-1}i=\frac{n(n-1)}{2} Σ i=1n − 1 − i=2n(n − 1), the number of moves is ∑ i = 1 n − 1 i = n ( n − 1 ) 2 \sum_{i=1}^{n-1}i=\frac{n(n-1)}{2} Σ i=1n − 1 − i=2n(n − 1), n(n-1) in total; Take the average of the best case and the worst case as ( n + 1 ) ( n − 1 ) 2 \frac{(n+1)(n-1)}{2} 2(n+1)(n − 1), i.e. O(n2)

2.2 split insertion sort

• Basic idea: in order to make up for the defect of too many times of comparison and exchange when n is large in simple insertion sorting, starting from the number of comparison, replace the reverse search insertion position in simple insertion with the binary search insertion position, and then move the records behind the insertion position back uniformly after finding it.
• algorithm analysis

index	value	analysis
Spatial complexity	O(1)	low, high and m are required
Time complexity	O(n2)	Half search only reduces the number of comparisons, but not the number of exchanges. The main part that determines the time complexity in direct insertion sorting is the number of exchanges, so it is still O(n2)

2.3 2-way insertion sort

• Basic idea: improve on the basis of half search to reduce the number of exchanges. Let the auxiliary space vector with n records d[1... N], and d[1]=R[1]. Then traverse R[2... N], smaller than d[1], insert it in front of d[1] (the element in front of the insertion position moves forward), otherwise insert it behind d[1] (the element behind the insertion position moves backward). If D is regarded as a cyclic vector and two pointers first and final are set, then the "front" element of d[1] is d[first]~d[n], then d[1], and then the "back" is d[2]~d[final].
• algorithm analysis

index	value	analysis
Spatial complexity	O(n)	d[1... n] is required as an auxiliary vector
Time complexity	O(n2)	In fact, the number of exchanges is reduced to about n 2 8 \frac{n^2}{8} 8n2, but it is still N2 order, and when d[1] is the minimum record or the maximum record, it completely loses its superiority

2.4 table insertion sort

• Storage structure of static linked list

# define SIZE 100 	// Static linked list capacity
typedef struct{
	RcdType rc;		//Record item
	int		next;	//Pointer item
}SLNode;			//Table node type
typedef struct{
	SLNode r[SIZE];	//Unit 0 is the header node
	int length；	//Length of static linked list
}SLinkListType;		//Static linked list type

• basic thought
  1. The keyword of element 0 takes the maximum integer MAXINT and forms a circular linked list with element 1: R [1] next=0; r[0]. next=1;
  2. Insert the nodes of r[2... n] into the circular linked list logically by modifying the pointer (without modifying the storage location of the record)
  3. In order to realize random search, the records are rearranged according to the pointer of the linked list to realize the consistency between the storage location and the logical sequence.
• algorithm

  1. Sequential insertion of circular linked list (omitted)

  2. Rearrange

      Key points:
      	 For a record that has been arranged, its next The value is the position to which the records in the original position are exchanged when it is put here. In this way, when you continue to arrange later, when you want to find the record of the original position, you can find the position to which it is exchanged in turn.
     

     void Arrange(SLinkListType &SL)
     {
     	p = SL.r[0].next;
     	for(int i=1;i<SL.length;++i)
     	{
     		while(p<i)	p=SL.r[p].next;
     		q = SL.r[p].next;
     		if(p!=i)
     		{
     			Temp(r[p],r[i]);
     			SL.r[i].next = p;
     		}
     		p=q;
     	}//for
     }
     

• algorithm analysis

index	value	analysis
Space complexity S(n)	O(n)	Each record needs another pointer field
Time complexity T(n)	O(n2)	The number of comparisons is the same as that of direct insertion

2.5 Hill sorting

shell sort

void ShellInsert(List &L,int n)//Ascending order
{
	int k=n;
	for(k=n/2;k>=1;k/=2)
	{
		for(int i=k+1;i<n;i++)
		{
			int j=i-k;
			int x=L[i]
			while(j>0&&L[j]>L[i])
			{
				L[j+k]=L[j];
				j-=k;
			}//while
			L[j+k]=x;
		}//For for different elements
	}//for k takes different increments
}//ShellInsert

III Quick sort

Fast classification

A way

int findposition(int l,int r,LIST A)
{
	ELemType p=A[l];
	while(l<r)
	{
		while(l<r&&p<=A[r])	r--;
		if(l<r)
			A[l++]=A[r];
		while(l<r&&p>A[l])	l++;
		if(l<r)
			A[r--]=A[l];
	}
	A[l]=p;
	return l;
}

//Ascending sort

/*Find intermediate value*/
int FindPivot(List &L,int i,int j)//In ascending order, pivot is the first element in the order that is different from the first element and the larger first element
{
	int first=L[i];
	for(int k=i;k<j;k++)
	{
		if(L[k]>first)
			return k;
		else if(L[k]<first)
			return i;
	}//for
	return 0;//The termination condition, i.e. 0 is returned when i==j
}//FindPivot

/*division*/
int Partion(List &L,int i,int j,int pivot)
{
	int L,R,P=L[pivot];
	L=i;
	R=j;
	do
	{
		swap(L[i],L[j]);//For unified operation, exchange first
		while(L[L]<P)
			L+=1;
		while(L[R]>=P)
			R-=1;
	}while(L<=R);
	return L;
}//Partion

/*Fast row, only in line with the division line k, the left side is small, the self and the right side are greater than or equal to pivot, and the pivot is not placed in the correct position*/
void QuickSort(List &L,int i,int j)
{
	int pivot,k;
	pivot=FindPivot(L,i,j);
	if(pivot)//The termination condition is i==j;
	{
		k=Partion(L,i,j,pivot);
		QuickSort(L,i,k-1);
		QuickSort(L,k,j);
	}
}//QuickSort

O (n)=T(nlogn), is the instability classification.
Another kind of fast platoon will select pivot to make it return to the position where it should be, and then recurse on both sides (excluding himself). At this time, it is not exchange, but exchange each other on repeated information until the middle position has been assigned the repeated information as the pivot position without information loss.

IV Select sort

Heap classification

//Sort the heap for a node
void PushDown(int first,int last,List &A)
{
	int r=first;
	while(r<=last/2)
	{
		if(r==last/2 && last%2==0)
		{
			if(A[r]>A[2*r])	swap(A[r],A[2*r]);
			r=last;//End while
		}//If, if there is a node with a degree of one, there is only a left node and no right node to prevent the array from crossing the boundary
		else if(A[r]>A[2*r] && A[2*r]<A[2*r+1])
			swap(A[r],A[2*r]);
		else if(A[r]>A[2*r+1] && A[2*r+1]<A[2*r])
			swap(A[r],A[2*r+1]);
		else
			r=last;//end
	}//while
}//PushDown

void Sort(int n,List &A)
{
	int i,last=n;
	for(i=n/2;i>=1;i--)	PushDown(i,A);//Heap finishing
	for(i=n;i>=2;i--)//Just stay first
		{
			swap(A[1],A[i]);
			PushDown(1,i-1);//The i-th number has been placed as an ordinal number
		}
}//Sort

V Merge sort

Merge classification

//Merge two ordered tables in ascending order
void Merge(int l,int m,int n,List A,List &B)
{
	int i=l,k=l,j=m+1;
	while(i<=m&&j<=n)
	{
		if(A[i]<=A[j])	B[k++]=A[i++];
		else	B[k++]=A[j++];
	}//while
	while(i<=m) T[k++]=A[i++];
	while(j<=n)	T[k++]=A[j++];
}//Merge

//Merge two ordered tables in order of length l
void Mpass(int l,int n,List A,List &B)
{
	int i;
	for(i=1;i<=n-2*l+1;i+=2*l)
	{
		Merge(i,i+l-1,2+2*l-1,A,B);
	}//for two l two traversal merging
	//The rest is dissatisfied with l or 2l
	if(i+l-1<=n)
	{
		Merge(i,i+l-1,n,A,B);
	}
	else
	{
		for(int k=i;k<=n;k++)	B[k]=A[k];
	}
}//Mpass

//Merge from l=1
void M_Sort(int n,List A)
{
	int l=1;
	while(l<n)
	{
		Mpass(l,n,A,B);
		l=2*l;
		Mpass(l,n,B,A);//Attention exchange
		l=2*l;
	}
}

Vi Cardinality classification

Cardinality classification

Applicable to multi keyword classification.

• MSD method: the highest order takes precedence. Heap classification shall be carried out according to the keyword order (from high to low), and then merged.
• LSD method: the lowest priority, starting from the lowest keyword order and sorting from low to high. However, when sorting for a keyword, only stable sorting can be used.

Chain cardinality sort

Sorting for LSD:

• Sort the n records stored in the static linked list
• RADIX linked list queue
• Queue each record into the corresponding queue according to the sequence of keywords from back to front. Then the queue is connected end to end to get the result of sorting a keyword.

VII Comparison of various internal sorting algorithms

6.1 summary

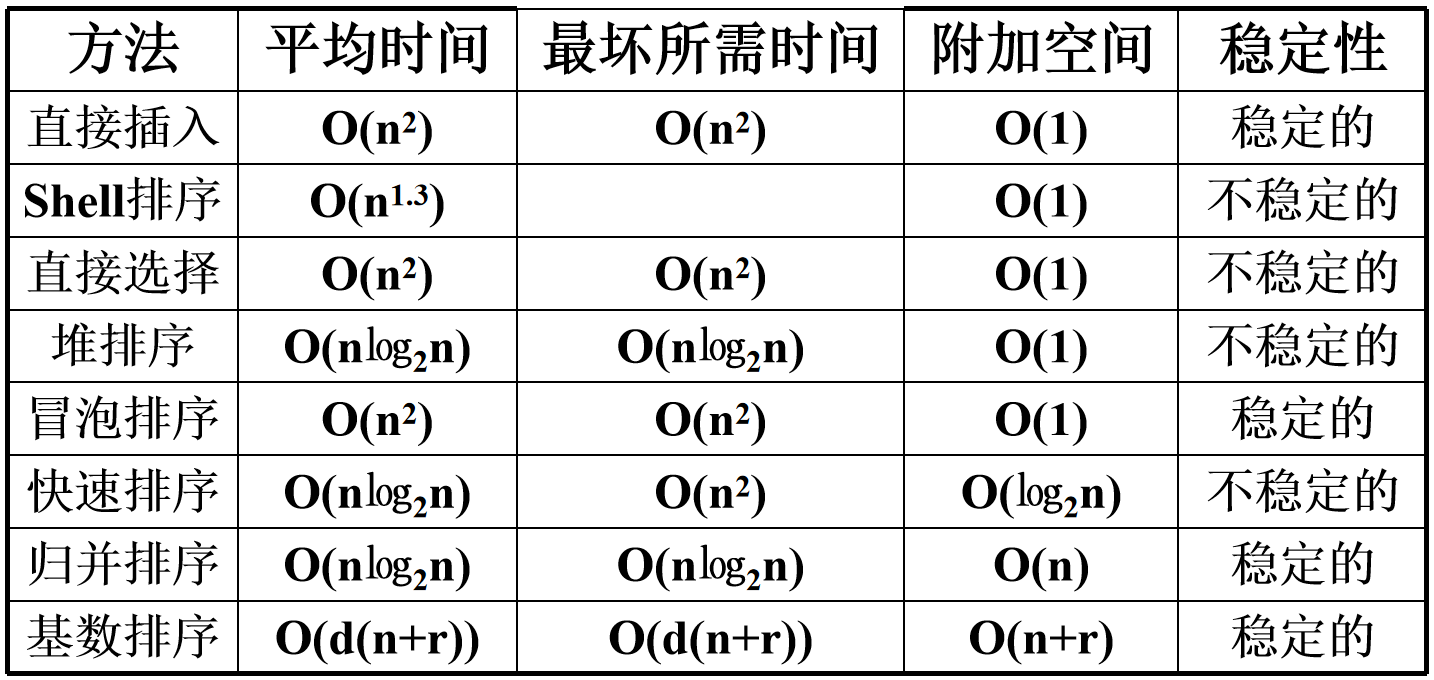
6.2 description

1. Simple sorting (direct insertion, direct selection, bubble sorting)
   Both are nested in two layers of loops.
   Stability:
   Direct insertion: when the insertion condition is "strictly less than / greater than a value, insert in front of the value", it can ensure stability.
   Direct selection: because the front will be replaced by the back in the selection process, it is unstable.
   Bubble sort: obviously.
2. shell sort
   The time performance of hill sorting is between O(nlogn) and O(n2). When n is in a specific range, it is N1 3.
   Stability: obviously unstable.
3. Heap sort
   First, initialize the heap building and push down n/2 data. The worst case of each push down is the layer height of the complete binary tree, that is, log (n+1), and the time complexity is (n/2) * (log (n+1)); Then take the top of the stack as the arrangement, and the operation time complexity is (n/2) (log (n+1)) Therefore, the complexity is O(nlogn)
   Stability: unstable.
4. Quick sort
   If each time is exactly the midpoint of the sequence, it is a sort in the form of binary tree, and the time complexity is O (nlogn). If it is head / tail each time, it degenerates into selective sorting, O(n2)
   Each fast row requires two pointer bits and one pivot value temporary storage bit, a total of logn times. So it is O(logn).
   Stability: unstable.
5. Merge sort
   Each time, n elements are operated, and a total of n operations are performed (binary tree layer height), so it is (n logn).
   The auxiliary space O (n) is required as the merged storage space. (the two spaces fall back and forth).
   As long as the order of merging is determined to be left first and then right, the sequence of elements with the same size can be maintained all the time.
6. Cardinality sort
   There are d keywords and n records in total, and the value range of each record is r. Then LSD method will execute D times for D keywords from the lowest point. Each time, it is necessary to put n elements into the corresponding queue, and then connect the end of R queues to R, then the time complexity is O (d (n+r))
   Auxiliary space required: n pointer fields, 2r queue pointer fields, i.e. O(n+r);
   Obviously stable.

6.3 sorting performance test data

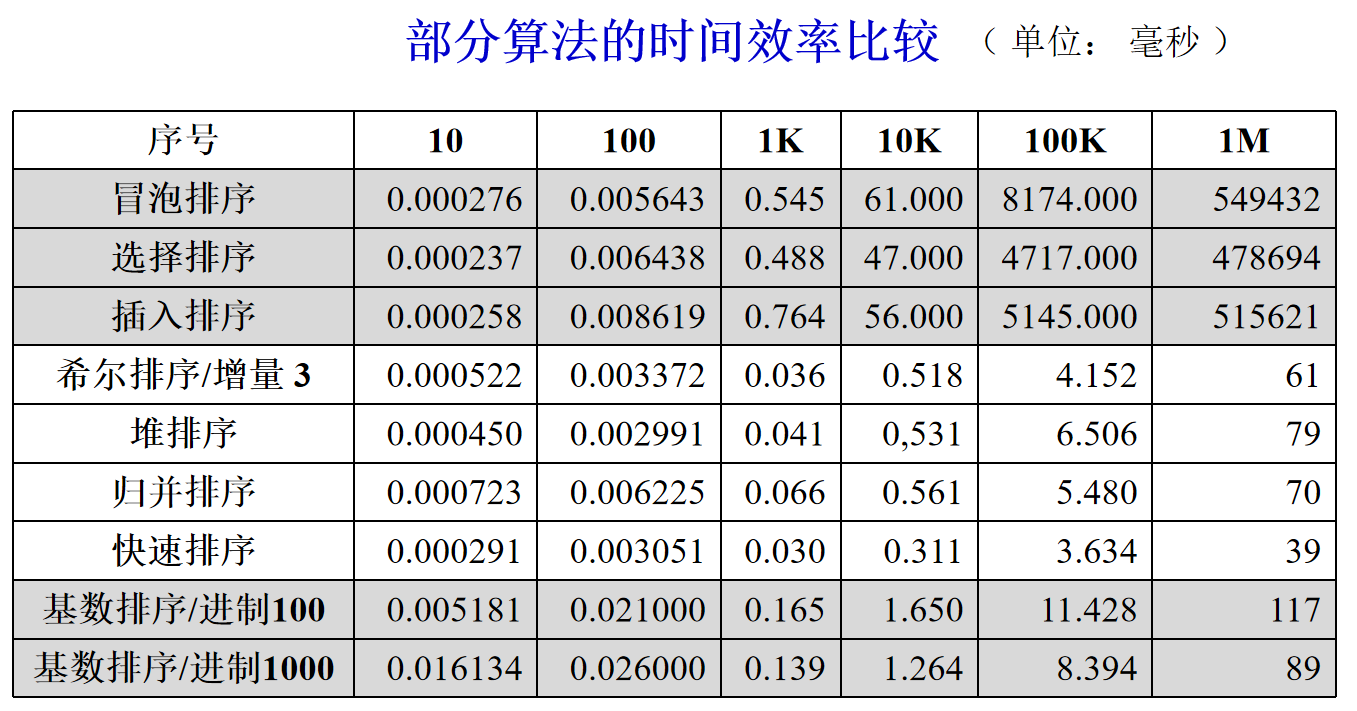
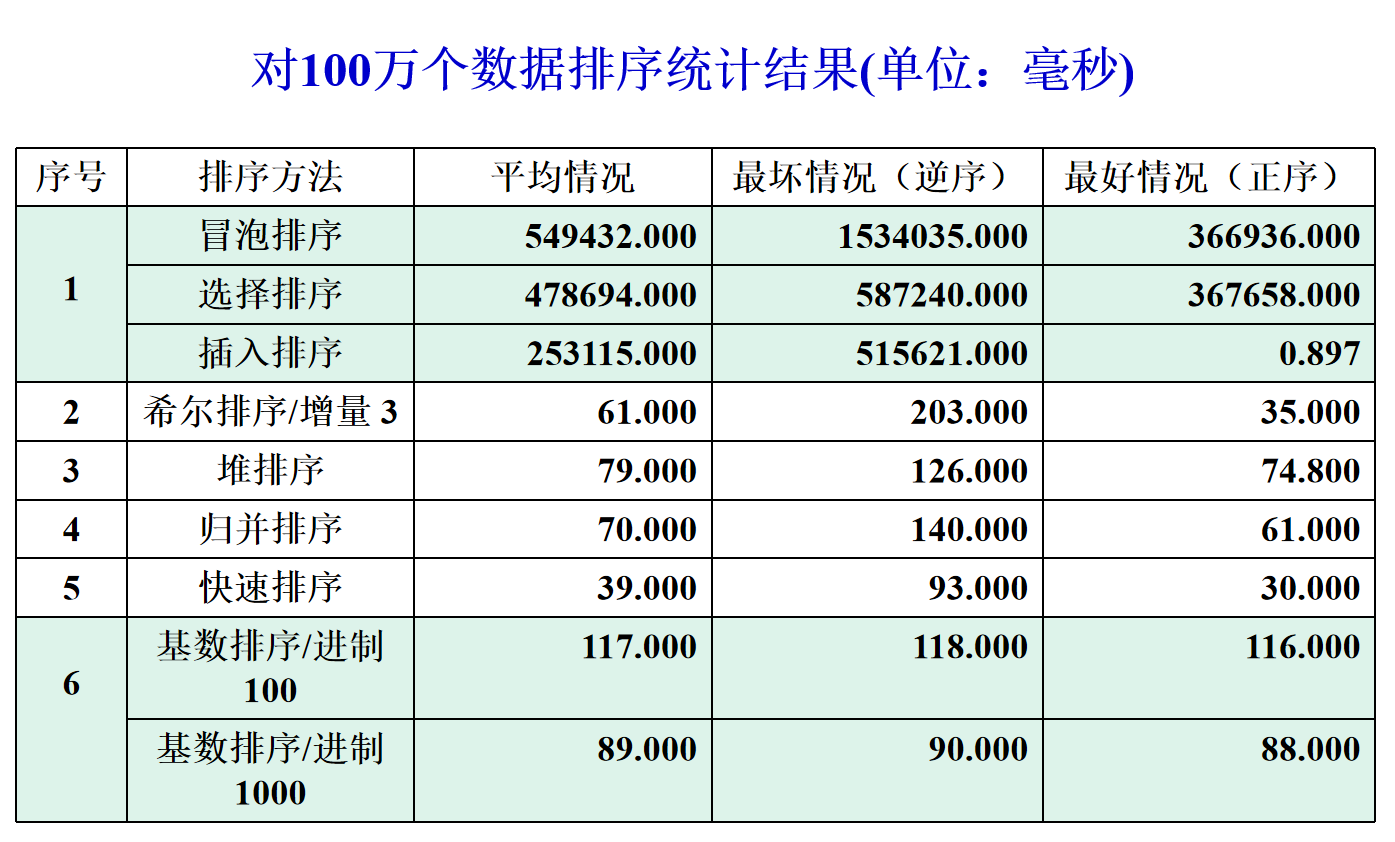
6.4 select different sorting methods under different conditions