Chain List Introduction
1.1 Comparison of advantages and disadvantages between order table and chain table
Sequence table
Advantages: Any element in the table can be accessed at any time;
Disadvantages: Insert and delete operations require a large number of elements to be moved.
Chain Storage Linear Table
Advantages: No storage unit with contiguous addresses is required, and insertion and deletion operations do not require moving elements, only modifying the pointer;
Disadvantages: Loss of the advantage of random access to sequential tables.
Singly Linked List
Advantages: Solve the disadvantage that sequential tables require a large number of continuous storage units;
Disadvantages: Single-chain lists add pointer fields, which wastes storage space. When looking for a specific node, it is necessary to traverse from the header and look for it in turn.
1.2 Single Chain Table Definition
The chain storage of a linear table is called a single-chain table, which consists of a data field and a pointer field, which stores data elements, and a pointer field which stores the addresses of its subsequent nodes.
Single-chain table implementation:
Unheaded Node-->Empty Table Judgment: L=== NULL. Code writing is inconvenient
Leading Node-->Empty Table Judgment: L-> next==NULL. Writing code is more convenient (this is generally recommended)
Single Chain List Node Type Code Description:
typedef struct LNode {
int data; // Node Data Domain
struct LNode *next; // Pointer Domain of Node
} LNode, *LinkList; // LinkList is a pointer type to struct LNode
"LinkList" is "equivalent to" LNode. The former emphasizes that this is a chain list, the latter emphasizes that this is a node, the appropriate place to use the appropriate name, and the code is more readable.
2. Basic operation of single-chain list
2.1 Bitwise insertion (leading node postinsertion)
ListInsert (&L, i, e): Insert operation. Insert the specified element E at the ith position i n table L. Average time complexity O(n)
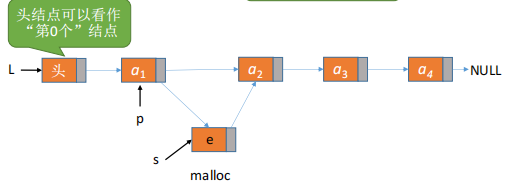
[Analysis]: 1. Define the chain table structure first; 2. In the algorithm, determine if I position i s <1, create pointer *p pointing to the head node, find the i-1 node in the loop *p, insert it; 3. Create a node s to store element e, the next position of p i s the next position of s, that I s, assign p to s:s->next=p->next; and then the next position that becomes p i s s, that I s, p->next=s.
typedef struct LNode {
ElemType data; // Node Data Domain
struct LNode *next; // Pointer Domain of Node
} LNode, *LinkList; // LinkList is a pointer type to struct LNode
//Insert specified element e at position i I
bool ListInsert(LinkList &L, int i, ElemType e){
if(i<1)
return false;
LNode *p; // Pointer p points to the currently scanned node
int j=0; // The current p is pointing to the number of nodes
p =L; // L points to the head node, which is the 0th node (there is no data)
while (p!=NULL && j<i-1) { //Loop to find node 1-1
p=p->next;
j++;
}
if(p==NULL) // Illegal i value
return false;
LNode *s = (LNode*)malloc(sizeof(LNode));
s->data = e;
s->next=p->next;
p->next=s; // Connect node s after p
return true; // Insert Successful
}
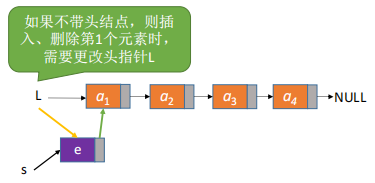
Without the post-interpolation of the first node, the operation at the first node is different from that of the other nodes.
[Analysis]: 1, Create new node *s, 2, s data field is element e, s next is L itself; 3, then s will become the original L.
if(i==1){ // Insert the first node differently from the other nodes
LNode *s = (LNode*)malloc(sizeof(LNode));
s->data = e;
S->next=L ;
L=s; //Head Pointer Points to New Node
return true;
}
2.2 Interpolation operations for specified nodes
//Post-insert operation: insert element e after p-node
bool InsertNextNode (LNode *p, ElemType e){
if (p==NULL)
return false;
LNode *s = (LNode *)malloc(sizeof(LNode));
if (s==NULL) //memory allocation failed
return false;
s->data = e; //Save data element e with node s
s->next=p->next;
p->next=s; //Connect node s after p
return true;
}
call:return InsertNextNode(p,e)
2.3 Front Interpolation of Specified Nodes
Pre-insert operation: insert element e before the p-node.
How do I find the precursor of a p-node?
[Analysis 1]: With a known p node, the head pointer L can be passed in, the precursor Q of p can be looped, and then q can be interpolated back to complete the algorithm operation. Time complexity O(n).
[Analysis 2]: Known P node, create s node, we think that if the element value of P is e and the element value of S is p, then it can be a forward interpolation operation!!
- Next of s = next of p;
- next=s for p;
- Data of s = data of p;
- The data for p is e.
// Pre-insert operation: insert element e before the p-node.
bool InsertPriorNode (LNode *p, ElemType e){
if (p==NULL)
return false;
LNode *s = (LNode *)malloc(sizeof(LNode));
if (s==NULL) //memory allocation failed
return false;
s->next=p->next;
p->next=s; //Connect node s after p
s->data=p->data
p->data=e; // Elements in p are covered by e
return true;
}
2.4 Bitwise deletion (leading node)
ListDelete (&L, i, &e): Delete operation. Delete the element of the ith node i n table L and return the value of the deleted element with E. Time complexity O(n)
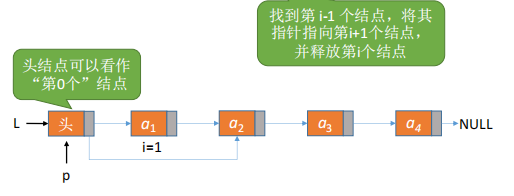
[Analysis]: Similar to insertion of 2.1, except the core code is different. Check the legality of the location of the deleted node, find the i-1 node*p, and then say that the pointer field of *p points to the next node of the deleted node*q, and release *q.
if(p==NULL) // Illegal i value
return false;
if(p->next == NULL) // Node i I has no
return false;
LNode *q=p->next; // Make q point to deleted node
e = q->data; // Return the value of an element with e
p->next=q->next; // Break *q Node from Chain
free(q); // Release storage space for nodes
return true; // Delete succeeded
2.5 Deletion of specified node p
[Analysis]: To delete the p-node, the precursor of P is unknown and the subsequent q is available. Then P exchanges the data domain with the next of p, assigns the next of Q to the next of p, and finally releases Q. Time complexity O(1)
//Delete the specified node p
bool DeleteNode (LNode *p){
if (p==NULL)
return false;
LNode *q=p->next; // Point q to the next node of *p
p->data=p->next->data; // Exchange data fields with subsequent nodes
p->next=q->next; // Break *q Node from Chain
free(q); // Release storage space for subsequent nodes
return true;
}
[Note) When specifying a node is the last node, special handling is required
2.6 Find values by location
Bitwise lookup returns the first element (leading node)
[Analysis]: 1. Judge the legal location of i, create node *p pointing to head node L; 2, while loop finds the ith node, and finally return p. Time complexity O(n)
Starting from the first node in the single-chain list, search down the next pointer field one by one until the ith node is found, otherwise return to the last pointer field NULL.
// Bitwise lookup returns the first element (leading node)
LNode *GetElem(LinkList L, int i){
if(i<0 )
return NULL;
LNode *p; //Pointer p points to the currently scanned node
int j=0; //The current p is pointing to the number of nodes
p=L; //L points to the head node, which is the 0th node (there is no data)
while (p!=NULL && j<i) { //Loop to find the ith node
p=p->next;
j++;
}
return p;
}
2.7 Find Table Nodes by Value
Starting from the first node of a single-chain table, the values of each node's data field in the table are compared one after the other. If the value of a node's data field equals the given value e, a pointer to the node is returned: if there is no such node in the entire single-chain table, NULL is returned with time complexity O(n).
LNode *LocateElem (LinkList L, ElemType e) {
LNode *p=L->next;
while (p!=NULL&&p->data!=e) // Find nodes with data field e starting from the first node
p-p->next;
return P; // Return the node pointer when found, otherwise return NULL
}