Binary tree
1. Tree structure
1.1 concept
Tree is a nonlinear data structure. It is a set with hierarchical relationship composed of n (n > = 0) finite nodes. It is called a tree because it looks like an upside down tree, that is, it has roots up and leaves down. It has the following characteristics:
- There is a special node, called the root node, which has no precursor node
- Except for the root node, the other nodes are divided into m (M > 0) disjoint sets T1, T2,... Tm, in which each set Ti (1 < = I < = m) is a subtree similar to the tree. The root node of each subtree has only one precursor, and can have 0 or more successors
- Trees are recursively defined.


Node degree: the number of subtrees contained in a node is called the degree of the node; As shown in the figure above: A is 6
Tree degree: the degree of the largest node in a tree is called the degree of the tree; As shown in the figure above: the degree of the tree is 6
Leaf node or terminal node: a node with a degree of 0 is called a leaf node; As shown in the figure above, nodes B, C, H, I... Are leaf nodes
Parent node or parent node: if A node contains child nodes, this node is called the parent node of its child nodes; As shown in the figure above, A is the parent node of B
Child node or child node: the root node of the subtree contained in a node is called the child node of the node; As shown in the figure above: B is the child node of A
Root node: A node in A tree without parent nodes; As shown in the figure above: A
Node hierarchy: defined from the root, the root is the first layer, and the child node of the root is the second layer, and so on;
Height or depth of tree: the maximum level of nodes in the tree; As shown in the figure above: the height of the tree is 4
Non terminal node or branch node: a node whose degree is not 0; As shown in the figure above, nodes D, E, F, G... Are branch nodes
Sibling node: nodes with the same parent node are called sibling nodes; As shown in the figure above, B and C are sibling nodes
Cousin node: nodes with parents on the same layer are cousins to each other; As shown in the figure above, H and I are brother nodes to each other
Ancestor of a node: all nodes from the root to the branch through which the node passes; As shown in the figure above: A is the ancestor of all nodes
Descendant: any node in the subtree with a node as the root is called the descendant of the node. As shown in the figure above: all nodes are descendants of A
Forest: a collection of m (m > = 0) disjoint trees is called forest
1.2 representation of tree
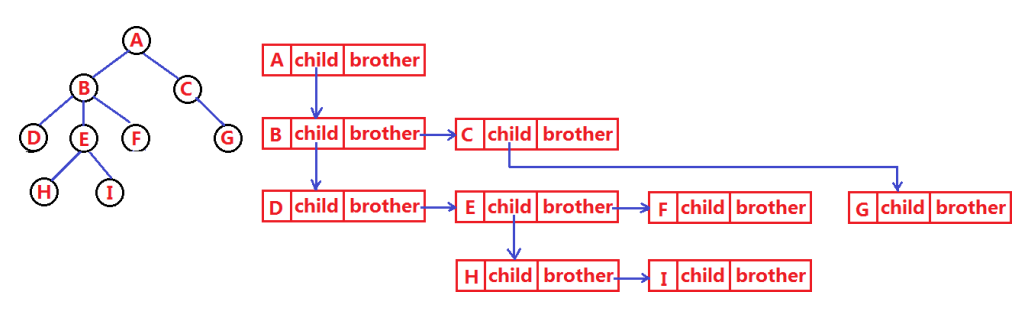
The tree structure is more complex than the linear table, and it is more troublesome to store and express. In fact, there are many kinds of tree representations, such as parent representation, child representation, child brother representation and so on. Let's simply understand the most commonly used child brother expression.
class Node {
int value;// Data stored in the tree
Node firstChild;// First child quote
Node nextBrother;// Next brother reference
}
1.3 application of tree
File system management (directories and files)

2. Binary tree
2.1 concept
A binary tree is a finite set of nodes, which is either empty, or a root node plus two binary trees called left subtree and right subtree
Tree composition.
Characteristics of binary tree:
1. Each node has at most two subtrees, that is, the binary tree does not have nodes with a degree greater than 2.
2. The subtree of a binary tree can be divided into left and right, and the order of its subtrees cannot be reversed. Therefore, a binary tree is an ordered tree.
2.2 basic form of binary tree
Generally, binary trees are formed by the combination of the following basic forms.

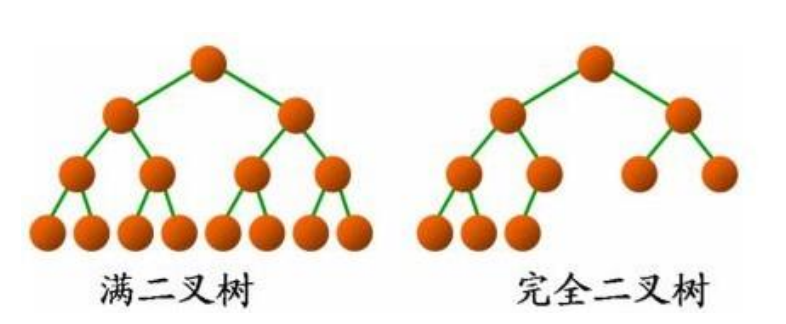
2.3 two special binary trees
- Full binary tree: a binary tree. If the number of nodes in each layer reaches the maximum, the binary tree is a full binary tree. In other words, if the number of layers of a binary tree is K and the total number of nodes is, it is a full binary tree.
- Complete binary tree: a complete binary tree is a highly efficient data structure. A complete binary tree is derived from a full binary tree. A binary tree with depth K and n nodes is called a complete binary tree if and only if each node corresponds to the nodes numbered from 1 to n in the full binary tree with depth K. It should be noted that full binary tree is a special complete binary tree.
2.4 properties of binary tree
- If the number of layers of the root node is specified as 1, there are at most 2i-1 (I > 0) nodes on layer I of a non empty binary tree
- If the depth of the binary tree with only the root node is specified as 1, the maximum number of nodes of the binary tree with depth K is 2k-1 (k > = 0)
- For any binary tree, if the number of leaf nodes is n0 and the number of non leaf nodes with degree 2 is n2, then n0 = n2 + 1
- The depth k of a complete binary tree with n nodes is rounded on log2(n+1)
- For a complete binary tree with n nodes, if all nodes are numbered from 0 from top to bottom and from left to right, the nodes with sequence number i are:
If I > 0, parental serial number: (i-1)/2; i=0, I is the root node number, no parent node
If 2i+1 < n, left child serial number: 2i+1, otherwise there is no left child
If 2i+2 < n, right child serial number: 2i+2, otherwise there is no right child
For example, if there are 1000 nodes in a complete binary tree, there are 500 leaf nodes and 500 non leaf nodes in the binary tree. One node has only left children and 0 has only right children.
2.5 storage of binary tree
The storage structure of binary tree is divided into sequential storage and chain storage similar to linked list.
Sequential storage is a complete binary tree
The chained storage of binary tree is referenced by nodes one by one. The common representations include binary and trigeminal representations, as follows:
// Child representation
class Node {
int val;// Data domain
Node left;// The reference of the left child often represents the whole left subtree with the left child as the root
Node right; // The reference of the right child often represents the whole right subtree with the right child as the root
}
// Child parent representation
class Node {
int val;// Data domain
Node left;// The reference of the left child often represents the whole left subtree with the left child as the root
Node right; // The reference of the right child often represents the whole right subtree with the right child as the root
Node parent; // The root node of the current node
}
2.6 traversal of binary tree
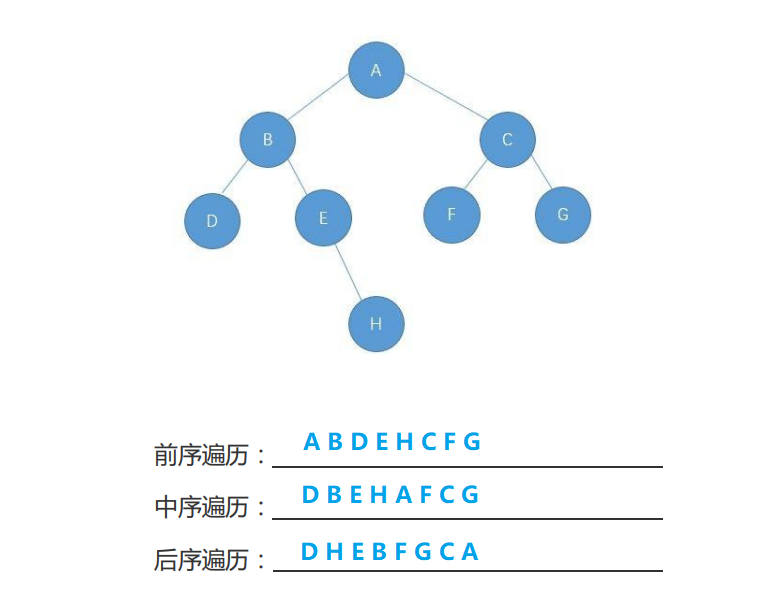
If N represents the root node, L represents the left subtree of the root node, and R represents the right subtree of the root node, there are the following traversal methods according to the order of traversing the root node:
- NLR: Preorder Traversal (also known as Preorder Traversal) - access the root node - > the left subtree of the root - > the right subtree of the root.
- LNR: inorder traversal - left subtree of root - > root node - > right subtree of root.
- LRN: postorder traversal - left subtree of root - > right subtree of root - > root node.

2.7 basic operation of binary tree
Step 1: first, we use the exhaustive method to create a binary tree to test these operations
package BinaryTree;
class TreeNode{
public char val;
public TreeNode left;
public TreeNode right;
public TreeNode(char val){
this.val = val;
}
}
public class BinaryTree {
public TreeNode createTree() {
TreeNode A = new TreeNode('A');
TreeNode B = new TreeNode('B');
TreeNode C = new TreeNode('C');
TreeNode D = new TreeNode('D');
TreeNode E = new TreeNode('E');
TreeNode F = new TreeNode('F');
TreeNode G = new TreeNode('G');
TreeNode H = new TreeNode('H');
A.left = B;
A.right = C;
B.left = D;
B.right = E;
E.right = H;
C.left = F;
C.right = G;
return A;
}
}
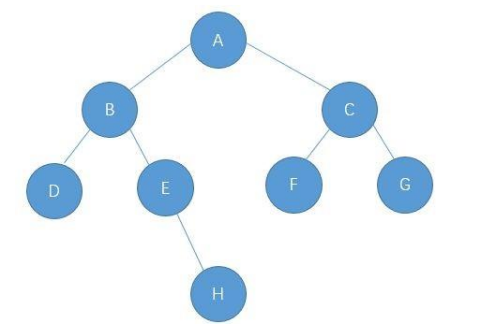
The binary tree graph is shown as follows:
Step 2: implement three methods of traversing binary tree with code
// Preorder traversal
void preOrderTraversal(TreeNode root) {
if (root == null) {
return;
}
System.out.print(root.val + " ");
preOrderTraversal(root.left);
preOrderTraversal(root.right);
}
// Medium order traversal
void inOrderTraversal(TreeNode root){
if(root == null){
return;
}
inOrderTraversal(root.left);
System.out.print(root.val + " ");
inOrderTraversal(root.right);
}
// Postorder traversal
void postOrderTraversal(TreeNode root){
if(root == null){
return;
}
postOrderTraversal(root.left);
postOrderTraversal(root.right);
System.out.print(root.val + " ");
}
Step 3: find the number of nodes by two methods
// Traversal idea - find the number of nodes
static int size = 0;
void getSize1(TreeNode root){
if(root == null){
return;
}
size++;
getSize1(root.left);
getSize1(root.right);
}
// Idea of subproblem - finding the number of nodes
int getSize2(TreeNode root){
if(root == null){
return 0;
}
return getSize2(root.left) + getSize2(root.right) + 1;
}
Step 4: find the number of leaf nodes by two methods
// Traversal idea - find the number of leaf nodes
static int leafSize = 0;
void getLeafSize1(TreeNode root){
if(root == null){
return ;
}
if(root.left == null && root.right==null){
leafSize++;
}
getLeafSize1(root.left);
getLeafSize1(root.right);
}
// Idea of subproblem - finding the number of leaf nodes
int getLeafSize2(TreeNode root){
if(root == null){
return 0;
}
if(root.left == null && root.right ==null){
return 1;
}
return getLeafSize2(root.left) + getLeafSize2(root.right);
}
Step 5: find the number of nodes in layer k
int getKLevelSize(TreeNode root,int k){
if(root == null){
return 0;
}
if(k == 1){
return 1;
}
return getKLevelSize(root.left,k-1) + getKLevelSize(root.right,k-1) ;
}
Step 6: find the location of val
// Find the node where val is located. If it is not found, null will be returned
// Search in the order of root - > left subtree - > right subtree
// Once found, return immediately. There is no need to continue searching in other locations
TreeNode find(TreeNode root, char val){
if(root == null){
return null;
}
if(root.val == val){
return root;
}
TreeNode ret = find(root.left,val);
if(ret != null){
return ret;
}
ret = find(root.right,val);
if(ret != null){
return ret;
}
return null;
}
Step 7: get the height of the binary tree
// Gets the height of the binary tree
int getHeight(TreeNode root){
if(root == null){
return 0;
}
int leftHeight = getHeight(root.left);
int rightHeight = getHeight(root.right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
Step 8: run the test results
public static void main(String[] args) {
BinaryTree binaryTree = new BinaryTree();
TreeNode root = binaryTree.createTree();
System.out.print("Preorder traversal result: ");
binaryTree.preOrderTraversal(root);
System.out.println();
System.out.print("Middle order traversal result: ");
binaryTree.inOrderTraversal(root);
System.out.println();
System.out.print("Postorder traversal result: ");
binaryTree.postOrderTraversal(root);
System.out.println();
binaryTree.getSize1(root);
System.out.println("Node number: "+BinaryTree.size);
int ret = binaryTree.getSize2(root);
System.out.println("Node number: "+ret);
binaryTree.getLeafSize1(root);
System.out.println("Number of leaf nodes: "+BinaryTree.leafSize);
int ret1 = binaryTree.getLeafSize2(root);
System.out.println("Number of leaf nodes: "+ret1);
int ret2 = binaryTree.getKLevelSize(root,3);
System.out.println("seek k Number of layer nodes: "+ret2);
TreeNode b= binaryTree.find(root,'H');
System.out.println(b.val);
System.out.println("Find the depth of binary tree: "+binaryTree.getHeight(root));
}
Operation results:

2.8 sequence traversal
Let the number of layers of the root node of the binary tree be 1. Sequence traversal is to start from the root node of the binary tree, first access the root node of the first layer, then access the nodes on the second layer from left to right, then the nodes on the third layer, and so on. The process of accessing the nodes of the tree layer by layer from top to bottom and from left to right is sequence traversal.


a) Code implementation:
// level traversal
void levelOrderTraversal(TreeNode root){
if(root == null) return ;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
TreeNode top = queue.poll();
System.out.print(top.val+" ");
if(top.left != null)
queue.offer(top.left);
if(top.right != null)
queue.offer(top.right);
}
System.out.println();
}
b) Judge whether a tree is a complete binary tree
Method 1 idea:
1. Put the tree into the queue according to the sequence traversal method. The difference is that the left and right nodes are put into the queue, regardless of whether the node is empty or not
2. The loop takes out the queue head element. If the queue head is null, the loop ends
3. If the queue is not empty at this time
① If there are nodes in the queue, it is not a complete binary tree
② If the queue is all null, it is a complete binary tree
4. If the loop ends, it is true;
Code implementation:
boolean isCompleteTree(TreeNode root) {
if (root == null) return true;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode top = queue.poll();
//Both the left and right subtrees are queued (whether null or not)
if (top != null) {
queue.offer(top.left);
queue.offer(top.right);
} else {
//If the head of the team is empty, jump out of the loop
break;
}
}
//If the queue is not empty, it indicates that it is because of the cycle ended by break Then you need to judge the elements in the team
while (!queue.isEmpty()) {
TreeNode cur = queue.peek();
//If the head of the team is empty, get out of the team
if (cur == null){
queue.poll();
}else {
//If you encounter a node that is not empty, it means that it is not a complete binary tree
return false;
}
}
//If the queue is empty, it is true;
return true;
}
Method 2 idea:
1. Looking at the graph of a complete binary tree, we can see that each node has either two child nodes, or no nodes, or only one left node and no right node
2. Traversal judgment
① If the left and right subtrees are not empty, join the team
② If the left subtree exists and the right subtree does not exist, the second judgment is made
③ If the left subtree does not exist and the right subtree does not exist, then it is directly false
④ If the left subtree and the right subtree do not exist, the second judgment is also entered
3. The second judgment is to judge whether the next left subtree and right subtree are empty. If not, it is false; Always empty is true;
Code implementation:
boolean isCompleteTree1(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
boolean isComplete = true;
while(!queue.isEmpty()){
TreeNode top = queue.poll();
if(isComplete) {
//1. Do not join the team empty
if (top.left != null && top.right != null) {
queue.offer(top.left);
queue.offer(top.right);
} else if (top.left != null && top.right == null) {
//2. If the left subtree is not empty and the right subtree is empty, enter the second judgment
isComplete = false;
queue.offer(top.left);
} else if (top.left == null && top.right != null) {
//3. The left subtree is empty and the right subtree is not empty, which does not conform to the concept of complete binary tree. false
return false;
} else {
//4. If the left and right subtrees are empty, enter the second judgment
isComplete = false;
}
}else {
//Second judgment
//If the following nodes have subtrees, it does not conform to the concept of complete binary tree. false
if(top.left != null || top.right != null){
return false;
}
}
}
//When the loop traversal ends, the condition is met and true is returned;
return true;
}
2.9 non recursive implementation of pre middle post sequence
① Preorder traversal (non recursive)
// Preorder traversal
void preOrderTraversal(TreeNode root) {
if (root == null) return;
TreeNode cur = root;
Stack<TreeNode> stack = new Stack<>();
while (cur != null || !stack.empty()) {
while (cur != null) {
stack.push(cur);
System.out.print(cur.val+" ");
cur = cur.left;
}
TreeNode top = stack.pop();
cur = top.right;
}
}
② Medium order traversal (non recursive)
// Medium order traversal
void inOrderTraversal(TreeNode root){
if(root == null) return ;
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while(cur != null || !stack.empty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
TreeNode top = stack.pop();
System.out.print(top.val + " ");
cur = top.right;
}
}
③ Postorder traversal (non recursive)
// Postorder traversal
void postOrderTraversal(TreeNode root){
if(root == null)
return;
TreeNode cur = root;
TreeNode pre = null;//Used to point to the last printed element
Stack<TreeNode> stack = new Stack<>();
while(cur != null || !stack.empty()){
while(cur != null){
stack.push(cur);
cur = cur.left;
}
cur = stack.peek();
if(cur.right == null || pre == cur.right ){
stack.pop();
System.out.print(cur.val+" ");
pre = cur;
cur = null;
}else {
cur = cur.right;
}
}
}