1, Binary tree
Binary tree is the same dynamic data structure as linked list. Binary tree has natural recursive structure, that is, the left subtree of each node is also a binary tree, and the right subtree of each node is also a binary tree.
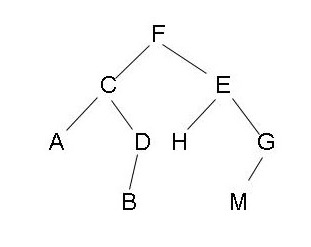
2, Binary search tree
2.1 features
Our binary search tree does not contain duplicate elements. If you want to include duplicate elements, you only need to define: the left subtree is less than or equal to nodes, and the right subtree is greater than or equal to nodes.
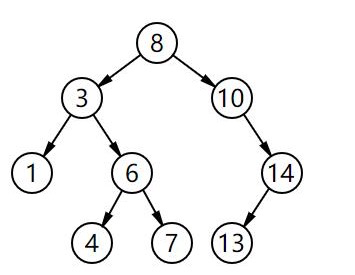
Implementation of binary search tree:
1. Add binary search tree:
Use the recursive algorithm to insert elements into the binary search tree with node as the root. The recursive algorithm compares nodes. If it is larger than the value of the node, it will be inserted into the right subtree. If it is smaller, it will be inserted into the left subtree.
2. Check whether the binary search tree contains elements:
Using recursive algorithm, if it is smaller than the node, it will recurse the left subtree, and if it is larger than the node, it will recurse the right subtree.
3. Traversal of binary search prime tree:
Traversal is divided into: pre sequence traversal, middle sequence traversal, post sequence traversal and sequence traversal.
DLR - preorder traversal (root first, from left to right, the root of a tree is always in front of the left subtree, and the left subtree is always in front of the right subtree)
LDR – medium order traversal (the root is in the middle, from left to right, the left subtree of a tree is always in front of the root, and the root is always in front of the right subtree)
LRD - post order traversal (the root is behind, from left to right, the left subtree of a tree is always in front of the right subtree, and the right subtree is always in front of the root)
4. Delete node
Delete nodes are divided into three categories: delete the smallest node, delete the largest node and delete the intermediate node.
Delete minimum node:
First, find the minimum node element to see if the node has a right subtree, and point the left subtree of the parent node to the right subtree of the node.
Delete maximum node:
First find out the maximum node element to see if the node has a left subtree, and point the right subtree of the parent node to the left subtree of the node.
Delete intermediate node:
1. Check whether the node has left subtree and no right subtree. If so, point the parent node to the left subtree
2. Check whether the node has a right subtree and no left subtree. If so, point the parent node to the right subtree
3. If there is a left subtree and a right subtree, calculate the minimum value node of the right subtree. The left subtree of the minimum value node is the left subtree of the deleted node, and the right subtree is the right subtree after the deleted minimum value node.
2.2 specific code implementation of binary search prime tree
Through the introduction of 2.1, the specific code implementation contents are as follows:
public class BST<E extends Comparable<E>> {
private class Node{
public E e;
public Node left, right;
public Node(E e){
this.e = e;
left = null;
right = null;
}
}
private Node root;
private int size;
public BST(){
root = null;
size = 0;
}
public int size(){
return this.size;
}
public boolean isEmpty(){
return this.size == 0;
}
//Add a new element to the binary search tree e
public void add(E e){
root = addNode(root,e);
}
//Insert element E into the binary search tree with node as the root, recursive algorithm
//Returns the root of the binary search tree after inserting a new node
private Node addNode(Node node, E e){
if(node == null){
size++;
return new Node(e);
}
if(e.compareTo(node.e) < 0)
node.left = addNode(node.left,e);
else if (e.compareTo(node.e) > 0)
node.right = addNode(node.right,e);
return node;
}
//See if the binary search tree contains the element e
public boolean contains(E e){
return contains(root, e);
}
private boolean contains(Node node, E e){
if(node == null)
return false;
if(e.compareTo(node.e) == 0)
return true;
else if(e.compareTo(node.e) < 0)
return contains(node.left, e);
else //e.compareTo(node.e)>0
return contains(node.right, e);
}
//Preorder traversal of binary search tree
public void preOrder(){
preOrder(root);
}
//The preamble traverses the binary search tree with node as the root, and the recursive algorithm
private void preOrder(Node node){
if (node == null)
return;
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
//Non recursive traversal of binary search tree
public void preOrderNR(){
Stack<Node> stack = new ArrayStack<>();
stack.push(root);
while (!stack.isEmpty()){
Node cur = stack.pop();
System.out.println(cur.e);
if (cur.right != null)
stack.push(cur.right);
if (cur.left != null)
stack.push(cur.left);
}
}
public void inOrder(){
inOrder(root);
}
//In order to traverse the binary search tree with node as the root, recursive algorithm
public void inOrder(Node node){
if(node == null)
return;
inOrder(node.left);
System.out.println(node.e);
inOrder(node.right);
}
//Post order traversal of binary search tree
public void postOrder(){
postOrder(root);
}
//After traversing the binary search tree with node as the root, recursive algorithm
public void postOrder(Node node){
if(node == null)
return;
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
}
//Sequence traversal of binary search tree
public void levelOrder(){
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
Node cur = queue.remove();
System.out.println(cur.e);
if(cur.left != null)
queue.add(cur.left);
if (cur.right != null)
queue.add(cur.right);
}
}
//Find the smallest element of binary search tree
public E minimum(){
if(size == 0)
throw new IllegalArgumentException("BST is empty!");
return minimum(root).e;
}
//Returns the node where the minimum value of the binary search tree with node as the root is located
private Node minimum(Node node){
if (node.left == null)
return node;
return minimum(node.left);
}
//Find the largest element of the binary search tree
public E maximum(){
if(size == 0)
throw new IllegalArgumentException("BST is empty!");
return maximum(root).e;
}
//Returns the node where the minimum value of the binary search tree with node as the root is located
private Node maximum(Node node){
if (node.right == null)
return node;
return maximum(node.right);
}
//Delete the node with the minimum value from the binary search tree and return the minimum value
public E removeMin(){
E ret = minimum();
root = removeMin(root);
return ret;
}
//Delete the smallest node in the binary search tree with node as the root
//Returns the root of the new binary search tree after deleting the node
private Node removeMin(Node node){
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
//Delete the node with the maximum value from the binary search tree and return the maximum value
public E removeMax(){
E ret = maximum();
root = removeMax(root);
return ret;
}
//Delete the largest node in the binary search tree with node as the root
//Returns the root of the new binary search tree after deleting the node
private Node removeMax(Node node){
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
//Delete the node with element e from the binary search tree
public void remove(E e){
remove(root, e);
}
//Delete the node with the value of e in the binary search tree with node as the root, and use the recursive algorithm
//Returns the root of the new binary search tree after deleting the node
private Node remove(Node node, E e){
if(node == null)
return null;
if(e.compareTo(node.e) < 0){
node.left = remove(node.left, e);
return node;
}
else if(e.compareTo(node.e) > 0){
node.right = remove(node.right, e);
return node;
}
else{ //e == node.e
//The left subtree of the deleted node is empty
if (node.left == null){
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
//The right subtree of the deleted node is empty
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
//The left and right subtrees of the deleted node are not empty
//Find the smallest node than the node to be deleted, that is, the smallest node of the right subtree of the node to be deleted
//Replace the position of the node to be deleted with this node
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
generateBSTString(root, 0, res);
return res.toString();
}
//Generate a string describing the binary tree with node as the root node and depth as depth
private void generateBSTString(Node node, int depth, StringBuilder res){
if(node == null){
res.append(generateDepthString(depth) + "null\n");
return;
}
res.append(generateDepthString(depth) + node.e + "\n");
generateBSTString(node.left, depth + 1, res);
generateBSTString(node.right, depth+ 1, res);
}
private String generateDepthString(int depth){
StringBuilder res= new StringBuilder();
for (int i = 0; i < depth; i++) {
res.append("--");
}
return res.toString();
}
}