What is a complete binary tree

Complete binary tree

Method 1

Depth first search, first search the left subtree, then the right subtree. When the traversing node is a leaf node, the depth of the leaf node is stored in the array, and finally judge whether the number is like a shape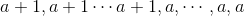Or like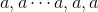If so, then this tree is a complete binary tree, otherwise, it is not a complete binary tree. Take the following tree as an example. The code is as follows:

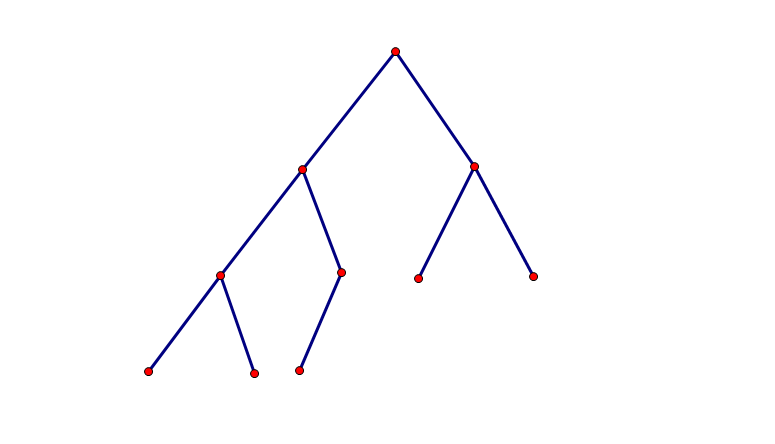
#include <bits/stdc++.h>
#define ll long long
using namespace std;
struct node
{
	node* left;
	node* right;
}*tree[1005], *root;
int deep[1005], cnt;
//Initialize tree building
void Init()
{
	for (int i = 0; i < 1005; i++)
	{
		tree[i] = (node*)malloc(sizeof(node));
		tree[i]->left = NULL;
		tree[i]->right = NULL;
	}
	root = (node*)malloc(sizeof(node));
	root = tree[1];
	root->left = tree[2];
	root->right = tree[3];
	tree[2]->left = tree[4];
	tree[2]->right = tree[5];
	tree[3]->left = tree[6];
	tree[3]->right = tree[7];
	tree[4]->left = tree[8];
	tree[4]->right = tree[9];
	tree[5]->left = tree[10];
}
//Depth first search for leaves
void Dfs(node* root, int dep)
{
	if (root->left == NULL && root->right == NULL)
	{
		deep[cnt++] = dep;
		return;
	}
	if (root->left != NULL)
		Dfs(root->left, dep + 1);
	if (root->right != NULL)
		Dfs(root->right, dep + 1);
}
//Output deep array
void Print()
{
	for (int i = 0; i < cnt; i++)
		printf("%d%c", deep[i], i == cnt - 1 ? '\n' : ' ');
}
//Determine whether the binary tree is complete
bool Check()
{
	int f = 0;
	for (int i = 1; i < cnt; i++)
	{
		if (deep[i - 1] != deep[i])
		{
			if (deep[i - 1] == deep[i] + 1)
				f++;
			else
				return false;
		}
	}
	if (f <= 1)
		return true;
	return false;
}
int main()
{
	Init();
	Dfs(root, 1);
	Print();
	puts(Check() ? "Yes" : "No");
}

Method 2:

Breadth first search, layer by layer search. When the traversed node is a leaf node, the depth of the leaf node is stored in the array, and finally the number is judged to be the shape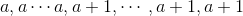Or like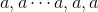If so, then this tree is a complete binary tree, otherwise, it is not a complete binary tree.

Take the tree above as an example and the code is as follows:

#include <bits/stdc++.h>
#define Pair pair<node*,int>
#define ll long long
using namespace std;
struct node
{
	node* left;
	node* right;
}*tree[1005], *root;
int deep[1005], cnt;
//Initialize tree building
void Init()
{
	for (int i = 0; i < 1005; i++)
	{
		tree[i] = (node*)malloc(sizeof(node));
		tree[i]->left = NULL;
		tree[i]->right = NULL;
	}
	root = (node*)malloc(sizeof(node));
	root = tree[1];
	root->left = tree[2];
	root->right = tree[3];
	tree[2]->left = tree[4];
	tree[2]->right = tree[5];
	tree[3]->left = tree[6];
	tree[3]->right = tree[7];
	tree[4]->left = tree[8];
	tree[4]->right = tree[9];
	tree[5]->left = tree[10];
}
//Depth first search for leaves
void Bfs(node* root)
{
	queue<Pair>q;
	q.push(Pair{ root,1 });
	while (!q.empty())
	{
		Pair temp = q.front();
		q.pop();
		if (temp.first->left == NULL && temp.first->right == NULL)
			deep[cnt++] = temp.second;
		if (temp.first->left != NULL)
			q.push(Pair{ temp.first->left ,temp.second + 1 });
		if (temp.first->right != NULL)
			q.push(Pair{ temp.first->right ,temp.second + 1 });
	}
}
//Output deep array
void Print()
{
	for (int i = 0; i < cnt; i++)
		printf("%d%c", deep[i], i == cnt - 1 ? '\n' : ' ');
}
//Determine whether the binary tree is complete
bool Check()
{
	int f = 0;
	for (int i = 1; i < cnt; i++)
	{
		if (deep[i - 1] != deep[i])
		{
			if (deep[i - 1] + 1 == deep[i])
				f++;
			else
				return false;
		}
	}
	if (f <= 1)
		return true;
	return false;
}
int main()
{
	Init();
	Bfs(root);
	Print();
	puts(Check() ? "Yes" : "No");
}