Data structure learning, binary tree

#include<stdio.h>
#include<iostream>

//
using namespace std;

#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define OVERFLOW -1
#define UNSUCCESS 0
#define SUCCESS 1

Other data structures needed (chain stack and chain queue)

//Chain stack
typedef struct LSNode {
	ElemType data;
	struct LSNode* next;
}LSNode,*LStack;

void InitStack_LS(LStack& S);				//Initialize chain stack
void DestroyStack_LS(LStack& S);			//Destroy chain stack
Status StackEmpty_LS(LStack S);				//Judge whether the stack is empty. If it is empty, return TRUE; otherwise, return FALSE
Status Push_LS(LStack& S, ElemType e);		//Push element e onto stack
Status Pop_LS(LStack& S, ElemType& e);		//The top element of stack S is out of the stack and returned with e
Status GetTop_LS(LStack S, ElemType& e);	//Take the top element of stack S and return it with e

typedef struct LQNode {
	ElemType data;
	struct LQNode* next;
}LQNode,*QueuePtr;
typedef struct {
	QueuePtr front;	//Queue head pointer
	QueuePtr rear;	//Tail pointer
}LQueue;

void InitQueue_LQ(LQueue& Q);				//Initialize queue Q
void DestroyQueue_LQ(LQueue& Q);			//Destroy queue Q
Status EnQueue_LQ(LQueue& Q, ElemType e);	//Insert element e at the end of queue Q
Status DeQueue_LQ(LQueue& Q, ElemType& e);	//If the queue Q is not empty, delete the queue header element, use e to return its value, and return OK, otherwise ERROR;

If you want to see the implementation of these two data structures, you can see

Data structure learning, chain queue

Data structure learning, chain stack

The structure of the binary tree used (binary linked list)

typedef struct BITNode {
	TElemType data;            //Data domain
	struct BITNode* lchild;    //Left child
	struct BITNode* rchild;    //Right child
}BiTNode, * BiTree, * ElemType;

Its basic operation interface

void InitBiTree(BiTree& T);							//Create an empty binary tree
BiTree MakeBiTree(TElemType e, BiTree L, BiTree R);	//Create a binary tree, where the value of the root node is e, and L and R are the left subtree and right subtree respectively
void DestroyBitree(BiTree& T);						//Destroy binary tree
Status BiTreeEmpty(BiTree T);						//Empty binary tree
Status BreakBiTree(BiTree& T, BiTree& L, BiTree& R);//Decompose a binary tree T into three parts: root, left subtree and right subtree	
Status ReplaceLeft(BiTree& T, BiTree& LT);			//Replace the left subtree. If t is not empty, replace the left subtree of T with LT and return the original left subtree of T with Lt
Status ReplaceRight(BiTree& T, BiTree& RT);			//Replace the right subtree. If t is not empty, replace the right subtree of T with RT, and return the original right subtree of T with RT
//Advanced operation
Status visit(TElemType a);
//Recursive traversal
Status PreOrderTraverse(BiTree T, Status(*visit)(TElemType));	//Preorder
Status InOrderTraverse(BiTree T, Status(*visit)(TElemType));	//Middle order
Status PostOrderTraverse(BiTree T, Status(*visit)(TElemType));	//Post order
int BiTreeDepth(BiTree T);										//Returns the depth of the binary tree
void CountLeaf(BiTree T, int& count);							//Count the leaves of binary tree T with count
BiTree CreateBiTree(char* defBT, int& i);						//Construction of binary tree by preorder
//Non recursive traversal
void LevelOrderTraverse(BiTree T, Status(*visit)(TElemType));	//level traversal 
Status PreOrderTraverse_U(BiTree T, Status(*visit)(TElemType));	//Preorder non recursive
Status InOrderTraverse_U(BiTree T, Status(*visit)(TElemType));	//Medium order non recursive
Status PostOrderTraverse_U(BiTree T, Status(*visit)(TElemType));//Postorder non recursive

basic operation

Create an empty binary tree

void InitBiTree(BiTree& T)
{
	T = NULL;
}

Create a binary tree, where the value of the root node is e, and L and R are the left subtree and right subtree respectively

BiTree MakeBiTree(TElemType e, BiTree L, BiTree R)
{
	BiTree T;
	T = (BiTree)malloc(sizeof(BiTNode));
	if (T != NULL)
	{
		T->data = e;
		T->lchild = L;
		T->rchild = R;
		return T;
	}
	else
	{
		return NULL;
	}
}

Destroy binary tree

void DestroyBitree(BiTree& T)
{
	if (T != NULL)//Simple and crude recursion
	{
		DestroyBitree(T->lchild);
		DestroyBitree(T->rchild);
		free(T);
	}
}

Empty binary tree

Status BiTreeEmpty(BiTree T)
{
	if (T == NULL)
	{
		return TRUE;
	}
	else
	{
		return ERROR;
	}
}

Decompose a binary tree T into three parts: root, left subtree and right subtree

Status BreakBiTree(BiTree& T, BiTree& L, BiTree& R)
{
	if (T != NULL)
	{
		L = T->lchild;
		R = T->rchild;
		T->lchild = NULL;
		T->rchild = NULL;
		return OK;
	}
	else
	{
		return OVERFLOW;
	}
}

Replace the left subtree. If t is not empty, replace the left subtree of T with LT and return the original left subtree of T with Lt

Status ReplaceLeft(BiTree& T, BiTree& LT)
{
	BiTree temp;
	if (T != NULL)
	{
		temp = T->lchild;
		T->lchild = LT;
		LT = temp;
		return OK;
	}
	else
	{
		return ERROR;
	}
}

Replace the right subtree. If t is not empty, replace the right subtree of T with RT, and return the original right subtree of T with RT

Status ReplaceRight(BiTree& T, BiTree& RT)
{
	BiTree temp;
	if (T != NULL)
	{
		temp = T->rchild;
		T->rchild = RT;
		RT = temp;
		return OK;
	}
	else
	{
		return ERROR;
	}
}

Advanced operation

//Access function

Status visit(TElemType a)
{
	if (a != '#')
	{
		printf("%c", a);
		return OK;
	}
	else
	{
		return ERROR;
	}
}

Recursive traversal

Preorder traversal binary tree

Status PreOrderTraverse(BiTree T, Status(*visit)(TElemType))
{
	if (T == NULL)
	{
		return OK;
	}
	if (visit(T->data) == ERROR)//root
	{
		return ERROR;
	}
	if (PreOrderTraverse(T->lchild, visit) == ERROR)//Left
	{
		return ERROR;
	}
	if (PreOrderTraverse(T->rchild, visit) == ERROR)//right
	{
		return ERROR;
	}
	return OK;
}

Middle order traversal binary tree

Status InOrderTraverse(BiTree T, Status(*visit)(TElemType))
{
	if (T == NULL)
	{
		return OK;
	}
	if (InOrderTraverse(T->lchild, visit) == ERROR)//Left
	{
		return ERROR;
	}
	if (visit(T->data) == ERROR)//root
	{
		return ERROR;
	}
	if (InOrderTraverse(T->rchild, visit) == ERROR)//right
	{
		return ERROR;
	}
	return OK;
}

Postorder traversal binary tree

Status PostOrderTraverse(BiTree T, Status(*visit)(TElemType))
{
	if (T == NULL)
	{
		return OK;
	}
	if (PostOrderTraverse(T->lchild, visit) == ERROR)//Left
	{
		return ERROR;
	}
	if (PostOrderTraverse(T->rchild, visit) == ERROR)//right
	{
		return ERROR;
	}
	if (visit(T->data) == ERROR)//root
	{
		return ERROR;
	}
	return OK;
}

Returns the depth of the binary tree

int BiTreeDepth(BiTree T)
{
	int depthLeft, depthRight;
	if (T == NULL)
	{
		return 0;
	}
	else
	{
		depthLeft = BiTreeDepth(T->lchild);
		depthRight = BiTreeDepth(T->rchild);
		return 1 + (depthLeft > depthRight ? depthLeft : depthRight);
	}
}

Count the leaves of binary tree T with count

void CountLeaf(BiTree T, int& count)
{
	if (T != NULL)
	{
		if (T->lchild == NULL && T->rchild == NULL)
		{
			count++;
		}
		CountLeaf(T->lchild, count);
		CountLeaf(T->rchild, count);
	}
}

Construction of binary tree by preorder

BiTree CreateBiTree(char* defBT, int& i)
{
	BiTree T;
	TElemType ch;
	ch = defBT[i++];
	if (ch == '#')
	{
		InitBiTree(T);
	}
	else
	{
		T = MakeBiTree(ch, NULL, NULL);
		T->lchild = CreateBiTree(defBT, i);
		T->rchild = CreateBiTree(defBT, i);
	}
	return T;
}

Non recursive traversal

level traversal

void LevelOrderTraverse(BiTree T, Status(*visit)(TElemType))
{
	if (T != NULL)
	{
		LQueue Q;
		InitQueue_LQ(Q);
		BiTree p = T;
		visit(p->data);
		EnQueue_LQ(Q, p);
		while (DeQueue_LQ(Q, p) == OK)
		{
			if (p->lchild != NULL)
			{
				visit(p->lchild->data);
				EnQueue_LQ(Q, p->lchild);

			}
			if (p->rchild != NULL)
			{
				visit(p->rchild->data);
				EnQueue_LQ(Q, p->rchild);
			}
		}
		DestroyQueue_LQ(Q);
	}
}

The following three non recursive traversals can be seen

I can only say that this is a big manhttps://blog.csdn.net/Benja_K/article/details/88389039

Preordered non recursive traversal

Status PreOrderTraverse_U(BiTree T, Status(*visit)(TElemType))
{
	BiTree p;
	p = T;
	LStack S;
	InitStack_LS(S);
	while (p != NULL || StackEmpty_LS(S) != TRUE)
	{
		if (p != NULL)
		{
			Push_LS(S, p);
			visit(p->data);
			p = p->lchild;
		}
		else
		{
			Pop_LS(S, p);
			p = p->rchild;
		}
	}
	DestroyStack_LS(S);
	return OK;
}

Medium order non recursive traversal

Status InOrderTraverse_U(BiTree T, Status(*visit)(TElemType))
{
	BiTree p;
	p = T;
	LStack S;
	InitStack_LS(S);
	while (p != NULL || StackEmpty_LS(S) != TRUE)
	{
		if (p != NULL)
		{
			Push_LS(S, p);		
			p = p->lchild;
		}
		else
		{
			Pop_LS(S, p);
			visit(p->data);
			p = p->rchild;
		}
	}
	DestroyStack_LS(S);
	return OK;
}

Postorder non recursive traversal

Status PostOrderTraverse_U(BiTree T, Status(*visit)(TElemType))
{
	LStack S;
	InitStack_LS(S);
	int top = -1;
	int Stack[15];   
	BiTNode* p = T;
	while (p != NULL || StackEmpty_LS(S) != TRUE)
	{
		if (p != NULL) {     
			Push_LS(S, p);
			top++;
			Stack[top] = 1;
			p = p->lchild;
		}
		else 
		{
			if (Stack[top] == 1) 
			{  
				GetTop_LS(S, p);
				Stack[top] = 2;
				p = p->rchild;
			}
			else 
			{         
				Pop_LS(S, p);
				top--;
				visit( p->data);    
				p = NULL;      
			}
		}
	}
	DestroyStack_LS(S);
	return OK;
}

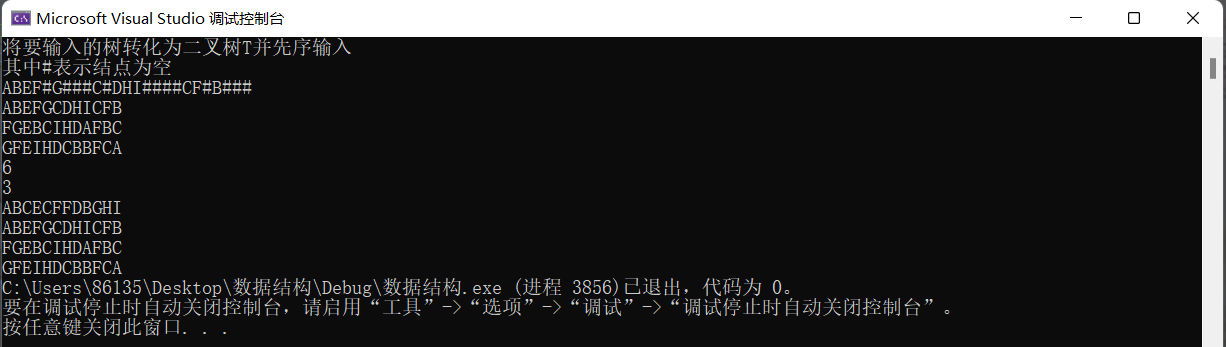
Testing of some interfaces

The binary tree tested is

int main()
{
	//ABEF#G###C#DHI####CF#B#### / / preamble
	char defBT[100] = { '#' };
	if (defBT != NULL)
	{
		printf("Convert the tree to be imported into a binary tree T And input in sequence\n");
		printf("among#Indicates that the node is empty. \ n "");
		//scanf("%s", defBT);
		cin >> defBT;
		getchar();
	}
	else
	{
		return ERROR;
	}
	BiTree T;
	int i = 0;
	T = CreateBiTree(defBT, i);
	PreOrderTraverse(T, visit);
	cout << "\n";
	InOrderTraverse(T, visit);
	cout << "\n";
	PostOrderTraverse(T, visit);
	cout << "\n";
	
	cout << BiTreeDepth(T) << endl;
	int j = 0;
	CountLeaf(T, j);
	cout << j << endl;
	LevelOrderTraverse(T, visit);
	cout << "\n";
	PreOrderTraverse_U(T, visit);
	cout << "\n";
	InOrderTraverse_U(T, visit);
	cout << "\n";
	PostOrderTraverse_U(T, visit);
}

There are many operations for binary tree, such as the copy of binary tree, the search of binary tree, how many nodes the binary tree has, and whether the binary tree is a complete binary tree, which is left to you to realize by yourself.

Keywords: C C++ data structure

Added by fred_belanger on Sun, 06 Feb 2022 22:12:55 +0200

Programming VIP