Question 1: sequence table insertion

[problem description]
Let the data elements in sequence table A increase in order, try to write A program to insert x into the appropriate position of the sequence table so that the table is still orderly.
[input]
Initial sequence table, insert position, insert element.
[output]
Sequence table after inserting elements.
[storage structure]
Adopt sequential storage structure
[basic idea of algorithm]
Create sequence table: create a sequence table using the default initial allocation quantity, and create a corresponding sequence table according to the entered initial sequence table; Insert element: find the insertion position in the sequence table according to the read elements, move the elements at the original position and the subsequent elements backward one by one from the last, and then insert the element; Print sequence table: print each element in sequence starting from the first element of the sequence table.

#include <stdio.h>
#define maxSize 100
typedef struct{
	int date[maxSize]; //Similar to the creation of an array, space is allocated statically 
	int length;
}sqList;

void initSqList(sqList &L, int length){
	//Creation of sequence table 
	int i;
	int x;
	L.length = length;
	printf("Please enter the order table A have\n");
	for(i = 0; i < length; i++){
		scanf("%d", &x);
		L.date[i] = x;
	}
}

int insertElem(sqList &L, int x, int n){
	//In linear table L, insert x at position n
	int i;
	if(n < 0 || n > L.length || L.length == maxSize)
		//Conditional judgment of linear table 
		return 0;
	for(i = L.length - 1; i >= n - 1; i--){
		//Movement of elements after insertion position 
		L.date[i + 1] = L.date[i]; 
	}
	L.date[n - 1] = x;
	L.length ++;
	return 1;
}

int main(){
	sqList sq;
	int i;
	printf("Please enter the sequence table A Length of\n"); 
	int length;
	scanf("%d", &length);
	initSqList(sq, length);
	printf("Please enter the insert element:");
	int x;
	scanf("%d", &x);
	printf("Please enter the insertion location:");
	int n;
	scanf("%d", &n);
	int insert;
	insert = insertElem(sq, x, n);
	if(insert == 0)
		printf("Insert failed:");
	if(insert == 1)
		printf("Insert successful:");
	for(i = 0; i < sq.length; i++){
		printf("%d ",sq.date[i]);
	}
}

Result demonstration:

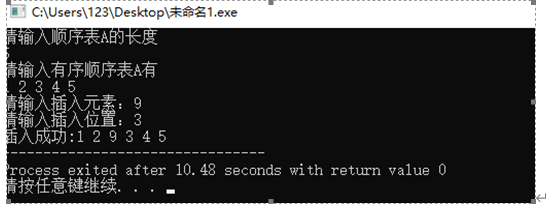
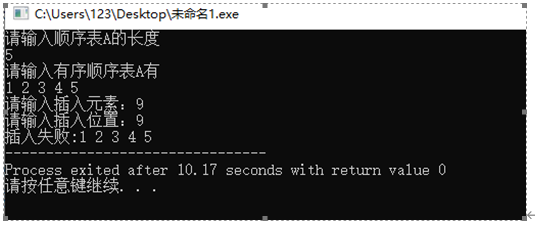
Results and analysis:
(1) Advantages: the insertion function is realized, and the condition judgment is carried out. (2) Disadvantages: the robustness of the code is poor, and some extreme cases are not considered. (3) Time complexity: O(n) (4) space complexity: O(n)

Question 2: polynomial chain storage

[problem description]
The polynomial a (x) = a0+a1x1+a2x2 +... + anxn (where aI is a non-zero coefficient) is stored in the single linked list ha, and the polynomial B (x) = b0+b1x1+b2x2 +... + bmxm (where bj is a non-zero coefficient) is stored in the single linked list hb. It is required to calculate C (x) = a (x) + B (x), and the results are stored in the single linked list hc. Try to write the program.
[input]
Initialize the single linked list and create A and B linked lists.
[output]
A. B linked list and C linked list.
[storage structure]
Chain storage structure is adopted
[basic idea of algorithm]
Establish A single linked list: construct A single linked list node, including three fields, and record the coefficient, index and next element respectively; Store linked lists A, B and list summation: traverse the linked lists A and B at the same time. If the exponents are the same, add them to C respectively. Store them in C and output the linked list C

#include <stdio.h>
#include <malloc.h>
#define NULL 0
typedef struct LNode{
	int a; //coefficient 
	int b; //index 
	struct LNode *next;
}LNode, *node;

void initLNode(node &L){
	//The binomial is stored in the list, and the & reference pointer is used to modify the argument 
	int i;
	int length;
	node p, q;
	L = (node)malloc(sizeof(LNode)); //Node space application of header 
	p = L;
	printf("Please enter the number of items of polynomial:");
	scanf("%d",&length);
	for(i = 1; i <= length; i++){
		//Node creation 
		q = (node)malloc(sizeof(LNode));
		printf("Please enter page%d Coefficient of term",i);
		scanf("%d",&q->a);
		printf("Please enter page%d Index of term",i);
		scanf("%d",&q->b);
		p->next = q;
		p = q;
	}
	p->next = NULL;
}

node addLNode(node A, node B){
	//Binomial addition implementation 
	node C;
	C = (node)malloc(sizeof(LNode));
	node p, q, r, s; //Auxiliary pointer 
	p = A->next; 
	q = B->next;
	r = C;
	while(p != NULL && q != NULL){
		//Traverse a and B linked lists at the same time 
		s = (node)malloc(sizeof(LNode));
		if(p->b == q->b){
			//Same index
			s->a = p->a + q->a;
			s->b = p->b;
			r->next = s;
			p = p->next;
			q = q->next;
			r = s;
		}
		//When the pointer is different, the one with small index shall be inserted first 
		else if(p->b < q->b){
			s->a = p->a;
			s->b = p->b;
			r->next= s;
			p = p->next;
			r = s;
		}
		else{
			s->a = q->a;
			s->b = q->b;
			r->next = s;
			q = q->next;
			r = s;
		}
		//When one linked list is empty, the other directly inserts the rest 
		if (p != NULL){
			r->next = p;
		}
		if (q != NULL){
			r->next = q;
		}
	}
r->next = NULL; //Ensure that the trailing node is followed by a null pointer
	return C;
}

void showLNode(node L){
	//Traversal display linked list 
	node p;
	p = L->next;
	while(p!= NULL){
		printf("Coefficient is%d",p->a);
		printf("Index is%d  ",p->b);
		p = p->next;
	}
	printf("\n");
}

int main(){
	node A;
	initLNode(A);
	node B;
	initLNode(B);
	node C = addLNode(A, B);
	printf("A:");
	showLNode(A);
	printf("B:");
	showLNode(B);
	printf("C:");
	showLNode(C);
}

Result demonstration:

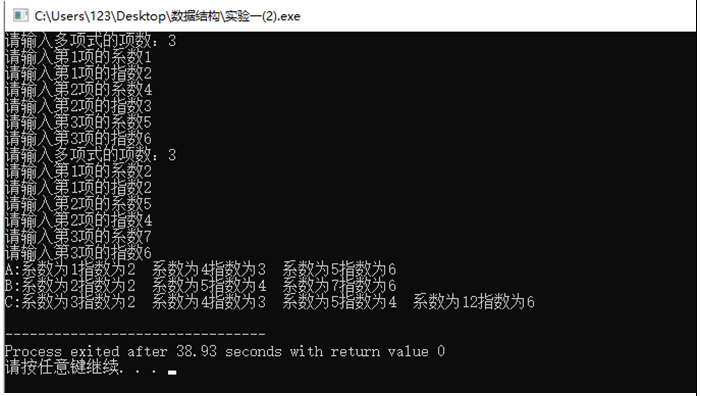
Results and analysis:
(1) Advantages: it realizes the storage and addition of polynomials using linked list. (2) Disadvantages: the expression form of the code is poor, and the index must be input from small to large. (3) Time complexity: O(n) (4) space complexity: O(n), depending on the number of terms of the polynomial.

Question 3: Josephus problem

[problem description]
There are n people sitting around a round table. Now start counting from the s person, count to the m person, then start counting again from the next person, and count to the m person again. Repeat until all people are listed. The Josephus problem is: for any given n, m, s, find the sequence table of n people obtained according to the column order.
[input]
Enter n individuals, the number m, starting with s.
[output]
The sequence table of n personnel obtained according to the listing order.
[storage structure]
Chain storage structure is adopted
[basic idea of algorithm]
Build a single cycle linked list: according to the number of people n, establish n nodes without head nodes, and assign the data field of each node as 1, 2, 3, and so on. Output sequence table: the first time is the node of s + m, and then M cycles can be performed until the linked list is empty.

#include <stdio.h>
#include <malloc.h>
typedef struct LNode{
	int a;
	struct LNode *next;
}LNode, *node;

void initLNode(node &L, int n){
	//Create circular linked list 
	L = (node)malloc(sizeof(LNode)); //Head node space application 
	int i;
	node p, q;
	p = L;
	p->a = 1;
	for(i = 1; i < n; i ++){
		//Node insertion 
		q = (node)malloc(sizeof(LNode));
		q->a = i + 1;
		p->next = q;
		p = q;
	}
	p->next = L;
}

void showOut(node L, int n, int m, int s){
	//Output game results 
	int i;
	node p, q;
	p = L;
	for(i = 0; i < m + s - 3; i++){
		//Location of the first queue 
		p = p->next;
	}
	q = p->next;
	printf("%d ", q->a);
	p->next = q->next;
	free(q);
	int count = 1;
	while(1){
		//Loop traversal 
		for(i = 0; i < m - 1; i++){
			//Operation satisfying out of column position 
			p = p->next;
		}
		q = p->next;
		printf("%d ", q->a);
		p->next = q->next;
		free(q);
		count++;
		if(count == n){
			//Counter, end condition 
			break;
		} 
	}
}
 
int main(){
	int n;
	int m;
	int s;
	printf("Please enter the number of people:");
	scanf("%d", &n); 
	printf("Please enter the specified number:");
	scanf("%d", &m);
	printf("Please enter start location:");
	scanf("%d", &s);
	node L;
	initLNode(L, n);
	showOut(L, n, m, s);
}

Result demonstration:

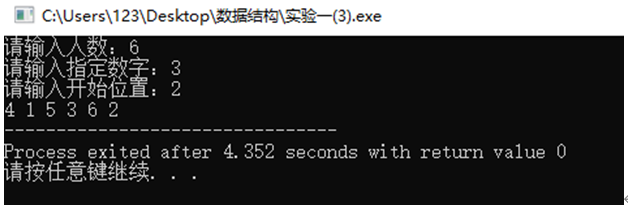
Results and analysis:
(1) The advantage is that the problem is solved by using the circular linked list without head nodes. (2) Disadvantages: the code is cumbersome. (3) Time complexity: O (mn) analysis: the linked list should be traversed from 1 to m every time, and each number needs to be output, that is, n times. (4) Spatial complexity O (n)

Experience

1. Re learn C language and improve the understanding of the structure of C language.
2. Realize the data structure through the structure.
3. For the sequential list, you can create a simple structure through the array, while for the linked list, you must make < malloc h> The malloc function under the header file creates a node and creates a linked list through the pointer of the node.
4. When forming two linked lists into a linked list: you must judge whether the two linked lists are empty at the same time. For example (P! = null & & Q! = null). When one is empty, it can be directly connected to the node that is not empty.
5. The establishment and use of the circular linked list: connect the last node with the first source node, and judge whether the circular linked list is empty by counting.