How search works

Find concepts

• Let the record table L = (R1,R2,R3... Rn), where R (1 < = I < = n) is the record. For a given value k, the process of determining the record with key=k in Table L is called search.
• If there is a record Ri with key=k in the table, it is recorded as Ri key=k, the search succeeds, and the sequence number i (or Ri address) of the record in Table L is returned; otherwise (search fails), 0 (or null address) is returned.

Search of sequence table
Half search: for a given value k, gradually determine the interval of the record to be checked, and reduce the search space by half (half) each time until the search succeeds or fails.
Set two cursors low and high to point to the upper bound (header) and lower bound (footer) of the current table to be searched, and mid to the middle element.
Hash table lookup: for a given K, the required records can be obtained without any comparison. The time complexity of the lookup is constant level O ©. When searching for a record with key=k, the address of the corresponding record can be obtained through the relationship F, thus eliminating the key comparison process. This relationship f is the so-called hash function (or hash function), which is recorded as H(key). In fact, it is an address mapping function. Its argument is key and the function value is the storage address of the record (or your hash address). Different keys may get the same hash address, that is, when key1!=key2, there may be H(key1)=H(key2). At this time, key1 and key2 are synonymous words. This phenomenon is called "conflict" or "collision", Because a data unit can only store one record. Generally, the selection of hash function can only reduce the conflict as much as possible, but it is impossible to completely avoid it. This requires that after the conflict occurs again, find an appropriate method to solve the problem of storing conflict records.

There are many methods to select (or construct) hash functions. The principle is to evenly distribute records as much as possible to reduce conflicts. There are several common methods:
Direct address method, square middle method, superposition method, retained remainder method.

	Retained remainder method: also known as prime number division method, set Hash Tablespace length is m,Select one not greater than m Prime number of p,Order: H(key)=key%p
						If take p=19(Prime number), also given on key aggregate k，have key:28,35,63,77,105       H(key)=key%19:9,16,6,1,10    H(key)Random reading is much better.

	Method to deal with conflict: select the one with good randomness hash Function can reduce the occurrence of conflicts. Generally speaking, conflicts cannot be completely avoided. Set hash The table address space is 0~m-1(Table length m).
								At address j Find a free cell in front of or behind the to store conflicting records, or pull the conflicting records into a linked list.
								Another factor is the filling factor of the table&(Alpha),&=n/m,among m Is the table length, n Is the number of records in the table, generally&At 0.7-0.8 In order to reduce conflict accumulation, the table maintains a certain idle margin.

							Open address method: when a conflict occurs, the H(key)Find a free cell to store conflicting records before and after H(key)Get the next address based on: Hi=(H(key)+di)%m;   m Is the table length,%Operation is the guarantee Hi Fall at [0, m-1]section,di Is the address increment, di There are many ways to choose.
							(1)di=1,2,3,....(m-1)---------------------------Called linear probing
							(2)1 Square of,-1 Square of, square of 2,-2 Square of-----------It is called secondary exploration method
							Set record key aggregate k={23,34,14,38,46,16,68,15,07,31,26}Number of records n=11
							H(key)=key%13
							Hi(H(key)+di)%15;  di=1,2,3,4....(m-1)
	
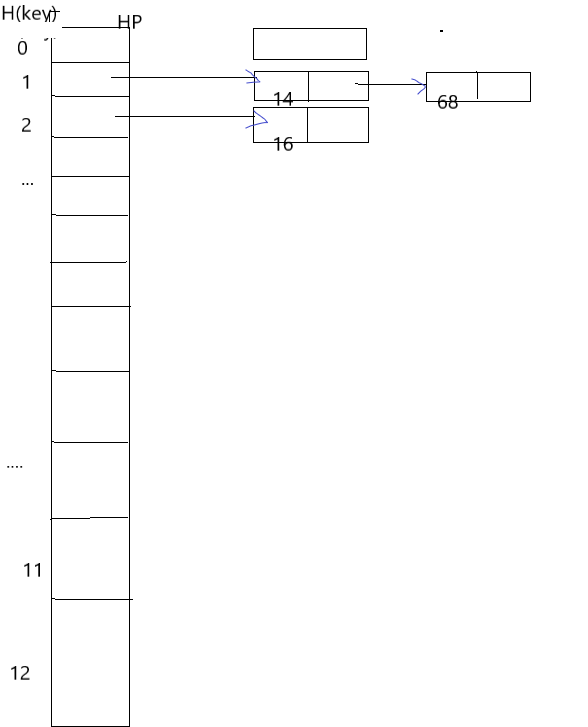
							Chained address method: Set H(key)The value range (value range) is [0, m-1]，Create header pointer vector HP[m],HP[i](0<=i<=m-1)The initial value is empty.
													set up H(key)=key%13,k={23,34,14,38,46,16,68,15,07,31,26}.，Chain storage conflict. Key value pair( key),Value( H(key))
							The advantages of chain address method in conflict resolution: no aggregation and easy to delete the data in the table.

hash.h
#ifdef_HASH_H
#define _HASH_H

#define N  15
typedef int datatype ;
typedef struct node{
	datatype key;
	datatype value;
	strcut node *next;
}listnode ,*linklist;

typedef strcut {
	listnode data[N];
}hash;

hash *hash_create();
int hash_insert(hash *HT,datatype key);
linklist *hash_search(hash *HT,datatype key);

#endif
 

hash.c
#include<stdio.h>
#include"hash.h"
#include<string.h>
#include<stdlib.h>
hash *hash_create()
{
	if((HT=(hash *)malloc(sizeof(hash)))==NULL){
		printf("malloc failed\n");
		return NULL;
	}
	memset(HT,0,sizeof(hash));
	return HT;

}
int hash_insert(hash *HT,datatype key)
{
	linklist p;
	if(HT==NULL){
		printf("HT is null\n");
		return -1;
	}
	if((p=(linklist )malloc(sizeof(listnode)))==NULL){
		printf("malloc is failed\n");
		return -1;
	}
	p->key=key;
	p->vlue=key%N;
	p->next=NULL;
	
	q=&(HT->data[key%N]);
	while(q->next&&q->next->key<p->key){
		q=q->next;
	}
	p->next=q->next;
	q->next=p;
	return 0;

}
linklist *hash_search(hash *HT,datatype key)
{
	linklist p;
	if(HT==NULL){
		printf("HT is null\n");
		return -1;
	}
	p=&(HT->data[key%N]);  //Head node
	while(p->next&&p->next->ke!=key){
		p=p->next;
	}
	if(p->next==NULL){
		return NULL;
	}else{
		printf("found\n");
		return p->next;
	}
}

test.c
#include<stdio.h>
#include"hash.h"
int main(int argc,char *argv[])
{
	hash *HT;
	int data[]={23,34,14,38,46,16,68,15,07,31,26};
	int i;
	linklist r;
	if(HT==NULL){
		return -1;
	}
	for(i=0;i<sizeof(data)/sizeof(int);i++){
		hash_insert(HT,data[i]);
	}

	printf("input:);
	scanf("%d",&key);
	r=hash_search(HT,key);
	if(r==NULL)
		printf("r not found\n");
	else
		printf("found:%d %d\n",key,r->key);
	
	return 0;
}