1, Type definition of queue

A queue is a linear table that is limited to inserting only at the end of the table and deleting only at the header. The tail of the table is called the rear, the header is called the front, and the table without elements is called an empty queue.

In addition to all the characteristics of linear table, queue has its own unique properties. It has a first in first out (FIFO) structure.

Queue up: the operation of inserting elements; Out of queue: delete element.

Set the queue size to MAXQSIZE. If rear = MAXQSIZE, overflow occurs, and there are two overflow situations:

True overflow: in the case of overflow, the team head points to the base address (indicating that there is no free space in the team); False overflow: in the case of overflow, the queue head does not point to the base address (indicating that the free space in the queue is not used).

There are two representations of queues (storage methods): one is sequential structure storage, which is called sequential queue; The other is chain structure storage, which is called chain queue. This will be described later.

Basic operations of queue:

InitQueue(&Q)    // Construct an empty queue Q
DestroyQueue(&Q)    // Destroy queue Q
ClearQueue(&Q)    // Clear Q to empty queue
IsEmpty(Q)    // Judge whether queue Q is an empty queue
QueueLength(Q)    // Returns the length of queue Q
GetHead(Q, &e)    // Return the queue header element of Q with e
EnQueue(&Q, e)    // Insert element e as a new tail element
DeQueue(&Q, &e)    // Delete the queue header element of Q and return it with e

2, Sequential queue (cyclic queue)

Sequential queue uses a group of storage units with continuous addresses to store the elements from the head of the queue to the end of the queue. In addition, two pointers front and rear need to be attached to indicate the positions of the head and end of the queue elements respectively.

Graphical structure of sequential queue:

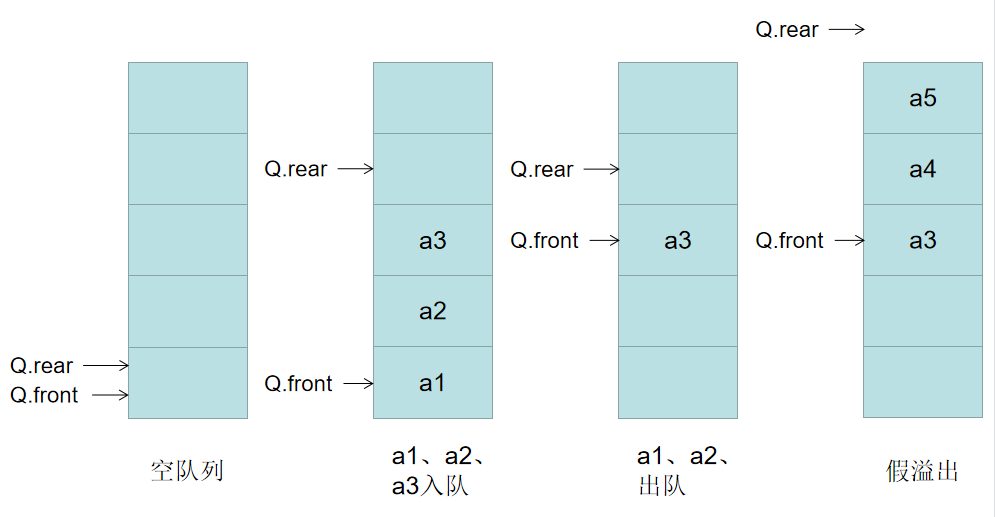
Because the queue has the characteristics of first in first out, the above problems will occur during sequential storage, that is, the space after the elements are out of the queue is wasted, so that the sequential queue space is not full, but it is impossible to continue to let new elements join the queue, and it is too wasteful to continue to allocate new space to it.

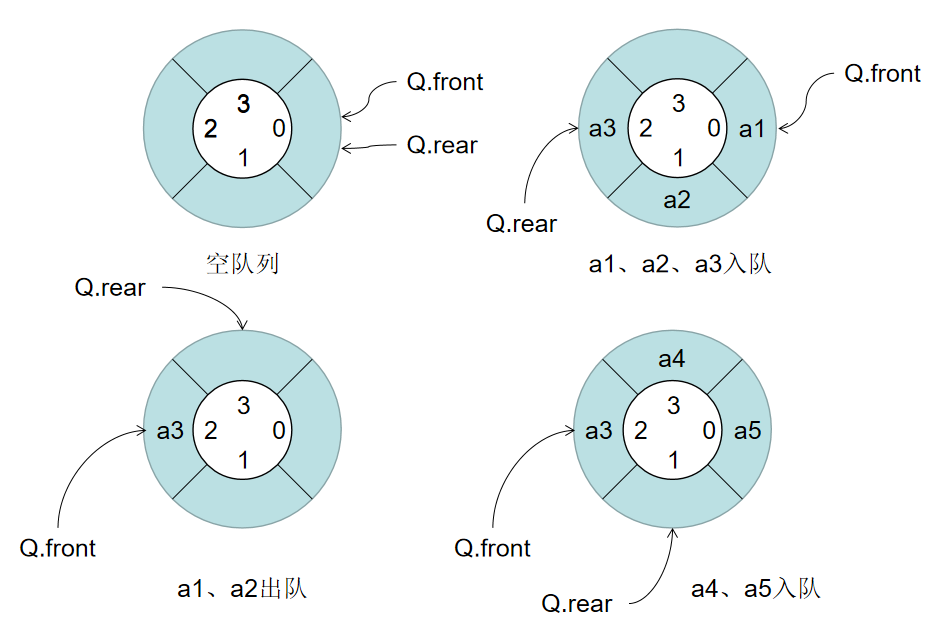
An ingenious way to solve this problem is to imagine the sequential queue as a circular space, which is called circular queue, so that the space of the elements that have been out of the queue can be used again.

There are two methods for circular queue to judge whether the queue is empty or full. One is to set another flag bit to judge whether the queue is empty or full;

The other is to discard the space of an element and judge whether the queue is full by judging whether the queue head pointer is at the next position of the tail pointer.

Generally speaking, the second storage method is adopted, and a space is abandoned to standardize the judgment of the queue.

Graphic structure of circular queue:

Code implementation of circular queue:

1. Storage structure:

#define MAXQSIZE 100 / / maximum queue length
typedef struct{
    QElemType *base;    // Initialized dynamically allocated storage space
    int front;    // Header pointer. If the queue is not empty, it points to the queue header element
    int rear;    // Tail pointer, if the queue is not empty, points to the next position of the tail element of the queue
}SqQueue;

2. Initialization:

Status InitQueue(SqQueue &Q){
    // Construct an empty queue Q
    Q.base = (QElemType *)malloc(MAXQSIZE * sizeof(QElemType));
    if(!Q.base) exit(OVERFLOW);    // Storage allocation failed
    Q.front = Q.rear = 0;    // The initialization head pointer and tail pointer are both at 0
    return OK;
} // InitQueue

Time complexity: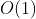

3. Length calculation:

int QueueLength(SqQueue Q){
    // Returns the number of elements in queue Q, that is, the length of the queue
    return ((Q.rear - Q.front + MAXQSIZE) % MAXQSIZE);
} // QueueLength

Time complexity: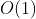 

4. Join the team:

Status EnQueue(SqQueue &Q, QElemType e){
    // Insert a new tail element with element e as Q
    if((Q.rear + 1) % MAXQSIZE == Q.front) return ERROR;    // The queue is full
    Q.base[Q.rear] = e;    // Insert element e
    Q.rear = (Q.rear + 1) % MAXQSIZE;    // rear points to the next empty location
    return OK;
} // EnQueue

Time complexity: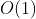 

5. Out of team operation:

Status DeQueue(SqQueue &Q, QElemmType &e){
    // Delete the queue header element of Q and return its value with e
    if(Q.front == Q.rear) return ERROR;    // Queue is empty
    e = Q.base[Q.front];    // Assign the team head element to e
    Q.front = (Q.front + 1) % MAXQSIZE;    // front points to the next element
    return OK;
} // DeQueue

Time complexity: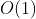 

6. Take the team head:

SElemType GetHead(SqQueue Q){
    // Returns the queue header element without deleting it
    if(Q.front != Q.rear)    // Queue is not empty
        return Q.base[Q.front];    // Returns the queue header pointer element
} // GetHead

Time complexity: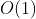 

3, Chain queue

A chain queue is a queue represented by a linked list. A chain queue can only be determined when the head pointer and tail pointer point to the head and tail of the queue respectively. For the convenience of operation, add a head node to the chain queue and make the head pointer point to the head node. In this way, the judgment condition of empty queue is that the head and tail pointers point to the head node.

Graphic structure of chain queue:

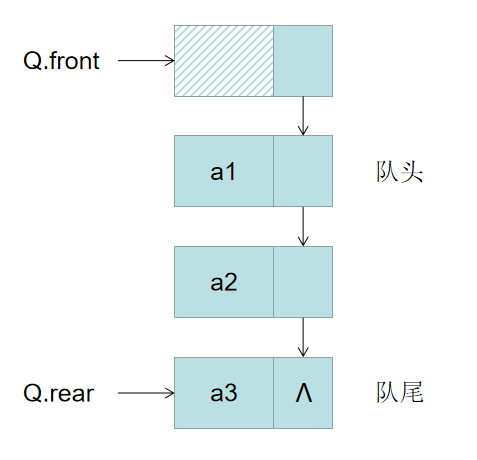
Code implementation of chain queue:

1. Storage structure:

typedef struct QNode{
    QElemType data;    // data elements
    struct QNode *next;    // Pointer element
}QNode, *QueuePtr;

typedef struct{
    QueuePtr front;    // Queue head pointer
    QueuePtr rear;    // Tail pointer
}LinkQueue;

2. Initialization:

Status InitQueue(LinkQueue &Q){
    // Construct an empty queue Q
    Q.front = Q.rear = (QueuePtr)malloc(sizeof(QNode));
    if(!Q.front) exit(OVERFLOW);    // allocation failed
    Q.front->next = NULL;    // The queue head pointer is initialized to null
    reutrn OK;
} // InitQueue

Time complexity: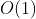

3. Destruction:

Status DestroyQueue(LinkQueue &Q){
    // Destroy queue Q
    while(Q.front){    // Start from the first node and delete each node circularly
        Q.rear = Q.front->next;
        free(Q.front);
        Q.front = Q.rear;
    }
    return OK;
} // DestroyQueue

Time complexity: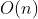 

4. Join the team:

Status EnQueue(LinkQueue &Q, QElemType e){
    // Insert a new tail element with element e as Q
    p = (QueuePtr)malloc(sizeof(QNode));    // Create a new node p
    if(!p) exit(OVERFLOW);    // allocation failed
    p->data = e;    // Assign e to the value of p node
    p->next = NULL;    // p node pointer is null
    Q.rear->next = p;    // The pointer of the queue end node points to the p node
    Q.rear = p;    // The tail pointer points to p
    return OK;
} // EnQueue

Time complexity: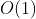 

5. Out of team operation:

Status DeQueue(LinkQueue &Q, QElemType &e){
    // Delete the queue header element of Q and return its value with e
    if(Q.front == Q.rear) return ERROR;    // If the queue is empty
    p = Q.front->next;    // p points to the team head node
    e = p->data;    // Assign a value to e
    Q.front->next = p->next;    // The header pointer points to the new queue header node
    if(Q.rear == p) Q.rear = Q.front;    // p points to the end of the queue, then only the end of the queue element remains in the queue, and the queue is empty after release
    free(p);    // Release node
    return OK;
} // DeQueue

Time complexity: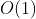 

6. Take the team head:

QElemType GetHead(LinkQueue Q, QElemType &e){
    // Use e to return the queue header element of chain queue Q without leaving it out of the queue
    if(Q.front == Q.rear) return ERROR;    // If the queue is empty
    e = Q.front->next->data;
    return OK;
} // GetHead

Time complexity: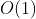 

summary

Based on the characteristics of queue first in first out, it is often used to solve the queuing problem. The first in the queue is the first out of the queue, and the last in the queue is the last out of the queue, so as to achieve an orderly effect.

In addition, most of the basic operation time complexity of the queue is very small, but the disadvantage is that elements can only be taken out at the head of the queue and inserted at the end of the queue.