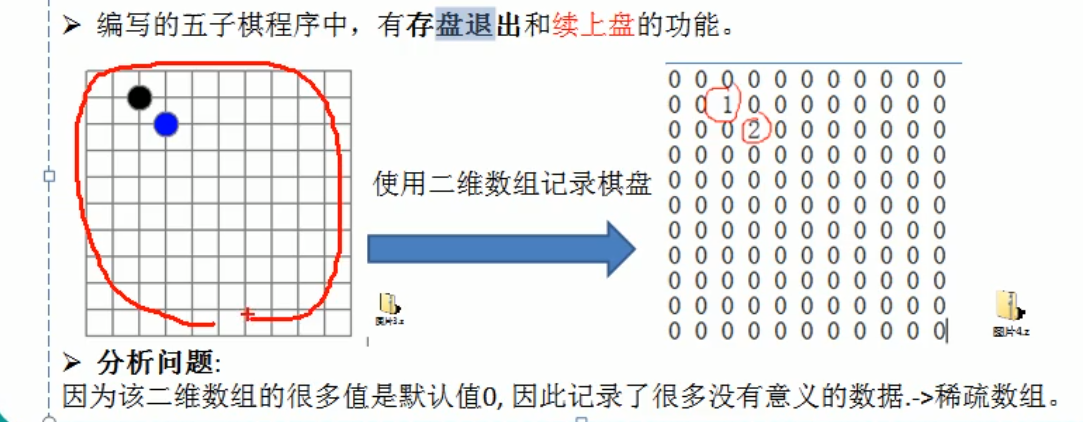
data structure
Sparse array

queue
Queue introduction
-
Queue is a sequential list, which can be realized by array or linked list
-
Follow FIFO rules. That is, the data stored in the queue should be taken out first. After storage, take it out
-
Sketch Map:
Array simulation queue
-
The queue itself has a sequence table. If the structure of the array is used to store the data of the queue, the declaration of the queue array is shown in the figure below, where maxSize is the maximum capacity of the queue
-
The output and input of the queue are processed from the front and back ends respectively. Therefore, use two variables front and rear to record the subscripts at the front and back ends of the queue respectively. The front will change with the data output, while the rear will change with the data input
-
When we store data into the queue, it is called "addQueue". The processing of addQueue needs two steps:
-
Move the tail pointer back: rear+1. When front == rear, there is no data in the queue
-
If the tail pointer rear is less than the maximum subscript maxSize-1 of the queue, the data will be stored in the array element referred to by rear, otherwise the data cannot be stored. rear == maxSize - 1 [queue full]
-
problem
You can't use it after using it once.
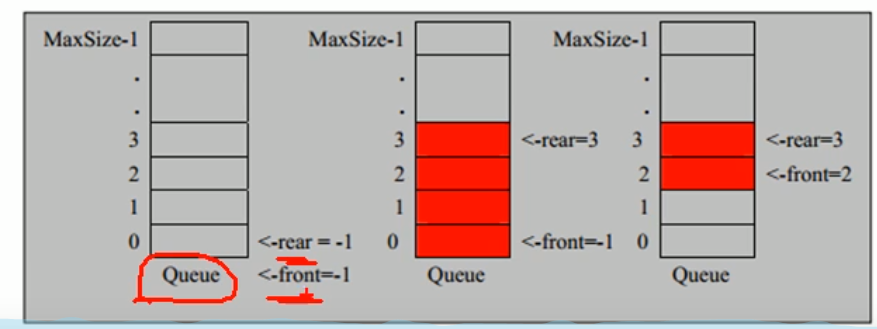
Array simulation ring queue
- Front meaning adjustment: front points to the first element of the queue, and the initial value of front is 0.
- Adjustment of the meaning of rear: rear points to the next position of the last element of the queue, because we want to make a convention. The initial value of rear is 0.
- When the queue is full, the condition is (rear + 1)% maxsize = front [Full]
- When the queue is empty, rear = front is empty
- Number of valid data in the queue = = (rear + maxsize - front)% maxsize = = rear = 1 front = 0
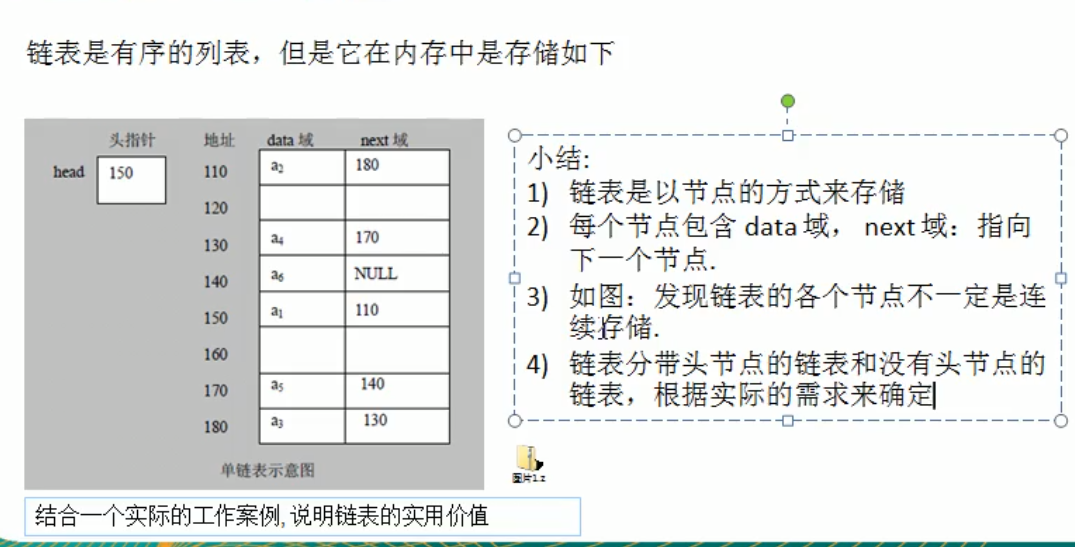
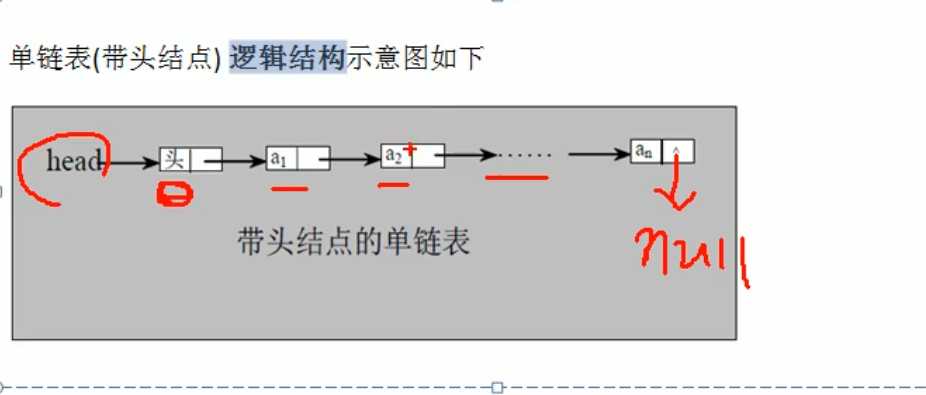
Single linked list
Schematic diagram of adding linked list
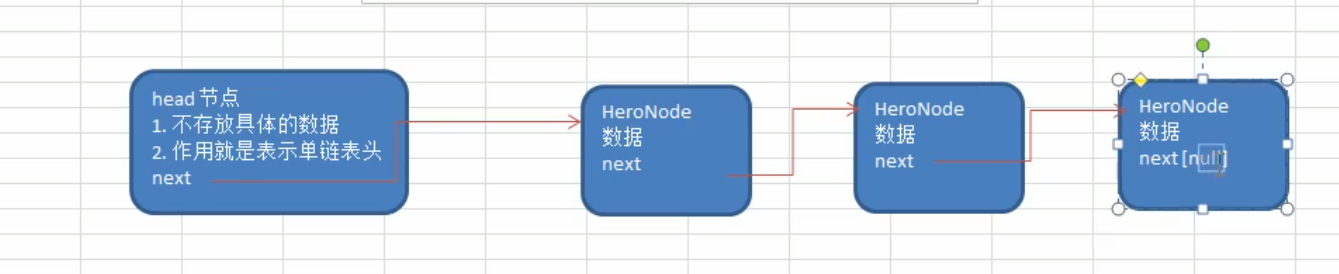
- First create a head node to represent the head of the single linked list
- After that, every time we add a node, we will directly add it to the end of the large linked list
Traversal:
- Through an auxiliary variable, it helps traverse the whole single linked list
Add a linked list by sorting a field

thinking
- First, find the location of the newly added node through auxiliary variables and traversal
- New node next = temp.next
- temp.next = new node
Modify linked list
- Find the node
- Modify the content of this node
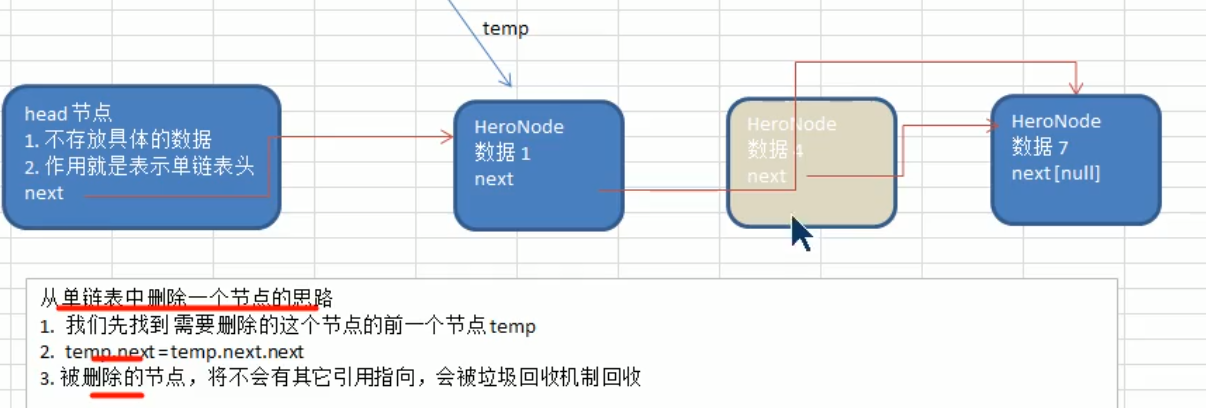
Delete node
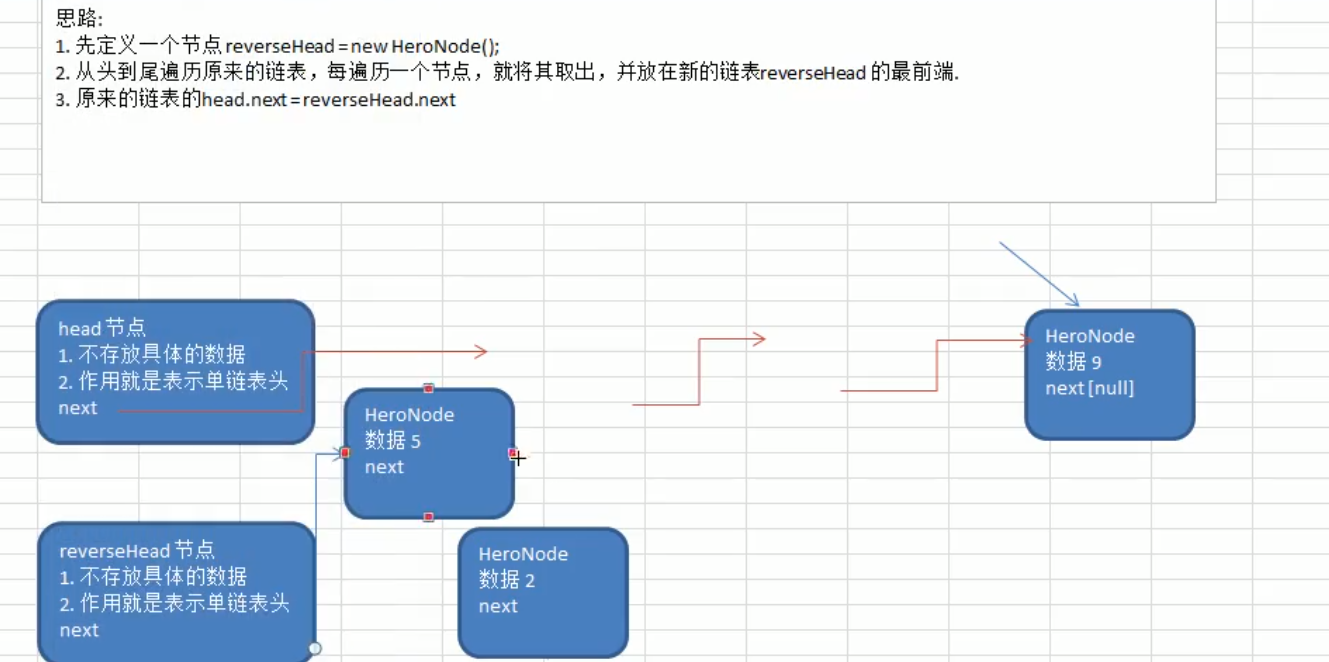
Tencent interview question - reverse linked list
Baidu interview question - print linked list from end to end
- Method 1: reverse the single linked list and then traverse it. This will destroy the structure of the original single linked list. It is not recommended
- Method 2: you can use the stack data structure to press each node into the stack, and then use the first in and last out characteristics of the stack to achieve the effect of reverse printing.
Bidirectional linked list

Traversal, addition, modification and deletion
-
ergodic
1) Traversal is the same as that of a single Necklace table, but it can be traversed in reverse order
-
add to
1) Find the last node of the bidirectional linked list
2)temp.next = newHeroNode
- newHeroNode.pre = temp
-
modify
Same as single linked list
-
delete
- Self deletion can be realized
- Directly find the node to be deleted, such as temp
- temp.pre.next = temp.next
- temp.next.pre = temp.pre
-
Sequential addition
-
Traversal linked list
-
If the added node is smaller than the next node of the current node, it means that the added node should be added after the current node, that is: ndoe no < temp. next. No also needs to consider whether this is the first node
If it is the first node, you can also operate as follows, so the condition is temp next == null || ndoe. no < temp. next. no
-
node. Pre = previous node of temp / / node = node of current pointer
-
node.next = temp.next;
-
temp.next.pre = node; // Note here that after the node is inserted, the pre of the next node of the original temp should be changed because it was previously connected to temp and should now be connected to the node. And pay attention to judge whether temp has the next node (i.e. temp.node!=null)
-
temp.next = node;
-
/**
* Sequential addition
* @param node
*/
public void addByOrder (HeroNode node) {
HeroNode temp = head;
while (temp != null) {
if (node.no == temp.no) {
System.out.println("The node already exists");
return;
}
if (temp.next == null || node.no < temp.next.no ) {
node.pre = temp;
node.next = temp.next;
if (node.next != null) {
temp.next.pre = node;
}
temp.next = node;
return;
}
temp = temp.next;
}
}
Joseph Ring problem (one-way ring linked list)


Stack
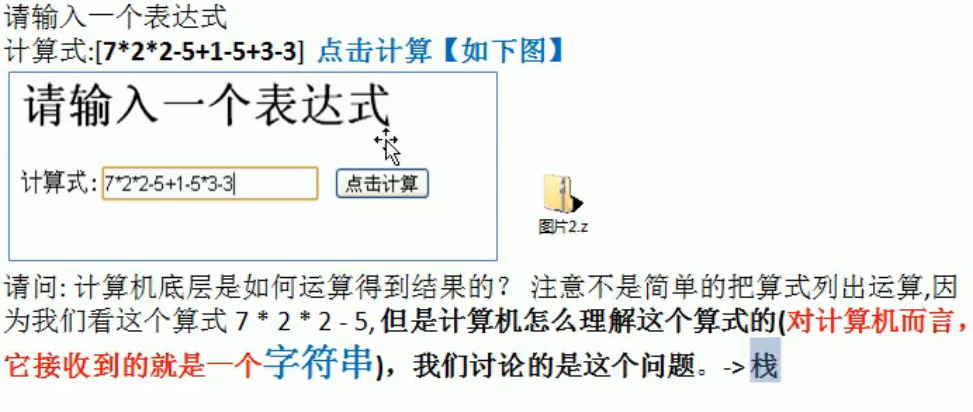
introduce
-
A stack is an ordered list of first in, then out
-
Stack is a special linear table that restricts the insertion and deletion of acid in linear table to the same end of linear table. The end that allows insertion and deletion is the changing end, which becomes the TOP of the stack, and the other end is the fixed end, which becomes the Bottom of the stack
-
According to the definition of stack, the first element to be put in the middle is at the bottom of the stack, the last element to be put in is at the top of the stack, while the deleted element is just the opposite. The last element to be put in is deleted first, and the first element to be put in is deleted last.

Array simulation stack
- Define a top to represent the top of the stack and initialize it to - 1
- When data is added to the stack, top++;stack[top] = data
- Stack out operation, int value = stack[top];top–; return value
Stack implementation integrated calculator






recursion
The concept of recursion:
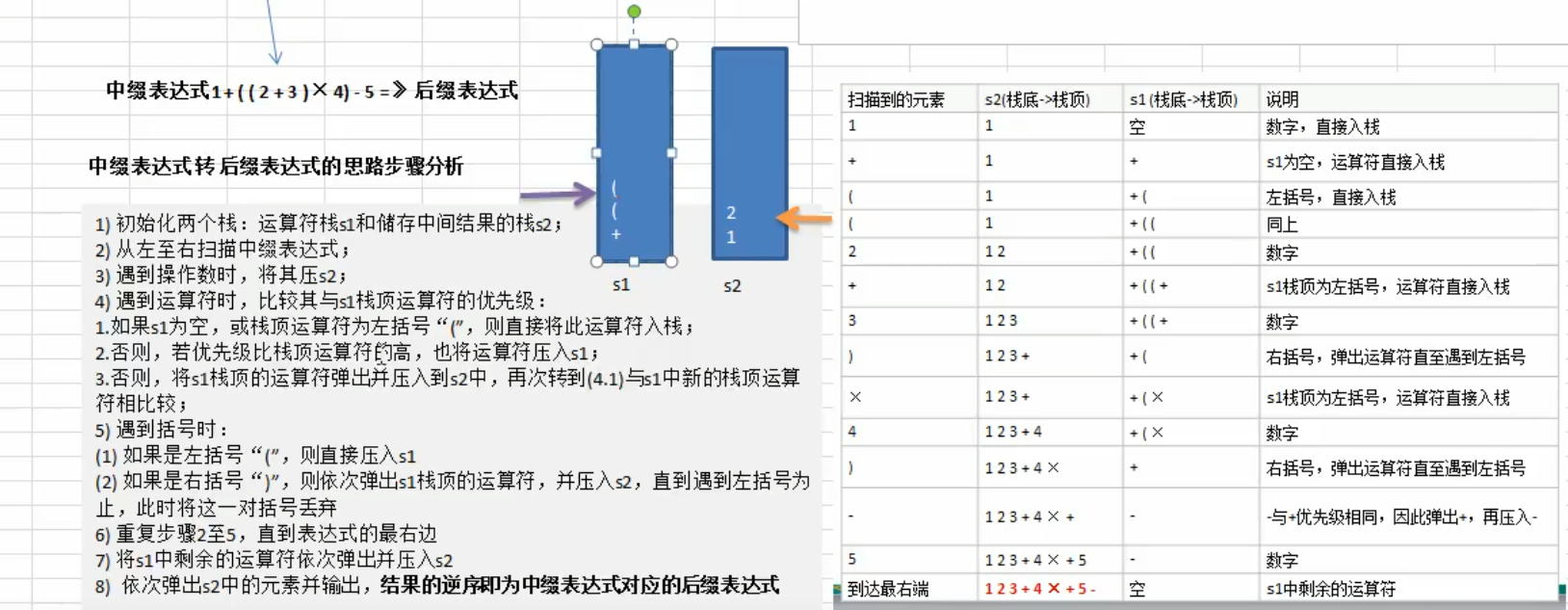
Simply put: the method calls itself, and different variables are passed in each call. Recursion helps programmers solve complex problems and make the code more concise.
Rules to follow for recursion
- When a method is executed, a new protected space is created
- The local variables of the method are independent and do not affect each other
- If a reference type variable (such as an array) is used in the method, the data of the reference type will be shared.
- Recursion must approach the condition of exiting recursion, otherwise it is infinite recursion and StackOverflowError occurs
- When a method finishes executing or encounters a return, it will return. The result will be returned to the person who calls it. At the same time, when the method finishes executing or returns, the method will also finish executing.
Recursion maze problem
/**
* @author lixiangxiang
* @description Maze problem
* @date 2021/4/23 9:23
*/
public class Maze {
public static void main(String[] args) {
//Create map
int[][] map = createMap();
showMap(map);
//Labyrinth
runMaze(map,1,1);
System.out.println("=================");
showMap(map);
}
/**
* description: Create map
*It is stipulated that 1 represents an obstacle, 0 represents a road that has not been taken, 2 represents a road that has been taken, and 3 represents a road that cannot be taken
* @author: lixiangxiang
* @return void
* @date 2021/4/23 10:53
*/
private static int[][] createMap() {
int [][] map = new int[8][7];
for (int i = 0; i < map.length; i++) {
map[i][0] = 1;
map[i][map[0].length-1] = 1;
}
for (int i = 0; i < map[0].length; i++) {
map[0][i] = 1;
map[map.length-1][i] = 1;
}
map[3][1] = 1;
map[3][2] = 1;
return map;
}
private static void showMap(int[][] map){
for (int[] row : map) {
for (int data : row) {
System.out.print(data+" ");
}
System.out.println();
}
}
/**
* description: Walking order: lower right, upper left
*
* @author: lixiangxiang
* @param map Map
* @param x x coordinate
* @param y y coordinate
* @return boolean
* @date 2021/4/23 11:06
*/
private static boolean runMaze(int[][]map,int x,int y) {
int end = map[6][5];
if( end == 2) {
return true;
}
//If the next node doesn't pass
else if (map[x][y] == 0){
//Let's assume we can go
map[x][y] = 2;
//If you go down, you can
if (runMaze(map,x+1,y)) {
return true;
}
//If you go right
else if (runMaze(map,x,y+1)) {
return true;
}
//If you go
else if (runMaze(map,x-1,y)) {
return true;
}
//If you can't go back
else {
//Mark this point and you can't go
map[x][y] = 3;
return false;
}
}
//If the next node is 1 or 2 or 3, it cannot go
else {
return false;
}
}
}
Eight queens problem
The eight queens problem is an ancient and famous problem and a typical case of backtracking algorithm. The question was put forward by international chess player Max Bethel in 1848: put eight queens on 8X8 chess so that they can't attack each other, that is, any two Queens can't be in the same row, column or slash, and ask how many kinds of placement methods there are (92).
Analysis on the algorithm of eight queens problem
- The first queen puts the first row first - column first
- The second queen is placed in the first column of the second row, and then judge whether it is OK. If it is not OK, continue to put it in the second column and the third column, and put all the columns in turn to find a suitable one
- Continue to the third queen, or the first column, the second column... Until the eighth queen can also be placed in a non conflict position, it can be regarded as finding a correct solution
- When a correct solution is obtained, when the stack goes back to the previous stack, it will start backtracking, that is, the first queen will get all the correct solutions put in the first column
- Then go back and continue to put the second queen in the second column, and then continue to cycle through step A of 1, 2.3 and 4