recursion

Function directly or indirectly calls the function itself, which is called a recursive function
Three elements of recursion:
1) The recursive algorithm must have a basic ending condition (to solve the problem of minimum scale directly);
2) The recursive algorithm must be able to change the state to the basic end condition (reducing the scale);
3) The recursive algorithm must call itself (to solve the same problem of reducing the scale);
The recursion levels supported by default in Python environment can be viewed by the following command:

import sys
print(sys.getrecursionlimit())

Recursive call example 1 -- several simple and common application solutions

For example, sum the number sequence with cycle as follows:

def listsum(alist):
    sum = 0
    for i in alist:
        sum += i
    return sum

print(listsum([1, 2, 3, 4, 5]))

You can also use recursion as follows:

def listsum2(alist):
    print(alist)
    if len(alist) == 1:
        return alist[0]
    else:
        return alist[0] + listsum2(alist[1:])

print(listsum2([1, 2, 3, 4, 5]))

For example, recursion can also be used to convert decimal system to other base systems, as follows:

def toStr(num, base):
    convertStr = "0123456789ABCDEF"
    if num < base:
        return convertStr[num]
    else:
        return toStr(num // base, base) + convertStr[num % base]

print(toStr(255, 16))

Turtle

In order to better understand recursion, this paper introduces a kind of map library, turtle
The methods and attributes involved in this article are as follows:

• Crawling has two actions: forward (n); backward (n)
• There are two actions for steering: left(a); right(a)
• Pen up(); pendown())
• Pen attribute pen size (s); pen color (c)
  For example, simply draw a square:

import turtle

t = turtle.Turtle()
t.forward(100)
turtle.done()
for i in range(4):
    t.forward(100)
        t.right(90)
turtle.done()

Draw a five pointed star as follows:

def drawFivestar():
    t = turtle.Turtle()
    t.pensize(2)
    t.pencolor('red')
    for i in range(5):
        t.forward(100)
        t.right(144)
    turtle.done()

drawFivestar()

Draw a decreasing recursive square as follows:

def drawSpiral(t, linelen):
    if linelen > 0:
        t.forward(linelen)
        t.right(90)
        drawSpiral(t, linelen - 5)

t = turtle.Turtle()
drawSpiral(t, 100)
turtle.done()

The output graph is: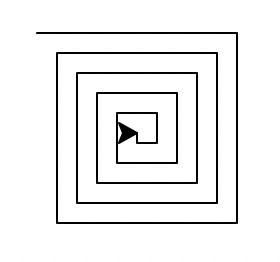

Recursive example 2--Fractal

Fractal has the feature of filling space with non integer dimension. It is a self similar recursive graph.
For example, the fractal tree code is as follows:

def tree(branchLength, t):
    if branchLength > 5:
        t.forward(branchLength)
        t.right(20)
        tree(branchLength - 15, t)
        t.left(40)
        tree(branchLength - 15, t)
        t.right(20)
        t.backward(branchLength)

def drawTree():
    t = turtle.Turtle()  #Mapping begins
    t.left(90)
    t.penup()
    t.backward(100)
    t.pendown()
    t.pencolor('green')
    t.pensize(2)
    tree(50, t)
    t.hideturtle()
    turtle.done()  # End of drawing

drawTree()

The output graph is as follows: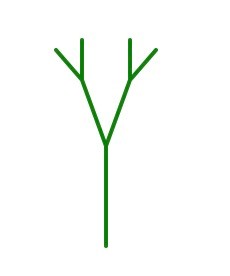

Recursive example 3 -- sherbinsky triangle or sherbinsky pyramid

In this paper, Sierpinski triangle is regarded as an equilateral triangle, which is redrawn by half of each edge, and then iterated.

def sierpinski(degree, points):
    colormap = ['blue', 'red', 'green', 'white', 'yellow', 'orange']
    drawTriangle(points, colormap[degree])
    if degree > 0:
        sierpinski(degree - 1, {'left': points['left'],
                                'top': getMid(points['left'], points['top']),
                                'right': getMid(points['left'], points['right'])
                                })
        sierpinski(degree - 1, {'left': getMid(points['left'], points['top']),
                                'top': points['top'],
                                'right': getMid(points['top'], points['right'])
                                })
        sierpinski(degree - 1, {'left': getMid(points['left'], points['right']),
                                'top': getMid(points['top'], points['right']),
                                'right': points['right']
                                })

def drawTriangle(points, color):
    # Draw equilateral triangle
    t.fillcolor(color)
    t.penup()
    t.goto(points['top'])
    t.pendown()
    t.begin_fill()
    t.goto(points['left'])
    t.goto(points['right'])
    t.goto(points['top'])
    t.end_fill()

def getMid(p1, p2):
    return ( (p1[0] + p2[0])/2, (p1[1] + p2[1])/2 )

points = { 'left': (-200,-100),
           'top': (0,200),
           'right': (200,-100) }

t=turtle.Turtle()
sierpinski(1, points)
turtle.done()

The output graph is as follows: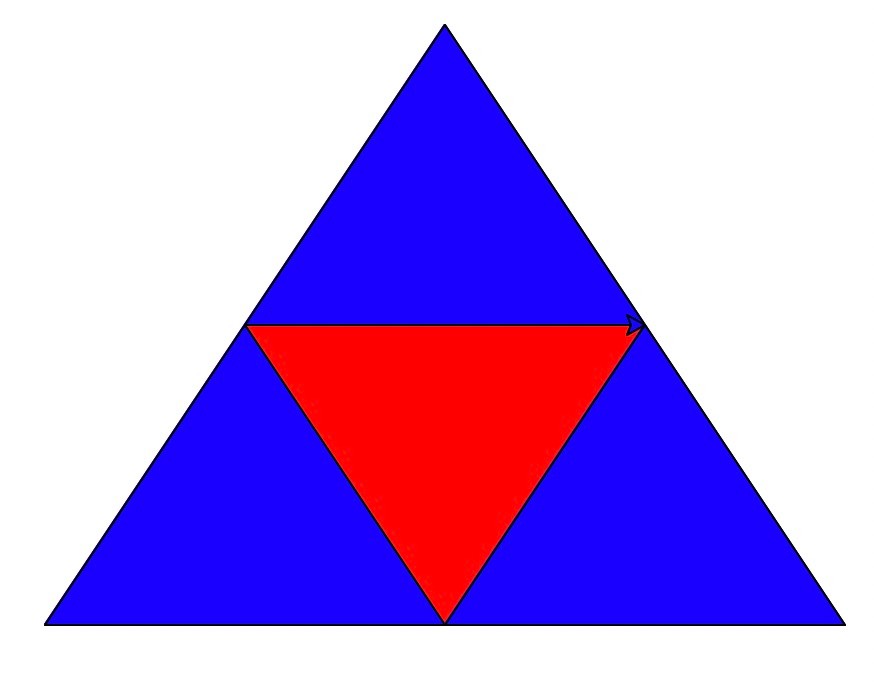

Recursive example 4 - Hanoi Tower

Hanoi Tower solution:

• Always regard the plate on the column as two, the top one and the bottom one respectively, and regard column 3 as the target column;
• The top n-1 of column 1 is regarded as a whole, moving from column 1 (start column) to column 2 (middle column) through column 3 (target column)
• Move the remaining column 1 to column 3 (target column)
• Finally, move the column 2 (middle column) as a whole through column 1 (starting column) to column 3 (target column)

def hannota(height, firstPole, secondPole, thirdPole):
    if height >= 1:
        hannota(height - 1, firstPole, thirdPole, secondPole)  # Move the top n-1 of column 1 as a whole from column 1 to column 2
        movedisk(height, firstPole, thirdPole)   # Move the last one on column 1 to column 3
        hannota(height - 1, secondPole, firstPole, thirdPole)  # Move all of column 2 as a whole from column 2 to column 3

def movedisk(disk, firstPole, thirdPole):
    print("move disk[%d] from %s to %s"%(disk, firstPole, thirdPole))

hannota(3,"Column 1","Column 2","Column 3")

The output results are as follows:

move disk[1] from Column 1 to Column 3
move disk[2] from Column 1 to Column 2
move disk[1] from Column 3 to Column 2
move disk[3] from Column 1 to Column 3
move disk[1] from Column 2 to Column 1
move disk[2] from Column 2 to Column 3
move disk[1] from Column 1 to Column 3

Recursive example 5 -- search maze game

Draw maze map; then define wall avoidance and blank; start searching (every step of searching will use the new coordinates as the origin to search recursively until the exit is found; finally, trace back the path)
As follows:

class Maze:
    #Define maze class
    def __init__(self, mazeFileName):
        rowsInMaze = 0
        columnsInMaze = 0
        self.mazelist = []
        mazeFile = open(mazeFileName, 'r')
        for line in mazeFile:
            rowList = []
            col = 0
            for ch in line[:-1]:
                rowList.append(ch)
                if ch == 'S':
                    self.startRow = rowsInMaze
                    self.startCol = col
                col = col + 1
            rowsInMaze = rowsInMaze + 1
            self.mazelist.append(rowList)
            columnsInMaze = len(rowList)

        self.rowsInMaze = rowsInMaze
        self.columnsInMaze = columnsInMaze
        self.xTranslate = -columnsInMaze/2
        self.yTranslate = rowsInMaze/2
        self.t = turtle.Turtle()
        self.t.shape('turtle')
        self.wn = turtle.Screen()
        self.wn.setworldcoordinates(-(columnsInMaze-1)/2-.5,-(rowsInMaze-1)/2-.5,(columnsInMaze-1)/2+.5,(rowsInMaze-1)/2+.5)

    def drawMaze(self):
        self.t.speed(10)
        for y in range(self.rowsInMaze):
            for x in range(self.columnsInMaze):
                if self.mazelist[y][x] == OBSTACLE:
                    self.drawCenteredBox(x+self.xTranslate,-y+self.yTranslate,'orange')
        self.t.color('black')
        self.t.fillcolor('blue')

    def drawCenteredBox(self,x,y,color):
        self.t.up()
        self.t.goto(x-.5,y-.5)
        self.t.color(color)
        self.t.fillcolor(color)
        self.t.setheading(90)
        self.t.down()
        self.t.begin_fill()
        for i in range(4):
            self.t.forward(1)
            self.t.right(90)
        self.t.end_fill()

    def moveTurtle(self,x,y):
        self.t.up()
        self.t.setheading(self.t.towards(x+self.xTranslate,-y+self.yTranslate))
        self.t.goto(x+self.xTranslate,-y+self.yTranslate)

    def dropBreadcrumb(self,color):
        self.t.dot(10,color)

    def updatePosition(self,row,col,val=None):
        if val:
            self.mazelist[row][col] = val
        self.moveTurtle(col,row)

        if val == PART_OF_PATH:
            color = 'green'
        elif val == OBSTACLE:
            color = 'red'
        elif val == TRIED:
            color = 'black'
        elif val == DEAD_END:
            color = 'red'
        else:
            color = None

        if color:
            self.dropBreadcrumb(color)

    def isExit(self,row,col):
        return (row == 0 or
                row == self.rowsInMaze-1 or
                col == 0 or
                col == self.columnsInMaze-1 )

    def __getitem__(self,idx):
        return self.mazelist[idx]

def searchFrom(maze, startRow, startColumn):

    maze.updatePosition(startRow, startColumn)
    if maze[startRow][startColumn] == OBSTACLE :
        return False

    if maze[startRow][startColumn] == TRIED or maze[startRow][startColumn] == DEAD_END:
        return False

    if maze.isExit(startRow,startColumn):
        maze.updatePosition(startRow, startColumn, PART_OF_PATH)
        return True
    maze.updatePosition(startRow, startColumn, TRIED)

    found = searchFrom(maze, startRow-1, startColumn) or \
            searchFrom(maze, startRow+1, startColumn) or \
            searchFrom(maze, startRow, startColumn-1) or \
            searchFrom(maze, startRow, startColumn+1)
    if found:
        maze.updatePosition(startRow, startColumn, PART_OF_PATH)
    else:
        maze.updatePosition(startRow, startColumn, DEAD_END)
    return found

PART_OF_PATH = 'O'
TRIED = '.'
OBSTACLE = '+'
DEAD_END = '-'
myMaze = Maze("/Users/yuanjicai/PycharmProjects/stucture/maze2.txt")
myMaze.drawMaze()
myMaze.updatePosition(myMaze.startRow, myMaze.startCol)
searchFrom(myMaze, myMaze.startRow, myMaze.startCol)

Recursion example 6 -- divide and conquer strategy and recursion to solve the problem of minimum change coins

The problem is divided into several smaller parts, and the solution of the original problem is obtained by solving each small part problem and summarizing the results. Recursion embodies the divide and conquer strategy.
Optimize the problem and find the optimal solution. For example: change the minimum number of coins.
Greedy strategy: start with the largest denomination and use as many coins as possible; when there is a balance, use the next largest denomination and use as many coins as possible; repeat until the minimum denomination
An example of recursive solution to the problem of exchange of change is given.
The solution is as follows:

• For example, first try to subtract 1 point, 5 points, 10 points and 25 points (each in the currency list) from the change;
• Recycle attempts to subtract each of the remaining change from the currency list (the number of final change coins increases by 1 for each reduction) until the change is successful; finally, compare which scheme is the best;
• The formula is as follows: numCoins=min(1 + Zero finding function (zero finding-1), 1 + Zero finding function (zero finding-5), 1 + Zero finding function (zero finding-10), 1 + Zero finding function (zero finding-25))

def recMc(coinValueList, change):
    minCoins = change  #Initialization, the worst change situation is a change
    if change in coinValueList:
        return 1    #If the change needs to match exactly one of the currencies, the return result is 1 (representing 1 coin)
    else:
        for i in [c for c in coinValueList if c <= change]:
            numCoins = 1 + recMc(coinValueList, change - i)
            if numCoins < minCoins:
                minCoins = numCoins
    return minCoins

print(recMc([1, 5, 10, 25], 7))

In the above example, recursive call consumes too much resources, because it is a complete recursion and has too many repeated calls.
In order to optimize the above example, the memory / function value cache method is used to improve the performance of recursive solution. In this method, the intermediate optimal result of the calculation process is cached in a query dictionary, and then if there is data in the query dictionary during the calculation process, the optimal result in the query dictionary is directly referenced without repeated calculation.

def recDc(coinValueList, change, knowResults):
    minCoins = change
    if change in coinValueList:
        knowResults[change] = 1
        return 1
    elif knowResults[change] > 0:
        return knowResults[change]  #Check whether the value of this call has the optimal result
    else:
        for i in [c for c in coinValueList if c <= change]:
            numCoins = 1 + recDc(coinValueList, change - i, knowResults)
            if numCoins < minCoins:
                minCoins = numCoins
                knowResults[change] = minCoins  #Record the best results of intermediate results
    return minCoins
coinCacheList = [0] * 64
print("63 The change should be:", end=' ')
print(recDc([1, 5, 10, 25, 21], 63, coinCacheList))
print(coinCacheList)

The output results are as follows:

63 cents change should be: 3
[0, 1, 0, 0, 0, 1, 2, 3, 4, 5, 
 1, 2, 3, 4, 5, 2, 3, 4, 5, 6, 
 2, 1, 2, 3, 4, 1, 2, 3, 4, 5, 
 2, 2, 3, 4, 5, 2, 3, 4, 5, 6, 
 3, 3, 2, 3, 4, 3, 2, 3, 4, 5, 
 2, 3, 3, 4, 5, 3, 3, 4, 5, 6, 
 3, 4, 4, 3]

dynamic programming algorithm

Cache the optimal solution of each step in the calculation process into a query dictionary, and then check the query dictionary in the subsequent calculation process, and try to reference the optimal solution in the query dictionary. In the process of calculation, the later the efficiency is, the higher the efficiency is.
Dynamic programming is a non recursive algorithm, its main idea is: from the simplest case to the end of a cycle of zero finding; each step depends on the optimal solution of a previous step to get the optimal solution of this step until the final result.

Dynamic programming example 1 -- the problem of minimum change

def dpMakeChange(coinValueList, change, minCoinsCacheList):
    for cents in range(1, change+1):
        coinCount = cents  # The initial assumption is that the change is all cents
        for coinType in [c for c in coinValueList if c <= cents]:  # Loop from eligible currency list
            if minCoinsCacheList[cents - coinType] + 1 < coinCount:
                # The number of change currencies is calculated according to the current currency. If it is less than coinCount, it will be temporarily stored in the corresponding location of the cache list
                coinCount = minCoinsCacheList[cents - coinType] + 1
        # Find the minimum number of zeros for each change through inner loop calculation, and store it in the corresponding location of the cache list
        minCoinsCacheList[cents] = coinCount
    return minCoinsCacheList[change]

coinCacheList = [0] * 10
print(dpMakeChange([1, 5, 10, 25], 9, coinCacheList))
print("The minimum coins are listed below:%s" % coinCacheList)

The output results are as follows:

5
 The minimum coins are listed as follows: [0, 1, 2, 3, 4, 1, 2, 3, 4, 5]

At the same time of generating the optimal solution, track the selected currency, and finally get the selected currency at each step by backtracking
As follows:

def dpMakeChange2(coinValueList, change, minCoinsCacheList, coinTypeCacheList):
    for cents in range(1, change+1):
        coinCount = cents  # The initial assumption is that the change is all cents
        bestCoinType = 1 # Initialize the most appropriate currency
        for coinType in [c for c in coinValueList if c<= cents]:  # Loop from eligible currency list
            if minCoinsCacheList[cents - coinType] + 1 < coinCount:
                # The number of change currencies is calculated according to the current currency. If it is less than coinCount, it will be temporarily stored in the corresponding location in the cache list
                coinCount = minCoinsCacheList[cents - coinType] + 1
                bestCoinType = coinType
        # Find the minimum number of zeros for each change through inner loop calculation, and store it in the corresponding location of the cache list
        minCoinsCacheList[cents] = coinCount
        coinTypeCacheList[cents] = bestCoinType  # Store the most appropriate currency in the appropriate location in the cache list
    return minCoinsCacheList[change]

def printCoins(coinTypeCacheList, change):
    coins = change
    while coins > 0:
        thisCoinType = coinTypeCacheList[coins]
        print(thisCoinType)
        coins = coins - thisCoinType

change = 16
coinValueList = [1, 5, 10, 25, 21]
minCoinsCacheList = [0] * (change+1)
coinTypeCacheList = [0] * (change+1)
print(dpMakeChange2(coinValueList, change, minCoinsCacheList, coinTypeCacheList))
printCoins(coinTypeCacheList, change)
print("The table of minimum coins is as follows%s\n The corresponding table of zero currency is as follows%s" % (minCoinsCacheList, coinTypeCacheList))

The output results are as follows:

3
 Coins to be found: 1 5 10 
The corresponding table of minimum coins is as follows [0, 1, 2, 3, 4, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 2, 3]
The corresponding table of zero coins is as follows [0, 1, 1, 1, 1, 5, 1, 1, 1, 1, 10, 1, 1, 1, 1, 5, 1]

Dynamic planning example 2: Museum robber

Problem Description: there is a treasure list in the museum, which lists n treasures and the weight and value of each. The maximum weight of the robber's backpack is W. how can the combination make the robber get the maximum benefit?
The solution of dynamic programming is to store every step in the calculation process in the cache list, so as to facilitate the use of subsequent calculation. Therefore, to solve this problem, first create a dictionary of two-dimensional table as the cache list, then calculate the optimal scheme from the "big thief backpack load" as 1, and store the optimal scheme in the cache dictionary, then gradually increase, cycle the previous step until the final result is obtained. The maximum value should be equal to:
The maximum value of the optimal solution of the current knapsack weight minus the remaining space of the current treasure weight plus the value of the current treasure (equivalent to the total value after putting the current treasure into the knapsack) compared with the optimal solution in the case of giving up the current treasure.
Solution:
Create the dictionary m {}. The Key of each element in the dictionary m is a tuple of (i,W), where W represents "the load of the robber's knapsack", i represents the first i treasures, and the corresponding value of each Key is the maximum value of the treasures under "the load of the current knapsack".
The value of m[(i,W)] should be the maximum of m[(i-1,W)] and m[(i-1,W-Wi)]+vi; the program calculates from m[(1,1)] to m[(i,W)] recursion algorithm.
If there are two babies, treasureList = [None, {'w': 2, 'v': 3}, {'w': 3, 'v': 4}, {'w': 4, 'v': 5}], the backpack load is not more than 5; the dynamic programming solution is as follows:

• When the backpack load is 1, no matter what treasure the robber sees, he can't put it into the backpack, so the maximum value is 0;
• When the weight of the backpack is 2, the robber can't put the second and third treasures into the backpack, so the maximum value is 3;
• When the backpack load is 3, the maximum value of the robber when he sees the first treasure is 3, and the maximum value when he sees the second treasure is 4, because the maximum value of m[(2-1,3)] and m[(2-1,3-3)]+4 is m[(1,0)]+4, while the maximum value of m[(1,0)] is 0, and the maximum value of M [1,3] is 3; similarly, the maximum value when he sees the third treasure is 4, and so on
• Finally, if the backpack load is 5, the maximum value when the thief sees the first treasure is 3, when he sees the second treasure is max(m[(1,5)],m[(1,5-3)]+4), so it is 7; when he sees the third treasure, the maximum value is max(m[(2,5)],m[(2,5-4)]+5), so it is 7;
  The summary formula is: maxValue = max(m[(i-1,W)],m(i-1,W-Wi)+vi)

def thief(treasureList, maxWeight):
    # Generate a two-dimensional table with n rows and m columns. The value of each cell in the table is initialized to 0
    m = {(i, w): 0 for i in range(len(treasureList))
         for w in range(maxWeight + 1)}

    for i in range(1, len(treasureList)):
        for bigW in range(1, maxWeight + 1):
            if treasureList[i]['w'] > bigW:
                m[(i, bigW)] = m[(i-1), bigW]
            else:
                m[(i, bigW)] = max(m[(i-1), bigW], m[(i-1, bigW - treasureList[i]['w'])] + treasureList[i]['v'])

    for i in range(len(treasureList)):
        for j in range(maxWeight + 1):
            print(m[(i, j)], end=' ')
        print()

    return (m[(len(treasureList) - 1, maxWeight)])

treasureList = [None, {'w': 2, 'v': 3}, {'w': 3, 'v': 4}, {'w': 4, 'v': 5}]
maxWeight = 5
print("The maximum profit value of the robber is: %d" % thief(treasureList, maxWeight))

The output results are as follows:

0 0 0 0 0 0 
0 0 3 3 3 3 
0 0 3 4 4 7 
0 0 3 4 5 7 
The maximum profit value of thieves is: 7

Modify the above content, track the ID number of the selected treasure, and the content is as follows:

def thief2(treasureList, maxWeight):
    m = {(i, w): 0 for i in range(len(treasureList))
         for w in range(maxWeight + 1)}
    choiceTreasure = {(i, w): [] for i in range(len(treasureList))
         for w in range(maxWeight + 1)}     #Store the id number of the selected treasure

    for i in range(1, len(treasureList)):
        for bigW in range(1, maxWeight + 1):
            if treasureList[i]['w'] > bigW:
                m[(i, bigW)] = m[(i-1), bigW]
                choiceTreasure[(i, bigW)] = choiceTreasure[(i - 1), bigW].copy()
            else:
                m[(i, bigW)] = max(m[(i-1), bigW], m[(i-1, bigW - treasureList[i]['w'])] + treasureList[i]['v'])
                if m[(i-1, bigW - treasureList[i]['w'])] + treasureList[i]['v'] > m[(i-1), bigW]:
                    choiceTreasure[(i, bigW)] = choiceTreasure[(i-1, bigW - treasureList[i]['w'])].copy()
                    choiceTreasure[(i, bigW)].append(i)
                else:
                    choiceTreasure[(i, bigW)] = choiceTreasure[(i - 1), bigW].copy()

    # for i in range(len(treasureList)):
    #     for j in range(maxWeight + 1):
    #         print(m[(i, j)], end=' ')
    #     print()
    #
    # for i in range(len(treasureList)):
    #     for j in range(maxWeight + 1):
    #         print(choiceTreasure[(i, j)], end=' ')
    #     print()

    return ((m[(len(treasureList) - 1, maxWeight)], choiceTreasure[(len(treasureList) - 1, maxWeight)]))

treasureList = [None, {'w': 2, 'v': 3}, {'w': 3, 'v': 4}, {'w': 4, 'v': 5}]
maxWeight = 5
bigContent = thief2(treasureList, maxWeight)
print("The maximum profit value of the robber is: %d, Treasure ID Namely: %s" % (bigContent[0],bigContent[1]))

The output results are as follows:

The maximum profit value of the robber is: 7. The treasure ID is: [1,2]

Recursive solution of Museum robbers:

def thiefRec(treasureDict, bigWeight):
    if treasureDict == set() or bigWeight == 0:
        m[(tuple(treasureDict), bigWeight)] = 0
        return 0
    elif (tuple(treasureDict), bigWeight) in m:
        return m[(tuple(treasureDict), bigWeight)]
    else:
        maxValue = 0
        for treasure in treasureDict:
            if treasure[0] <= bigWeight:
                value = thiefRec(treasureDict - {treasure}, bigWeight - treasure[0]) + treasure[1]
                maxValue = max(maxValue, value)
        m[(tuple(treasureDict), bigWeight)] = maxValue
        return maxValue
treasureDict = {(2, 3), (3, 4), (4, 5)}
maxWeight = 5
m = {}
print(thiefRec(treasureDict, maxWeight))