Clip - stack

 

Linear structure stack, very much like a magazine. As we all know, the cartridge on the clip is pressed in from the entrance and taken out from the top when used. So the first bullet pressed in will be used first. The stack is like this. When data enters, it enters from the top of the stack; It is also taken out from the top of the stack.

Stack is a variant of the sequence table, which can only be inserted or deleted from the top. Let's recall how the sequence table is defined. There are two members in the structure of the sequence table, one is the array used to store data, and the other is the Last indicating the end. Let's put the sequence table up and it's a stack. We put a new member variable in the stack to indicate the maximum capacity of the stack. So the definition of stack is on the paper.

typedef int ElementType;
typedef int Position;
typedef struct SNode * PtrToSNode;
struct SNode{
	ElementType * Data;
	// An array is defined
	Position Top;
	// Stack top pointer
	int MaxSize;
	// Maximum capacity of stack 
};
typedef PtrToSNode Stack;

By the way, I'll attach the code for creating stack space. In fact, it is very similar to creating a sequential table.

Stack CreateStack(int MaxSize){
	Stack s = (Stack)malloc(sizeof(struct SNode));
	s->Data=(ElementType *)malloc(MaxSize*sizeof(ElementType));
	s->MaxSize=MaxSize;
	s->Top=-1;
	return s;
}

According to the definition just now, the two main operations of stack are out of stack and in stack.

When entering the stack, we just need to judge whether the stack space is full, then add Top+1 and put the elements into the position of the top subscript of the array. Next, let's look at the Push function on the stack.

bool Push(Stack S, ElementType x){
	if(S->Top==S->MaxSize-1){
		printf("Stack space is full");
	}else{
		S->Top+=1;
		S->Data[S->Top]=x;
		// It can also be written as s - > data [+ + (s - > top)] = x; 
		return true;
	}
}

Out of stack is similar to in stack. You only need to judge whether the stack is empty, then obtain the elements of the array Top subscript, and finally Top -.

ElementType Pop(Stack S){
	if(S->Top==-1){
		printf("Stack is empty");
		return -1;
	}else{
		return S->Data[(S->Top)--];
	}
}

Such a simple stack is perfectly implemented. However, if implemented with an array, there will be a waste of space, so someone came up with a way to plug two stacks in one array.

Smart people must have thought that we only need to make two stack top pointers, one pointing to the place where the array subscript is - 1 and the other pointing to Maxsize. In this way, it is a stack from the beginning and a stack from the foot. Let's look at the definition.

typedef int ElementType;
typedef int Position;
typedef struct SNode * PtrToSNode;
struct SNode{
	ElementType * Data;
	// An array is defined
	Position Top1;
    Position Top2;
	int MaxSize;
	// Maximum capacity of stack 
};
typedef PtrToSNode Stack;

It is so simple, just add a new pointer to the previous definition. However, it is slightly different in judging empty and stack full. It's relatively simple to judge empty, so I'll just show you to judge whether the stack is full.

bool IsFull(Stack S){
    return(S->Top2-S->Top1==1);
}

Fat intestines are simple, right.

Then there must be a smart little cute to ask, why should we use arrays? Wouldn't using linked lists lead to a waste of space?

That's right, so let's take a look at the stack implemented with linked list.

Review the old and know the new. Let's take another look at the definition of linked list nodes:

typedef int ElementType;
typedef struct LNode * PtrToLNode;
struct LNode{
	ElementType Data;
	PtrToLNode Next;
};
typedef PtrToLNode Stack;

Next, we can define a header node. To facilitate operation, we take the header node as the top of the stack.

Stack CreateStack(){
    Stack s;
    s=(Stack)malloc(sizeof(struct LNode));
    s->Next=NULL;
    return s;
}

This stack is obviously unlimited, because we only need to add a linked list node when entering the stack. So let's study how to judge the air. Obviously, when the pointer field of the header node is empty, the stack is empty.

bool IsEmpty(Stack s){
    return(s->Next==NULL);
}

The stack operation is more intriguing. Similar to the header insertion method of linked list, we only need to allocate a new node space, fill in the data field, fill in the pointer field as the next of the header node, and finally point the next of the header node to the new node.

ElementType Pop(Stack s){
	PtrToSNode FirstCell;
	// Save the current first node 
	ElementType TopElem;
	// Save the element to return 
	if(IsEmtpy(s)){
		printf("Empty stack");
		return -1;
	}else{
		FirstCell = s->Next;
		TopElem = FirstCell->Data;
		s->Next=FirstCell->Next;
		free(FirstCell);
		return TopElem;
	}
}

Line up, eat fruit - line up

Queue, as its name implies, is a queue (laughter). If the stack is first in first out, then the queue is first in first out. Similarly, queues can also be implemented with an array of old friends. But because entering the queue needs to go in from the tail, and leaving the queue needs to go out from the head, we need two pointers, one to the head and the other to the tail. So we can get such a structure:

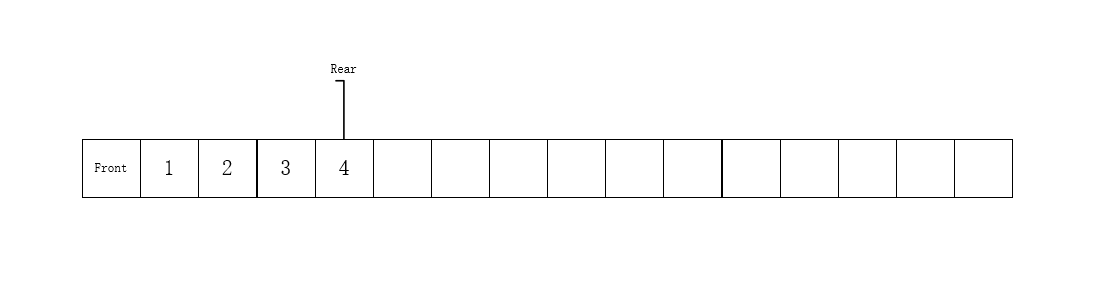
When inserting elements, we just insert them into the position of rear+1. When taking out the elements, we just need to add front+1, which is simple. But this brings a small problem.

 

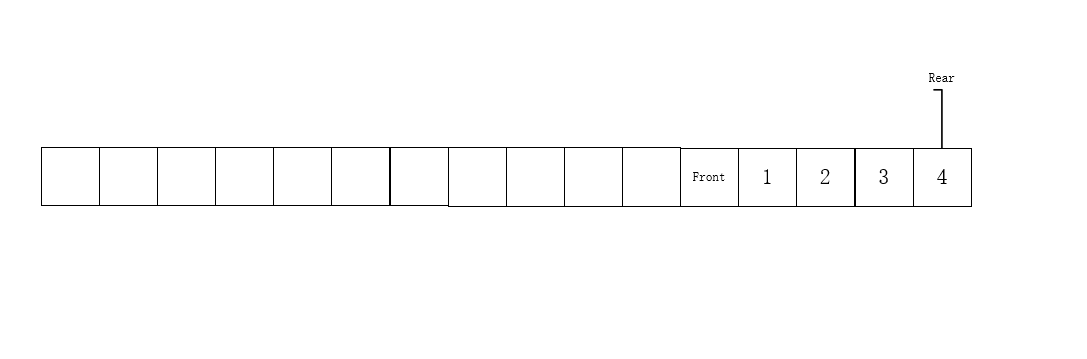
With the continuous withdrawal and addition, when the situation shown in the figure occurs, we think the queue is full, but in fact it is not. In this regard, some leaders have proposed a solution - circular queue. Circular queue is to connect an array end-to-end into a ring state, and then you can avoid the above problems.

(the drawing skills are too poor, so we don't draw anymore. You can imagine for yourself)

So let's take a look at the implementation of circular queues. We definitely need an array, two pointers, and a maximum capacity.

typedef int ElementType;
typedef int Position;
typedef struct QNode * PtrToQNode;
struct QNode{
	ElementType * Data;
	Position Front, Rear;
	int MaxSize;
};
typedef PtrToQNode Queue;

The function of creating queue is very similar to the function of creating stack:

Queue CreateQueue(int MaxSize){
	Queue q;
	q=(Queue)malloc(sizeof(struct QNode));
	q->Data=(ElementType *)malloc(MaxSize*sizeof(ElementType));
	q->Front=q->Rear=0;
	q->MaxSize=MaxSize;
	return q; 
}

For a circular queue with a length of 10, how to judge whether it is full or empty?

Judging empty space is relatively simple. We only need to judge whether front and rear are equal.

On the contrary, there may be two situations. First, if front = 0 and rear = 9, the queue is full. We can sum up a condition that is rear front = maxsize-1 But there is another case, if front=2,rear=1. Since the front node is the head node and does not store data, it should also be regarded as the queue is full, but the condition just can not be used. Let's extract the current situation and get real + 1 = front. We find that the first formula can be deformed to get (rear+1)-front=maxsize, and the second formula can become (rear+1)-front=0. Through unremitting efforts, the difference between the two formulas is only one maxsize. Next, we need to use a special operation to logically equal maxsize and 0. By making rear+1%maxsize, we can eliminate the impact of "number of turns". Because the difference between rear+1 and front is either maxsize or 0, the result of maxsize remainder for rear+1 must be equal to front. To sum up, the final full sentence formula is:

bool IsFull(Queue q){
	return((q->Rear+1)%q->MaxSize==q->Front);
}

Next, let's complete the process of adding to and removing from the queue. Because it is a circular queue, you can't just let rear + + enter the queue. If it exceeds the length of the array, it won't be fun. When we reach the end, we can also skillfully "pocket" the tail in%maxsize's way.

bool AddQ(Queue q, ElementType x){
	if(IsFull(q)){
		printf("The queue is full");
		return false;
	}else{
		q->Rear=(q->Rear+1)%q->MaxSize;
		q->Data[q->Rear]=x;
		return true;
	}
}

Similarly, when we take it out, we should also let our head "pocket" back.

ElementType DeleteQ(Queue q){
	if(q->Rear==q->Front){
		printf("The queue is empty");
		return -1;
	}else{
		q->Front=(q->Front+1)%q->MaxSize;
		return q->Data[q->Front];
	}
}

Like the stack, the queue can also be implemented with a chained storage structure. However, because the linked storage structure can only traverse from beginning to end, the head of the queue must be the head of the linked list, and the tail must also be the tail of the linked list. When entering the queue, we need to point the tail node to the queue node; When leaving the team, we just need to free the node of the head. The relevant codes are relatively simple, so the following table is not.