Search Binary Tree:

• Binary search tree is also called binary sort tree. It is either an empty tree or a binary tree with the following properties

  1. If its left subtree is not empty, the values of all nodes on the left subtree are smaller than the values of the root node

  2. If its right subtree is not empty, the value of all nodes on the right subtree is greater than the value of the root node

  3. Its left and right subtrees are also binary search trees

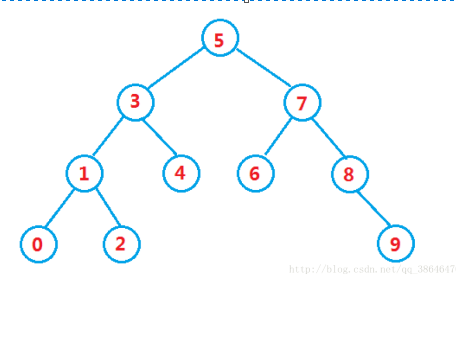
  4. For example: int a [] = {5,3,4,1,7,8,2,6,0,9};
     

Search for binary tree insertion:

int  BSTreeInsert(BSTreeNode** pptree,DataType x)
{
    BSTreeNode*parent;
    BSTreeNode*cur;
    assert(pptree);
    if(*pptree==NULL)//If it is an empty tree, create a node insertion value directly
    {
     *pptree=BSTreeBuyNode(x);
     return 0;
    }
    parent=NULL;
    cur=*pptree;
    while(cur)
    {
        if(cur->_data>x)
        {
            parent=cur;
            cur=cur->_left;
        }
        else if(cur->_data<x)
        {
            parent=cur;
            cur=cur->_right;
        }
        else
        {
            return -1;
        }


    }//Find the location to insert
    if(parent->_data<x)
    {
       parent->_right=BSTreeBuyNode(x);//If the number to be inserted is larger than the node value, insert it on the right
    }
    else
    {
        parent->_left=BSTreeBuyNode(x);
    }

    return 0;//Insert success
}

Search:

BSTreeNode*BSTreeFind(BSTreeNode* tree,DataType x)
 {
     assert(tree);
    while(tree)
    {
         if(tree->_data>x)
     {
         tree=tree->_left;
     }
     else if(tree->_data<x)
     {
         tree=tree->_right;
     }
     else
     {
         return tree;
     }
    }
    return -1;//Search failed

 }

Delete:
1. The left and right nodes to be deleted are empty;
2. The left side of the node to be deleted is empty;
3. The right side of the node to be deleted is empty;
4. Both sides are not empty.
The first case can be classified into two or three categories.

int BSTreeRemove(BSTreeNode**pptree, DataType x)
  {

    BSTreeNode *cur = *pptree;//Record the current root node with cur
    BSTreeNode *parent = *pptree;//The parent node points to the root node
    BSTreeNode *del = NULL;//Record points to delete

    while (cur)
    {
        if (cur->_data > x)//The point to be deleted is smaller than the current root node value. Go left and update the parent node at the same time
        {
            parent = cur;
            cur = cur->_left;
        }
        else if (cur->_data < x)//Ditto
        {
            parent = cur;
            cur = cur->_right;
        }
        else//Delete after finding the node
        {
            del = cur;

            if (cur->_left == NULL) //1. Left child is empty
            {
                if (parent->_left == cur)
                    parent->_left = cur->_right;
                else if (parent->_right == cur)
                    parent->_right = cur->_right;
                else if (parent == cur) //When there is no parent node
                   *pptree = parent->_right;
            }
            else if (cur->_right == NULL) //2. Right child is empty
            {
                if (parent->_left == cur)
                    parent->_left = cur->_left;
                else if (parent->_right == cur)
                    parent->_right = cur->_left;
                else if (parent == cur) //When there is no parent node
                    *pptree = parent->_left;
            }
            else//3. Left and right children are not empty
            {
                BSTreeNode *sub = cur->_right;
                while (sub->_left)
                {
                    parent = sub;
                    sub = sub->_left;
                }

                del = sub;
                cur->_data = sub->_data;//Exchange the values of the best node and the root node

                if (parent->_left == sub)
                    parent->_left = sub->_right;
                else 
                    parent->_right = sub->_right;
            }

            free(del);//Delete this node
            del = NULL;
            return 0;//Delete successful

        }
    }

    return -1;//Delete failed

  }

Insert:

int BSTreeInsertR(BSTreeNode**pptree,DataType x)//insert
  {
      assert(pptree);
      if(NULL==*pptree)//empty
      {
          *pptree=BSTreeBuyNode(x);
      }
      if((*pptree)->_data>x)
      return  BSTreeInsertR(&(*pptree)->_left,x);//(*pptree)Represents the root node pointer
          else if((*pptree)->_data<x)
       return BSTreeInsertR(&(*pptree)->_right,x);
      else
          return -1;

  }

Delete:

int BSTreeRemoveR(BSTreeNode** pptree, DataType x) //delete
  {
      BSTreeNode*cur=*pptree;
      BSTreeNode*del=cur;
      BSTreeNode*sub=NULL;
      if(NULL==*pptree)//empty
      {
          return -1;
      }
      assert(pptree);
          if(cur->_data>x)
          {
              return BSTreeRemoveR(&(cur->_left),x);
          }
          else if(cur->_data<x)
          {
              return BSTreeRemoveR(&(cur->_right),x);
          }
          else//Delete when found
          {
              del=cur;//Record points to delete
              if(cur->_left==NULL)//Left is empty
              {
                  *pptree=cur->_right;
              }
              else if(cur->_right==NULL)//Right is empty.
              {
                  *pptree=cur->_left;
              }
              else//Left and right are not empty
              {
                 sub=cur->_right;
                 while(sub->_left)
                 {
                     sub=sub->_left;
                 }
                 del=sub;
                 cur->_data=sub->_data;  
                 return BSTreeRemoveR(&(cur->_right),sub->_data);
              }
              free(del);
              del=NULL;
              return 0;

          }
     }

Search:

 BSTreeNode* BSTreeFindR(BSTreeNode* tree,DataType x)//lookup
  {
      if(NULL==tree)
          return -1;
      assert(tree);
      while(tree)
      {
       if(tree->_data>x)
          return BSTreeFindR(tree->_left,x);
        else if(tree->_data<x)
          return BSTreeFindR(tree->_right,x);
        else
          return tree;
      }
      return -1;
  }