balanced binary tree

To balance a binary tree, first of all, it is a binary sort tree,

Then, for each node's left subtree, the height difference of the right subtree (the height of the left subtree - the height of the right subtree) is at most equal to 1, and the height of the binary tree is how many layers the tree has.

The value that subtracts the depth of the left subtree from the depth of the right subtree of the nodes on the binary tree is called the balance factor BF. The value of the balance factor of all nodes can only be - 1, 0, 1. As long as the absolute value of the equilibrium factor of a node on a binary tree is greater than 1, the binary tree is unbalanced.

The closest node to the insertion node, and the absolute value of the balance factor is greater than 1, is called the minimum unbalanced subtree.

When a new node 37 is inserted, the node whose absolute value of the nearest equilibrium factor is more than 1 is 58, so 58 is the minimum unbalanced subtree.

In order to build a balanced binary tree, it is necessary to check whether the balance of the tree is damaged by the insertion node every time when the node is inserted. If it is damaged, the minimum unbalanced tree will be found and rotated to make it a new unbalanced subtree.

Balanced binary tree is to ensure its balance in the process of creating binary sort tree. Once the inserted node is unbalanced, it will rotate immediately to make it balanced.

When the equilibrium factor BF of the root node of the minimum unbalanced subtree is greater than 1, it is right-handed; when BF is less than - 1, it is left-handed;

When the BF symbol of the minimum unbalanced subtree is opposite to that of its subtree, it is necessary to rotate its subtree once to make the symbol the same, and then rotate the minimum unbalanced tree in reverse to complete the balancing operation.

According to the insertion and rotation strategy of the above binary sorting tree, a balanced binary tree can be constructed.

Now there are 10 nodes,

Int a[10] = {3, 2, 1, 4, 5, 6, 7, 10, 9, 8}

1. When inserting the first two nodes 3 and 2, they are all normal constructions. When inserting the third number 1, it is found that the BF of root node 3 becomes 2, as shown in Figure 1. At this time, the whole tree is the minimum unbalanced subtree, because BF is positive, turn it right, as shown in Figure 2. Continue inserting node 4.

   

    

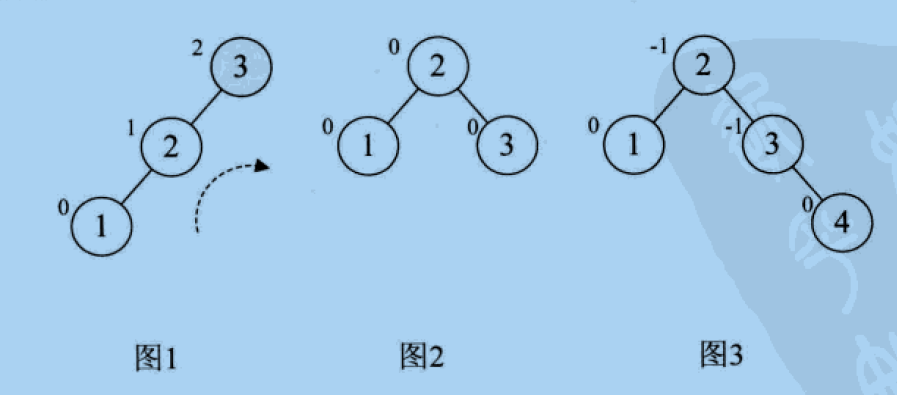
2. When node 5 is added, BF of node 3 changes to - 2, as shown in Figure 4, indicating that it is necessary to turn left, as shown in Figure 5

   

    

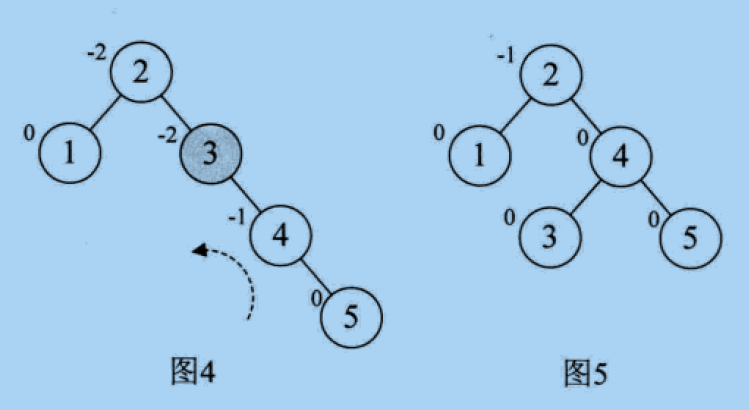
3. When node 6 is added, BF of node 2 becomes - 2, as shown in Figure 6. Therefore, it is necessary to turn left, as shown in Figure 7,
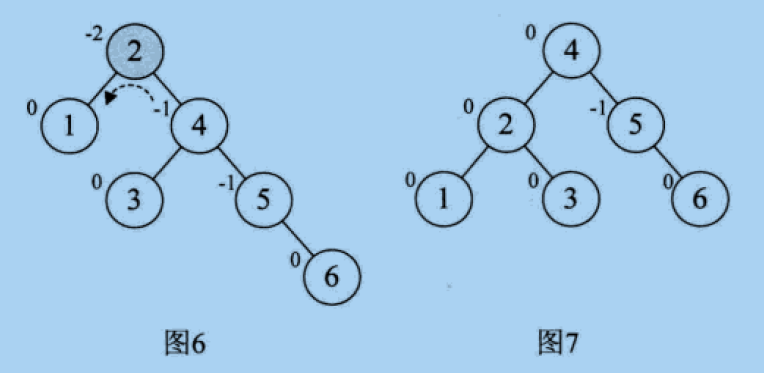
4. When adding node 7, also turn left, as shown in Figure 8 and Figure 9

   

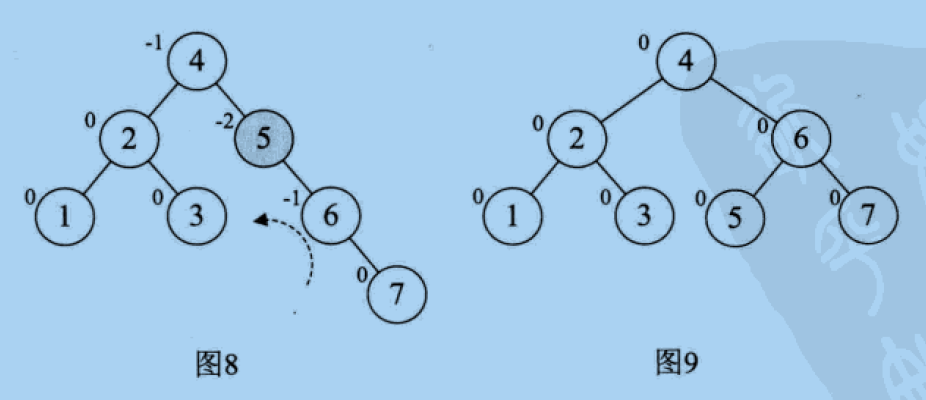
   5. Adding node 10 does not change. When adding node 9, BF of node 7 becomes - 2, as shown in Figure 11. If you rotate left 7, 9, 10 directly, because node 9 becomes the right child of 10, it does not conform to the characteristics of binary sorting tree, so you cannot simply rotate left. As we said before, if BF of the minimum unbalanced subtree is not consistent with BF symbol of its subtree, you should first select its subtree to make their BF Symbol unification, minimum unbalanced subtree in reverse rotation.

   

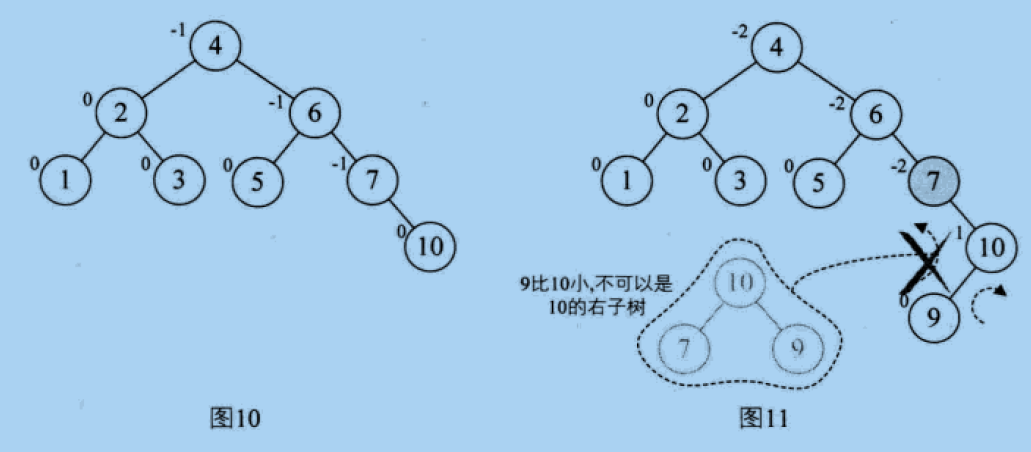
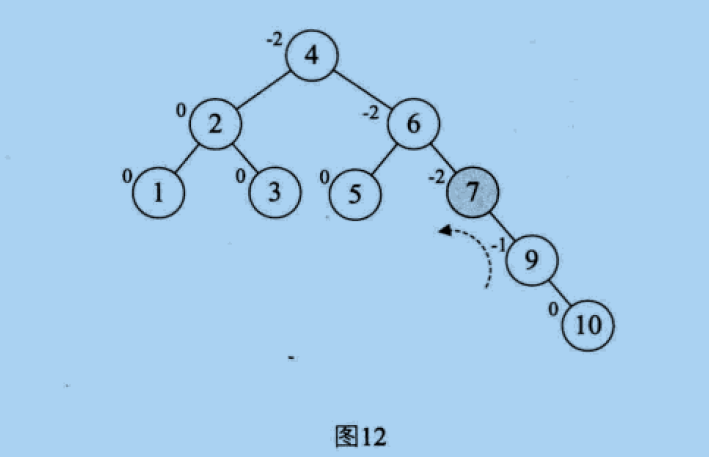
   So first, we need to do right-hand rotation on 9 and 10, and left-hand rotation on 7, 9 and 10, as shown in Figure 12 and figure 13,

   

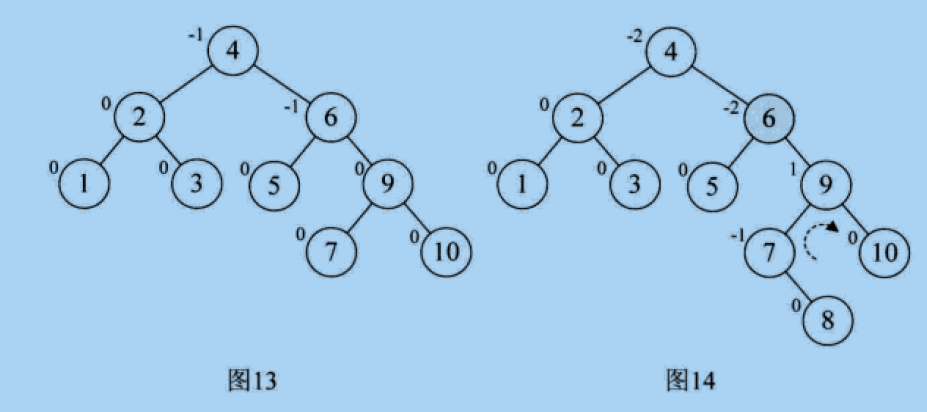
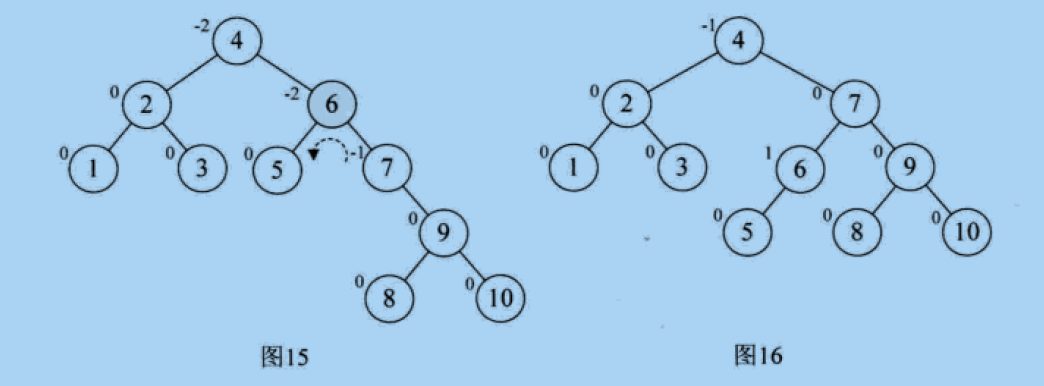
   6. At the insertion node 8, because the BF of 6 becomes - 2, the BF of its right child 9 becomes 1, as shown in Figure 14, so you need to rotate 9 to the right first, as shown in Figure 15, and rotate 6 to the left, as shown in Figure 16

   

   

   Code implementation:

   #ifndef DATA_STRUCTURE_BINARY_BF_TREE_CLASS_H
   #define DATA_STRUCTURE_BINARY_BF_TREE_CLASS_H
   
   #define OK 1
   #define ERROR 0
   #define TRUE 1
   #define FALSE 0
   #define MAXSIZE 100 / / initial allocation of storage space
   #Define max? Tree? Size 100 / / maximum node tree of binary tree
   
   typedef int Status; //State code representing the result of a function
   typedef int TreeElemType; //Data type of tree node, tentative int
   typedef TreeElemType SqBiTree[MAX_TREE_SIZE]; //Sequential storage structure array
   
   typedef struct BiTNode {
       int data;//Node value
       int bf;//Equilibrium factor
       struct BiTNode *lchild, *rchild;//Left and right child pointer
   }BiTNode, *BiTree;
   
   TreeElemType Nil = 0; //Represents an empty element
   
   Status Delete(BiTree *p);
   void R_Rotate(BiTree *p);
   void L_Rotate(BiTree *p);
   
   #endif

   #include "BinaryBFTree.h"
   
   #include "iostream"
   #include "cstdlib"
   #include "cmath"
   using namespace std;
   
   #define arrayLength(array) sizeof(array) / sizeof(array[0])
   const int array[10]={3,2,1,4,5,6,7,10,9,8};
   
   Status visit(BiTree T) {
   	if (NULL != T) {
   		cout << "value=" << T->data << endl;
   	} else {
   		cout << "T is null!" <<endl;
   	}
   	return OK;
   }
   
   void InOrderTraverseBST(BiTree T) {
   	if (NULL == T) {
   		//cout << "T is null!" <<endl;
   		return;
   	} else {
   		InOrderTraverseBST(T->lchild);
   		visit(T);
   		InOrderTraverseBST(T->rchild);
   	}
   }
   
   /*
   *The binary sorting tree with P as its heel node is rotated to the right, and P is the new root node after rotation.
   */
   void R_Rotate(BiTree *p) {
   	BiTree L;
   	L = (*p)->lchild; //The left child of p is the new root node
   	(*p)->lchild = L->rchild; //p's left child's right child, p's left child
   	L->rchild = (*p);//The new root node right child is the original p
   	*p = L;//Pointing to the new root node, the left child pointing of the left child of the original root node does not change.
   }
   
   /*
   *The binary sorting tree with p as the root is left rotated, and p is the new root node after rotation
   */
   void L_Rotate(BiTree *p) {
   	BiTree R;
   	R= (*p)->rchild;
   	(*p)->rchild = R->lchild;
   	R->lchild = (*p);
   	*p = R;
   }
   
   //The height of the subtree of the minimum unbalanced subtree.
   #define LH +1 / / left high
   #define EH 0 / / contour
   #define RH -1 / / right high
   
   /*
   * Left balanced rotation of the minimum unbalanced subtree with T as root node
   */
   void LeftBalance(BiTree *T) {
   	BiTree L, Lr;
   	L = (*T)->lchild;
   	switch(L->bf) {
   		//The new insertion node is on the left subtree of T's left child, making right rotation
   		case LH:
   			(*T)->bf = L->bf = EH;
   			R_Rotate(T);
   			break;
   		//The new insertion node is on the right subtree of T's left child, making double rotation
   		case RH:
   			Lr = L->rchild;
   			switch(Lr->bf) {
   				case LH:
   					(*T)->bf = RH;
   					L->bf = EH;
   					break;
   				case EH:
   					(*T)->bf = L->bf = EH;
   					break;
   				case RH:
   					(*T)->bf = EH;
   					L->bf = LH;
   					break;					
   			}
   			Lr->bf = EH;
   			//Turn left on T's left subtree
   			L_Rotate(&((*T)->lchild));
   			//Right turn T
   			R_Rotate(T);
   	}
   }
   
   /*
    *The minimum unbalanced subtree with T as its root node is treated by right balanced rotation,
    */
   void RightBalance(BiTree *T) {
   	BiTree R, Rl;
   	R = ( * T)->rchild; /*	R Root node of right subtree pointing to T */
   	switch (R -> bf) { /*  Check the balance of the right subtree of T and make corresponding balance treatment */
   		case RH: /*  The new node is inserted into the right subtree of the right child of T, and single left-handed processing is required */
   			( * T)->bf = R -> bf = EH;
   			L_Rotate(T);
   			break;
   		case LH: /*  The new node is inserted into the left subtree of the right child of T, and it needs to be double rotated */
   			Rl = R -> lchild; /*  Rl Right child pointing to T's left subtree root */
   			switch (Rl -> bf) { /*	Modify the balance factor of T and its right child */
   				case RH:
   					( * T)->bf = LH;
   					R -> bf = EH;
   					break;
   				case EH:
   					( * T)->bf = R -> bf = EH;
   					break;
   				case LH:
   					( * T)->bf = EH;
   					R -> bf = RH;
   					break;
   			}
   			Rl -> bf = EH;
   			R_Rotate( & ( * T)->rchild); /*  Right rotation balance of T's right subtree */
   			L_Rotate(T); /*  Left handed balance of T */
   	}
   }
   
   /*	If there is no node with the same key as e in the balanced binary sort tree T, insert a
   *  The data element is the new node of e and returns 1, otherwise 0. If the binary sort tree is caused by insertion
   *  If it is out of balance, it will be treated as balance rotation, and the boolean variable taler will reflect the length and height of T
   */
   Status InsertAVL(BiTree *T, int e, Status *taller) {
       if (! * T) { /*  Insert new node, tree "height", set teller to TRUE */
           *T = (BiTree) malloc(sizeof(BiTNode));
           ( * T)->data = e;
           ( * T)->lchild = ( * T)->rchild = NULL;
           ( * T)->bf = EH;
           *taller = TRUE;
       } else {
           if (e == ( * T)->data) { /*	If a node with the same key as e already exists in the tree, it will not be inserted */
           *taller = FALSE;
             return FALSE;
           }
           if (e < ( * T)->data) { /*	Search should continue in the left subtree of T */
               if (!InsertAVL( & ( * T)->lchild, e, taller)) /*	Not inserted */
               	return FALSE;
               if (*taller) { /*	Inserted in left subtree of T and left subtree "long height" */
   	            switch (( * T)->bf) {/*  Check the balance of T */
   	              case LH: /*  The original left subtree is higher than the right subtree, so it needs to be left balanced */
   	            	  LeftBalance(T); *taller = FALSE;
   	            	  break;
   	              case EH: /*  Originally, the height of the left and right subtrees is the same, but now the height of the left subtree increases */
   	            	  ( * T)->bf = LH; *taller = TRUE;
   	            	  break;
   	              case RH: /*  Originally, the right subtree is higher than the left subtree, and now the left and right subtrees are the same height */
   	            	  ( * T)->bf = EH; *taller = FALSE;
   	            	  break;
   	            }
               }
           }
           else { /*	Search should continue in the right subtree of T */
               if (!InsertAVL( & ( * T)->rchild, e, taller)) /*	Not inserted */
               	return FALSE;
               if (*taller) { /*  Right subtree inserted into T and right subtree "long height" */
   	            switch (( * T)->bf) {/*  Check the balance of T */
   		            case LH: /*  Originally, the left subtree is higher than the right subtree, and now the left and right subtrees are the same height */
   		              ( * T)->bf = EH; *taller = FALSE;
   		              break;
   		            case EH: /*  Originally, the height of left and right subtrees was equal, but now the height of right subtrees increased  */
   		              ( * T)->bf = RH; *taller = TRUE;
   		              break;
   		            case RH: /*  The original right subtree is higher than the left subtree, so it needs to be right balanced */
   		              RightBalance(T); *taller = FALSE;
   		              break;
   	            }
               }
           }
       }
     return TRUE;
   }
   
   int main() {
   	BiTree T = NULL;
   	Status taller;
   	for(int i=0;i<arrayLength(array);i++) {
   		InsertAVL(&T,array[i],&taller);
   	}	
   	InOrderTraverseBST(T);
   }
   

   /*output*/

   /BinaryTree$ g++ -g BinaryBFTree.cpp -o BFTree
   /BinaryTree$ ./BFTree 
   value=1
   value=2
   value=3
   value=4
   value=5
   value=6
   value=7
   value=8
   value=9
   value=10
   

   The output of traversing Figure 16 in the middle order is consistent.